Fonte: https://clubes.obmep.org.br/blog/transformacoes-geometricas/
Transformações geométricas
Table of Contents
- Introdução
- O que são transformações geométricos?
- Teoria
- Transformações isométricas
- Exercícios
- Exercícios
O que são transformações geométricos?
As transformações geométricas são transformações de figuras geométricas de imagens que podem envolver movimentos, mudança de escala, espelhamento e outras transformações que irão preservar uma característica específica.[br][br]No conjunto das transformações geométricas existe uma classe especial conhecida como isometrias que são transformações que preservam as dimensões das figuras originais, como a reflexão (Figura 1). Além disso, as isometrias assim como outras transformações também podem aparecer na natureza e em construções humanas (Figura 2)[br]
Figura 1: Reflexão de um petágono
Figura 2: Ponte Rakotzbrücke na Alemanha
Fonte: https://dicasdeberlim.com.br/alemanha/ponte-do-diabo-em-kromlau-na-alemanha/
Conheça agora um pouco mais sobre as transformações isométricas por meio deste vídeo:
Transformações isométricas
Translação
A primeira transformação isométrica que iremos estudar é translação. Como seu nome indica é o ato de mover uma figura mantendo suas devidas proporções. Algebricamente pode-se definir como uma função a que leva cada ponto P (x,y) em relação à um vetor (a,b) de uma figura à outro ponto P' (x+a, y+b).[br][br]Destaca-se que a partir dessa dessa definição, se possuirmos pontos de uma figura e o vetor diretor, para obtermos a figura transladada basta somar cada ponto da figura com as coordenadas do vetor e gerar a figura correspondente. Por exemplo: Dado o ponto A (0,2), se quisermos obter a translação desse ponto a partir do vetor diretor (1,2) obteremos o ponto A' (1,4).
Experimente o applet e perceba como as mudanças de direção, sentido e comprimento do vetor diretor afetam a figura que está sendo gerada pela translação.
Reflexão
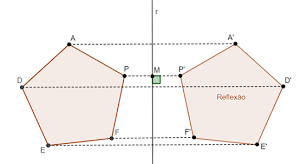
Na isometria de reflexão, uma nova figura é gerada a partir do espelhamento da figura original em relação à um eixo de simetria. É dito que as figuras são simétricas.
Maninipule o applet sabendo que o quadrilátero A'B'C'D' é a figura gerada por reflexão em relação a reta r do quadrilátero ABCD
Rotação
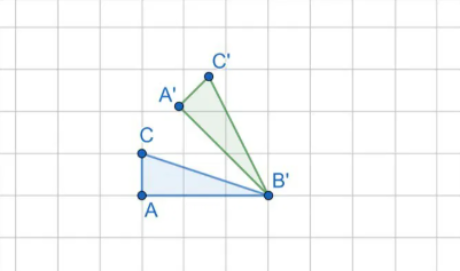
A última transformação isométrica a ser discutida é a rotação que consiste na transformação que gera uma nova figura a partir da rotação da figura original em torno de um ponto P em um determinado ângulo [math]\alpha[/math]. Por convenção, adota-se ângulos positivos para rotações no sentido horário e negativos para rotações no sentido anti-horário.
Maninipule o applet sabendo que o quadrilátero A'B'C'D'E'F' é a figura gerada por rotação em relação ao ponto K a partir da figura ABCDEF
Exercícios
Questão 1
O que é uma transformação isométrica?
Questão 2
Observe a seguinte imagem e responda à qual transformação geométrica ela se refere:
Questão 3
Dado um quadrilátero ABCD, que possui o ponto A com coordenadas (1,8). Qual será a coordenada do ponto transladado correspondente por meio de um vetor (3,4)?
Questão 4
Dado um vetor v (3,2) e um triângulo ABC, A(1, 1), B(3, 5) e C(6, 1). Escreva quais serão as coordenadas dos pontos A', B' e C' que formarão o novo triangulo transladado.