3e - Livret GeoGebra
3e - Livret Geogebra
Table of Contents
- Fractales
- Arbre de Pythagore - Partie 1 : Graphique
- Arbre de Pythagore - Partie 2 : Graphique 3D
- Triangle de Sierpinski
- Défis constructions (sans logiciel)
- Scratch (introduction)
- Scratch ★ (lignes brisées)
- Scratch ★★★★(blocs)
- Scratch ★★★(lignes brisées, boucles)
- Transformations du plan
- Image d'un point par une homothétie
- Image d'un triangle par une homothétie
- Théorème de Thalès
- Configuration "papillon"
Arbre de Pythagore - Partie 1 : Graphique
Objectif de l'activité
Déterminer la longueur optimale du côté du carré 1 pour l'arbre de Pythagore qui sera affiché en classe.
Zone de travail
1. Crée un curseur [icon]/images/ggb/toolbar/mode_slider.png[/icon] en sélectionnant les paramètres ci-dessous.
2. Crée un segment [AB] de longueur n.[br][icon]/images/ggb/toolbar/mode_segmentfixed.png[/icon] Segment de longueur donnée : Clique pour placer un point, puis saisis la longueur.
3. Construis un carré ABCD.[br][icon]/images/ggb/toolbar/mode_regularpolygon.png[/icon] Polygone régulier : Clique sur les deux premiers sommets, puis saisis le nombres de sommets du polygone.
4. Construis un triangle CDE, rectangle et isocèle en E.[br][icon]/images/ggb/toolbar/mode_midpoint.png[/icon] Milieu ou centre : Clique sur une figure pour placer son centre.[br][icon]/images/ggb/toolbar/mode_segment.png[/icon] Segment : Clique sur les deux extrémités du segment.
5. Construis les carrés de côtés respectifs [DE] et [EC].
6. Reproduis les dernières étapes pour construire un arbre de Pythagore jusqu'aux carrés 8, en réalisant essentiellement la partie ci-dessous.
7. Quelle est la hauteur de ton arbre de Pythagore pour n = 1 ?[br][icon]/images/ggb/toolbar/mode_distance.png[/icon] Distance ou longueur : Clique sur les deux extrémités d'un segment pour afficher sa mesure.
8. Quelle est la valeur maximale de n pour laquelle la hauteur de l'arbre est inférieure à la hauteur du mur de la salle de classe ?
9. Détermine l'aire totale [math]A_1[/math] de l'arbre de Pythagore jusqu'aux carrés 3 (on ne comptabilise que l'aire des carrés) lorsque n = 1.[br][icon]/images/ggb/toolbar/mode_area.png[/icon] Aire : Clique sur une figure géométrique fermée pour afficher son aire.
10. Détermine l'aire totale [math]A_{10}[/math] de l'arbre de Pythagore jusqu'aux carrés 3 (on ne comptabilise que l'aire des carrés) lorsque n = 10.
11. Par quel nombre doit-on multiplier [math]A_1[/math] pour obtenir [math]A_{10}[/math] ?
12. Compléter la formule suivante : [math]A_1\times...=A_n[/math] où [math]A_n[/math] est l'aire de l'arbre de Pythagore jusqu'aux carrés 3, et n est un nombre entier quelconque.
Scratch (introduction)
Exemple
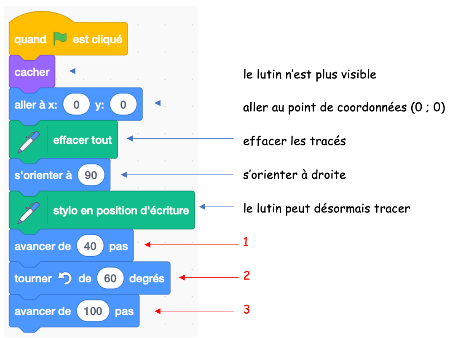
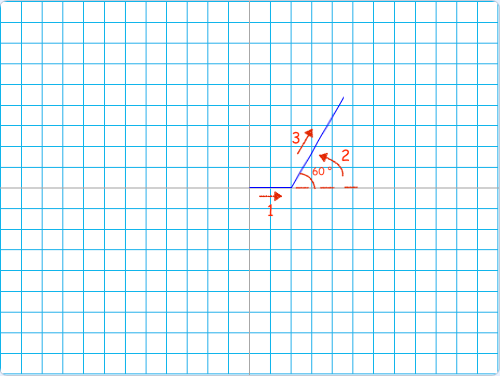
Image d'un point par une homothétie
[b]Partie A[/b] Je construis
Place un point A et un point O.[br][i]Bouton à utiliser : [icon]/images/ggb/toolbar/mode_point.png[/icon][/i]
Crée un nombre k, variant de 0 à 5.[br][i]Aide : Sélectionne le bouton curseur [icon]/images/ggb/toolbar/mode_slider.png[/icon], puis clique sur la zone graphique, et enfin, saisis 0 pour min et 5 pour max.[/i]
Positionne le curseur sur k = 2.
Construis le point A', image du point A par l'homothétie de centre O et de rapport k.[br][i]Aide : Sélectionne le bouton homothétie [icon]/images/ggb/toolbar/mode_dilatefrompoint.png[/icon], puis sélectionne le point A, puis le point O, et enfin, saisis le rapport de l'homothétie : k.[/i]
Trace la droite (AA').[br]Bouton à utiliser : [icon]/images/ggb/toolbar/mode_join.png[/icon]
[b]Partie B[/b] Je verbalise (homothétie dont le rapport est un nombre positif)
Que peux-tu dire des points O, A et A' ?
Dans la fiche de calcul du tableur, calcule (comme ci-dessous) :[br][list][*]OA' dans la cellule A1[br][/*][*]OA dans la cellule A2[/*][*]OA'/OA dans la cellule A3[/*][/list]
OA' > OA lorsque :
OA' = OA lorsque :
OA' < OA lorsque :
[b]Partie C[/b] Je verbalise (homothétie dont le rapport est un nombre relatif)
Crée un nombre k', variant de -5 à 0.
Positionne le curseur sur k' = -2.
Construis le point A'[sub]1[/sub], image du point A par l'homothétie de centre O et de rapport k'.
Fais varier les rapports k et k' des homothéties.[br]Compare les images obtenues à partir des homothéties de rapport k et k'.[br]Quel est le point commun entre l'homothétie de rapport k (positif) et l'homothétie de rapport k' (négatif) ?
Quelle est la différence entre l'homothétie de rapport k (positif) et l'homothétie de rapport k' (négatif) ?
[b]Partie D[/b] Je conjecture les étapes de construction sur papier
Sur quel élément géométrique se trouvera le point A', image du point A par une homothétie de centre O et de rapport k quelconque ?
Si k est positif, comment peut-on calculer la longueur OA' à partir de la longueur OA et du rapport k ?
Exemple : [br]On souhaite construire le point B', image d'un point B par l'homothétie de centre O et de rapport 3.[br]Calculer OB', sachant que OB = 2 cm.
Sur la zone graphique ci-dessous, construis le point B', image du point B par l'homothétie de centre O et de rapport 3.[br]Mesure la longueur OB', puis vérifie que cela correspond au résultat trouvé à la question précédente.[br]Bouton à utiliser : [icon]/images/ggb/toolbar/mode_distance.png[/icon]
Si k est négatif, comment peut-on calculer la longueur OA' à partir de la longueur OA et du rapport k ?
Exemple : [br]On souhaite construire le point C', image d'un point C par l'homothétie de centre O et de rapport -4.[br]Calculer OC', sachant que OC = 5 cm.
Sur la zone graphique ci-dessous, construis le point C', image du point C par l'homothétie de centre O et de rapport -4.[br]Mesure la longueur OC', puis vérifie que cela correspond au résultat trouvé à la question précédente.
Configuration "papillon"
[b]Partie A [/b]Je représente[br][br]1. Reproduis la figure ci-dessus dans laquelle :[br]- (AO), (BO) et (AB) sont trois droites définies par trois points non alignés A, B et O ;[br]- M est un point appartenant au segment [AO] ;[br]- (d) est la droite parallèle à la droite (AB) passant par M ;[br]- N est le point d'intersection des droites (OB) et (d).
[b]Partie B[/b] Je conjecture[br]2. Dans la fenêtre "tableur", écrire trois formules permettant de calculer les quotients [math]\frac{OM}{OA},\frac{ON}{OB}[/math]et [math]\frac{MN}{AB}[/math], en s'aidant de la capture ci-dessous.[br]
3. Déplacer le point M le long de la droite (AO), et notamment à l'extérieur du segment [AO]. [br]Que constate-t-on au niveau des valeurs des trois quotients ?
4. À partir de ce que tu as constaté ci-dessus, complète les phrases suivantes : [br]Les droites (OA) et (OB) sont ...
et les droites (MN) et (AB) sont ...
On en déduit que :