[table][br][tr][br][td][b]Factual Questions:[/b][br]]How are vertices and edges defined within the context of graph theory?[br][br]What distinguishes a simple graph from a complete graph and a weighted graph?[br][br]Explain the concepts of adjacent vertices, adjacent edges, and the degree of a vertex with examples.[br][/td][br][br][td][b]Conceptual Questions:[/b][br]How do directed graphs differ from undirected graphs, and what implications do these differences have for graph traversal?[br][br]Discuss the significance of the concepts of in-degree and out-degree in understanding directed graphs.[br][br]In what ways do trees, as a type of subgraph, uniquely contribute to the study of graph theory?[br][/td][br][br][td][b]Debatable Questions:[/b][br]Considering the constraints and definitions of Eulerian and Hamiltonian paths, which concept offers greater insight or utility in solving real-world problems?[br][br]Can the distinction between simple, complete, and weighted graphs be seen as merely theoretical, or do these distinctions have practical implications in fields like computer science and network analysis?[br][br]Is the classification of graphs into directed and undirected overly simplistic given the complexity of modern networked systems?[br][/td][br][/tr][br][/table][br]

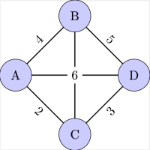
[b]Graphs[/b]: A graph is a collection of points, called vertices, which may be interconnected by lines called edges.[br][b]Vertices[/b]: Also known as nodes, these are the fundamental units from which graphs are formed.[br][b]Edges[/b]: These are the connections between vertices in a graph.[br][b]Adjacent vertices[/b]: Two vertices are adjacent if they are connected by a single edge.[br][b]Adjacent edges[/b]: Two edges are adjacent if they share a common vertex.[br][b]Degree of a vertex[/b]: This refers to the number of edges incident to (or emanating from) a vertex.[br][br]For example,

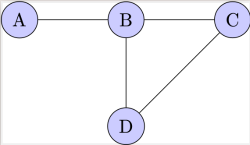
[b]Adjacent vertices[br][/b]Vertices A and B are adjacent because they are connected by a single edge.[br]Similarly, B and D are adjacent, as are C and D.[br] [br][b]Adjacent edges[br][/b]Edges A-B and B-C are adjacent because they share a common vertex, B.[br]Similarly, B-D and C-D are adjacent because they share vertex D.[br] [br] [b]Degree of a vertex[br][/b] Degree of B is 3 because there are three edges incident to B (A-B, B-C, B-D).[br] Degree of C, and D are 2, as two edges are incident to each of these vertices.

 [b]Simple Graphs[/b]: A simple graph is an unweighted, undirected graph containing no loops (edges connected at both ends to the same vertex) and no more than one edge between any two different vertices..[br]

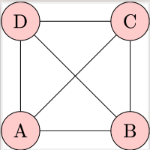
[b]Complete Graphs[/b]: A complete graph is a simple graph in which every pair of distinct vertices is connected by a unique edge. This means in a complete graph with n vertices, every vertex has an edge to every other vertex

 [b]Weighted Graphs[/b]: A weighted graph is a graph in which each edge is assigned a weight or cost. This is useful in problems where the edges have some value, like the distance between two locations on a map.

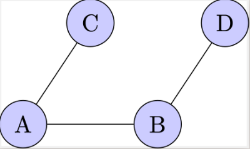
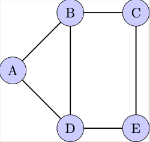
 [b]Connected[/b]: In the context of graph theory, a graph is connected if there is a path from any vertex to any other vertex in the graph. This means it's possible to get from any one vertex to any other by a sequence of edges. For example,

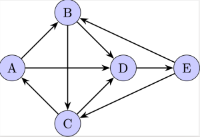
[b]Directed Graphs:[/b] These are graphs where the edges have a direction, indicated by arrows. Each edge connects an ordered pair of vertices and points from one vertex (the tail) to another (the head). Directed graphs are also known as digraphs.[br][b][br]Strongly Connected[/b]: This term applies to directed graphs. A directed graph is strongly connected if there is a directed path from any vertex to every other vertex. That means you can start at any vertex and follow the direction of the arrows to reach any other vertex.

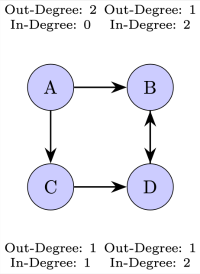
In-Degree and Out-Degree of a Directed Graph: The in-degree of a vertex is the number of edges pointing to it, while the out-degree is the number of edges that the vertex points to. In other words, in-degree counts the incoming arrows to a vertex, and out-degree counts the outgoing arrows from a vertex.[br]

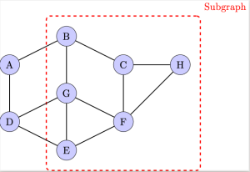
Subgraphs: A subgraph is a graph formed from a subset of the vertices and edges of another graph. It retains the connections that were present in the larger graph.[br]

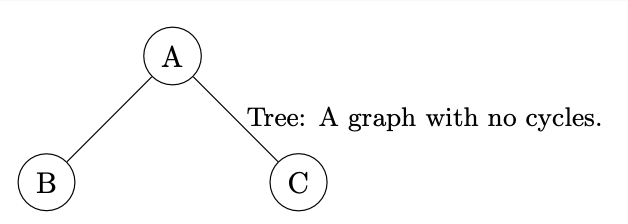
Trees: A tree is a special type of graph that is connected and has no cycles. This means there is exactly one path between any two vertices in a tree. Trees are a type of subgraph where any two vertices are connected by exactly one path.[br]

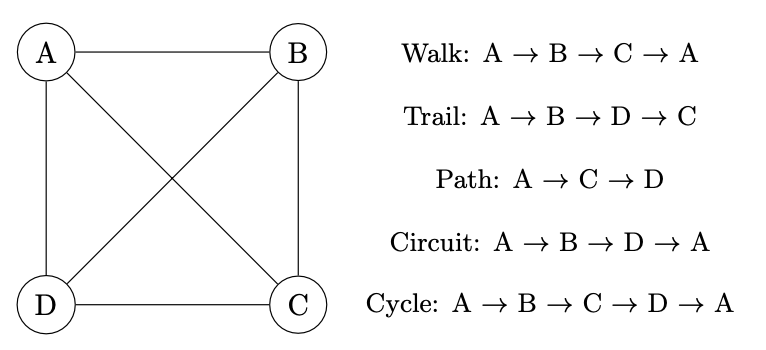
AHL 3.16[br][br]Tree and Cycle Algorithms with Undirected Graphs: This refers to algorithms that operate on undirected graphs to identify trees (graphs with no cycles) and cycles (closed paths where the first and last vertices are the same).[br][br]Walks, Trails, Paths, Circuits, Cycles: These are different ways to traverse graphs.[br][br]• Walk: A sequence of edges and vertices wherein vertices (and possibly edges) can be repeated.[br]• Trail: A walk where no edges are repeated.[br]• Path: A trail where no vertices are repeated.[br]• Circuit: A trail that starts and ends at the same vertex.[br]• Cycle: A circuit that only repeats the starting/ending vertex.[br]

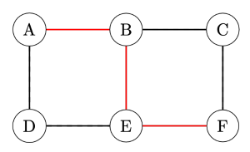
Eulerian Trails and Circuits: An Eulerian trail is a trail in a graph that visits every edge exactly once. If such a trail exists that starts and ends at the same vertex, it’s called an Eulerian circuit.

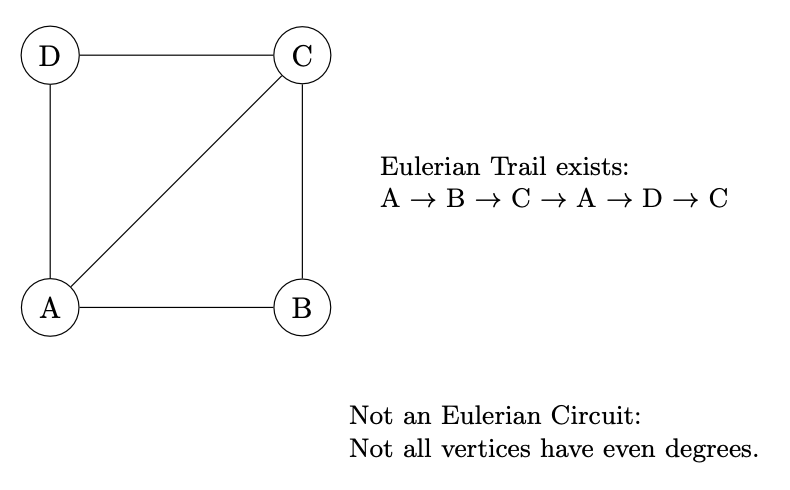
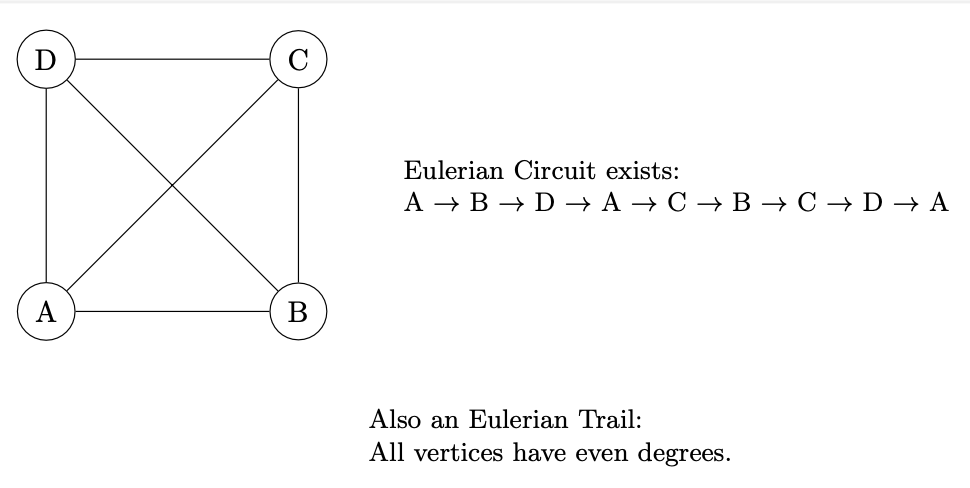
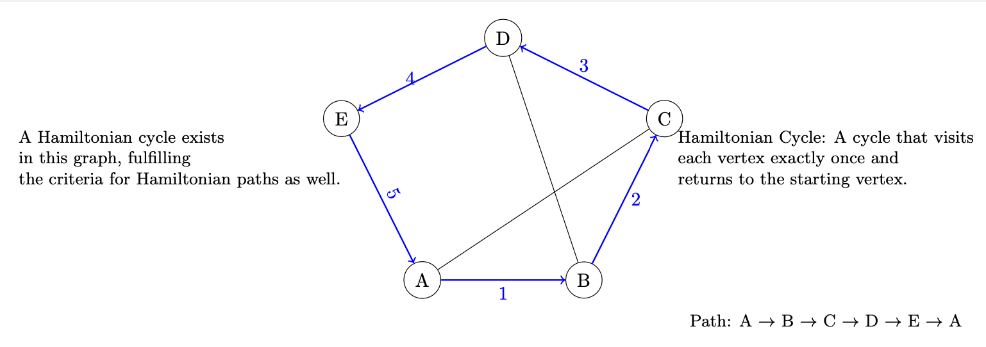
Hamiltonian Paths and Cycles: A Hamiltonian path is a path that visits each vertex in the graph exactly once; if the path is a cycle, then it’s called a Hamiltonian cycle.