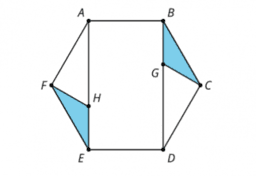
IM Geo.2.4 Lesson: Congruent Triangles, Part 2
Check your triangle to make sure the remaining measurements match.
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAsIAAAFvCAYAAABAeK10AAAgAElEQVR4AeydPXZlx5F1NSPNgj0EcgYaAc12NID2SeOztNqmTbuN9ihTdEmZLbfd+taGuNmnjjLfu3j1HnABRK6FypuZ8XPiRGTexE8Bf/g0bRgYBoaBYWAYGAaGgWFgGPiADPzhA8Y8IQ8Dw8AwMAwMA8PAMDAMDAOf5iI8RTAMDAPDwDAwDAwDw8Aw8CEZmIvwh0z7BD0MDAPDwDAwDAwDw8AwMBfhqYFhYBgYBoaBYWAYGAaGgQ/JwFyEP2TaJ+hhYBgYBoaBYWAYGAaGgbkITw0MA8PAMDAMDAPDwDAwDHxIBuYi/CHTPkEPA8PAMDAMDAPDwDAwDMxFeGpgGBgGhoFhYBgYBoaBYeBDMjAX4Q+Z9gl6GBgGhoFhYBgYBoaBYeCLL8J//vOfP/3hD394+vjLX/4yjF5g4L/+678+/fGPf/z0t7/97YLULJ2BAer6T3/606f//d//fRE41Ab7iP49t//5n//59G//9m+f4Hfa8xjg3OD8oE7gEC6nrRmQq/e+n9bRv63Zt56ro++Ko3JvK3trtNwF39Jd5/BFePWiJrFv9UD+5Zdf1hl84Cwcnq04uOhx4XurebxXuroeXvrQWu2vI7FxGXqpy/oRPNdk5iJ8jaFPT58oc07kFxa8LOTcdUvnkHiNGpWvs12E3edvMY/3qqY+a8+aq6PxHn1XHJU76vfMch/mIvxWX2he/CjKl25zEX5pxq/7s477xfTSh5YvyOe8uMH81j6Bke/X2H/Xq+EcEl4Msibf2otFJl+rRuXwOftJzI/s3eeZ20f6O5Pt3bv3rLk6yt3Rd8VRuaN+zyz31s6rm78i7AvtrW3o3WZ8iaLiEDzbV4RfIu4z+9jV8UsfWr4gn/Pifq1LxpfkU77nIrxn0YtBnq1vMddE+Fq45fA5+2mfkVm5BwO7d+9bz9XRd8VRuXtw/do22Pdv6a5z00XYl7Y/G0zfLzZl8jAnOb4I8+cv0b1ma0Uqen5FLDeZvhuTGy59qQ+2Xm99YkndFSbstJw+wKVOxtx+rmE5Eis2bOkL/z/88MMTDvDQWDcfYndNG9fyZlzKazf56lowDvlJ3cah7M6e682lOW3f+LJO0qY8yMmvv/76VGPKNC8rOytfGZtYtYnPH3/88bOfERa3MvTabX1lwGaenKNvThKLzyt/xop+2ut8gYu5n3/++anPddbUpUawyfoRTGL7aL25gLtVrnuvmXNrN/mC55SHf/NBn7lCT9/mXltgSTuXco7OCjf+0m7WVdpOHIkVn93Em3L4cJ5n9FxfcYTNS1iuxZqY8Kcv+u++++7pbLXeE5eyHZfcZW6U1XbraNf11BWfPGArm7piZC35wGausY6Nzpl6K9/6EB+9cq5hU4ysr3IlN9rRRsbjs/sCm2kXXca2lZzr7a91sQE3YO13RXOmHDZtxm48qaNv5hK/Mbuurpi1veqxpTy9HDcO1tLeJY5c0654V/WxwnSGuZsuwgA3+CSrA4IQk+aaG5reRKaMCTFB6B3ddPhDD3skhXE3ffZa4kLH+FKOCyT6NtYSO/PM7QrAOL766qvfXwjGmzwewYKfo7EmRv3BD37ELN+X+DEuZdTBBvhdX43hM7l7chwv3oy/7ZuL9CdH5kcdx5fsu0av7fTPPHbI0zfffPMkw1zHuJqT37aHLE2c13Ly008/Pb3Mf1N7ylXmjHl8pB3m8I+u7Roe5ORyhRm81L1N/J0LcDAHRjFhLzGry5x5El/a09dH7eUk87HKdfJjDt3TrFnbcr3LR+5bfacdbKGbcqyvcp6Y1LMeXLMOMudt/0j9GzO63Yzj66+/fsLOevPB3BEsz4n1aL3LL7lJHsAkdmWaG9eNexVX/xzuLlbm0758ZM70lzjBlvWAHRrxpO5v00+dtq1H17R/LVerOI/4IyeNnTn5E9e33377FJNr+lvpZgw897vCmFpuZcs86691wOOcWHkvYQs/NGJBTltya6/eLjfX9pv6z+Eo6wP8l/CJ87X6h16ESUoHDyEWQ27AJKD1GCepymIrEyvZ9LtmQlNmVYDo7/xq22JHTvmOV9lL6xnHUSxHYt3h702DLXMCTtaTV+ZSZpW35jXlk4N+Vi/9N6/YajzitC60g2w2bYF51eS711c+ldXHzvaKP32vuGON+Uu1s4rvkh/90YM3+c21jinXds9dV4zBnjnaceN8c7jDt8PwnufliPzaruV6lcfM08omtltPOXSz4d+9xvwq5ynv8wp320J2Vd/aWK037pTl2Tjwla199xjZxnIkVvG0P3F0vcsvffKKf2y4l9RvuysZbWa8/Yxe+utYe119OdDHCjeyxCl2de3bl/OXYkysK9s73rGtvxUebGlbOc6w5HnlD7vNUdoyJuXyTEfOc07czGVrXlcYzEVi3dnTdmN2ftfLifgcH+UIPfnFB+PkYuf3teYfehHu5Dg2gZBjYSQBypmELg5lWc8i77Fy2ZtQbbPmRsRPttW8RUhS/bgWjzZ3caBvHCufK4xHYkVmxa8xGG/LNQbzcS3OtIMs/DB3rSGbmyb5WOVLe+JEfieXMupl37G5lrE41z52+dzNY2dll/nOCXNis87oM5/JkxjpxZl61lfK8XwJa8riK+3xjK42cuxc5lRbxnSkLtT5aP2qZne5Tm7gNPOctXYpz6mnb3OrffxnPlnvnCub/Qp34krZnrdWsu6s/0vxYHMXR+u1T/Hk/JFY2652jAF7K1yuwxPNvav8zm7OayPz82Rs8Y+86M8x9mgZd6rr4xou1rMG00bH5lpjcD5j3Onu5rFxaQ3b1q9y1tY1XfHK4Y6zS3Kuybsx9/zKdstcw2t85k5f3Zvj1X7TxlGO4OZIPTaG1xo/9CJMUBDixlgVdhIrCSbExKWeMvSsa9vxyl7qmFBts+amyALIZ9bVy+RakMTo+iX/uziao/Tdz9g4EuslPMa7s6WuHBEn3/qhd61xOc74iWs1n/ng2Xwnj/p2zXHqrvhvuZRJXZ+1j+9s2MlYWDN2fWR8xmmfdaJd9dsu650TbYtrpcta1n/aESNzPLecmLCxwuq6/KR+Y2XcNnZ2tZf49DX9PxlY1ewq182XeuRDntGj7fLBWtZH2kj7rb/Kecr73LitY/dJ9+4N9Fijp6mX611z+qTfxZG4tdkYHOsrddJHPjc/rpkH632FizV9KY9PmjyIKfuMXz3X1RdH9ukP++5t+RBL6mjfOHacsK691OdZ+9pwfcUJa+lD/8bXfdu85I+19LnCpb+VXXWtTWQucbaSI7aOIcfmb2Vb/8pkrJdwrGJBl2adiVVOtOc4bVziCDtZn7+5OW338ItwJg0Sk0ieJToZaoJzQ6Qc+rnpdvZSZ5XQnf3UQ4ZCzeIzNovnmv+dH/SNYyeTWHi+5ss4V/x2LCtbyIgJfMjQtOu4ca3G+pOnlYwY+FklL93X/CX/O1wps/JrrTU28WDX1j4yb8pc61d20ZEjejElx/rOfLb/lQy2sWMuGx/+Lh1Y+Oj1xCr2lUzPIbuKrTF99PGqZjvXK47MP/kmR5nzS3nO+tA38tm6Di7Za73EkRhTLp9XNaKe9X/N/y6O1NNm7rPE4XPqONd98+N6x7LCxZxnHr6MERtH8q4vemNKznOdZ+PhrMUXPmxwkf6d7zi0AfZsWUs5z7PYmu8VJ8inD/0n1rbf450/bfs+X8mt5rQvXrHsOLskl7Fpd9WvbGsXGzbxrnLnWvOurtzmujrac7ySyTltws3q/Hf9bP3DL8IEDFEQyubM5O3IQsYiRb/HzJmY3PD6YW3X1MvkWQgW9koXDJ1YC1K9XTzaW9lgDT3jOIIFnSOx7vAwn/yubImD32ZA7sBuS7zOXepXnLc8XPIy4Ifx3XzKgE9+nKPP+PTRutYOsqtmnL2+4kQfrNHMf3Kz8pFzibnnzckKk74zPmwlL8qIT/s7/lg3ho5f3fbBvJwaN/21vaE9/TVG16df52SVhxVX5IKaoE6SY3nvPFtryu7kWM8cr3K+wrPCvZpLXTElVmvb+t/h1I7r1qjzjfsaFvRaR1vZ6y8xs+5885u4jA1d5NKG+imfflfP1/Dqj7PWC7h28J15dh6bnk/M9Zg57eaZpH6uy4Vruxg7DvTMv7qX+kt4sCVO5RpXyqSf5gi5FWcrOfGvajx9+IxtdZxb8WUMLavOLhbWV1janmPsZNvZZX7FSeqe6flFLsJuGgtPAiQ3501yEm6iMskUGRszddFJGf10v0qe9sC6auJCjiYmMDhnPLsC6I2tH/QzjmtY0DsSqxjTtrnIQ21ni3kOy/zNCRn7Ja6Tx+bOuLOXu+TTdeNIf8Yh98g2b+qtbGpbv2mbtRUnyrJm43mXb2WyF1P6gx/+xzR2iEs/KYMf4sg5OUiukct8y0nOJR6elUkulWkf5jLrB5kVB80NcfnyZY2mvYxL3x+1l5PMB8+XcihX1lfmxzXzbL1YZ2l3NWcNZI53OdeXvbr6ZF6Mu5yLIddX9W88yZN+5TD9sta4r2FZ6eijezHqU9vkoutdGW0QA/Fy1oI9G7rJfa7xzK/t4sOGfObU+ezlLjlmXe5TXy6NATljS31tpm765HmFTfvNSedKucTR9nNsLMk/69hlzrpRru2uYmxdY8JecrHCiv2Uka+OO2NoHda0nXrGkPbTjrGscrPSxW/GpExzJJacBxefYOUnWdpLzInvtZ9f5CJsEiy8DlqSID4LNOUkXBl0sJeJZW5XCGlLPJlo1ttHr5NE/dP71dKOq+MRI/qrA63jOILllljBjF7j2NkyXtZXjfnkg2d0kl/XdzbS7ooH192I2tOX6/aJCa7BA/+dI+XpM+/ipO9aEoMy2pCnxNYyytJrR3nw+Tt4sUVrDrFHDI2JeexYV20beerUGkwc+byKQSz4FWty6jq9/tMmz6mLDWTBLD9y33G1nY80lpOsWZ6v5VCO4HbHJ/ybS/qVXNeeNZQ5vpRzcdh3jfZ84sEurTFgAw4ab8djjcmh9vS5wy3GFZadjjazTzu5r83lDpfzHZ+2V3Hii4btxJ15Ur97/TU/ymUc2Ba/6/Ta0Dc6yF2q08yrsWqnsax47/MN37t4lQVX85e+Ui7j49k1Y6Tf6XYemjNwGLN+jD3tp8wlnRWO1NWH/SoW5TMvYDGXrqvLfLfWRad/xBG95q7tvOb48EX4S0Be2xxfYnt0n88AG2h3eDzf2n003Ex9eNzH+lgZBj4GA75Y8yX5MSI/Z5RnPddWF6xzMng7qkuXt9utjuZ7ZODhF2EOZD4TmAvOecrnbIegB9alrySch71BMgyckwEvXX4V55woPxaqM37RgXfxmb86d68K8b2y+irmvXyMnffBwMMuwhahX2Z/H3S9vSj6K0NnOwT9ROlsX6F+e5kexB+ZAff1fDL5elXAjzfxyYjNr86f5SLmJ0of5QtT3kHOwr91Mf35GHjYRZhQ+dOsHAbTXoeBPPg4/Pg424UTjN9///3rEDReh4F3wgDnbP4p7HcS1psKgwuX56z92b4Tylmbl/U3RfAzwc5F+JmEfWDxh16EPzCvE/owMAwMA8PAMDAMDAPDwMkZmIvwyRM08IaBYWAYGAaGgWFgGBgGHsPAXIQfw+tYHQaGgWFgGBgGhoFhYBg4OQNzET55ggbeMDAMDAPDwDAwDAwDw8BjGJiL8GN4HavDwDAwDAwDw8AwMAwMAydnYC7CJ0/QwBsGhoFhYBgYBoaBYWAYeAwDcxF+DK9jdRgYBoaBYWAYGAaGgWHg5AzMRfjkCRp4w8AwMAwMA8PAMDAMDAOPYWAuwo/hdawOA8PAMDAMDAPDwDAwDJycgbkInzxBA28YGAaGgWFgGBgGhoFh4DEMzEX4MbyO1WFgGBgGhoFhYBgYBoaBkzMwF+GTJ2jgDQPDwDAwDAwDw8AwMAw8hoG5CD+G17E6DAwDw8AwMAwMA8PAMHByBuYifPIEDbxhYBgYBoaBYWAYGAaGgccwMBfhx/A6VoeBYWAYGAaGgWFgGBgGTs7AXIRPnqCBNwwMA8PAMDAMDAPDwDDwGAbmIvwYXsfqMDAMDAPDwDAwDAwDw8DJGZiL8MkTNPCGgWFgGBgGhoFhYBgYBh7DwFyEH8PrWB0GhoFhYBgYBoaBYWAYODkDcxE+eYIG3jAwDAwDw8AwMAwMA8PAYxiYi/BjeB2rw8AwMAwMA8PAMDAMDAMnZ2AuwidP0MAbBoaBYWAYGAaGgWFgGHgMA3MRfgyvY3UYGAaGgWFgGBgGhoFh4OQMzEX45AkaeMPAMDAMDAPDwDAwDAwDj2HgXVyE/+u//uvTH//4x09/+9vfHsNSWf3f//3fT3/6058+/fnPf66V8w7FDG6ejzY4hVs4PlOD+z/84Q9PH3/5y1/OBG2wfDAGqL+XPH9ek17PkZc8+176fL8Hvx+pJm7h63/+538+/du//durvUNv9f/IWnzE3nok3lvyfladh12ELbRbXhAWhBcd+rTDIcOcl7NHJxs8xGMT30u+DPR9ay/maxfhX3755TMXj7oIWx/X8HwG5rcBvHOIZk5WcmeZ29XPW4rhLFyeEcdrX3rc23kmPocnzs88a3n2bHONGGn6cv05fo7K9hn06PP9KK7nyL12TTwH62vIev4/so4uxXXU/y216B557vmu3j05ec29A8fE9BbaQy7CHp4cqHmBPUKIBdoXpCzIl7wIrwrpEQV7hJsvkRFz86pN13sTnu0ibH00TuM4W3+pfp57UJ4ttsHzTwZe89Lj/vQiS709p/VZii5nAfuM5lmOnGucIY/Yf+5tfT05/A3Dc98j6r5W/5o18VoxP8evuX5EHR3Bcc2/67fUou/S557v6t2Tk9X75wg/XyoDb8+N/0t9fon+3S/CmcxbDoNbEneLzlHSVrYzxqN2XltOzGe5CN/Kx+6AutXeo/VW9fNon2P/ZRm45Zy7F0JemuzpH3/88bPvkh2x75nwnBfvLTpHsCCz29tvcQ+9Zk0c5fs15cz1c2rvnniv+XedPGZ7ZC0+Ym89Em/y0s/w9qEvwknILYfBEZ1Obo/FwCbzKyX9FQUTpa5yuTFT33X0smB9XiUdWfTwkU0d7LOGzM5v43aDiqd19aNd5XhR8sJcXYT7q0roGI9r2DMe1ld2jEuf2hBT9soat3HhI3nP+Dsm/KiP7dTrNdaxDaaff/75qef573//+1Ms6GZ8YhenMSGTrX2qt8KDDfXRaw7lWl8ZO/aOcJTY8rnjSCy32pYv8pLNOIjR1jzlGjLY6HiZR05OM359y6d+sm+f8i0+eb7ERfsRg7r4QGaFPbE8+tm90bm45NdYOhepI1fatY5aR//yknnRD3OZk+Ss9bFjvlhT1nyIR6zibFyso0MN5b4HE009cbd+4kXGWtQvvfGlDXyKOWXlb2WnY2tsbU9bjVk97NEuxZ/YeFbXWOjl+hoXl/wYG/aIA5tw0NjF05yil7IZe9pOvNqiT5lr/sGGnfxY1WLykdjwx1ido1hTTuxiWdWLfhJny6Fv3STelsOW/tMevGXLuJw3V6ytbGAPHGdud/+KcAYLiSYh5y89uxFXiVIvk8tcj02GhYhMY0GHBCU+fWfy2za2tE/iaSs9ZRLDk/Bv/1hQxAmOLKLUadz4+umnn343tfJtbBkH9vGTtn83sojJNe1//fXXTxwyn4Wv3GoOn7s8yg8yNMdyod22oZ+MTd30Je6MF16QYQ4/ystNY/nmm2+eZLFFwyd62KHh94cffnh6dozt9pk1pjC+Wg7bGZe40p/YxYo9no1F+9nL2cqfduTwGv9pV520yzoxGLMyiW+XG3XSR8amrW+//fbJfvOlnnLp0zV69o85Zex+aZ7bzyUeV9jT56OfO4aj/uB3xyM2zFVzY90gk/lOHWvZfFyrLflVzxjwLb/aulRz6tmjTy24d6yL5kz/xoava/tbncSjXTGLw15OM86OSxspY65Yo6kj3p195FfxK2+/8unaES52foiB3Dfurgd90cPRtfecfCT3+Greb/FvXpN/cBED9r/66qvf41nlE2yJ6wjWzqd2O7/ydDQnjVc/7gPsGW9ith7Sf8eVuikHb2lfzGftT3cRhigLgI3SRc26xYjcarzaDCbfZJlk+mysZwLbF7Jty3EWkTG0fX3hpw+CI7jVzx5b+ragjVM555Vz3t4YWs84+kBorOglb9jVZ+uy1v4cN772v7LZWIypc+y4ca6wK5vY9d0c6Y8evazZHiuLDWPd2W1Oeqyt5sh5+1V8rCVvt9pOG9jUjhz1upjkl552iSfzpW32TeZFm/Y7n653r10xO24/Ox6Zz5y3/ZcYN5/P8Ql+Yu3zCBvWlnmSG7lyvfPBuPNmvYutdd0Hbatro/PbmLRvLzfiYV5fxpGyl3LZWNBPu9phfmdHvMmHXGB/h631HHcM2pLHVfzitN/5dH3VNxcrP41FO843dtdXPbLJGePmvuPQj1xo1/mdf+20njHSZ2sst2DNfOo/401/u+ddTjqOjr/xax+9rOOOCzmxsmZDr3Pj2hn7U16EJcpk9QG9Sva1ZGEzk9g29NkJXMllwaZeYmg7ytmvCi/xKUff8/r35UVv0ckZuLOps9tYruMr285e8rLT3c1jv9d6LAY3GXzSesxc89O6xgRmuGpuVvqruHcYwZa5SB/Jk7ga88qXsti2rnb+V5yov9NhXb/42Mldst02cizHK26R027mxjhZt7FubYtxV8PoKKNd7XSv/8ybdrXh+JrdzFH7eanxrraf4x/O4CPzYI2YT7mR311953zriMkcwB+tx8qlLebEpJ5jMapnz3zuybTROitb+Mk60dYuLuxfq4leZ2ydrzAYS+rt/KuPLG0Vv/bskcm8O989NldcILfys7Nrrq2j9sPY+NKfHLGObu7R1NHurf7FJ4fi29lD7hK2I1iNF9mVvBi6v5aTVV71BX//+Mc/nniUs7TftbTCJVep33ykzTM+n/oiLGEmmiKkdTHm2ATn5slnN07q6Ie+E7iS00cm3mJAf7WePnjuglInseZz4mY+ffPsJgQv6/TZtK+dXOPZ9bTLvBuh7SUvxp5487ltrvzt/GsbXmk9Vm8Vl7L6T8xPxn77h/XWX8XdvrQv95jDR/J/xGfrJDbi9iDTv/EoJw45cp7etdZhzRgv1az6K9v6Sf6Qkw/xNrcrXJd4anurWMQi3ksyYCRHxtQ4HaeNS3axY47E8dL9pRp6DhbjNGfWCPZpzY1c5n73WU5aRzz6Mg89Vm5VG7uaUyf7lb58ibV71sVj/WFTvVzPOtHvtZrQNnLNT/rQnn3abT1lzJm8Ys9cKNN92u01xuLdcYHMys/OrvZW3GmLnOQ6z+mfsXUq5ubkVv/ik0Ptr2JkDblL2I5gFbu1eC1nYky/XTs7vGAWE/9PBhuMu3UtqQNWmzhSv/lQ9qz9m7gIN9Gd3BxbTJmUFfmpk+udwJXczodFws828TNEFNGuKWtB7WymvjK9+bHlZrBwwZ1tp6uM683bzl7yYn760ND2qm9/PVanbfcYueaydY0pMSuz01/FLUb5J94+rPDBQSb/R3yufIkvfejfeJRZceLaTod1/eJjJ3fJtj6MkbqHm6yDe+TG2t5hFAf9NRnjSQ7VMa+OVzI5p9/MkXMv3XfdfYn/jMcasZ6bG2TNz85n6yhnLqyXHitnfYHF5tyq5pSxV3aln3PK2ycPzmHL/b2LC9mVrjbs3Rv9vmjOlW+7O//qy+sq/rTJ8zWZVTzJxc7Gzq65Xu0n43I/ihXZrDX5Q96mrnZv8Y8t8cmh9nf2kLuE7QhWsRP3r7/++mSvORAH/a05QTd9zVeEP316Exfhaxu7i7OLMovH59ZxvnVXchaRm01dcHIB5j/ZXCpg5Fcbo31r137nF1tuQjdwY3N+h2tnW+7hIVvzsoon5fu5/fVYeXHDDa3HzLHWF1LmwehLy/FKboV9FbcY5XCVr1t8GlPnrP05bjn15YhYsyFvfeR88narbeypS933J4DpI32veMpcpV2x66fjT7s87+JlbcWVds2r4/azs8v8qq4a1yPHzeeX+Mo4ex80N72+8ts6ynQueqwcsTW/2lzVnHr2K/2dL3Xoj+zv5Cp1j9QE3K3eF2LDRjZj7jp1rKy14Hmwil9Ze/OojvP2R7hY+dnZdb5jxJ9x9hpjzwLkGHfsraufjsv59mG85qD1VjGi0/w0th6v4txh32Fsn9g09/Q57jiM33l8JLdPyot360pOW4lzhU2bZ+xf5SIMYf3Skxz+ly7E2iyOTFIXY48t4t4k2qRvHdc6gSbZgkFOTJn4nCe2lNd29ug2viO40Usu8IO/1ZybAb/o8Zsf2mdjSjusGX/aYr75U645Sfv53Bz2WFk5kc8eI6duYl/hacz6WOVC/YxbP3LIWtaxOqs58e98aivlwJUXAP03xytO9EPvuriZa3+32taPdZg+WNPutdysMGpTXW11/GKw15Z6zieexIk9cubczo/5Tf/wyGXGTwAu+U4c9342n/TZ5DDrynWwfv/99w6feu0ob8zaXXEDH1mnnxmMGkjekJErfWnbPGgH3yv7xtby6tlf0zc25e2ZX+3l1VzGhl7WhPa6N17syYEy+s75Fc9yYAxymjZZW/GnL3ttpU/XxKMf6yK52Plp3MTtJzDJm77omc/9K7acQ6ZzL6dpl+eM/4h/7bT9XYzgu4TtCFZ9JnbjlvfkiLnkf5cTZDp+4kq81k3Gq/2sh54TMz4St3L0b6Gd6iKcpEKsH5kcSIXcTGyPJZ7EaMPexOx0uqCxZTFiAz1xZuL1udJ3LXt0Oy7XL+HWt/Fgg98RnEWNHXAqQw8uPnY+0XEzIK+cm0vexLjir7FhJ/OkLr2ycthjZcUEdlqPlaNv3tRRZoVZPeNVdhW3GFMWH/JMrPggF8lXyji/yr8+tdc51b+cifUSJ8qoq216sSDj+i220Rd72pp1MfYAACAASURBVNQ3/bXcpA0xogN38rDDmH58VlZb9OZNvlzTj+vqNhfYbl108lvbrotZPI/u4Z14mn9rj76bOvJgnzY6rztuVrbkb6cjV4lNf2BRH9urc0TZxNsxMt7ps6YNY6e3DliXP+Z3+9s4tNE1scLkHPZ3tdLYdnLwpO/EKK+X4heHPbLaspffa1xc8pO62EUW3OZY//bWjBjgtN9z6Gau0FWv7T7XP7aSf+3tYsR+5qex9XiFdYXdOXjAR7eMK3OfOQOXuJNPbGdLX8ppJ+XSJ3L+jQI5UpYx66u9q8xZ+odehM8S5Evh8EBcFexLYRg/w8BrMLA66F8Dx/j8OAy89Zqb98XHqdWJ9NwMzEX4Tvnxs6n8rPBOpsfMMHBqBvwKweqrB6cGPuDeLANvvebmffFmS2+Av0MG5iJ8h6RyAXgr3wK4Q7hjYhh4YsCvaFH7812QKYqXYOA91Ny8L16iUsbHMHCcgbkIH+dqK8nh3P/pZCs8C8PAO2KAuqf+pw0DL8XAW6+5eV+8VKWMn2HgGANzET7G00gNA8PAMDAMDAPDwDAwDLwzBuYi/M4SOuEMA8PAMDAMDAPDwDAwDBxjYC7Cx3gaqWFgGBgGhoFhYBgYBoaBd8bAXITfWUInnGFgGBgGhoFhYBgYBoaBYwzMRfgYTyM1DAwDw8AwMAwMA8PAMPDOGJiL8DtL6IQzDAwDw8AwMAwMA8PAMHCMgbkIH+NppIaBYWAYGAaGgWFgGBgG3hkD7/YizC8tfwt/4/qd1dMpwvGvNvXfPj8FuFcA4d985w9f8PGnP/3pExy9dPvb3/72tCfBMH+B8aXZv4+/t7a3svbnj77cpwbeqxX/WMu8Nx6XYd8BZ/srpHe/CHtQ+tL9khevpN1yoZ2L8PFi5gB4jYuRCDl4+PAgIneMV5cla2J1WKnz97///emyt5LR53N6uAHb2dvqz87Kifi/NJaVjyO8mLe3dBn55ZdfPgvt1tg/M/LGB57vL7W3OAt4h9xSN137Z6e+96bn4Wt94np2vu6NT76v1XafC/fG8Z7swSl1bfM98O4vwhxYWUgW1y2bGVvffPPN08dzD8K5CFt6l3t4XV04L2vdb5WN8dVXX32iB4t14guwNwwy33777dNHbrB8QefzlyJ9S3UEN1wa5My9x/y9Wvs4ahe9Wz6hPWr/nnK7+rk19ntie21bO25uwXVkbyFzy0XY2s930S0YX0pnxYUxeCa+FJaP6ke+dzXj+j3P0/fMNTz13eLDXIRXiV1t8pVcznngQiaF+dzD4Baf6f+jPK+K9SVjxz+55ZChZ0xzwzgWE7Xw3Xff/X55dl558m7t7A40dY70b7mOkpMjsT5S5rXr7Dmx3bN+nuP3Lcjek5tH7q23dml5JBdvoa7OgNGa2b03XO930hmwnxHD6sw/0zspObv7j0akcZ/Z5PmVKucv9UnYpUOCosW2HxZp63iAr766gM4KnxjcGGmj/RkLsn1pdwNpxzF+9S1u7dAzx2dUP//881Ovz91nWa7Tp72Vv//3//7fE87U4RneUj753X1F75JMx5DY9YN+14hcyxl8IM93CH766acn7OjYeNZ26ppDYmv8+k8O0l/GpUzyqm965pWh1w648CtmZRqLttLnERnsWW/6IubGo1/7jqPl5VJc9unDuJF1XvvGby6cp8+4Mj+9hn3typ+6ztPjX/vGxbxzHUvHqk38NR5sqK9PZLJlzpA3dmXwd4kj5V66B6ex6dv45dF5ZfPHjpQl5uQQnXvtLX3AfdoFX/Ke/jP31kDmJPU6X9YrMtrh2Xjar3vPdf2JNzG71j4bD+v4SSxPwf/2j5xoL2NHBN/M0ZNf5cSatnjWT9cCa+BA33iU1SY9MjbXiSmbmFM215k/uke0JYb2hV3wut4Y9WtsrCdfR+yhk3w2ps6JPu27XrCXfpPHxImcudBW+4ZH92liRF5e0oa+UhYs+OKjYzFX3ku6brSnvj0+xcpzxpW+javttB/l7tG/2EW4ybwGXrIpGIuGuWyM0y5ykEeD6FwjsTlOOxLeyUj7YkgZfJDkLGCeUwY/6iqnP77FDyZsdGzGkEXEnLpZFFwSKDCbuOhTZ+UPv2kr5VexpaxYMt7kDFtgQAcZ7KX+E7gL/2ArbRMjMeAXLpOz5F1c/MiF8rhBJv1jD+5sbtK0C/5d3ai34puc07TZOQZL2hVzxttcKpMxiIG+seqbeZtzGWNjUXbVtw9jz1hWPvDXuNVtLHAlZmyZR+b1ow/HYNUe8fBBc+8lrz/88MPv5wQyyCY2edbGk6EFv8qlrrjSn7gSq3IZu35eqheDXOMXPF9//fXv/DEnh6wZszlhTGsOsX2PvdUY9U8tZH7af2J+Arg5O7Wf+cIWY/Kqn/RrzvSBLB+M5aJzfQsX+sw4rSUx6K/3DP5zTqxpS17o5SHt6l9utOEYPfFoVx3H+ljZdy3tNG+ME5P+rFkxpT/kr9lBJvkRt/lObD7rK/Ek9pwHT9rXhj18XKsJbSTfHZuYMn5/hhmOkgd8I8f+TqzmBnl5uOQTOfYGMsSY55/x0eOj1/SVGFYxrObA3vbS35c8v8hFmACS2GuATUYmd2VjNaftLAIScqko0ekCawz4WiWh9VaYOqnaBhP6u0YMKxmLCV+rpn3XHa9s4b/jUr5zpl8xd+xgUVffxtA+Vrh7LnPIGv60y7P49Ckux65rt/E7nz32U68xpKzP+N3Fp09xq2NN6AsbfWgZh7orGe3RN1Z9M29zTq5Yu7Y31F352OmDOTlpjozf2PRhzPIi3ubGeeNAX930y/w13rQlT9ppbKwnjp3d5qTHxtocOf9SvTlIDsHEJwrwzzoNfvw5frkxP2KVw7Tlmj22U6/5VC577SJLO+p/FdvRfIGTPUFv2/nFZu8fMX8pF/oUhzE53mHb+d/Fv+NVO3KP395b6KbdxixGbe04ObJHdvFnHe384FfsOxnnm19j0H/G4FzryEPWu3Z2PTZSfsV3+xOzOUrbvQYmvjDE/s4vEKErN5lLbRmLMZordZTrPjl3TUzJIWvt91LsravtL+kffhGWtFWidsAlK3V4zpeQ5PWBpU3lSTp6aUuZ7PUpyY7R60K4pNfFjGwXr/ay6NOmz8YAlmwrfX3Ahx/aX8lrj3i7oJW38JXVhxytYkU254mhXxTau9brz9xh12c44cckkOHZFzU2j+JPWTmjTz52OUjsxijfuZZ1lPM8E4++krOUc/4f//jH0yHJeNca68q3c9dyeNRH+1Sv66rH4kC/G7LudeXEq6zzrS9f1IBthZG5zDnP+tjVT9tZ+cKndWuuWk9czYnzL9lnDOCmhn/99denHtw0cFrbO26MWQ7RUzZ5tt5Z3/Hy5PS3fzrP2pRbZdt/j5HLWNWjV1ab9IkTmZ3fVQza+1Iu2mdzkTHgq/eM+VNuhdU1+rThWB4aS+qJC/2dXMqkrs87bNgUgzY6rpzf2cn5fNY/vXmzDnIt18FkS9/O2TefztvL1W5/rOpVHTGK2dxrm75lwcoFmP3Nu5MxDVvaW/lUxjMA/sBMf6ll7pTb8ZU5adzq7uZd/5L+oRdhg87COQIW+SyOfG5bKWui8GGy1DXRl/xnEWDXDWixrWx0jGlDX61/NKFZHNqyTz9yIDfalw/HK/wZp7Z38saBjjLy272+L8Wgv12vD/zhOzdvjvFhrrClXseb+JGzRlKO57R1FL+24CH1rQ/Wu8m9P8/VHDqGS2Swm1jbXmNd+XYuc2iu2t5q3D56rI6xwTmtx+gRH303ZD3Yxdtyu3n46XjSl7WhfXxrC780ZZpr7KinTPtC3zpTP/WeHPz2T3OSay/1DDbrlWcxg00+mPPZuJUTpzErhy3ym3I86wu9HS/apDc3yNKO+m886h3JFzhbTv2MBzyrGPSt7K1ctE/tyMUTIb/9A+/WZnOm3Aqra/Tixlb7ds2YUk9/Kz3lUsa57HfYsGnNGL/nYvesI9/zjuUHGZ8Tw6UYkXMdfZuY6Lvt/CCnXvLJs7Eiw/hIHYrLOBMLGLTBs9ixjZx5zmftdK8dZFf8reLPeFi3DhKjfGiz42kcyVn7vHX8sIuwwUj8UYAmZhXsqjC0C7EQpj/H9Myx1uSra886yeBnd0i6ti5hMrHKrjDKhTFdsicWevHgI5v6YFxdkHKdZ8f6T1vg7mLdyRsHOjuZtM3zLoaW243xRZzkJL+do3/W+cjYXMs57K/wu7n1j07y8Vz81oO+HWOnm768CKvTcox3MaVsY135dg7OaPhsDtJmP7ePHiuP/eSxx+JY8YKsh+JObje/igcf7v98Fqu25GTHdce68oVN68x8tp5+mxPnX7IHq59ggkcOwExd8NUj8siYtuPGmNFXpusKPrImdrxk/ObmOf7RTzzaO5qvlZwxmVNtrmLQN7Lq3cKFuvpsLsRAD+/X9swKa9rg2dg5b498lw0dcWXuxaz9lHEu+x02bFozO5m0k/I5n887O5m3lPfZdXzYjAub3ZAzJ7lmXq/VhLlA3qZu88u6a/LFHPj8zik64gQbY9bNs/or2/qn3/GXMjyvcrHjK22ueG7b9x4/5CL8JYHsiCLwJKuJ6CS2LMldFWXa0QYXLovDdfSzwJzvYl/JGZMFph/H2uqeGPJy77r28L3iWvtuNMcrf6ti3cm3r5WuGO07D84f7dGH9//4j//47LKLPv7JFXEiZzuCfyfT+bsFPzbk3lw193Lp/BEuG5vx2jdWfSc3zuGPRn9tX2ifvn30WNmOp8cdv3rmpfnLGJA1jp5P7rWJTF6EO15tyYkYzE3aSd0dd+kPXcapp73mxPmX7I2VX0nIXoILGvnhBcqPlvkiZV755sZ8EtNOput3x0vGb26QPeofucSjvaP5WtXQLqZVDPrGzk7vCBetm3aNKTm5tmdWWNMOz/DNu89zFQy2xux88ipmsSiD79W7LNev7RHjx9+udb2s5JRpO84T56qt/DvXOjsesOta6zS/jJvHna54O8fiW/3cv/s7fcDJ6p6jffr2kWv5vLIlx9jI1jZXsaf8vZ/vfhGW+E5yAmfNF1PO87wiT5m2nWRKsMXdxKqbSddu9uiDreVW+vjozd1zFi5ycuKc4/Sfz9rKA0Jdi9Vx4pVf55RZ+dMHvW0nLwdy7Fg/6meP3cSfa0ee8cGG5XBOjOgyZj5f1MwfxQ8f8oieuc+5rqsVZr56gk+anMi1+l3vrCcv6l3iUpnEl3iaa30nb86ZQ7lKLGmzn9tHj5XHfuLsMXLo9v5pXsSbMaC7m0e/OdQPvXrGL6crHIlfvMmT3KWc9s3/So852oqT35ZetAOHlx/rGADE0L9BwpgzPmTlUV5ZT16Yh+Ockyt1VkErY/6P+m882FZ3hSHj4blrSN2Uwya4siaSC2Xp0+dRLlY+reXkDPuJoTmT1xVW1+z12fsh40puVniMj7XUW9nU7w4btlbcaVv97JuPXPO5ZYjbL4Cxtmpyk/Ejt+Kg7bc91ldx5Rwy7UsMYuQ7NnzY2i7zzK32sfFmLblv2q/26Xe5ShnlyHnm6mhtKmecbfve47tehE0Swa8+DIq+CSIwk6DcKljW2PT//d///VRI6Sf1VsmyYLPY2ocJyOQps4pvJedBILYff/zxqaDFpx3H2u/eGPxRDe11kcqb69gFg3LX/CGProfpTl4/uXHArL7+6eXFGOD1liYWsaUNc2WcrqnT/DZ+5cSNHXLV9ZH5NK72pQ36xCNG9JKn9qG9lNFm+mzM6a+5Tt/ad+5aDnf42keP9YP9tNFj5cRjrKmDjOvJwaV5+Ev+kUUX+9pwrE/3Z3JirVzi1xg6Z2lH/6v63XGi3Zfq5XiFO3kDj/VHzNnkSxvKyfEtewv7YjN32r3mv/Ek1mv5Yr1raOcXXJ1bfYtR3edyoZ52jEFOtHd0z6ywajP7S3UpJn3Tm5u0kRzDDzLgtD5SlucdthWWjh8MnS/sJUaem0dspww6yLRcYk3fKZfz2OycpA2em8fV/sB+x6WevjuGrkW5BRPxZUN3JY8M9pOb1N/lKm37rB39yFNjWdk01sShHe3fq7/rRfheoF7Tzqr4XgvPqjheC8v4vY2B3ca/zdpoDQPDwDDwOAa8xHNJmjYMfBQG5iIcmfazq/5sJURe9HEuwi9K90OczUX4IbSO0WFgGLgzA34F7tpXM+/sdswNA6/OwFyE40cy+BL8mT4Tnovwq++PLwYwF+EvpnAMDAPDwIMZ4F3D++9R33p+MPwxPwx8EQNzEf6Nvu+///7pZ5S/iM07K89F+M6EvoK5uQi/AunjchgYBp7FAD8SwTtw2jDwERmYi/BHzPrEPAwMA8PAMDAMDAPDwDDwaS7CUwTDwDAwDAwDw8AwMAwMAx+SgbkIf8i0T9DDwDAwDAwDw8AwMAwMA3MRnhoYBoaBYWAYGAaGgWFgGPiQDMxF+EOmfYIeBoaBYWAYGAaGgWFgGJiL8NTAMDAMDAPDwDAwDAwDw8CHZGAuwh8y7RP0MDAMDAPDwDAwDAwDw8CbuQj7C7/pp93OwFvj8dLfQ7+dhcdp+nuD+eX08xeaHsfzWB4GhoFhYBgYBu7BwFyE78HiG7LRF2H/rDQXNz7+9Kc/feJPbdL8k5vM/fTTT09/deil//Lea1yE5aQ/6frll18uZtpL8EtzdBHUO1nkF/5bl68Z0rUaeE1s78V3cuwZNJ9UvpfsThzDwPkYmIvw+XLyUER9Ec4LBs+8cLwMc7H76quvPtFzuXP+oQDL+Bkuwr6M//znPxe6z4evgfVzBO9zBK+vfRE6WgPvMwMvE5XnD/m2yftr51880w8Dw8D7Y2Auwu8vpxcj6otwC3PZ86WDrJdf5vMF1XqPGp/hcunL+MhFWO4excdHtDsX4Y+R9dVF+GNEPlEOA8PAazJwyouwF4/8dv2PP/749K37/nY1lxPl6HeXFW2uLiq8aNHVtt/i1u4f//jHp6+KmihttS/1VhfG1NGf9vWrfXrmXKdf2bwmo0/tcKnd8YhP5ZH7xz/+8XQJxgdxffPNN594UXXrWJor9Jmjh/vEgr9svgiVgV/st011WO987nKQsjzrg75tiBlb2rskL28pk5jbRq4Ri/748RO473XtN0505R8bNGUTS9aO63CQTYzKXsOUvrCFfPps++JUpmNc+fvrX//6xIc69sgqT3+troxZ/eTRtYyhscuN+vQrG7kuj8nxWZ87PrDDgZ8EJ0cZg3odK7py0XlGP9eRQ588qmOv/8SifzEpq51eRxf7KYevacPAMDAMyMDpLsIecPmi8cDlMPMQuyTnAWqQ9trJg1s76nggp4wHd/tmPtvKfq5rR1+s4adfFj23sntNxriu8Zj4jN04c233/MMPP3z2s5vEeM2nF97kz7nkRjzNj1jkJfHCy9dff/3ZJ0TaZg1ewGyTp/abPpVJvOpnj/2MnTVjYM1mHYibOPgRlG+//fbphZ2+1THWtCMusRun4/QvdnUc7+wfwYSusWTcYk0fR+pkx8GKV33kmWD86Xc1x3riZQxnzGEv9eVnx5v2L3GujTP2l+rTmHaxmwNrUjn1iJe1rOcewx96NLnUnnyZn5ZLP8aRueOZfKZc+9fH9MPAMPBxGTjdRXh3UDGfL72dnAeil4xM7eqg9jBH3oM4D1P0W89xy2kLbKuGfL6AkWmfOxvYVPeIzI4f5pNHce5sun601478O25OGt+KG3wyny/SxCF3aRt5Ll28/FingcGfdU59n8GaPnq8y7f69uAwR8yJD0zZtOcLWo4SQ8rz3DrMqSfXOw6Ta+00Jm3JpeNLmMCAnZUMdlZ1ZlzaF7vjna3kNWMXr3YzVvG1rnlRlxjA2pxok37HGzptH/nGkbbO8iwPHbfz1ucudnMmj6uYWxdf2m0e9Ks911vnKOcrOX2wNm0YGAaGARg43UW4Dz3TxAszX6w7uWsHXR/WjH2RebD7ctY3fer14a6c+n2Qu77C3LbwvboM5Hw+a5s+51e+lEkemRPD7gWVPlbP+MVmfsiBnCCTLbHqH8zdkvdeY5xxknti+PXXX596fWKjY2Mu8SYniQ0fl/AlJmxaS8zvYmct41KOuUstdbShv0sY0/5OLmWw3eMdruQ/ZVb68NqcG/NKXnvIGKdzyptj5zN3u1h7nhjavvbsW4f51Zzy4jM+58/Ui7E5NC73jOPen+ob464Wch5ZaqBtwYtnt/bkKvV3WJA9gueSvv6mHwaGgY/FwKkuwh5SHsCZCl+i9JfkPExXBy32XOew1Y6y6SN984y8F9TWU7YPYuft80B3rm35ougLA2P9X5PxZyuv8SiG5MS5I73YxYVOc+C4X7aM1dO/eUjfyXvO+4wdLzE8awM9PmjM+awvdVhHD37pHYuNsXFq+0lo8Q8+LtlNFWT1seMo5XkWO7qNybUVRu2v9PSRMsw5lhPlusffqs7Ekz6NN+2znuOVP2SS10vy6OtHDKu9xJxc7WJ4AvbbP80309rXTsrLn/Hl2lme4SrrXlzGal4dd5wZozI7rrWFDzhRLuflsznL/CjTWLCbeBinXse20ldm+mFgGPhYDJzqIgz1q8OL+T60d3KXDkpTqy7/OSm/Ze5BunsZ+4L10O/DVP0+yNsv+ra2hW6/9JW1PyJjjOkL/eaROTnb4dZv9ytbzYHj5pTxNT7xBybl2j9jsPMf+fCDrDFgn5csXx2GT/2v7LGWF4LEho/O0QoHc9jO3O1iV9a4Lsm1L/PatXsJo/bBt5NLGXw6lrfG4Vg8XWfq47P5Tfus53jlr3m9JJ+5O1rXuxiegP32z4q31Zw6Gb9zZ+tXeQGjcXlJdQxP2TLGnUzK97P+rYFdvjI/l/wkHnylnr4v6Ssz/TAwDHwsBk53EeZQ9IKQqWA+Lys7OQ9X+l3jwPQ/5njYI+tB3Ae+h6eyPdaPvj3Ynbc/cjB7mF/DD0eXZHb8NI9iu6XHf+dK/HLguLG2LtzkJVI8zLcP1+jNxXfffff0n83wR/OCzM8L52+8AFf7AUvWVmPTR9dF4uC5bR+tpx1HbZ8xsqvaZW3HIbjk0FisZX3IwbW8KW+/y0/6bD7RNeYj/pDpnKmP7WztC3wda8rzfERG3pDNxrixsZ7xp/yZnnf16by8GbtjY+iaWeVJ2VWvXTnVrzWhTufnKOeth732qY/ph4Fh4OMycLqLsIdhHrq89PhNAHn580DLl5AvRw/WXVrV5fLTh24f7tjAnhcJbaKXlydxr2yqc/RgXvnThv01GfFc4xF7R3nTt716cqjP5ECZaxcW5YjLhg6XvvyqvWvZ49/LIbm1Yat/g4T5FY9+M5esdb6xlbWmj+zB0TL6kyPkO3diEFPa7OdLtSv/mfOVf7BkvOodyVvjIRb00qfxsEZzLAfP9WcMyY82cw5fjDN3yoml8TNmLfGvZJTr/BpL6ovXeHf2zjDftWCcndOWM+6sGeeSi44x82Vu5Mnabv3Oz8rPivPWA4s+rAcxtM/GPeNhYBh4vwyc7iIM1R5WHLJ88PL5+eefn/o8SJHlQFMuD+VrKePw7ZeaOh6O2t3JpW8v6ch6sGvP/sjBrKwHuxjoPbyPyhzlUV+3vAzUFSe/pxg7ciCXnTfGeWEhJl9w2sJO/wiAsWevD326Jrb2jZw+Mm/KXcO24wm7q1oRnz5bxnX9i3/X7/wg3znH58rutdo9ismaJk9waYy7XLh+tE7kQLzWzA7fKncrTrSDfWNA7lLL+swaWNlfcX7J9muugdW80JubjBF85gCZ3Ded65TTLj6SP+eRzWZeWXeNvrEc4fySnrb11/YT0zwPA8PA+2bglBfhR1PugdwH+KP9jv1h4EsZOFvtri4bXxrj6L8uA14y53L4unkY78PAMPAyDHy4i7CHfH9V7mXoHi/DwO0MnLF25yJ8ez7PqmmdzUX4rBkaXMPAMHBPBj7URdhvAea3Re9J5tgaBh7FwFlrdy7Cj8r469mdi/DrcT+eh4Fh4OUZ+FAXYb6t/P333788y+NxGPhCBs5au3MR/sLEnlB9LsInTMpAGgaGgYcx8KEuwg9jcQwPA8PAMDAMDAPDwDAwDLw5BuYi/OZSNoCHgWFgGBgGhoFhYBgYBu7BwFyE78Hi2BgGhoFhYBgYBoaBYWAYeHMMzEX4zaVsAA8Dw8AwMAwMA8PAMDAM3IOBuQjfg8WxMQwMA8PAMDAMDAPDwDDw5hiYi/CbS9kAHgaGgWFgGBgGhoFhYBi4BwNzEb4Hi2NjGBgGhoFhYBgYBoaBYeDNMfDuLsK3/F5T/948f9/+TH9x7qy43lyV3xHwLfV1R/enMeUf+GDPzF8gO01aXgWI5xQ1Me1tMGDOXvKd9xHPTn7/O3cKePbjL3/5y9sokg+E8sNfhD0QHlGc/mL6Wy7Xj8T1qPr+5ZdfPjMNp2z+13xBmgMPIfpb8mFgL3GYi/lLcIp313+JDy/Br5nXXVy7+TPW5g7rc+apx3vWNraw+ZzmWfWW6uE58d1btmvx3vav2TNfj3jn6ZvzhUtgtpc4O9PfSz6vzlMvwbmfmEN22rkY+PAXYQ6DR/3J5dXmOJr+R+I6iuGonHHmhkf3tS/CXtgaF2Ne+Le8CNB99FdA5fOsF2E4eCS2o3V3RM6XUef6tWvzCPZrMtR31uKX1I083ZJbL1ZzEb6cMTnuWrysdf9V/D/qnQda6mBl/yXOzvuzdcziau/teDhmcaRekoG5CP/lL6d8qXNYvZXLhocAB91Zmi+dHSbmV4f1Nfzv+TC/Frvrb4kD6+C1Lx9y9+j+1kspL23OG1/e9EfbrT6P2n8vcmepxUe/W6wh6iLbWzo3Evetz4/m+VZco/evDJzuIuxhkd/uYwNla5m80PRm85BOGWx5eUs/KaOe67mGvpv9p59+evqqTK+Lt/G4OdTXvjFew4WeOvR9WdZu49r5RZ7Gunbzq0y9hkzG2jwlJrGsDkR92TrBsgAAIABJREFU0Rs7voyfucSEnFifAF/5B93E2eLWkL53/LiuPmP5EV/jkpPW1YYxygE5/OGHHz7Dq59//OMfT/46z9jCLzbAYUNPu5fiR14f4BETc8alHeOTM+fpE5d4XM818YLppWqz8YDL3LHW/MiB+OmTW9cvcWQeXqu39hL3ESzWAjmGI8bdui6U0ad1gh5r8KeMtsxJ47O2zE/aMB8rW51D9ay9zJm+2w461oO1qc+2L07XO8adP32nHrG6v8HU/KLTre0kjx1DYxdbYkgZ8+h6rq046nVkiEN9ezGyRsy//vrr07nh+nPjbE5WfvVJTy38/PPPn/m0PtJW87OSWeVfX8ZnTo2v+yO85T5IjPP8GAZOdxFmM3IY2dycFpvFmoWSP3NlMSJn0aasdu3dKMjaPGz0ybwb3E0Lrq+++urTt99++7TxV8WtXvrXdsp3jOitcDHHphKDXLStFS795ubGHrrEYKxiIV4blzR82VhLO+JIHWTxmdiUS139JUdynXNiRf5a00/qr3QyDvlJvGKTG2ygo92dn0tYVzW58p1+xIFctpRZYbmEo2NxTH0ZH3MrG+lXPMidsTblG3zZujaVy9jNC/HaeD7CkfIv3e9q5RIOY5cj+tyj6MqFNUi9oUdrn10L7RsOL9m3llNGH52f3K/6afuM0cMeuWPcTfusywMyyKYP5C69n9RZ+WuexYCPIzUFrsbCWLxgW539+rFHPrll3vxqizlxmfOj9pFPnPrFHvi++eab32unY0K258xNYtPmSh6eqSGaccGvcazqy9yA0cZz8iSOlFGWnvmsT/CmPjId2wpL2pznl2HgdBfhVdhZYBbsblMoi5yHEc+71sWq/S52C9ZCd1OsNnz6Ek9vTDelssjlpmlc+uu4G69yjcsDIf2qa0w7LM7b60NbctOcsZ44wJ5j7TW25gI5sbYPbWR/VDb9NAbtpQxzjJOvjmnHhfY6r85jN7lJPyubxmg9NA7srvT0R58+HGcNMqcfZG2tZz2IRbnWVS7jRHbFvbrJNbL4boz6o9cHNmnaaWysJ46d3eZ1JacP1l67gfcSPyt8zUVziM4luylvLpvv9KsMvQ3uzHVzrkzrMc4cKtc5Yry7AKtjDJ1Dcys25bNP7Mzv/GmruUG+c6aseMTXuozVVWbFSeJNHebbl7KeH8Z+1P7RvKx86+NSnOKzb/6dp7dm2p5+5PdSDtBtLtKHz42jeUaOucxPj7U1/csycMqLsEXH4eWHmz3XKPJuFuN33333+wHRMjnuYnWDrGxn0SrH3KUmHnDTdodE4+jxTg+buYl3uFb6col+tvYtbnNhb+w7O+2zudBnH8QruZ0PbWTf9nItn5O3xqpcc9HYmm/H2Ot2KQb85AHZfhpH4215fe/mWe+1HiOzwtxyjUXf+nDvyo11o9xKf+UX+eaBOfStSXt9WAuOVz53vpBtzB07Mpf09fcSfWM96rNjWsUjx16K0rZ++c4RuW6uU5Znc4LfHKvXeNRvvVXdIIu+Nbcaay97Y8Bmt7YnP9Ya/RF/4jdO/azi1QdrtF2sOW8MbV8/9qwnXvVWsSPruaTcNfuJSZ/094ozbfIMHnIgV7m+wyK/1LM/ytD6yjBv7CuO9NfxNc9ilc+0r43pX4eB012EKbQuagosN64F5EGUGxNZ5+kvFa6Fmbb1v9LDj0V8ZGNgvzcHdrWRKe9Nsxqv9PRhDDtcK7/yCMZsGacy6VsfyNGUaTvpU5nVi9QXhPrN2SUfidvnS76UocePvCXWlOk8rLDlXMunrY4z15JzsSVXcg5OGvKuG2/WfT4rl/5WPjIOZbXNmq3lGrty9MjKcceg3Ir7lV/k05cyl2pTztHLlj6VyRiVFbP6HTty4ljpa+fR/aUYLvlWL+vFZ/OmPpyt1uTItV29aYcePrWfuZDLlQ2xynPqpW3Wtc38Kmcpz7MxYLNbYyVOMSB71J/4rSX9rPDJg37Qkd/urf9LMeiLPuNhbF53sT/X/qW8dF5viTNj8Tn5SR87LOjJ+9///venemleHSN3iSMxaI+YaM2zc/JpPZhj7Uz/8gyc6iLspshChhIKJQ+2pIk1Cytl+YF87Oz0tNHFeukwQVZfl+S0LZ6MZ7cxG0ePd3r6MM4drpW+fPdGzDhXB4A+kKPt7LRP/CQXT8qLrxCt5HY+tNF910Wv9yHUWJXvPKywqet/tJEXbdi3T+fpk3PGKz/M8SEX+KU5Zu05rX30eGe75YyfuuiG7GvWppx3ThLzJf661jv2HUfNwyPHl/Bf85s8pKxxW2OrNbigKQvHyHOBaL5TP3WQx462WFtxzLy5VHaHnXVr7pI91mzGsIpXe1yYOL/6DHMdfDTGLcO8+JublXznFJ2MSdzZX4oh5drWJT1kn/vOu5SX5uWWODOWfsZ31t8Oi37B40W485K2L3GkXOexeUYu+RQDetNel4FTXoS7MBjvDoEu0CxGD57efEl5F6s6jcGi1Vb7TZv5nHiY323MxtFj/TGfrfEqh59sK7/G1LHiw8NvpacPsezstG7abWwcXmJuzpDd+Ug7+SzGjk0Z5o2RucaqHJiz9i5h4z8d8p9B8L1r6Kc95RrPyg8Y0aXP/3CCjcap3Ut9++gxuiveW06urQd9nqE2xdDYOt/EtMoLelknHfuOIzl4dL/Kz3N8ruI5ElPqmX84pcFZ7ucdHm1Y08o1585jP+32GDn5yFzqh7VdMwZks1k/zGu7ZRgf8aetrkX0fa/ou32JT46Vy/6IDPL4T7zi6rjEILaj9sGYe0aM94pTe6tezMZijTTnxuL8Clva33GUMm2jeUaWueQGncxF2pvnl2PgVBdhwu7CoHA4/CwWCpJfhWJbFZYbF5ndRkh9bTu30gFXFrAbCdlLrTcH8mlH3d40PUZOLvTppk/8O1wrv+qDMVtyqj3maB4I5MQ55jtvzLVP/a3wJobmDFvqKieuzDVy2fAPTnVcY5wvVOYbq7LEmHhX2JBFDpuX8CC3wq1u1sXKD9xzAebC3TGZl2v+jYu+ffQYmeZ9pcecMcBj6iV3xq7Mk+CG+5Vf/ciT9vBNk4OsTe00L51vdVMOmbSFj6McPQF68D+72NKteZGjXDPm1RpyzMs13+3AH009a9A8mFdxZe7Tr8/y23IrfX3oM3Fkzow3ba5yJgZ77fe5gK4cIMs4bT/Hn3ElXm32nLIZb2MRu70xmAfnuwdzxsC6uWDN1v6O2lcubWETe/eIU3z2GW/7Nq7ModwmB+ol39q319ZOpuNb8cxcYnEvJRb9Tf9yDJzuImyRciDxwcb58ccff9+4FqPrq4OrNxsFityqgFfFCv1uDP10obqem3CVtt4cyOdGUKdx9Fi5jr9j3eFa+ZXr5qU3a/skH/hFzuaGhi8xrXwibz7kNu24rg3tN1bjbDnl7ROX/lY6O6ydh86nfsSDnWtNWfHg46gfudv5cV3b9Jdkk4tVbM07sa3kmMdP+k3brBt342Hce2LlFxvwlLLtc1Wb+gUb2MWadpjTZ8bQWFexq6ftJwcv8A/+Ems+yz18MU/frbnsdXn793//96c9vbKPjnLJlXPNcfpwb66wIdfxreT0IzZ0kMvzmjn5SP/5rB1iSL9pB3lzrT/s5vtJ3Dt/+kEfPzt5/SjzJLjYY2lH25kH9bJvflxT39g6dtev2ccePrSj/CoPt8QpXnprSF/JB+v4pgb9sTXlVvkRizL0Xb9ykDLWZce34pm5trnyu8KXcc/zfRk43UX4vuGNtWHgZRjoQ/C5XleH5nNtjPww8JYYOFPNe8Hx0vaWeBysewa8CJPfacPAjoG5CO+Ymflh4CADvND5CsGtL1G/ItBf/TnofsSGgTfHAHuFPcPeOUObi/AZsnB/DHMRvj+n79HiXITfY1YnphdhIL8td/SFzqU3/zIVQLkA97fLXiSAcTIMvDADftLHJfhMn/jNRfiFC+GF3M1F+IWIfuNu5iL8xhM48F+Xge+///7p59SOovCFmz9j1j+Ld9TWyA0Db5EB/vDG2b5V7b689bs6bzEPHwHzXIQ/Qpa/PMa5CH85h2NhGBgGhoFhYBgYBoaBYeANMjAX4TeYtIE8DAwDw8AwMAwMA8PAMPDlDMxF+Ms5HAvDwDAwDAwDw8AwMAwMA2+QgbkIv8GkDeRhYBgYBoaBYWAYGAaGgS9nYC7CX87hWBgGhoFhYBgYBoaBYWAYeIMMzEX4DSZtIA8Dw8AwMAwMA8PAMDAMfDkDcxH+cg7HwjAwDAwDw8AwMAwMA8PAG2TgzVyE5/c8vsHqegBkfyH/c/8WO3/w4qP80Qr+UEH+nuLncvWAtI3Jd8gAv6PVOpsauy3B83tub+PtVi1rln7aMCADp70I//LLL2J86u99EW77nzn79OnpT39yyM+GaWZed3zLRZja+eqrr37/Jf4ehr7Esz9zvvlLdsR/qXEJzj/QgTx6H7Fd2+MfkZOM2b2U9ZLrl57dQ2feL40/6+FLYm+7zxknBvTg756foLf952D7CLJvsW4/Ql5eO8bTXYQ9oPrPb97rIryz34ngK4hzEW5WXn9s/p7zFShymfW0Owydv+Vi8GhmiOEaLv/kM7IfuVkjmfOPzMcudnm6Vlcr/f6EayVzlrnVvviS2G+Ja4UBO/e6CBvP1Pzl7HjG008bBmRgLsIyMf2bYMAD/+hF2BdQHnyXDkPlj9p/KdKOXITv9cniS8X0KD/WyFwKHsXwp6dPLM+2R3bRuqdf8xPEHQbOont8RXhqfpf9z+cvnf2fS87oIzFwqouwL/L8VrVfrXCNQuZAU6YPY+Vcp/cAXK1pv5O+OqB4sa7sti7j9tWHnfbpwaDdjkfbHnQrvPKBLZqy2kwOtEcs7cvD2guEGH/66acn2Y5BW/TqrnyKz7W2c8kPa+rR//jjj09YGntiyWfykD8WwZo26VdttX4tn22HmMkVtojXGOQ25S/ZXuUSW429OdafPevZspbB98MPPzzh1K64wZYNPWtQbMwhj6+Mz7kdhrTLs/aUp0/crqcP9OQPWZ/Thnjb34w/v9Amv11P1sVqnye/nfNcg2/sMvfzzz8/9a47j37uF/0mnt771MMu340HOfXR89lakIO0h2+b8TOXfvtMU57+EgbjpW7THs/ZMn6wpb8jNW9c8r2yLddtL32hp63GqF7y1X7wb8xy3HbQ0dYlmea1/YpTG+Sa9wdjY0188/xxGTjVRZg0WLy9OdwYX3/99e8vRw+llOXShqzNzWLh7+wrb498HgBsshzjG1urps/cmGDMDWg8ObeKJ+2rk3aNxwNdG47RF0/yxHPKIKeucvjjEvntt98+Yc/4V7jUyzWeuWQlV8jlgbzzI+6MF104a+zt0zE20hfz2qVfteZZ+RWOnQ11krO2m1iu2Wa942js2k9MzmnfeklbymQtYiOx66tzx5hcYA99xjT8pb4+xKE9e2sv8yqH2hS7Y3Xb9k5O+en/jwHz5/5k3Purc4l26zGHXNaQecg6IKfUCnlG1jo01461hy7nj3Vjrq0BfHC+2PSZdWRtaUPZjkG51BVX+hO7c9jjObHrw17bjQH7xMg5yzPNGFP22hlq3IlJ3/Yru+oZs/Gmb2yu8tq+Vvb1Ta/trIeVjnLyIXfpD3yX7BhX5kRfGUvim+ePy8CbuwjnBiVtvSE6lW4IN1GPW94xmzA3GvoeFsqs+tWmRU6/2nBTPieetoFd7XhogDM3vxibp1U8jV3byYP27FeYXNv12hWz4/TTWLTlvDw6v+uJu2Xxe+kw1Acc5XP6uBb3zkfm5zm2iWOV18Qkj/LKmnPWGWvJs/qsJyc7ucSPLmP06G3t0/lLMbTd1BGvnKcv5NrfTk6b0/8fA3CZ+2OVh1Wdtl7nQA+t677oWnae3qZu4mNthVEd+q5d7bgHlO0YdnbR6xpsTLv49bXDsIobnR0W7elPvo7UvDKJPe2IEd/ZWs9xy2mredbWkVh3GDKnOz95vmTO9E/PfJ5zuTbPH5eBN3cRduObstwgzrmZKHg/3Py7Tayufdt1A/XmV97eTdo4Wc/NuZNrv9q1Txva9KVyKTb9oU8jDjnRtrwZY+sol70yq3hTjnVzYS8WbThGz7m2a4yNPX3lMzZbVixtW73kYYcDWWz7glTXHturNXTM13Nsp54+ul/Zcw592irvzDcnO/zoi197OdbWKvadTXNq3WHDlvh3cimD3k5Om9P/HwNdDz3e8dlyu9yij6w10nUmkpX+Lo+rvcCc54o9NmnuZ/eAPjOGnS9ks752cjsf+tqtr+JGZxWj3BkfvTHtcOnfHvncm+nHOOVNHfGot/OlvphSn+cjsWqjMeT8zk7OZ24TBzLw1vZTZp4/HgPv7iLMJlwdEF6Gdpu4U5+byjVtY197rtlf2mjoe5jkxlaXfuU31/NA7Vhc4xDopj8PqdVB0frqXDo0LsULBjEaN3PaFYvj9LOzq70d/x03Plp2Z1td8aB7SZb1jEt9evRWa+hcuxSg37ZTL/3ks7jxbXMO/UvcdZw7/NSN+PGxqiN8sUdWHytOuu7ETr/C3/WdMugYZ8ul3Xn+JwOdvx7v+Gy5rtfkF1lrZldXq/ldHtOXtaN9/HYtK4NetoxBGea6ZX3tMKnfPrS1W1/FjQ52jEmfuXcSE/LKrPCLgT5xtE7zlnrJeesp15ictz8SqxhWZwdzrINltw5Hf/3rX5/O/D73waF9+mnDgAy8q4uwmzwPAzetm8JxykhG9myUPHh6jY24OvQ8DFYbLQ+Tndwlv2IAO/Hw89D5H8EuxaY/MWsDHVvzp84qFnWuyaDrAdY6YlnZWM2hb4zmU5u7Hv++UJRZYXKN/kieWi71ecbHqn6wLZ5djCvbqde+HK/sOYf+Je6akx1+6kb8+F3V0RGsYqYXF7a6rfC3XMpcs9f2P/q489fjHZ8tt6sX9JG1ZnZyq/ldXVBf7q18NpfYyjPHcw3ZbBnDzhfyWV87uZ0P/e3WV3Gjk3uo42lMjHe49J+9cff7wzjx1y153vlSv3nW1tFYza163Sc3vebYGMGabcVlrs/zx2TgXV6EcyO6ab04OWajXGq7TYvOJRseeG1fHXF4aPShc8mveNH1P7FpzzX8+tJxjj4PMsYrOTGJ3XFjTLu7eJVZxaNd8+Q4/ezsOt9x6697bOcnC6zjJ1+UqSMWOdCfY2U7n87br+JmLQ/x59hOPX10L/bk0Tm5pl+9aJhPTlYcGXPWF7x0LvSZOBprj7GTdl1PvPpvf2I1RuU6Z9qc/v8Y6Pz1GMkVny1nzs2BHrrGydWq/lbzK7/YzZrguevGeqCniaGxdQyM21b722Ha+XgCcAHDKm59imUl03zvcOk/e3RX7w9jgIds2nbf9VhZeW+ec32V+8yhGHY2sGXs5lf72aO/85XnXOrM88dl4HQXYVKxOpB2xZ+HxGqDYovCdxPv7HcJpF3WctOJZbdZkcVnroMjN6Y20q5+Uq5xMTbO9sGaB0nGu8LTc2nTg3CHsTFpS71c14ZciC+xK9NcoINczuOD3xxifOo6Tt/JR9oQb84hq7+OQ3ljQBaZS3lCZ7WODV9w2DlqWzn6XZOLlHFO7PK/wpBcK5e8yk/qwkPKiO0aP8rZr/wZs9iRFYMxqpf1hBz+E6d+pv+cgc5fj5H2bGDNtpLr3KiXeSBvq32xmlc//eIfP9qwRqwH6z1rWTtdpx2DtZRy2rcGtdWY1FVOnuzVS9usreI2RnkzJm3r69aaF0vri6fniVW+jQcsyfEOk/LabjvMY8tYHafttOHzCpNr9OJJvuGRdwcYrBfsXPOVduf5fTJwyouwRUyBWsgeBhaw6eiDJHXRp9DZaNpBL2VyXpv0aTflsandlO9n8SqfGx1Z16/F03Yd9+HhPH0edPpvP8h5mCnj7+iFM9oO49Ni/aOstuixT8N3zuvHdXVXGFsXHT7Mm7qOC9bTEHljWuER2yUb+lG289l+wX3k0EfvqG0P7ZXdtJM8aluuket6xu4Kr7rGjBx2Mnbmdrx17rCD/K4drVtsiMmXGph2Me7w7XB8pPnOX4/hwrxk7lZyyHbOm/tVnanXdb3yiyx5TlnGq3rAly1r2ThWMehTe/Rpx3VtaN89lTXomv0Kw44P7OQ+Qy4x9RmKDzEg17yLwb7tO0+fOLGVOFIODsS024cpfzTWFYZVTM0JMpkXcyVG4vD3V6NLMwbHiXeePw4Dp7wIfxz6b4vUA+/SoXub5fepxcHePx7xPiO9PardS+p2i6M5DAwDZ2Rg3h9nzMpgek0G5iL8muzf4NvPcnefpd9g8kOo8ElDfhXpQwT9jCD5ysi1ryI9w9yIDgPDwAkZmPfHCZMykF6dgbkIv3oKjgPwW0FzoTvO2Uj+KwP9bUA+SeDbhz3/r5ozMwwMA2+VgXl/vNXMDe5HMzAX4UczfEf7fEvr+++/v6PFMfXRGPDbov7cHP18YvXRqmDi/YgMzPvjI2Z9Yj7CwFyEj7A0MsPAMDAMDAPDwDAwDAwD746BuQi/u5ROQMPAMDAMDAPDwDAwDAwDRxiYi/ARlkZmGBgGhoFhYBgYBoaBYeDdMTAX4XeX0gloGBgGhoFhYBgYBoaBYeAIA3MRPsLSyAwDw8AwMAwMA8PAMDAMvDsG5iL87lI6AQ0Dw8AwMAwMA8PAMDAMHGFgLsJHWBqZYWAYGAaGgWFgGBgGhoF3x8BchCul/uWd/JvlJfJqw/wb8POX5V4tDXd1bL3NX3W7K61j7GQMWOdnPFdPRtXA2TDg+2/+8M+GoJm+mYEPfxHmgOYXjduOHtj+lR7+KtdLNA+Bl/L3EjGdxQf5J+8v1fyjFl5+rbk54F8qA+/Dj3WTfxzFmjoaIRfT1Pf53p9oi/U5F+F7/sVD/Oc5f5Sfkfs/Bl76nPw/z/988h0452Qzc+6xe//eZ8o9o/7QF2E2VP9VLZN27cB+6YswL4XGes9C+Ki24PWlN6gX4awxcDz3EvNRczZx/5MBzqCsIevqOXWE/kvU/9FzNXN7r4vw6pxPP/N8nYHXOCcb1VyEm5G3MXbvv8Q5cysjcxH+4x8/scFsJi1fMK69Zn+Gg+g143+U79fgdVVjXGK++eabz2rxUTGP3ffLAPX8nE+Yz3wRvleW5iL85Uy+xjnZqOci3IzM+F4MnO4i7Fc1/BYdfV5K8xLB5kw5DjwaPfOsZ9M2XzH593//9890lU/7bjzW+uXiWvpEhjGf+Yhr9dUZfSiD/A8//PAvPsDeso3FWNMWcdpYB9dPP/309BXHjkP7q8/W5NcYjVlfO1uZL3CoZz6uYcq4sdUxtn1x7nCt/P31r3994kMde2SVp78ll/IvtxkDzzlvnpyTI+enHwaewwD1s9rLOxvU407efdtnmPuN3jOVZ+fdS4xt1nfuXZ6VpW8c7kNw0Bwf2Zf6bR/4SVzYuoRBO+JvjKwbN7Zoyqbd9Ol6coGefCtrvLuzO31hq2Np++IUV5/fK38vcU4SB9jg9ueff37qVzzLDzgzlq5P7NE698kHz+1D+/L/m5knOy0r1y3rfkhMysp729Ivctmw3TnK9Y6v7aLP3IrTxtRxpJ+j+IzdOBM7WJMTsYEDOXUyR2LQf8q0PWVv7U93ESZoNr5NEjJRFkAT28R3YZh8C84k4MPmIfXVV199+vbbb3//2VF8pj1xacsxyXLOwsjkOpfYkUcv8YvH3sJB38Zc+hN72gGXsex8iD051pY4xZgy5sF41cl4wdr2j2BCT/sr3tMHn0Tg28Za6+w4WPEq3uTWvKXf1Vz7ZgyH4MEe4x1PrPExbRi4hYHVHr1mh3rLvdLy7gX3fY+tZWrbswIbjUU565sx+9bmetvos4zxtX2pTXuwpB3niSltiWEli07Hzpw64vZMcIyMXGTsrDsWT9tnvDu31KHHDnFkHrWVPs58TsIR+OGlYzFWY/r6669//2RGvjNOc7Liw7xoC7826gHbaUv71r+y9MilD+bMtXaP1NgKC7bQ3dUiMR7ZPytO267+VzGCw3VjYo6WduRcfln/5Zdf/in4G1e5Jk8Zn34Sh3I5B+/USNr73dGND6e7CK/iIPAMelWAFixrNAnM5LUd1jIR6K0SynwnybH2HWfC0Mticdybh3mwNRbmbdhJvZ2/5kG5S7ZXMatHfG1TTK3n2Bwopy25cXwJE7o7TrCTLzD92Gu/c7Py17xiQ33xapdx2gBf5gQ5uVIXGbAmJzue0Ek5/U4/DOwYsN6osazNnXzPW5/o50fWYdY983kWW8u9D/CDrJiUS7uNpc/jHh/dl9fssr6zJZ8rnMaQ8WvHswa9FRfJoXbah7Y8OxzLYcflGDsrGeyQU7Epb6991x3vbHVcyotXuxkrcytO5FldMIC1fWiT/qi/9q8NfdC3f3FyuSS/rOuTT0bw3S3tuUas1scOr77Nv3LYy7aLI2XyGf3MnfiSU33Ju/qMU855enUu4TOmtqud5IU5sbXNrJXdPtGXPOvjS/pTXoQlIA/mTFKTCgHqWFyS1eNMFEnIwlnZkVztqd/F0WP10kdjVIYeu42l15ODtJtyPGcxiUvcLeu4/TPWnza6aNFNvV186ouhx2LofpVnZFb6YMt64fmIv4xT/9rveJPzXaw9n7nQvjLic57xPTe3dqf/GAxYt8+poVV9NlvWK3uqzyjXsNPNPUm/k6Pme9+673K/Ydv4XNdfyzlvv1pfzSl/iRPwJgeMPSd3MWJX7Mjv5FKmdcS26sG7ynnbQ5e4m28w0Vby+ss4nVMem9mS212sPS+utpV2j/hDfseH73BrNeVYg8Nff/31qRcHca+4xU/bcyyfyUPGIUbrZhcXdrLW2gZjZDqfYqdnzTHyO0y7eXSO4DOf7U/MyfUlHMRzjRd97fKiz+f0p7sImzyLlWB4lhzHTYLkpF6Sukr0am5lB59d5F0cPTYJ6UMbiVG5a0WfsaBzST752uEHmLZOAAAgAElEQVTSr73YsNscmBP6bomj9ZQVA7I0xyt76tATR+eZ+RXWPDC0f8QfMllbl/CtctmHkGNzvIuBefEZM2P1nJt+GHgOA5f26soO9db1v5LTbtfnbs9jw32Ibsu5h9O3Puhp9Kt97bo4W855+9U6ey1tK0t/iRNxo7+LqTnCplys9PSdMqnT8Spvj7+3fk6ucmR89vLTfKSuObnEh/lBz/rj2XlyxAeNOZ/FkT1raSNrirUcpx521dvFdUnfOtQGtokhL6LJi76x6Tuq+x3Wo/jkXrv4shFv5mSFDVl0jKnj0ZZ+0p5rt/anugjvAsyiIdAmlTl1WbNlApnPNWRWyVjZQdbCM7lpm/UeiyF9aKNxIIvdXSG6boEwTrv6sse+sjtcymaPHsXFz2jnt4Mu2UjcO+7U33GXGPJZPNjNlvZWmyXX0XOMbDcwyZVrO/nk3Fwak7rd72JgvnWZ42PaMHArA0frUvvUW9e/a/ba5Ocn80XL+m7Ps5Z7s+Wo/T7vUl79lDmyL8Wcfe5b51dzrl3jhPXVOdkxao9e7MS9k0uZ1AHrpSYe7GZLe80tcrme45U/cHedqN/yjM2btdNnXeLkOXV6zfERf8ju+BAL6zTG/qYe8IkRLOSXrw4Tc8cnHvrEhF1ts3YpJuTkM22kbfDIY87zvFrDX+7PlX/09Ns2d+Nb8BFfYmecF9cVNuMSX8cjPvdP2nPt1v6UF+EsJgLLonHcJEjOShfZVUGvkrGz4yZys3Rx9NiEtI+ORTnms3Cct+8C1p94lBOnPCgHjmsNWf9zRvLbNrUjV8r2WDkLWqxHMe04wY5cNb/41P4Rf8i48cSrfnPWvsBn7Op2f0QGHbkTc9uZ8TBwhIFd7e50qc+u/5ZVxm8bp7x1m3Pqq8f5oRxztNW+85xw3/V+28XWcvq3X61rq/fb7qzTFj26q3OStYw5dfDjmSUXfXaAk4uMmMTI/KWGT22nXPo8wsElf9jqHO/k2xf4OtbEyXPr9Drjo/4y7rSDj7womofvvvvu6T/GY59GDXBB5ueF6RlfasYHP/iwidd8Ot81tpPb5RU7q3x0fCtO9ZU4xbXr1ek4LuFTRz9yBOe0FTbmM67mSXzOX6sp5Y/0p7oIAxjCcsNBDMWbc00qehY1a9kgvPVdN1mZ4J0dyVdWXRPdY310wpXLJBrj6jDTDjLJAfPqiUHsKac/ZbS36tXPw1g59HserhtzY5K31D2KCfvoJVfqmmfH+KU9159xJT/azDlsM854lROLXGXPWuJPjDmPrfwqfNqY52FgxQDfuaFubNZ+1pX70f2hrD31meeF8/a9P7rm88zIfaCefpVTxnV6mnbZ787Rr/ab64kx5Zy317ZYnJcb7YnxEh/oKpdnmjZXOcB+y7Zv9VJO3OLTR/dwil7mXV35diwHz/VnDIlFmzkHNsaZD+XE0vhXOisZ7VzzZ34yj+o2Bvjwkxr0bMj1b5BwrXvwwH/6U6bzvMK2mtNm8qhNetflwvjA4Rz9Sp/YVvNpP5+P4KOe+DVtNuJOH/jM+txhQy95lD96mli63vV7a3+6i3AGarA//vjjZ+Q0qUkQa9nc8BKZazxLtAWk/2t2LDyLrsf6WSVcWXzyAQY+sgDUt9+tY1879Fls6OpLnNrb9Ts/aUt/O7xwpwybAd/IYjvtXMNknnnhY0eb2jGG5oB6gQflrnEgXjfuTh4/yujbehEbfcoYA3I27Sd/YO3cKT/9MNAMrOqO2qPeslFXzLsXco1naz/r1xr+z//8zyfdnU3mxcFz78Pc3yknBrHpD3n2hHr0uZfcN65rp+Wczz59pT7PGfvRPYi93L/py1jTbvpUNrknTmQ+6jlJ7JlrOcr+uflPfsnFag9os9esi1XeEhPP1+4Y2rIeVjWmjZThPXaJk6zprB8x0+/0GxN+4WvXruFb2RMHNrGdce+wrfZVx8l9AFuX8O7i2M2f7iK8A3rr/IrYW209Uu8MOC12sJyh9eY5A6ZHYPDFmQfHI/yMzWHg3gxYu/d8Kd0b473tzTl5b0bftr0zvLvfNoPPQ/+IM+ddX4T9LOUsF7tduh+R2J2v3bwYdl/l2Ok9cv4jXITlPT9bfiSnY3sYuCcD1u9HuQgb75yT96yit2vrrdwx3i7D/4rcr+Lf8wtH7/Ii7GF17cv9/0rx42fAxpf2s/ES2X0LI+Ue9exmfk0Mq9g+wkV4FffMDQNvhQHP2o9wEZ5z8q1U5eNxWvdnvGM8PvqX88B/0OXD5ndj7v2Fo3d5EYY0/scnnzmcrfnZjD8LRP/aX12guL7//vuzUfUvP1d0OoADaBj44Ax4IfgIF+E5Jz94sVf4Z71jFMw3PeS7+XlXetQnHu/2Ivymsz/gh4FhYBgYBoaBYWAYGAYezsBchB9O8TgYBoaBYWAYGAaGgWFgGDgjA3MRPmNWBtMwMAwMA8PAMDAMDAPDwMMZmIvwwykeB8PAMDAMDAPDwDAwDAwDZ2RgLsJnzMpgGgaGgWFgGBgGhoFhYBh4OANzEX44xeNgGBgGhoFhYBgYBoaBYeCMDMxF+IxZGUzDwDAwDAwDw8AwMAwMAw9n4N1fhPP39r727+t9Tjb55e35By6M455/TeU5eEb2fAx0jZwFIb9T1t/9ePa/6ngWzs6E46y/G9gz8Ay/e/1M+XoLWF7zrHrLf5jp6F48KvcWauU1MN79Iuxf/vBF+NxfgJyHXdq45YWqrVt075kMOKFQn9P64DAWL8L08PPasT0nprcqe0v+HhHrL7/88pnZrpHPFr9g4B6+5a/38NJ5S59wsi+J1+YL5S3FIPZb+x0H9/4jGV/CreffWzrver+CnTPbM/zWfD1HrzE8R/eeso86q1YYO+a5CK9Ymrlk4O4XYTZ7HlYeYEcPVeW/xIYBYiO/qur8S/ZguOWl2geHvHiI0s9F+PGZvDV/90TmBaL3UNfIvXzeehFWr3HeC9e97az4k+tb9uy98b2EvUsc3DuPX8LtGc7yo/kwzuaPGF7qIrzDcDSGe8ut6uzePjx/4Dkbebjlk/q08VrPR/N4VO614ji737tfhFcBU4hHXyxe+LqYGR+1IYZbdNS9V38rhj445IX5aS/HwK35uyfC3SHXNXJPn7fY2r2IbrH1Ejpn4+8lYm4fKw529da6Lzk+wz48Gu8Z+DsDhuRrVWe5fo/n3fkzF+F7sPu+bbzYRfjoZ2Re+Dj4sq0u0252Psvmw4tyz7OWXxnWh3q5hk837U8//fT0mWSut219JlaeW05f2LYRk/Ppg3UxgJUmZvV7nIfAJbs73/zddDBoXznjWMVJjsCvjph2MWkLfNnUM+fGvuJfvbSFvD7p2744ldlxnf7++te/PuVeHXt8iY8eXlxb1bg4lUkeXQOvMTR2uVGfXhviQAY9ZdoGnOlLGW3IZ/bKaudIbYlf+/TqYzvx9Rrr5AhMP//881PP89///venHKCbORS7OPVp/RhL+1RvhQcb6qPXuew8dA0d4UhcZ+mbHzmQV9Yz7o7ZONLOTiZlk1vzbi2bS2zSxOI8ffroussco6/d3NvEtPOLPI11fSbeXms8yZf6YhILMrZVfNYhMq7DR2LCtli1ZX8JQ9oUH3361E72bdOYlMkawJ75cz1j53nl01jTtrJi3eFsOeTNG1h4/vXXXz87r9Hp1nZ2/tBDllq0tsSY9bmSy/XmNdfQlRNiaNnElnIZ06V4dmeWvLluXCu+0tdbfn74RZhkQeRREk12Jtlk5pxJyg3Hc24i5HNMola20EuMYPjqq68+ffvtt0/zFucRn10MKwwWrQWHDnL6EWeO5UUee6xN4rjEiXLJi7aSg4zD9eRfO8ZwhFd1Eh9+2j7jFf+JiWfztoolfXDJx7eNtdbZ+VvlT7zJ16o2VnPtmzEcgqdzJ94db3BOjYC96yJzdQSHvujbn+PG17HoJ32r23yD29rBJ/iRYQ4/yuMj/Wrvm2++eZIlFzR8IicPyJF3m3rtM/eYsuYEHRo2sZ1xiSv9iZ01G8/G4tyZevA3B3LlnpCHjkW55BSO2l7Gi42Ul9vUcX8l3zw3j8x1zrHdtowDWdf0mzbFzrmvb7FkTq+dJ/KSOnDQXLtfVnykLs9gTzmxWv/JMc87DEd9pj11EpM/h6uf5FHOEm/Hjq1cx596yNI6RtfNTWLkWZy9ji9qgDMDmZXt1dw1f66vzgbrDLvIXarBxGuu5UB+1WdMYz39Kpc5usafOmlHDskNH/KF3YzpCcQ7+uchF+EskNwgR3hLXRLkh4WhDRLTtk2ihUWfMq5nsWDPgnBjiqETf8Sn+OwbA/NdoIlBbMSb/sUkDz3uGPSvnJy0XeVYh2vtO5/Y5Ic57SJ/lFcxGqM+tCVGxxm/stljZyVzKZbGnuOdrayhlBevmBinjSP1ggy8NyfapN/xBvernLXfHmPTnHUMK3/6z/wjZ560sbLZnKBHa+yOm+sVdmX1iz19X+IRvcxPj/+J7J+fYBnrzm5z0mNtNUfOn6VfcXA0llVu1d3lgXm5hQNzSZ+t846vrI0dr50v5TLvO7/qJj5kG0vi5FkfxrDjoLne2W1eV3JiZW3VdhhWttBvn2mz48u1nV7ntWPvsRjMsT6xn42xMjnPs5y0zipmZeXvFn/qaEM82raOlPv/7Z09llxHcoW1o9kFuARwB1oBNqAFyCdtLQCOHNjjQ+bAJeXKlQudrzQfeRGMfPWquqq6fiLPaeZ7mRE3btzIzEo0mo1cg9pUX+umr+9dzviKqZ14xqxapH76GEv+2NTPlRWePo/eX+UinKK4ISxQznXPneCOWTALWDHreBadWOLAqTZsXVTaMWar2MfGna8cGIe3uWhXx+tBISe51/cVPzecuaxiWyfxkxfPqY/vbs7KJX3Tb8VRfznW98TL51Uunb/5scH92hMPG/M0tvhVK95dQ6tc6zg5VHzj2FcfxzOeY/TJeeW7Gse/ztV3Y9W1Vd+xW9VIW+Zp1qdq2vl3+q84ooX1tjfGSr+M2cUyf7CP1ds8sb3H1mmw0rLmkjplbqtxbOpcFx+7XMPd+8rPGO4p61f17/xXeVcuxMDf9WRvjBVOxlzZgF05V82w2fJfzW/51Jhg2Ky7a91x+o4b4/owT8vcc36lWbU/gDQ4jneYznUcqxbnxFMzfGsj5tYa3PJFE7WuPDMOcVl79NVuTz7VR+zO13paL22fpb/6RRihsrDHhHOBVMGz6BbFA6j2bj4wXIzETYzKIznKAXvb3pja21cOLr7K2XcvyHUxVk71XVxzN7684aGNMbSh39KG+Q7HWFu+qavx9TO+uWBL8z311zZ7cLpcOq4eLIm/Jx42uYbSv/Lj3ThysK61V4NVDpnnSreMl/bJeS+P9K/x6ru2Yqtjfddvq0bqsMql06dbHzWWXLJ2xKAO9LQ9MauPudOTt/U2vvloJw81cvxe+k6DPbloU9e1713NybnWs4uPXa7h1bvaVy2JYd27tYJ9F9ecag27OmdsY1jjFU7GdF3UWHCreFUzbFYx1KKbPyWmOPb6Wl9yMUZXa+3NL3MXM/PSHjsaWhqr9qm9WPRiWAfnMo5jcpffOfGsk5zFpgdvaw3iQ14rX3OsPDNGxq92e/KpPmLDyfiOqa16Of4s/U0uwlmwY8JpWxdzjluUalOxczEyJ8axxdfZ7Y15jMNq8VW/uhgrp/q+wk3e2nQHF/FWG1NuHij8zwH8zBIcaJWL9vTUwE1l/LqZ9Leevnd1Smz5gJtNf/C6vHIeP9+7eHUNbdnjb66pe3Krz6sc0m6lW8ZL++S8l0f613j1XduKXd+xW+WnrWthlUvn39VLjq5tNLAW8iVGrvE9MbtY4mUM45uPNuaJ7T22ToM9uaxsjuVY69nFByPXcPe+8sOWGFuXEGw6/1VOWWf8cg2B5RqxxiucjLmy6fCqZths+a/mt3xqDmB0TQz17bjh57pnnpa5i0tMP0eYd+8yX+uvz1ZvTOugbcfRPOR3Tjw1g3tt4KpRZ9eNiQEXz67KUxt64roWq92efKqP2F2t1Fa9tH2W/iYX4U7YlYAukLqYs+j4dou7YtbFsCqmC8KNKAdiZtsTM+15rhxWY9WvalY51XdzqAvVnNWT3k2WMRl3U+V4PhPTH9pXK+aNUWPLSdv6Lra1lWPNTbvaE2+Vi+NVRzDE3xMPGw804+tf10eNtWe97LFRt6pvjSe/ynlPDH3pa7z6rq11V8f6jh1z1kI/erjnelvl0nHv9Jeja61qcG5Mc6ra13i+Vzv91Sg1uIfnTve9uXQaH8up1rOLD0bFru+ugaqrelsH7YiTrYu7ypsYruHOzxhyWeFUXzjWs8Xcjcd71YyxVQxzXM3vjSlO12ceqU3aYnNsf8sRDHipHzhqCs7eZu0TB989+p0TTx/ws8nDce0yl2qjv5p4jvnerRPwHdduK6Yx7KuP41lfx1Z8nX/0/uIX4S9fvhwuRgrjIrBAjPOcm0Rbeu1zMTvm4ki7xE0cnsFwoTjnBk18MPLgMV4u3L0xjWNvvMRyUWU+2ttjv8WpclwtamOZr++pixxXNZGTMbATzzkxcrzqii3zGUc+iVlzM0btXUepo76uC9/ldWo886K3iZljzPHe1Uwu+mfPXPLPuXzGLmvGXI2nPbmmrXy3eOhLb521r+/aqmXV1vfEOsZnlUunj/mk/nJUS+ZynenTjSVfONeYYqUdNllr46vZSiN5VDvtb93LJ3Pbm4v1V/M93DttU0cx4JNrpr5jx1jWU97pZ365VvDlvcbVv9aGONqKxxhNDfL8YhyM5NHF1Df1W621tAFrxZU5W8dhb0wx6Pm1Y3zZElcemasapY6d3uChI7nxGx3wy4a/uuf46lkuVStw6pi2yfHUeOaZaxBuFUe7bg126yZzlid2ybWuE+3SpvKounU+2HS1ct2IT1/zrviP9H7Ri7BiIVB+eWgozJaILpr057ligGUh0zYXET65QY1fY1Qb5+vC3RPTGNmbb3Jj3vHkb8y6GCun+q4WYGazJqmfY8bFp8ZLjHxeaYqNnMStuoqTeaMJsbGVozhqoV/tweGA40c1wDGuONqD4xw9f1jDT7tj8eRr/Vb2nYbWJeOLAz9zwG6rZc081Lt4YHQ1OsYjY2sLN1p911ZO6ljftaNXQ3XQR5tVLp0+nf5yVBtwiWG8XGfEsqWN41sxxatr2/hqJn7VhHhZf+3es68a7M1FzrW2aKSW2thXbVd1h1NqXN/Fw9+a0Gf9senWCuNd3FXetWY1Zj1PwLfuyWkrZuaAXbaqGXMrrunXcUjfrZiJk+sDn2791jWAT7Yud+atT62bvlVr4hNr1cRLu1P0OyWesfDJ/HPdZo7Y1SaGtai+1hA9Mwb2ibdaD1v5bPnUGstD7eWSHGpuj/R+0YvwIyU+XH9UgAVdF/+PFn8e7vWQq3a3emczrg7QW3GYOKPAKQqwZv0wOcVvbEeBUeC+FPAS+yyXwftS97Zs5iJ8W73vNtqxS6V/eqx/Yn3PhI5xfk9uE3sUqArwwen/HFTn5n0UGAUeS4G5CD9WvbbYzkV4S50nnat/gvWvvuq46TPOX8Uc+46x9rfq5yJ8K6UnzigwCowCo0AqMBfhVOOxn+ci/Nj1O5m9P+vjzyTtueDi8+uvv54c69oOcxG+tsKDPwqMAqPAKNApMBfhTpXHHJuL8GPWbViPAqPAKDAKjAKjwCgwCrxRgbkIv1HAcR8FRoFRYBQYBUaBUWAUeEwF5iL8mHUb1qPAKDAKjAKjwCgwCowCb1RgLsJvFHDcR4FRYBQYBUaBUWAUGAUeU4G5CD9m3Yb1KDAKjAKjwCgwCowCo8AbFZiL8BsFHPdRYBQYBUaBUWAUGAVGgcdUYC7Cj1m3YT0KjAKjwCgwCowCo8Ao8EYFnu4i/N6/W/aW8f2dwMScdr4C/oMhq39Q5Hzkv3oS497+YZK/svzriP+y4NY/aa3NrMe/6vdsI69e61ue88+2drbyeY915e8D5nfq39O/nLql0yPMPdJn3UtfhPkX1fhg50JJz/vqUuQG7TZK+tzygJyL8GWOg6zfFuJvv/22Nb1r7pEOh0zIvcI+sPHMGrS5Ry51Ea74xjm1t77k8MzNPPfqj113nnkx6HD0+e///u/DmdnZPLPG5kbeW38o1G760xQ49wxhb3ORZQ+c0lzrj3Q21M8h9/295QCvR/mmz8tehL1EUiy+/EBwvB7wbBgOPr54zsYC1P+WB+SKa3Kb5+MKeJDQd02dL3HQEONRDge18MMp9eny0K7uHXFO6Tv8U/zTFiw+JC9Rv8S9p2fXKHnu1V9d6LOh06dPnw5f1NSW9c1n51+pv+U5/0q6nruuWLPnXITxe5TzeKWN+/jezjd4PYq2L3sRpkh5efXDw8VW/7SPPR8OjOeC017/Wx6QfvgZ+5UOzEvm6kFC3zV1zrp3dnvGiPEoh4P5wNm9kmM1j7oXtD2nf0SdzsnzUj6cAdTjw4cPuy/Cq++GgfXLL78csPIP/dpTm0vW+lIa3BLnluf8LfN671i3Xlec6fVse28NVvFvrc2Kx97xRzrD7+4i7KWDP935VS961SY/kOsB5eGdNi4oLrVfv349fIDkJafbHOAyzlfykQtFpxn/999/P2wwc3CenrGMh5849QKeiw4f8cgHLDZx8pGDdvR1Xkx16A4CY8lbHcVNPcETq8bSr+YrB8aJTxwwxa842Iu1ZaO+2tS48nQevb98+XKIa65yo694+GWNKqeqS2KJlzbJB66+kz/v8qTfwy9rKff0Ez9zkNcqBjzSHm7Ji+fKPXXJfInlWk+MrPcKf6Ulexh+4tV4ckkdwMo41cdYtQapr1oaN+f0v0VvfqxjdEgtt+LLP+2pzc8//3w4F8FKzXg2x/Q1PjqsdNzSGo3BBR9/9UxemYfrJ9ek8/gkh+TW8XM+8wQLTokjvj1xiL8659POfOirfr5rTw8XbOFg29JPm+zNy9ippfqBvwc3bcBLLGJaN2Jmw67m1/HCzlqeuq6MVzkcW1PGUR/6rHflmXPETA2JhT+9POjJXXzmaIw7dkwbMfGrfJjT3zmwsx2r2zGNEmvrucbJXNUtbXjOhr2a0OujjZp6zud8raOa6Lu3v7uLMEUlYZtFVlwTd+Nglz8zg8jOuVh9F/NYT0y+s0JPIybfDeadoiSeRdKW+PjyYUJ8GtyzeNjUgoHDIqDvmovFeXXAx4XlWGLDi9jJOfGdV1/mxNFHbmlDzOSrj1yM0eE7Ry926tP5aGf+1jbjVZ0rjhw7fTKX5MezsTL/5J7jVZeKBf/MFft8x14M9Wes5uZY8jY/8XxPjdDk48ePP6xPY2Y8xmz4JwbjNQ/GjMf6Z7/wTsO3ar61x1f4B7D4j/VFg1oDNcBcO9eOPDPfTl94J06E/mNNpC41z7S/1nPmwjolp+R0LC55pw5oZe3Aqbpqa9xjtdZOP/hUrakLNUytrVnGz1z0sabMuU/NX5vEYC73jHESp+OYsXkG59g5T+6fP3/+w7VqsYoNtnpVnz3czNucqi5iooNamVPuU+1yTM7yw484WTsTBjt95dXVQzxjHltXxrCvHIyVvOSe8XlOjubTnSm5buTJXiGG9sbIuHJBD/W2JuZNXM5E/G360dOMKYZ2xqx2mZc2GU/85KpdamScrscu/ckLnjTwmaOWcuvw2SP64FfXDT6uB3Q2nhqmHtW349yN3d1FuCNJchbQ5FeF0hY7fHIxdNjdWI1BIbzYWhR6GjzkxntXCPGYo7kAXRz6Jc7B8J//IRbFrzk7Lm5dlGJ08Zxzc2VscfGr3Fd+4shFO7Eqd+dX3FLHFQd83RSrOMR1Daz0YTwPObnZGz9zcKzmqw6ppzj0yXkVN3PXt8Zb5VvtwEouxGeML55pcs78jLuayzyqbcZjbsVVP/qOp7VNu3wWF99saiAP7cyXPCu2eYqF7daawM51ZWzjdjpqc+meWPKoOeyJVesInhrwrIZim5vvzhtLrbWjP1frTmPjqLVcGc9cunlsKm/5ujbE73g7R99xW8VMv+Qol8xBjFP0S3z9E5P5Lu45tRMr90ZiJ5fUqMsVW/nKRTvfxbNO6uK4feXAe3LULjkxBp77h3f5VP0qL9+JkZw6ntpmHGPXvSFPev3kUt+1NSY50+DT4VZN6rt4VSPHux7bWivtzsWv+fhec+p4Wr+siXy2+ru8CFtwFplfLqKcs/CZoIXhZ9z0yfm9z+DwRSOOz8ZnzOcU3fjM2bQTw2LV98TR1/h1ETBecbrYnV1i81w3Du9q5yLstE6/mqMx9D81tz0cxIYbX51GOb7SB5vu0DQHdc4cMrZ29qmLY/by4U/B8OW9to5n1VcceNSGv/WrdswxBkeeaWDwJ+4Oy7iZOz4VlzFtxT2AxzpNDG3d3/RyXuGLZ79Vg9Sg2jHXHd45ns/Gs5c7NtlW42lzyeea1znxXdvUk0ZOPoO/+gbAKpZ41nqlY453awkuYOSaqNqBkfOJWbVJX3A9K1Z2aZO+Pmcsx1aagJXrPM+ammPVootDvNX4Kp8cX/HcWzvt4ECrnNWDeeuT8Z2nl4v70XextTUmenWtcqjv+lS96/uKJ/7Yum7kKW/xV/5dvTqO5pnrxRjGrNrUmF0s+ImtfxffPK2bea16NIGrmGl3Cj62mTPPYNPMz3fGVlqsxpNX93x3F2EFSWF5zsKYrMKlQNg6Tg/eOQ1MFyCYNQbvLqyMga1+xpUvczb8zQl/N5jz2WPbzRsfXGPU2OCkXeL67DxxxJGr9cgc9Ute1U+bbhE7R7/KveqTNa3PYGBfx31Hu//6r/861KXTZytHOKY+ct/ySV20t9dPbursPD1jlWfVdysG/q4tuROXZ3DpqYt/Bc5cjScf4xIvGz51TWpbc5KDGGqQdsmZOB1+xufZtYVtbcRSg7STo/rXHh3+53/+Z7lWiGM+1df3zKvyuhk5YyIAACAASURBVNS7eWSsbuxYPH3Qi7y4+KIXLd/RWD2Z0y/j64MdeNqoS+1dc6taZw0PhMp/sq7WBB8amMRbrQ3XbmIkPDja5LjP5C1/x8xXTeSUulVeNT5xxRWv6ua7dsanF1+b2jMvrjz1ly8ctOliaKc/mJ1WzJu7vOiz1Ti+i62tMa2v4/aVQ33XDn85MVbfVzy1Nc8Vz1pP45JP1bLGggv1Mkdj6Od71SZjaqOP8enVUP+9GiVG9yxvuGfcPfjyVVfwzUcdfAfPZi51fftujtof6+/qIqwoKSYJkFQu3kyKuRRRW/4nBnBWfonRPSM+3yXj53a4MPBuo0BgM+d3TJwjfuVvXszZsriM55w29qsF5WLQl77GBqPaiZu9vuSU3x1MnmnPMzqofZcjNvq7qCvGKjfsrd3KJrHSPsfz2Rzhmg18NhB919QvczCvzgc7dal4GQu7Lm7Hs+oLzioG/mpHfN6JBWcvv+TkpYd5vlatm+/iV47ipX7a1HVKjOTc4Ytnv1WDxEs742/lCz7zlaNxMx/Hbt2bkwd/16PhnsbaIFfPOjSiqRXzfKVmzuUYPqnNyqZyWtWamLkmql/ig5G26tNpAK57Z2WXNjUu7936SD7YdBjwqXseLL70l7PvVeOOj2P4mptjtV/hZu3w6XJkXDt5rWIyb026vMGSi3vNd7Hlbkw07VrlUN/1wV9OjNX31XrQVm1XPFf+nZapifll3sY4pk2N2cWCf42xVyO1O9abjzXag68Pvc18xPE9bcxFG33P7e/yIpyLgcR4z8WbyVaRchEolgsp/Y4968uPWNTLLjEZ+/d///cDt8TK+I67oLu84EZuWWT97M2xFt1xcZl3o+pL3y22nOcZLH8gPfVSB2PoZ07a1nftjF2553zHGXtrLocVhvzB2dJxpQ/j9cNJfvRdfMeO6ZI4PMMv88U/37FhTF31V1/jWfuqSccLG/BYy2kPFmPMHdOt8ql5wLNylLuciL2ygYv1xq/DF89eDdTEceM5rp05wiNj6Zc9NrUuOQ921STn3+N5pe0xLuiCHt15hg784amukVUstcePtkfrVa33+sIdftabuPLIMcblbe1cG/I9kP7nHjy1/mIbs+NPrvWsUX/6+lnTYcix68275pO2ladz1ReMToOaQ30HzxjuM7HVpsa0Hvqt7FZ5wSG51nfjVT3r+4qnvI7xdD0RPxv56Ot46mbczO/cmGCkFl08xvZqpP+xXr7Wbg9+Z6OGauE7ttk6TXP+lOe7ughDnOTcPLwjBgeHYyyYb9++/ZFjLXoVB/HwV9Q/HHc8gMX/YU+fDQ4cWFwc9xSnLhCx5GZujnc9HHJxg8kHFBzkZ5zEcxFp02Ezpm+nlTxTw8oHDGulJm7uDlMe2GZejoOVeVRs7bLvOOW8fPJAQh9qDAd5pw/PapN+jO/VJfFqvh0n8qix5JB1rJpok7oRmxxZJ+TJsw0ujNcPX+ftsesw0QwONuMnR+bMUVvmE888csx1q48xsteG9QVHG/i5prTTRj5VY/3pzSVxcl7Mmmva3PpZzslJbbd0RI/VebZaI10s8lVb4/m+pTUxOp3ByDXR6Sl+XQPYglvPnro2zCPj6NdxkgM4NSex1F8cepprpnJVf85zfY1jfjWW811vzY1bbSpP541l7bRLbcwheeqXHOWQvo5VfPTQ15iJDz9j6Ctne3LNetV37fCvnPIdO3z3rpvKU32q9tiZo1yMQ2/eaYNPaoMfY5VvjSlW2mmTfImbmsmraoRPZ6dW+hnDGu3Brz7WOfXXBrxsjmdOOX/K891dhC0iQrgI+P2YFhUxnLNPgRAlFxNiMIbtqYJRUPwsrMLKsVscXXzta3yLXvGNU3v5ZN5gVlzeten4V1zfwVdnx+xddOKu7DI2+lAbbFc5Mt/p2HGpHOBSa92tj9THWmQe/MEKjrmOzNs+YydejoO50kWcLl856wt+zUveGRtMfc2n+mGjb51z/VVMudrrX/XJ9cicdhXPOK4B7ZJz7nHjVnzH7dWe2MQUTx07O8fo00ffmmO1SeyaBxjdWs6Y13yWT+qvhmrfxdev467Gde3ok7HArrU2XtURrdSavosN59RbrNqDXflpI3/r2+HJWRuwWI8dJ3G7mJ0m6u/aIFc4mHvipSaO22/pp032NW+w1ajjia861LVSY9d5fGs8fLr6VT34cRx4YU87ldvB6Z/nYNZr75rqOHb51HWz4qkOXX3VPzlnzdWfMb7UMP3SxvGtmGLR17rt0ch41kfu9M5ljLTbgw8Odonh70OX7yo/fK1D+uc6SL5bz3d3Ed4i+2xzq034Hnm6qF1878FhYt6vAqwLD957Ybl1QN4Lx+FxXQVmDVxX32uje5HJC9S1Yw7+fgXYX/ytIf0zt7kIv1N1/VPQPVw8PYzqn3rfSZoJe4cKuEbu6TI8l6A7XCg3pOQf3u9pTd4w/acINXv4vsvIH1Be4Q8pcxG+8Tr0QsG38u9hgXkhP+evE24s3YQbBX5QYD5Ef5DjpV74BgJn6Pzh/XHKzm9y4ss2f5BRienfW4G5CL9DBfjHFO7lrxo4jH799dd3UGFCjgJvU2Auwm/T75G9qX3+88WPnMurcPcPL/nznPfwzaBX0X/yXCswF+G1NjMzCowCo8AoMAqMAqPAKPDECsxF+ImLO6mNAqPAKDAKjAKjwCgwCqwVmIvwWpuZGQVGgVFgFBgFRoFRYBR4YgXmIvzExZ3URoFRYBQYBUaBUWAUGAXWCsxFeK3NzIwCo8AoMAqMAqPAKDAKPLECcxF+4uJOaqPAKDAKjAKjwCgwCowCawXmIrzWZmZGgVFgFBgFRoFRYBQYBZ5YgYe+COc/TsHvJuQfh7hU83eUzi9t/1FRNZ9/zelHXeZtFHgWBdzjj/o7Xvkc2PMPBO21e4a6+o9XvEdNX0nnZ1grt86B3y+9Z79ek9fDXoQ9rFcXMufP+ZeHvATfwz9/vLf4v/322w+m/vLyS/7hwABqm9hq5i9LrwsbW/+wwmF8Tl2MP/0oMApcTgH2Mxclm/v7PS5NcnhLv/fitdfuLVzuxfcaF+HVZ0z9LHolnS9V76rhpXDvEWcuwm+oihev1WXVw/ycC9c9FGavNOZZP7RWh9Re3GN24OcfQuqHKXzyMsw7Xx7IHI7TRoFR4H0V6C4pqzPlfZnuj97l1Hnvtet8H23Mc7d+Trwlj/oZYwzGs72Szpn3Oc8rDc/BehQf1kveFd6D98N+R9iLMJvs0o3CnHOBvjSPPXjv9aHFhv3555+X/1Q0dfE7wHJkjLrhh/+0UWAUeF8FukuK+/WSl6ZbZtnl1MXfa9f5PtqYF6xr1tQYcxE+f3WsNDwf8f495yK8USM2rH/NTp8bGOFyjue6+YDGJ79riQ0XXA9AMcT2A8Bx+vyTipdv53OOeOJ+/fr1ENd5x+mJr7+cGXesXsBrrmISr/IBQ39jYpNtS1fzx6bGBS+btuaQczwzLld8rYPY1X7eR4FR4LYK1LOA84N9695mPs8Y93NlmTgrG3wSN8884oJh6+xyvvp65unPvDyS25advvTpI47z6AOOMTy3eacx75hnnr5dn/rqB5YXIsfoU4NjGiUPcgAT3okhH+bANwfGxa85pC3P6uN48tU37VLbjguxzV1/edLjY0zea9xaY/XFLhv6JI51/fbt20GnioOvvLBNfcmZ92yZJ/MVr4v3n//5n3+sHXVUA+3V0vlOQ3PubLocKvfMg2fmxaJP3ZiXEz15aiv3xDO+NvAHv2Kmzy2e7+47wm7AXDgWNoV1rC7wFA2R0wfbWkhxcjHwnPHB1DftXOxyAOvDhw/fP3369EMcY2SxxQODL5qLJDl//vz5cCiZF7bJTb3E0A78jKdd+sor44GDRjm2WqjY1riZRzcnv+lHgVHg/RWo5wSMPCs8y3insZ/z/NBuz1lhpmBwviSO51CeFzyDix32znEW8e6ZK4c868wJ/tUu42pHfJpYW/ngU/l7PnLu+/nQ5aQG9mLp4zg9/nxDxSZe2p6qUeooLr15qzFjxPv48eNf/vbOmPhU/fz8So5gaZf16PJJTmpDbxNfnsQ5thaMkzjg4VvXDGuD2tf6Gl+dmM81Ilfzxo7PbZt+1aeLZ45iiWGM5Gxuaaud+YqnZnJhrYJFLulvvOyP3UHkkbWoccFzrOqAX+aVsW/1fHcXYYrSiVILrPgWvBMsNy3zFUMf7PKAhEO+W0AXk34uKgsrp8rf8Vxw+mYccFf5G1Ms8xancmM+eaxwqyZVC+Ku8gezxpWPmsh7+lFgFLg/Beo5AcPVHvbs8RzrzhR967lg5oznueQ4WPlBih3viVPj61vPJ880eWqnv5g19z35iE1vM34984hTz/fqIxfHt3psMwbvezWqudc4FZv8GOPLXK2tujKetVQH542BXdbWcbBP0SfjmU+NJQewadqZg7FrreW44oOf+Xc2xEstjGOf3BlbxZN/zUt7+mypob7mrl3GNgfqUWNof6yvmvpe8arGyTVjHNMuba/1fHcXYUTJzW7itciKXxeG9vQVKxdE2lGwXNz1fStWFls7xrI5XrlWfvh0HBlj4eaXMVzYYGWrOF0s7Kuund0qBhxqrVKP5DPPo8AocH8K1HMChqv97lnh2dOdFfivxrfmPCMTO89kfDuujNOIqf3Kzrw8s6rdineOVx9ii4tdNnKRU47z3OFUG3Hz3E+8zFnfFa61qxxXftiBRQ76UCO+q0tPq7GMYQ1X2I5v6YNNzY/3Ve3ErH6uK7hmI3ZeXJlH52qXPtZDPXKu8ydG1i7xO3vw3qLhKtccNwd1zBy2nuWb+VjnxE8MfNTYuJ12tRaJcavnu7oIK1ZXJBeIQq7ET+Fy4zCehUk7CpEHTH13EdDXlkVccVqNV35ydMOoh4uJebGIS9NGXQ6DJVdt9ujacdK/xoBDHev85TT9KDAK3JcC3Zm42u+ewex7bfKDMZ+7s4bMV+dDYq/s8qytKoLrGd7lpH3GT7u9+aSPmPqCnW2L79YcGMRBz8TMHLHJXIy7wlXfxNOH3nni8kz96Pm84a/RyZG5rGvVQgw4ZKt2zmFnzRzL3s86OWEr9ipP/FOnxEjs6r/imD6rOmOTcdQhcwPfz3XsV/H0NU/jr+yxM44xch/mM/NbORgre+237iCZe/omZ/Pq1l+tRWLc6vmuLsIk3W1uxquQK/FTuIqVhUm7XEyM1/etWFnEld1qvPIjtouZPp/lKxZxaS7UusBqrl0s/Kuund0qBrY1bucv9+lHgVHgvhSo5wTsVvvds4KzZ2VzLLvV+VDPtc6u42o87PNCkB/c2sjZy1ziOQfOVksf7Va++dmgrX2H45x48nQ8c2TsFI2s3VZ+zMGZWnj5xc/fDsR8+tccjOFnk7yrnePYWTPHslcHYoKRtitM/LHX1nWFfbZamy08/ZKPY/b4e9Gt2NjkvO/dGn2Lhm/NwVyyr7yZU1Pr7Du22ZLPlnadXolzi+e7uwivRKkFWYmforEh8jDJwqQdMd04jNd3F2ceAthZXGOsOK3GKz8wM8+Or1hwTA6VW/Xdq2vHyTwzhmPyOJCZ/4wCo8BDKVDPCci7t3O/M+456J6nz3NzT+JgdheAej5151A9+4wnL/l6hspTu+pfc9+TT/UBe6VXzUke9JVLzq3wyC/1PkUj46lRxvMZvnyW/fLLL39855U5fBhjjvxtVQvrUHWvdvrv1ZuciZ3czafGkoO2Kzvmcx2uOMqV3rpkDZwHz/EuL/C9KOOziif/mtfKPmOtfOWYOahPznXPXdyqqe/YZqu+qVHa1Vrk3K2e7+4i3C02hc7iOVbFT+Gw95LKeC2MtrmYGKvv+rKQc4HWAq44rcYrv4wDV/2M6ULveLgJzanmulfXjpO+zNnglj8vxrh2lYs+048Co8B9KVDPGNi5j3O/M+75U8+jPGOPZQcm51f6yCHj8Zw24hI7LxRyzTOHsw+bvOis7NLG/Lq4xq/nKuNiJ3/G4Zr4Ytibi3o6Tg9W5qRtjq00Yjzjwo/v8HJeV44Z0zOd3xbBs42c8a2//71qoQ5Vv2onLjllPo5nb02y5s6rCfg04ydmN4Z9XR8rjsZKfHxTR/Gso+/0NNd35rCKJ99zNayaJP/MIfnLL8f0c87csh6OaWO++tYctcs42LC26l1CjFv1d3cRNnHEYuH4pejOK2oV33l6MHJB1cJoC3ZunvqunTHllD7YOF85rcYrPzDwrRvGePRfvnw55JR65OI031Wux3TtOLk5mbMR31iOySMPYeemHwVGgftUgL3sGcO50e13mLu/8+xhvJ4peX7VjD1f+NVgnBPG7TDr+SKWZ6S+1Q4szmbPwJWd85zP2bby6XxWesHj2FlYc1E7MZM7Z39+5qgltrURW18xsedr1YxZ9bTu1bfTws86Ymrf2cHBOoG/1cCpnLSv+nV28lcPbNAya7PiaBx69YFPjct7ttSfOMy7JrHbivdWDdM/c4Z/5iDfY+u05lrvIMarGnQ5drXgLJiLsNWY/mEUcDPVhf8wCQzRUWAUeBcFti4170Jogt61AqtL1nuQ9nPPC/57cLhGTPJ5tpxO1eluvyN8aiJjfxsFPAy6P3nfhsFEGQVGgUdVYC7Cj1q52/P2u4f38lnjZ98zXRr5g8Z7fzf29ivrrxHnIvxXTWZkFBgFRoFR4AoKzEX4CqI+IaQ/WpA/CvLeaT7jRfi9Nb2X+HMRvpdKDI9RYBQYBZ5cgbkIP3mBL5Qe36nMf6b4QrBvgpmL8Jvku2vnuQjfdXmG3CgwCowCo8AoMAqMAqPAtRSYi/C1lB3cUWAUGAVGgVFgFBgFRoG7VmAuwnddniE3CowCo8AoMAqMAqPAKHAtBeYifC1lB3cUGAVGgVFgFBgFRoFR4K4VmIvwXZdnyI0Co8AoMAqMAqPAKDAKXEuBuQhfS9nBHQVGgVFgFBgFRoFRYBS4awXmInzX5Rlyo8AoMAqMAqPAKDAKjALXUmAuwo2y/tvap/4Two/8OzL3/lOWe+0aWR9uyH/Z6F7+JaFj/yb8WwV+z9p2/y79W/MZ/+srMGvmfI33fl7stTufye08r32GXTOTc+8F53Ka31t8rnKn+139Iuy/EEO/p3mw/su//Mv3/LrlZWTPgmeRclHK9sgHlrofu/zvtUtdHvV5LsLXq9xvv/32A/hchH+Q42FebnkePNua2ft5sdfuGovGz+9jnwt7Y89FeK1UvVPMRXit1aVnrnoR9pDkQnvqRTjtxbnVvzl+7CK8+tB+zwPrrQtDjY8deHvt3srnHvznInz5KqwO99WeujyDQbykArc4D551zez9vNhrd8m6ijUXYZX4/v3YveBPy9OfuvNvte5PRx+PYwpc7SJsET98+PD9b3/725suwiTRLZRjyZ07f2zBr7i854F1bq767f1A22sn7iP3cxG+fPU8F9gr2VZ7Km3m+f4UuMV58KxrZu/nxV67+1sdf2U03xH+qyaMdOffat33CDP6FgWudhG2sPQ//fTTmy/C3YHrmD9CUT9c/dOs81zI8cnmYtOG7zp/+fLl8GMZcK+NGNra+91rD6zff//9kLPzHQ5jztOLUePxzhwafvv27QdcxvLHM6pdztd4OUcMtcQOHLlVzdIuuVb8zIc5cOiJK7Y26Vt5ZQyf5SAOPRi0Wp+Kt6VRzVu+dV3Jo/bpD6eqHXidDt3fdHgJN0c4gF8xk0PVpeaeOoNb5/XHzvgdN/PEjqZfck1ePle75KA22GQNO+0rTmdjzOm3FbDO1q6ur1dcM2rCOnetqw/vts7O+fq5gr9z+rNu2V/186KuZ+3AtG3tAWPjl/zd7853OYlvn/uSMd/pwROjOyfURxv51DW2N5e6FqtO8NvCkg+a4CuvygecqhH5re4FW1jEQid1M2ZyT3/n8ZMD8z5bQ+tDb42JMe08Ba5yEXbBUUCfKdae5kKu9i4k5mluCotvnFxgnz9/Piwg4zKXC6lbXMZnQYqtv33l4jj4fAf8559//uOCSh51o9UxY9acxTXX5NRxx4782LTYmiu4nW/yksPHjx9/OLDJqbNLbY7lI3bimBP4fNGsYXeoVi06rdCEmtvUKPFO1Qjd5Cfuqj+23tQha2HOGcOxyhu/1DB56JM4+TOVp6wBa0tf46mpcayjPh2P5Fn9nTMW+0cs9cpanxpP/On/qoC1yHU2a+bHS1Bq49pzParfp0+fDvuE/cmce6Dzdd9QDZ7r54Vrvtp1WO4T41WfPLvkymcTWMSh1XOhrhJi5Bkgv0udYWq6Jxc/z+Aoj8z5GJYapC5ggZHY2uWY8TJv7bI26Jl6ySnHxHIdwQG7tGFMfHPs/LRJDvhOO02Bq1yEKZyFcZNm0bcodsWuY2K6QMTrFpNz9OJgR6uLVlvGc8E7br+KUzcU9pWrHKoevOfGMxY98eBTfcRSB+0SR5vqu+IllvG1s57iqaHvFT/z6WzcwMmVmPjVA6FyqRyd7/paq1M0kvcp8ZKD/nu0ypyJV3UBl/G024rVzdUaWVvzq3ydT7+0cV5/Y1bNHae37p1Pt+ewU4tz4mXsef5RAfXM+mphneucPtZPO9e48+mXNs7rb7x7WjOuUdedHOnh7R7Urp7NuWbTF030rVjVLvcCeJ6/e/XrOKBx5brCk0+ti7XM+mLb5XZMv1XsGjM1l5cx1WkPlvVSS7FqTjUX7Rg3nvGznowZA840NafPVutTc8a2Yvme/OVe8TPWPB9X4OIX4VpQF2jdOCtqFpYF51fdUNrU4nfj2IhjLxcWYy4qOelT8XO+bgDmOjwXb26MzpdY3Ti4qzmxzaHjvfKVr9p22plvbtpqt8LP8eqTuHJ3LP0cs9+a04beA8t60+NLo893xzrtXbvW7gBw5D/iZ2zX20qHzMuadjHB6XhCSa7dfOJX+lu1xZb5rBEcjq2ZVZ7grfJbcXxrvJrvvP+pgLWo+wGLVT2Ye/Y1oy7dHkQX9dIu94djna/7wvOg7i0rs2XnHDyy1fEOu9rgv8WX+boOOoxqt4WZZ9gKq453uRBTOzB93tJlxcuz81hdsvbEX/HK8aoffjRieY7y3tl1fFO/DucAPv85WYGLXoTrgoJNN7bF0gXtosSWZw8f3l2QednIZ+ZdRHkxSGzn8xCTl/j0XWM8cbXJDeCYcZijmUvy9bnDxGcVj7mM2dnVjXMg8c//4OtmVJsuZzBWdnvyWWEnd3kRHz1WPFYa4e9akytjFY/3irHSSDxrJ8eut86Jbd7g03yvuSWnrZgrnvLR1/VknC2/Y2sguREHe/Vgzlhdb3z50auTGM7VOI7D3XqeE0+c6XsFrIf1c62+8ppRk7pGUTD3cGfnHtzyVWNsus8fMTq7vXugw07urgZz6HhgU/dlh1Ht5N9pkOvqLbkQ0zhg7sEy18orcbTp9DAGvXbum9rrj21+Jqg7nD3Xqn7aGCP5dlxzXt/pT1PgohdhF0pdFL53C6LSdaN5CDBfF8RqcSWWXOhtFZsF5ILVhr7zrfNdLh1e5V43QOKunlf5im0OnV03Zhz4uhnVBvvatuz25LPC7vQiPuul47GVC5zhUutS8TqMbgw8Dx14Hms1Dvbm7Vr2HdtsGd+adjG7/BLHZzGsbeJrY79VW2zEIjZ68DOG5EHbwhW/9uLV/FZYxN2TR40z76crQE3cP6t6gPrsa2a1RskdXTyfOrtuzEq4/z0P0NGzWxv6LbutuiRGhy0uGDb5djywqfE6jGonJhxqyzOsYldb37tcmJMLmHuwVrw854/VhRhbtZdv9itexPJcw76zW/FVj69fvx5+xhwdpr1NgYtehDsqdZF1NjmWizvHKb4LZw9mt7Aqdm7KjMW4Cz7Hfe6wmXOBsoBtdTHLAYy9DVv4uFH1E8vxjle10VcN4UzTzvdjdvLXz3f9sl/ZdHqZa4cnjvlmDJ4Zd404V/F498NemxWu41UT/bLfgyteza36Eq/mQSzGK/fkkM+Jadyq22oNVH748UHJ/zWdH5j6V9zkUZ/rfnA++TpGnzU9J15izfO2Aq4TauFzra01cE9o90xrxjW62oOOa6cWqrvav2iZ+3e1nzs7953617oY2x5sfRzramUO1Vafui87DGyr3UqDzPmUXFI3uaVOe7DMFQ7Zqm/iph3jeS/g3bWQdvlcdXGu+nZ2K77UgP/Jkv9Jc1U340y/T4F3uQizEHNBJVU3GgslGwslfeqiTFueK46LPS+UjuViwo/fnMDGI2bXKrY25JVYjHeLOQ8Dfbd6c8/DQNzciN1mArdq1fmaU2qMb+WqXWpTbWounY/YVS9zTfzEM5e6PrCpvsbNnLBJHcWuOaARBw0HDnM08XzXN+fk5drK9aZ/za1y0i7jYAMXvpivjV/BxJcN31wb6mbsrTWgjVjE8/82Nz/nKq7jW33lhm3VQH/wt/LQbvrTFWCN8isZbWide6PW9lXWjHmyd+sezP2sXdqgpXs/zzbWd/pihx9jadftfezSptbF+mVffZgTO/e3OSR+4tR92WFgv7JLbbCpZ9jeXPbodAzLXJMT3K0X/vmempB3vRfol3YHgPhP1cUpYuW5pq5ywG7F1/G6nsw/MYw3/bYCD3MR7hadi4cF4VcuShah4/R+RysXSi4qbFic/r5e/FfNRYePdt3hI37dfJUbONXG2NjyAcVfhZAftnxlrthqhy611XgrX+zQwBi5WcFUc+yyVfzMZ+XT6SVOxT8WS/usC5oxTg7O0+eHfeKmL/yxhaN1YX7lCw726kZf19tKh46T61086rX1V2GVe8ez8qtrYMXPNdxhkrd+cqWv2Klz5qZdpwE+5LVag3vjZex5/lOBuh7Qk7Fs1cZ6aWPtq98jrxm5s+9r/pln2qmHvXO5Rle+de/ynq07J9U98bM2Wz4dj/TN2NjmvjduYmBf7RjLfQ5PYnRnmJjHcsEXLtpVnYi5hWVNJS0ZgwAAHPVJREFUPM/NU56Jp62xOINW9wLwtLNXn04X4hKrnmuMpb8cKt9j/pmHOU6/rcDVL8Lb4Wd2jwKrzbTHd2wupwAHUncoXS7CII0Co8B7K7B1AXlvbq8YnzN3dVF/RT26i/sr6nDJnOcifEk1r4Q1F+ErCXsCLN9pWP1YwgkwYzoKjAJ3rsBchO+rQHMR/rMers363eQ/LebpHAXmInyOajf2mYvwjQWfcKPAKPCyCnjZmL/9uY8lMBfh/68D9wB+dCJ/VOU+KvT4LOYi/AA1nIvwAxRpKI4Co8BTKDAX4fsq41yE/78e/EjEr7/+el/FeRI2cxF+kkJOGqPAKDAKjAKjwCgwCowCpykwF+HT9BrrUWAUGAVGgVFgFBgFRoEnUWAuwk9SyEljFBgFRoFRYBQYBUaBUeA0BeYifJpeYz0KjAKjwCgwCowCo8Ao8CQKzEX4SQo5aYwCo8AoMAqMAqPAKDAKnKbAXIRP02usR4FRYBQYBUaBUWAUGAWeRIG5CD9JISeNUWAUGAVGgVFgFBgFRoHTFHjJi/De3xO51+40yd/H2lwe9Z+q9JeJ09+iqdf8Uv1bqD0xXlUB/7nYU/fZrX+3+q3Pn/daD+fW41p8/+M//uPkf0DCs/tRP+uupeXgrhWYi/Bam+9uqFMP6Q3Ik6Y4BPiXZC5x+TOXRz0crv1BhD58CNjU671qL4/pR4EtBdwXnBP5tffMYH2nH8+3/Jer9l68fvvttx9kIL9b8lTnvbpKlvw4Sx6l7a3HrfK5xEXYnB71s+9WWr9ynLkIb1T/vS9DcxH+szjnfhD9ibB+6j5U37v2a7YzMwr8qQBnxFs+4LkI//TTTz/8IdDL8amXvj9Z7X/ykrL6A+dqH3Z7dn/U0y3POX+oTdX29Mi39ThWj9uy+f59LsK3Vvw1481FeKPuq0N4w+Vup8zlLR+a75ncOR9Ee/l2H6rqtfqA3os9dqPANRVgfb5ljeJbL2u3XPvHLl4rLt2evabO55w/cxF+e0UucRF+O4tBeHYF7u4i7AH39evXw3c6/Gu7+tdg1S7nPTz1pWdD2ZznQ+Af//jH4a/YtF3Z6UtfffKDyIMdHMbF9QLqvOPksWrmSDwamHxoOS5GxhcLG+fpv3z5ctBTHtrtzYXYiZc6iVVjpo15M5a6ZN3EsT7GgzP8eSdGti0sYh3TK/2Nh58cmPe5XhjggW3HKznO8yhwLQVYn6zBcxv+3bpmvJ4VjLlH6r6t5wh2HS/3C/NgsJ+JD3ZtHaZc8ZND8tqD09lkbPe7uXbnj+eZNvTiVn9tPLuSL3PmlBzqcxdPfY/hYUeMb9++HfqMd0o9Kife059crIm21sk6q0VdW9jXHMkL/Ioptj3Y4tLXzzrrYX26WDVG5QIuXDos8Fyr2NiqNhl/a676u24cN5Z4ckoNkgd+2FbNzVEc3/GVX8WRw7P1d3cRtsguPAWnWLlYsfvw4cP3T58+HTaBcxYzi+5GseAuHP15p2ln8bXTL21cnMbTRp/krw2c+OKdVnM6DMZ/iGFeDMsvx9RLzmmXY8SCU6fLnlw6v8TneYtX6qJWcOU5D2btcswc4S9X7ZJX5XCKXskdXuLLVQ6ZszbJAd9po8AtFHD95Zo8NW7df/iL69r3Pdd53Wt844I9YnPvuV8Zx6fbw4wZS397Y9d5cNmznOHG6PZo5eFZXPFqvGPnD7HI2dbFJt/EwZZ8Pn/+rNsfWqe2f0z+80HsjvMePDSABzHQWk7n1KNyIxc42OAoPmNyz7p3NXAsdbB29Ww2Fr025GKDA/HEqmvId+fxy59Bl/NKb/zqnD7ykBc9jZh+7m/NmYM+xEqejBNDTbZ0S448Vxx9tVMX7lTgo6H5JK9nfL7bi7DFUXSLZjFdeC4I7fDLjeh4Lh4L3tnhL6Z2cpGD72KzsKuPPLUhfh4GjJvDarElLvZ1A4mdOa84Oi4v3/fkckynVR7kpa9aGl/u1TfrpA191a+zM4Y57dEL7KozYxXL9+Qvd/ynjQK3VsA9zLnil2t/L5c8O/SpY3v2mr727hf5uFfAyua4djnHc8Vxfs/eVp+K3e13cbtcmWO8nt/62BMnzwd8PP+06fotPuafuB1GjlU8tUou6n5qPTJO9ywuMWm+1zi8+5mJHdolP7EZTzvH6Vf1dVzN1NB14HzlBKa2+ma8nBfL+Zon2F0+2G/NiWdfdZKf8em7ONUPu5qTOoglNusc/1dqd3sRdiNlMbLodeFhZyEtbPqm/ZadhwZ9tROjcsvx6iMHfOqGdiGuFl31qe9i4+9mSC7O08vLzbCyy3F9Oj3h4gfDileOr7CqBsSSY/LPeIyv7HI84ydW6sV4Z9fxxS9rWHEyxjyPArdWwL3rWbAnPvvFS7Q96zpb7qmtcfeyOPTu5W6PgaUPMbrW7UPsVni5J9UD22yrcWxWuYJBPoklt8w3tU8uGZ9n5tKvYmu/xVWbY3gdd8byLBPrWD20y178zMc1tOKf8dWxWwPgdDyJv8IWz7Xnu/i+d5qvMM1XX7Ec18+81UQO2tFvzaUdzxXXdzBWXDq/bl3XWovXca68nu39oS7CLDIPmlwQFqUW1nF67cGw4HUxp1230FzAueHzufORA3N1Q2/xxa/61HexUxdsug1uzi5y7ZJ/PjOvzzGdiJ+++WzOKyw1yLrI0fzUAtzklXHyWX9sjZ9YqZfY1a7j23HttMlY8zwK3FIB9zVrfE9j/XqmYu8adw+5D3J/5bN2ngHG1S/n6x7LeKt9JE6d37O31SL55jPz2Ywl55wTSx/fk1fVsp4zmW9qLpbYW3Fzbi8euFV7uNWxxMu8akzf1Stx8nMWO99rbsnJNdfFXPEEGwzqWbHlZR19T3zHXA+u2xVmzTmxMk9xkh8xst7H5oxlTyxzAV+sLd3UXT6JIW71V5Oam/bP3D/URZgCuQgsdG6CrUJqz8LYssuNUO2Yy03fLYzqo03nWxeitvbVp75rl5vDPLHNJi831Aqr8+k2Bv4eQhk//fPZ+BVLDbY2LDgZb4WV8fTp6lX5dlqsYsAfDfn5QH4+Eb2njQL3okDdT8d45Zmqbe6H1T7Qlt6Yubf1O3bedL6JLU5iM58c0z739som7euz+5u42cDyvJOTuWlXtUwu2jBWz6TE1s5+dZ47vwev06EbA/NYPYxL3/GWL7xovmObLeOrZ60x9l1+4qywxbM+vnf4YDFuTVaYxlxh6Wfe2tM718XfmhNDrfwFAsZYccmY2hJbPcSttd7C0+dZ+7u9CNdFU4vmAqobDD8vy1m03FAWvLNLf+3kIgcXV+L7XH0cdzHD2yae+I7bV5/6rh18zGWF6bibwfc9uYhtPPrUaVWLtF/pUnlkndKfcT+IGM+c0y6f9+iFfWe34kuu/k+Wapkx53kUeE8FWMu5T45xyX2srfvZs+HYXqt7GBz3j3ukYtZYqzNQnDrf7Vkwk2vHy7irHn8vRWnDuLquOFUtk4tY3dhWzcyh5n8KXqfVufUwLv0eXONgm636Vu20ZbyrB/MrbRx37a3qZYzkqO9Kb7HEFoN8WB/Ut2vgVR/ttuawMSb/E1v95gu+3eczPFK3zs68mcs4vsvvFfq7vQh76FgEipOFtYh1g7mQc9HVRerCIkYWfWWXNiywyk2O9GKnD+NgJ3/G5Fptxas+9V27erh2HInx8ePHHzZjZycmvbkc0wlb8Gt+HVbNVQ3gQvM960et4Q4+GqzsDhPxn716uZbkAIS5V76Oo0naq2WOBZV5HAUurgC/Dov9YnMd5945ti5Z3/WD1DUuTrcnjUlf7RkDlz0ihmN5RuDnh3vdZ4nfcdy7t83fcyNxu+cu1+78qZyMk1oSs35W1DFrVu2Smz6dRs7R0zo85lJ3scHL8a4e4nWxnfPMU7s8G7WRn7ErJ+0yDjZc/OrlTwx6dU98MPKzzvUpNjzZOzYwUgewyEF77exrzC5vvntLXJrz4m3NGaP2xsz9lNg5Ln98bHVMTTJPx+Sp7yv0d3sRpnAUhELxlQcMhXHjYFebBdWXPu1cmCyUjFHtxKkLw9iJ70Jc+RA/Nxuc5VHxzaf61HftyKPqg23yw4Yveeq7N5eKx3tt1Yb45rbSRQ3gZtNW/uTm78CscWv98NGGvmpOjE4vxoyHnxzkL7dj/plH+szzKHBJBVyfrln7uv5c13VcLqzvenYwp597ibGtveY+lge2YNTzRlztwMeWr1VLbPFO2dtbZ1wXs2rbnT/VBl78/tqqpZrlOZQaME4u+KXWlVeXAzi0Y3grraovNcE26wF2cq+8sLeW9P4OX7nJu+bWcco6g4Wme34ErXIgNl+uFWvlGqv25p25yTtzMyfsrCvzWUNsjJe+lUs3l/Hrs3yqjth18To7uGVca6Uu4vheOTzz+11fhJ9Z+EfI7ZU3xqo+HtZ5KK5sZ3wUGAVGgUdWgEvRK16M7q1m1MDL9L1xewY+cxF+hipeKYe5CP8orHrU7/r8aDVvo8AoMAo8vgJ8F3LrxxIeP8PHyMDv5Hbf5X2MDO6f5VyE779G78bQi998R+DP/0N6668J361QE3gUGAVGgVHgqRTwbx/5cYb5G8jrlnYuwtfV96HR5yL8Z/k4lH799dc/B+ZpFBgFRoFRYBS4ogJ85vDZM+26CtzdRfi66Q76KDAKjAKjwCgwCowCo8Ao8P8KzEV4VsIoMAqMAqPAKDAKjAKjwEsqMBfhlyz7JD0KjAKjwCgwCowCo8AoMBfhWQOjwCgwCowCo8AoMAqMAi+pwFyEX7Lsk/QoMAqMAqPAKDAKjAKjwFyEZw2MAqPAKDAKjAKjwCgwCrykAnMRfsmyT9KjwCgwCowCo8AoMAqMAg95EeZfWHmEf9hg698Hv8bS8xdwP/s/gOHvN76Xf3KS9cgvPT/1X/7hl6Q/wjq+xlodzFFgFBgFRoFR4B4UuMpF2H8SkMuBX6d84HvR0Zc+/e/1IsxFFO62R7kIw/mRfmm36+OZLsLmNP98s7tn+lFgnwJ+3pz6B9F96GM1CowCz67AVS7CfEfy3O9K+l3Nesn57bff/qjFPV6EOYzrJeYRLsL3qOUfhV48eGmsa2RhfvVhNOQPa6d+EOd3hM2prqGrk58Ao8CDKzAX4Qcv4NAfBd5ZgYtfhP1A53A6p+25mO2xOSf2W3zmIvwW9U7zdY0900X4NAXGehQYBUaBUWAUGAUuocDVLsKnfnfMZPK7ZI7VPi/CfOfZH6Go34X2OwXO549XgCnO169fv3Opynm/m6tvxZaTlzLt7MEWg+fk0l3gKs6e7wwmJtyJg19yTX3glrh1jnkwaYnNeGpj7l1fMc31GN5WLZhTV/ovX74c6iV2xyPHrENimCd2/i0EY8m/y7nWCQ7wARueq2YMORCHeBmDsZpT8sE3eROrzuvfYcmBOVvVJtfH1pz+1qbyMpZ8Oq7Jg3nXAHGzYScv9WfM2BUnfed5rcAxLdHV9ZrrFMS6Nrq1WW2soYysnzG6eeJix5x2uabAquuGtYi94/p166RyxIavGkPO048Co8DzKXDxi7AfgBxC5zQPpnooJpYH3IcPHw6HHXP65Qfy58+ff/iZXQ64xMUHjE+fPh0OWQ978Dk8zcGcuoNUXh6+2Nrk9PHjxz8uMB1WN1a5imlPvOTohxpj8mQMDWza5CGvlnDNdky7tOVZ7NQ3bY7hHatF1pX8yDPzyFj1mT/oZH61vnJP7cCoNdAuc7TGWYsa3/omXzm45oyXNuSc8+DAgdZxybhwTyzm5OH6qO/Y+CNIW3MZh+eqE2PmR99xVbfkiG3ma5yKb27UodZMn+n3KdBpab2yNnUtHttTx9bP6vzK+rtGcm91uHXduPY6rDxHtMsx9CBe5r5PybEaBUaBR1Xg4hfhPLw4UPjKg2aPUImRh5m+HmD02eoHZs7xLK5+vmeM7qDFF5+0q9jkmBekjFfz5z2xOt7yqL5buOYD3qrVPOr7yk9stat2Nac6X98rnu+pixrUfBw/98PKD3pxfa94crIGqxwZzw/rmmtXX2wYz3x5Tw71PXFXXLTpfNWNOZr5dTXdmjOGPf41/4y/4lr9eE89xAcr9xbvxDMP7aY/XYFOy65e7pGV5nV+a/04R5xsq/VZ7Sq/um7qujIG3F1Hla82csh96Nz0o8Ao8JwKXPwiXGXyUDrnYPHArB969eAzJgekB51jxgfDLw9W8X3HxzH8sq3Gtelir3yS/+pAXo0TL/2NT+8hXj+s4Gbu9ua3wjKO9vaplbG3uGpzDE+tEt8xuYplvFPWlNqYB73+4lXd9JET8/rIJfOqPJlbYTMHbl78Kj7z8Ky8tjDlVbEYNx/xfE8O+m/NaWOvbcU9plv1W61FcHNf13d5TH+6Ap2WjHXrvI5bv25POdetrVWdYZ98Vvu/+h97VxXWo+tohe3e6vIXZ/pRYBR4LgWufhFGLj/QObDOadW/Hnxi5kHngZYHsYcfdjTfkxfPebDX57Q1Ln3GdrzDZy75+4FR4/jOB0NtxMq8nBdLH989/I0NtnkkF3H2aKctvXGMm3M878HrtIJbchVXvL0fVugFjnWv/r5X/uaFnzZdzBXPY9rUOhK/4ssd/s7Jq/JVH/oOq/NzDPyq9dZcxuIZnq6zXFNbuolvHumX+MyLvcot7ed5vwJ1nVgv10PtXYOuS3qafs4zZn3FoL40fLrzi7msdXcmYFPXybH3Q9Bmjdb1jl2Xh/7TjwKjwHMqcJOL8OpA2yupB+qxD8z6YVwPOnl4ePvuAQ2feqju5Zix9enwawxzk5O+W/2Ko1jqBGb9wME3demwqg1czKXj6YeHcSv3PXjiY2vrxpgzXn7o6lP7qknnL17lr685M9/F7PKTxwqb+VqfFT62xsBnC9O4HZb51DzxETMvnGJtzWmTtQI/Y3Rc8Kt8yLGuV+zwT14rPLlMv1+BqqW1ZnzVat2w06/bH85Zw1Wdwcla55pKLtX/2Lu+7J3kkOegNnLt8tBm+lFgFHguBW5yEa4f+KdK6IEIDq0efOLVg65+qFYc38Gzecgby/FjfcbWtsNnrvKvH0b6r3pxK0fH/RDrOBE7PwAql44fY2LXmHLMDzDH7LsYFc93bG3Wwnzq+J4PKzGSd/2w830VR1/6uqbgxHhqKk/7lTaMJx7vq5wqxxXmVkw1xrdrXZ2025rTRv5cNrKOK92wSd3qO7jm7QWGMeMwN+1tCnRaUq/Uu0bYs6eqT64f1yFxsonr+tQu1xL2ibXn3RiZV42ljeOrfajd9KPAKPA8Clz8Isz/TZwfUH64ebghHc/5AZhy8tsFOABt3QdhPQi1zYPOQ9TD1gOOuI5pUw9a5lf8jFV780ysFX7lr11qVPHrO7Z5iUInfvsFvwVDnMrJOJmbY2pCnDrWaVf5aNN9gO7B0yb1I0ZXC/LjN3H4YdWtEfk5py3j+KOBY9qom77mpDa+64cdvOFCLSp3ccwt8bGlVnwxT2M+sRNPjMql0xssfHOtmyNj8vj999+/82VjXLytOe1rb0wxnDd2jpuPXLDt9LX+6Vt1Ms70pyvQadnVIZGtZ65VcHJPHVs/1tU1LmbW2TWijRx4z7Pv2Lt+xEx8OdDT5JB5yCFzFW/6UWAUeA4FLnoR9gDlIMmvepB5aNbxPIjSvx5C9eCzFPWgwy5x/P2zHnwecpUHeM6lf+VhXHvz8pAWo+J3/LvcxRG/9h7kcgQXDnzZ0sbLGh8GySltHKcXl75qJ372XQ5qdgxvpRX41Re+fImtL2Ndq+sSfdJf3qkbOPolrrZqg5bfvn07fMCq3R4OcOcPjauLsLGNQ1/5VS7YqAkc4J3+1lCcOp/rbWuuy2+lV9oSN/mkrtpZS+3wwS4vMIxlnvpOf7oCW1rWelET13hdn9bJuuxZP3Vf62sWrgVjOs57rtVj7/rVdcR48gSTPQkP8qHJoXITc/pRYBR4fAUuehF+fDkmg0dUgA/CvCg9Yg7PwLm7aDxDXpPD6yjgHy69CL9O5pPpKPC6CsxF+HVr/xSZ+8HFJWza+ynAH0b4juHU4f1qMJHfroDfAWY9TxsFRoHXUGAuwq9R58lyFLiKAv5BhEvwfBftKhIP6JUUqD/H7I97zI9BXEnwgR0F7lSBuQjfaWGG1ijwKArU/8H1UXgPz9dWIH8+OH8m/bVVmexHgddTYC7Cr1fzyXgUGAVGgVFgFBgFRoFR4Pv373MRnmUwCowCo8AoMAqMAqPAKPCSCsxF+CXLPkmPAqPAKDAKjAKjwCgwCsxFeNbAKDAKjAKjwCgwCowCo8BLKjAX4Zcs+yQ9CowCo8AoMAqMAqPAKDAX4VkDo8AoMAqMAqPAKDAKjAIvqcBchF+y7JP0KDAKjAKjwCgwCowCo8BchGcNjAKjwCgwCowCo8AoMAq8pAJzEb5C2edfKLqCqAM5CowCo8AoMAqMAqPAhRWYi/CFBQVuLsJXEHUgR4FRYBQYBUaBUWAUuLACcxG+sKADNwqMAqPAKDAKjAKjwCjwGArc3UX473//+/e//e1v379+/fr9X//1Xw/P//jHPw5q/u///u9hzH8X/qeffjp891Wp678dD46+K5t/+7d/c+rQ8y4+fc4bn7EaC962tGMs37f89AcrOfzyyy+HvJOLttOPAqPAKDAKjAKjwCgwCpynwN1dhLm4fvjw4funT58Ol0Evs/64QV4Gec7L8OfPnw+XTqWo814wvbRyQQWX5mU18eBCfC7kzNPA5JKaY1xu5ZlYlesxP3y9KCdHYtVL+YHM/GcUGAVGgVFgFBgFRoFR4GwF7vIizKUyL5ZkVy+1jHk55vLYNS+yXiqxy4tu+tTLrHP18rzFw4uvl2rfwdrjt8rHPBJPftOPAqPAKDAKjAKjwCgwCpynwN1ehPNy210sSbcb9+KaP1oglnP53Vxl45LZjXs59RLa2VUe9Z0Ye/zgV/8AgG/lIOfpR4FRYBQYBUaBUWAUGAXOV+BuL8JcCm1eBPNym89cMr185kXS76R6EQbPyzD+fndY3/e+CK++K23+XsbVZfpRYBQYBUaBUWAUGAVGgfMVeKiLcF5oa8pecPMC3V2E9XPOy2X3HVts6yW0s/MiLVZ9B2eP31yErc70o8AoMAqMAqPAKDAKXF+Bh7gII0N3kUx5uADnd4OZ87K7ukAn5uoSWi/Y6WP8evGt7yv+1W7F13FiTxsFRoFRYBQYBUaBUWAUuIwCD3MRPnYZdN5Lr9/J5UcgHONXsnH5pDnv5dJLqT8ugY2Y2jB2zYuw+HD2O9vyZEwe9GmD37RRYBQYBUaBUWAUGAVGgdMUeJiLMGl5WeUS6Fd+F9jv3jr35cuXw/8Ax0W48+1+JthLphheopX12hdh4iQHLubfvn07/DyzXJz3siy36UeBUWAUGAVGgVFgFBgF9itwdxfh/dRfx9LvCnsRfp3MJ9NRYBQYBUaBUWAUGAWup8BchK+n7cWQ+c5vfuf7YsADNAqMAqPAKDAKjAKjwAsrMBfhOys+PwbBd4Bt3c8pOzf9KDAKjAKjwCgwCowCo8D5CsxF+HztruLpz//6M8r08yMRV5F6QEeBUWAUGAVGgVHgxRWYi/CLL4BJfxQYBUaBUWAUGAVGgVdVYC7Cr1r5yXsUGAVGgVFgFBgFRoEXV2Auwi++ACb9UWAUGAVGgVFgFBgFXlWBuQi/auUn71FgFBgFRoFRYBQYBV5cgbkIv/gCmPRHgVFgFBgFRoFRYBR4VQXmIvyqlZ+8R4FRYBQYBUaBUWAUeHEF5iL84gtg0h8FRoFRYBQYBUaBUeBVFZiL8KtWfvIeBUaBUWAUGAVGgVHgxRWYi/CLL4BJfxQYBUaBUWAUGAVGgVdVYC7Cr1r5yXsUGAVGgVFgFBgFRoEXV2Auwi++ACb9UWAUGAVGgVFgFBgFXlWB/wMv25df5UDLaAAAAABJRU5ErkJggg==[/img]
Elena wonders whether she could play the Info Gap with area included as an extra piece of information in the data cards. She draws a card with this information and asks Han to play.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAANgAAACyCAYAAAAgTwHRAAAfr0lEQVR4Ae2dC/QWRfnHUTvmLfOWpMcEtaMhmRjlJU3LvKZlHEkLTIG0NDNCw8Qr4iXLu2KGmGUigaahqGkqEoF4Owaloqbk3RK8FyoB8z+f6f/8nN/8Zvfd3Xf3fXf3fZ5z9uzu7MwzM995vjOzs7MzvYxKqRB4/fXXzdixY22apk6dagYMGGBeffXVUqVRE5McgV7JvarPViBw2mmnmV69epkVK1bY6Pr372+uvfbaVkStcRSAgBKsAFCbVblgwYIuFV/4wheUYF1oVO9CCVbiMps+fbrZaaedzGuvvVbiVGrS4hDoQbBx48bZLgrnqsrs2bNtHuhquQfuSWTSpEk2HOd2yfLly83AgQPNjBkz2pUEjTcHBLoRbPHixWbvvfc2kIsz91UUiPHd737XLFmyJHXyH3/8cbPtttu2lWCQa/DgwZZcvIudcsopqfOhAcqBQDeCUcNDLM4YWdIavxxZeT8VVBBZWmAICTH32msvm/92tWAjR440d9xxh5kyZYqZOHGiOfXUU9/PnF5VCoFuBMMoMTBaLs6+kUoLh+Fx0P0SIxTjlC6Z3wKKf3kOgWktihDSLelKo9+tWEh/Ix2Ch+RJ8BB3wpMWeS6tqjwXd7ciY2he3OV8ww03pMmG+i0RAl0Ek0IXo+Lsk0RINHr06G7dKAnrEpJrN/y0adO6ddn853lhImmUfCTV6+ZBruN0SFfSzbPEJWmAIKJDdEIyqcTwT3i3sqFLSBfRPWTIXvTruToIdBFMam9pVcSA3No1ZDhiJC6ZcBODEgPzIQnpFz8SVmrwqLObtriwIRKIfznjx29hotIuOIh/0SHnqOfoIy9uugWHqLhEp56riUAXwVwDIytiJK5xiptrWOLm+osKj2H5ZCnasMSA/QrALS7S5bYiQvCotIlOlyiuvihM/HgI0yguV69eVw8BSzApZN/4uXcNM2Q4cWEJD/EknGvEYqRRRpwnlELsUFySfvdZyM1Nj+jLk2B+BeXGp9fVRcASLFSzkiUhgRiSEMU1hkbGiJ6QQYpu17AFRtEZIrzrJumScFFn0ReKS9Lm6nWv3UpB9Evao+IP4URY/Pv6JG0uphKPnquPgCUYhet2+yRbvqH49+IvKrw8DxmWGGnI6CVcXmchURQh/HjE6KPSJs+jSBGFUwiHRrr8tOl9tRDoJQUcZUy4S60bZThCliiDk+cSh8RJSyFuecH2xBNPdPtALnG7FQhxxsUt6YtLm5A2lOconJRgeZVydfT0woiEQKFki4FiSFGGQzh5FtW9EoOU53/84x9tqxlnxKH0xLmF0hAiUh4EIx2CjeRJ4pJ0+ORTgsWVXj2fdY0i1jN7mitFoL0IKMHai7/GXnMElGA1L2DNXnsRUIK1F3+NveYIKMFqXsCavfYioARrL/4ae80RUILVvIA1e+1FQAnWXvw19pojoASreQFr9tqLgBKsvfhr7DVHQAlW8wLW7LUXASVYe/HX2GuOgBKs5gWs2WsvAkqwJvGXzRpY4rpv376G87BhwwzuKoqAEqwJG/jLX/5i1llnHdOnTx/Dpg2///3v7Xm33XZTgjWBa52CKsEylibk4v+vww47LKMGDdYJCCjBMpYyrRRHUrnrrrvM0KFD7SJCF110UdJg6q/iCCjBMhSgtF50CZPIPffc02O5OpbHVqk/AkqwDGUMOT784Q8nDsmgh7usANcrr7yyee+99xLrUI/VREAJlqHc0nYPDzjggB4Eg2SLFi3KELsGqRICSrAMpZWWYBMmTOhBsO222y5DzBqkaggowTKUWFqCPfXUU5Zgq6yyShfRNtpoI/P0009niF2DVAkBJViG0uIdjO9fST8mH3jggWbDDTe0hGI7WDY1p4sIUXXnlAwFUKEgSrAMhfWPf/zDDnIMGDDAcC3CaKF7j/stt9xiyXTuueeKN3seO3asdR8+fHg3d72pFwJKsIzlCZmYweGPDjKE70r//v3Njjvu6Dp1XfNdjPBnnHFGl5te1AsBJViT5QmhIBuHL+eff74lUNwOlTvssIP1Q7dRpX4IKMEKKlPetRjUGDJkSGwML7/8sllvvfXMqquuaubOnRvrVx9WDwElWEFldsQRR1jS+F3GUHSzZs2yrdgnPvEJ869//SvkRd0qioASrICCoyXi3erkk09OrP2Xv/ylDfPlL385cRj1WH4ElGAFlNGuu+5q+vXrZ958881U2k844QRLsu9///upwqnn8iKgBMu5bH71q19Zklx11VWZNPPNjNbvwgsvzBReA5ULASVYjuXBR2M+KO+3335NaWW/Nkh20003NaVHA7cfASVYjmUgXbyZM2c2pZWP1WussYYdXfzb3/7WlC4N3F4ElGA54c/WtbQ6xxxzTC4a2QEUfZ/5zGfMW2+9lYtOVdJ6BJRgOWH+ta99zWy88cbm+eefz0mjMZdddpkl2UEHHZSbTlXUWgSUYDngffPNN1siFDEw8cMf/tDqpvupUj0ElGA5lBkfiHfZZZccNIVVMGhCd/GKK64Ie1DX0iKgBGuyaH72s59Z46cVK0qWLFlittpqKxsPi+eoVAcBJVgTZcW0ppVWWqklS7ctWLDAruOx6aab6o+aTZRZq4MqwZpA/Nvf/rZZffXVzSOPPNKEluRB5V2P1YP/+9//Jg+oPtuGgBIsI/SzZ8+2XbbTTz89o4ZsweQXmBEjRmRToKFaioASLCPcO++8s9lmm20M70etFlYTZtDjzDPPbHXUGl9KBJRgKQHDu8x8v+aaazKEbi7IQw89ZI477jjz6U9/2pJs8uTJzSnU0IUioARLCS+Lha6//vqGD8utlLfffttAaLqkjz/+uOGHTpYs+OAHP2juu+++ViZF40qBgBIsBVh4HT16tG05xowZY5577rmUobN5Z9rUqFGjzI033thtFaqHH37YpmXrrbc2L730UjblGqpQBJRgKeB99NFHrUEfe+yxBqM//vjjzZVXXmlblBRqEnllSbhbb73VMIODLmnUFKzrrrvOpmn//fdPpFc9tRYBJVgKvL/yla+YTTbZxLCOBrJ8+XK72M1ZZ51lxo0bZ6ZPn95j2bYU6s3ixYvNn//8ZzsHkbUXf/vb30YSy9VL/Ax6/OAHP3Cd9boECCjBEhYCO6lgxOPHjw+GYJVeunCM7DEIgT/uGc7nOxm/oLzwwgvmxRdfNM8884x57LHH7CI3kHLixInmlFNOMT/+8Y8NP2w++OCDZtmyZcF4ohxlgwndGikKofa4K8ES4r7llluaL37xi4l8s1TAX//6V3P77bfbgYlLL73U/PSnP7Xkg4DnnHOOueSSS8yvf/1r2+pBKGkVE0UQ4Yn5kFQCRU7biohanSMQUIJFAOM6QwgM97bbbnOdS3dN69i7d287yjl//vzSpa8TE6QEa1DqdOsgF9OiqiBz5syx6f3sZz+beO38KuSrqmlUgjUoOd5t1lxzzUJGChtEnfnxb37zG0uygw8+OLMODZgPAkqwGBxZW4PWi1G6qgmDJqT9xBNPrFrSa5VeJVhMcbJpAzuoLF26NMZXeR9985vftCTjW51KexBQgkXgzt/DtAB8i8pTGK6nZfS3OcozDtHFLy0smkM+9EdNQaW1ZyVYAO9///vfZt111zWDBw8OPO3uhPFGHWywJ8LMDP7jcv3yfucK69jzgZnjtNNOcx9lvmZ3TTZsZ97ik08+mVmPBsyGgBIsgBsfiiHC/fffH3ja3Um2LvLPGDS/lYhwjaHLZhD4594lkusff3ktonP33Xfb/PAd791335Uk6bkFCCjBPJDnzZtnjZF5hlkFckBQ6QbSenHPLA1XIFDfvn27nFyy4egSrstTxgvp8lblc0PGbJYuWBfBMAKm2dCNkYNtTnFvJBgOv29IOGYoVFVYwYnWZ9GiRZmzADHc7iGtFQTzsRR3adXoGork2YKJTvkToKhRUSoUlpkTO+BMHpMK09HoNkt4v0JKqqdM/roIxnroHNSqgMKZLgyZjZMDDjjAGqSEw0gI5xpLXPgyPfvd735nifCLX/wic7IwMsjkGhbY4BYS1y+kAjcI6rdmobBZ3AYNGmTTUsTgDXkh7RCD/JMX3Mh/IyEcfgkj4V0MG4Uv6/OuUpfujJtQmeAqNaz7TK4J59fMAARYVZMtttjC7LHHHk0lG0OhBXQFskThgXsrDYlluD/5yU/axXqY9ZGn+HaAbgjDp444wV7c99M4v1V7FssCiJXFADAYwoUAdwGCnG6XgG6mhKFg0APJpcuAXyG0G46ubLMiv3zceeedmVWR9nXWWafHu1aZCEbm2FCCP6HZoD3qP7PMIHgBybtf4XhebM+J8s4i2If7euK2lnTTKRPsQ2xIbAXbcsMVVcnFEkxqYzH6pACQSWqkOCFDGCNdTGowDhdkwKHm48wzgKQLixuHEFCMl3NWgbRUCEceeWRWFTYcaQjlm/Sj3xdwzVKB+Xqy3N9yyy02bv5xK0rIH4M4brn6cfkYYBeURxKRskc/9sE9WIuArcSPXvEPsSgn7BR3bBC/SeMV/UnO3UqdCGA4L6okjIjjuoehCARUMhMnEIcjSnjmGysgAgTEd4X7OF2u39D1t771LbP22ms3taAn+abCCOVbegJ+AVK4RRVsKJ++G7/MEH8cAfwwje4xcGwII6blaqRbMKBswY8yJ03YX5ztgSX+XEL5aeN5yFZwJ15XcHNbP/dZM9fdCEaGxPCltUj7Ax+kJGwjIUOAGiWSDve5gOqDg1FTIFmELiFpYQnsZoSCxjggWkgwNp980kMI+W+VG39Bk/+LL744lyghlJQdeEC0OKIIwQjjVkBgQ5lG4QnepDtOeB6ylVA44vfLJ0530mexKZRMxBHBjQhQIFcUKOJXanQ/8/Kcc1SG04Dm6ou63n777e0SaFHPk7pDIL+2dMNK60vtzlQp2TUlKbaurryv9913X2us06ZNy1u1xYSWKcomhGAuuUgE/kNlLQmEDI3e7ULhCYdt+RJlb76/tPexBEMZhGnUzOMvKbnw2wg8/ERlOAo03NPK5ZdfbguR4flmBCMhvb6R+DohE3iSVs5lIBdpfOWVV8zHP/5x85GPfMSwUlWe0qgyleehOMEpCiOI0qjMee5X4qUjWKhr44ORhlwSlu4DmY2SogkGyXnv0n+m/lcCDzzwgDXYHXbYoamP7H55SgsV103EFnwiNaqERW9cpVYqgoVeFqWWcMHhO5E7jSgLuSgEdNN1cHW7YBVNMOmi5V1j+wZWpfvrr7/ekozfXNIKBu+WJeEpT0Z8aa1FmNXPsuPMjxTBFnjfkvKHXDJIIn5CZyp/ht/xLyI6uC8VwahFSBCAkGiuyYBbsyxcuLDLj2QIf1EHJIkSQKHrSVjAhWxcixRJMBaZIa6TTjpJotPz/yMg+52lxUbe1ylH7IcyBWPK0SXeeeedZ939QSUqavy7tueGCxUQz6XLjd1KfOKX+1J1EUmMe0hC3TPLN7MUmYjr379uBBA6qHEknFv7ENa9d+NzayxXh/hpdN5nn33MZpttZt54441GXjvy+Xe+8x1rrCwnl0YoFylLzqHyZyYJq2zxS5Avri34z+LuiUfidf3hFrKVULqi7M3Vl+X6/SYjS+gKhmEOHjUbq+WqRCPAry3gdMcdd0R70icNEegogq1YscK2XHvttVdDYDrdw7PPPmtXMaarxyKpKtkQ6CiCsbx1qF+eDbr6h/rTn/5k8dp9992DXbr6I9B8DjuGYPwuD7mOPvro5lHrIA2yBNzhhx/eQbnOL6sdQ7ChQ4fakUq6PirpEJCW/+yzz04XUH2bjiAYS17Tel1wwQVa5BkROPTQQy2GkyZNyqihM4N1BMEGDhxoWEpaJTsC77zzjtlpp53MGmusYXg3U0mGQO0JJr9kFDGRNRnE9fHF1rUbbLCB/SM69I2yPjnNLye1JhiTWNdaay0zZMiQ/BDrcE18F6O7/dWvftVuQNjhcDTMfq0Jdswxx1hjYK8ulfwQmDBhgsWV+Zwq8QjUlmD33nuvNYJTTz01HgF9mgkBNpWgJSviL+BMCSppoNoSjNka/OMUmvNW0rKoXLIOOuggS7Jm/6erXMZTJLiWBJOPo1dffXUKKNRrWgRee+01s91225kNN9zQ8D+ZSk8Eakew9957z2y66aaG3+BVikeAWegMJLHV0z//+c/iI6xYDLUjGO9cvBu4v9RUrEwql1w+gYC5jtb2LLpaEezRRx+1Bc3ooUprEWD1MUimO2p2x71WBPvGN75h1l9/ffPSSy91z6XetQSBUaNGWZI1s7Z/SxLawkhqQ7CbbrrJFi4zN1TahwAfoGnJbr311vYlokQx14ZgjGaxIpJKexGg99CvXz+z+eab2zXw25ua9sdeC4Kdf/75Wmu235a6UsBH/g984AN2p5o333yzy70TLypPsBdffNFuxXPIIYd0YvmVNs+y9skRRxxR2jS2ImGVJ9hRRx1lVlppJbNgwYJW4KVxpEDgnHPOsT2LM844I0WoenmtNMFkzYjTTz+9XqVSo9ywJRSDHlXeVriZ4qg0wb70pS+ZLbfc0jB7Q6WcCCxbtswwL3TNNdc0M2bMKGciC0xVZQnGuobUjJMnTy4QHlWdBwJPP/20XS5vm222MU899VQeKiujo5IEY4b8JptsYvbbb7/KAN3pCWUteipE9o9bunRpx8BRSYKNGTPGFtZ9993XMQVVh4xeddVVttzY9K9TpHIEmzdvni0k/Zu2miYqO/ace+651cxAylRXjmBf//rX7UZxrLehUk0Ehg0bZivJqVOnVjMDKVJdKYLx5yz9+PHjx6fIonotGwJvv/222XXXXU3v3r3N3Llzy5a8XNNTKYJ96lOfMp/73OdyBUCVtQeBRx55xGy00UZ2rUVm49RVKkMwmRWg2+nUxxSZcU+PJMuOmlVBoRIEe+aZZ8yqq65qN1qvCrCazmQIXHbZZZZk7rbEyUJWw1clCMbOHqussor5+9//Xg1UNZWpEIBcdX23Lj3B2DQb8LNMGGXfYDbTZt9fDn/rUO4Z0ZLnoflybEM6duzYbntVp7Ie9ZwIgYMPPthO2r755psT+a+Kp9ITDOPnB77ly5cnxpR9edkUm43d+e7CRu4c7nrqXLNhNzMLICL+xL9ERBhZWBOiybU813N+CPDZZfvttzdbbLGF4VtnXaTUBGNtB1qvKVOmpMJ75MiRpk+fPj02wHaVsKs9flyBQJBONs5Gjyv+vftMr5tH4MEHHzTrrruu/VGTNRfrIKUlGEbOMO7ee++dCmfCQUpapTihtQq1SG5Yn1D+fZx+fZYNAfnWOXz48GwKShaqtAT70Y9+ZInCzA3ew5IKXTlIIsK9tEjixhk/PPNlt912s91F3HlHo6WbOXOmvof5QBV4f95559nyodtedXnfEkuUE7oKEODYY4+1S7BdfPHFhu4iMwAaibxL0YKhg5aKM+9yQjSIE0cwSCVCGIjovr/Js046gwEVjX/4GIAXayQyMMRZMHf94YaeOJGdcfgtqcpSSoIx8vfRj360W+GwLBvkaWTo+OE9CpJI4XLedtttLckoLIwljmC0YirdEQAvMAQb93B9UXGBPe+2+OHct2/frnLALwNHlBFnyiiuPJlO9aEPfcjceeedbjSVui4dwWSxlMsvv7wHkKxWxHsQK/hGibRg/nMKFCNBIFwcwdCh0h2BKLxcX5AKEvoVm9sjcN9j8efeu7po4b73ve+Zrbbayup84okn3MeVuS4dwfr3728+//nPRwI4f/58C/xjjz0W9EPXkFrTF2m1qGURDAbS+UKtqwTrjopg1921+51UWj6mUrEJ6Xxs/Xu0Eh97DLDG4qxZs+yqYfvvv79ZsmRJ90grcFcqgvExGcNvNKjBdxL+B3v22Wd7QCzvV37XQwpaAlDbujUr7oRJUlOLjk45JyGY+BEiCTZCPJ4jEEoqOSpDn5D8RMsPtS+//LKoMNdcc40tF1q0qklpCMY0KBarTDo8O2fOHPsiHarVIA8fmqWwOXPvEkoIJ4VNwdG98b+NVa1Ai0ivkEdmxXD2BzBkUCkUv99b4PMIRBPSSRjW6zj66KMNa3j4cuaZZ1qSMem7SlIagmH8TOhlYm9SgSQTJ07s4R1CQRZeuBk9pIAhnRBOAtD/5xldSs6QyyWc+Ov0My07hJAD3BiddSsxnoFhSHDneZywMhgjj/fff3+kN+akoqtKCx2FEYnMYjEP/vCHP1jgzj777NQRXHDBBZFDvpCFWjKONBgPfvzaNHVCOiwAlZU7tSxNCxaCim7gddddF3rU5fbuu++aPffc044wV2X/t1IQbOeddzYMbmSR5557zrCISl2m1mTBoF1hmMdJzwChggq1YBAR97gKjIGrpIvHMprIWphs9BF6B28XFlHxtp1gl156qS2A66+/PiqNDd2Zgc2+zCqtRcAdKBIi+YMW8q7rDzq5KeX9Kq6X4frlmp9uWS6dWT5ll7YSjBnUbKDNS3Mzwkx7Rp4WLlzYjBoNG4FAiBwQgpaJrqEIhPPLEjdp5cSfe2b585///OeuU6LrK664wsZ/3HHHJfLfLk9tJZgMMqSpvaKAYmHLK6+8MuqxujeBAARhQINPIwxEQCLI5Y7Kop5ylMEP/BGG+7jyZfDjySefzJS6k046yaaDqXRllbYRjFkZFNLo0aNzwWbFihVWl/v9JBfFqsSOvsrQOqSCFFHvVDLiKP5CrZ9A+sADD5hmdyQdOnSoWXnllXt8T5M42n1uG8FY9nrjjTdONIE3KUj09/13gKRh1V/rEYBcDz30UFMR8+63yy672B81m9XVVEIiAreFYAxI0HpNmDAhIlnZnF944QVDt0Gl/AgsWrTI8EtSHsLMno997GP2m2fZFqRtOcFY+J8JnHEvvs2Azrc0XRynGQRbE5Z35kmTJuUWGX9bUGkfeuihuenMQ1HLCcYkToAoaq+oadOmmenTp+eBjeooEAFWZ3744YdzjYHBDmzr5JNPzlVvM8paSjBmwPP9gikvRQm/soSWAigqPtWbDQFGJNmGKm/hJ11IxjB+GaQpgjFS5H/3iMvUkCFDzGqrrWaef/75OG9NPfvPf/5jh5ObUqKBC0WAd+Vx48YVFseBBx5o1l57bXP77benioPPCbKEn5ypCOJGQhtFkJlgMjWG2iKJMNsCv62YDU0XoWwvu0kw6hQ/DM8X+c2S/8gGDhxop9/F/Zzr403PBxvlM4Qcob+y/XBx98nYEdDAbHXmopGgJAxnzTs2b2iF0BeP+iGzFfFrHPEI3HbbbYZBiSKFXVs22GADs++++yb+FOTOrZS0SUMS9d1P/EWdMxGM6TF8oZf5Z1GRY+g0tSwcChFvuOGGqHTk6n711VfXflucXAFrsTJ+N2GKVNHCeprY3Y477mj/kuevaJaFi5LQ3+x0G9ERZeNRusQ9E8HchBC5Ox9NFMtoIc/l4JeEVggThxkGViknAnQPW/VRmOUnxP7kfOONN/YARhoLd6ICbiytjr1nldQEo28qrReR0lXEzRcWDZUMyXnzzTe3c9mYp1bkwXY4hxxySKFxFJn+uuumJTnqqKNaUj78xCv2J+dBgwb55tr1uw3zJ2WAA2IxkAfRskoqghERfwm7w+B8MCYRvqy++uo9MsbIjiRez//bkEJxKA4Hln0TUrnnPfbYwzdX20hIz4wGQ/7aZhSxGUlFMCJ2EyrXoVkZsg+v+OH8k5/8pJm0alhFIDUCgwcP7mGzoQnG2DCDHK4weIfdhl6BXH9x14kJJpFBMl745KD1Ci2T9s477xhmOpPAtdZay4waNSouHfpMESgEgVdffdX+mIkd0vs64YQTgvHw2hN61YlyDyoJOCYmGEQKvezBbhIfJcuWLYt6pO6KQMsQYA5slEjj4Y8UinvhLZgMVYYiIlEQjMSoKAJVRECWNZC0Y8vMaaVnxiBe4YMc9E9D71kkSFjus18Sq2dFoOwIyJ/1NBRySNewGXKR7+i+XdlRKVn6KAi2oJUh9rjf5P2k41fCaU/AR6fa90qwHMpP5rDRnZDWnpqQkdRGwsgVtaUbLtQVb6RHn5cTASVYDuVCC+R3keXd1Hd3o2PUCnK5rZYMGrlubhi9rhYCSrACy4tWLDT0K1HSatH/9yVqdozvz+1a0j2V9wVIzcG9bIbnPnfDxVUAfnx6nx4BJVh6zBKFwIghGOcoiSISpIwaVBJdfDZBv3Qt+YQicRGeGSJM++E5fmkpuaeFxK/MHG9UCUh8es6GgBIsG27BULQGbBzHgAUfNUOtkxtQjN9141pI47vLvXQjhVDiLmcIBnHciaukDTfIJS0d/kkjaVUpBgElWI64YsBy8Kd3FAEkSvn+IlsB8d7FwIgMeog//xxFTPEHwUKTAkgbz1wR4rluep0fAkqw/LDs0kQLEWpFujw4F4xAQgZpXQhHqwKJoiREFNcvOkLhQ+GUYC5y+V8rwfLHtEujvOd0OSS8iHo3k+AhosgzzkowF432XivBCsSfwYVQSxIXJd1ECBTXvYSAce93SrA4hFv7TAmWA96hb1Z0Exk8wNhF+F196tSpctvjTBgZ+evx0HFAJ7rdwQrnsbZgLhhtvlaC5VAAtDgMi8t0J37SgwC0NC4J1ltvPbtRAdulikAWwhEm6eRSdKKbOBgUITzx8z6FaAsm6Lb/rATLoQzozmHUvHNxcO0OkUsURx55pBkxYoTc2rN0I6PCdPPs3TBAQlcRHVwLmSFaaLoVcQgJRRWtL+4qxSCgBCsGV9WqCFgElGBqCIpAgQgowQoEV1UrAkowtQFFoEAElGAFgquqFQElmNqAIlAgAkqwAsFV1YqAEkxtQBEoEAElWIHgqmpF4P8A7XBfeASI2aEAAAAASUVORK5CYII=[/img][br]If Han asks for 2 sides and the area, do you think this will be enough information for Han to draw a congruent triangle?[br]
If Han asks for 2 angles and the area, do you think this will be enough information for Han to draw a congruent triangle?[br]
Jada and Tyler were playing the Info Gap, using Card 3.
[size=150][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAYgAAAC0CAYAAACOjLtEAAAgAElEQVR4Ae2dCfhN1frHQykqQ0lkKFEqZUjmEkW30i9EiJsh97rlynQzRIaIMpTSIJkjhaJSugmZmyikEEkhY7rmhqv3/3zf/12n7Tjj7+y9z95nf9fznOecs4c1fNY567vXu9Z612nCQAIkQAIkQAIRCJwW4RgPkQAJkAAJkIBQIPgjIAESIAESiEiAAhERCw+SAAmQAAlQIPgbIAESIAESiEiAAhERCw+SAAmQAAlQIPgbIAESIAESiEiAAhERCw+SAAmQAAlQIPgbIAESIAESiEiAAhERCw+SAAmQAAlQIPgbIAESIAESiEiAAhERCw+SAAmQAAlQIPgbIAESIAESiEiAAhERCw+SAAmQAAlQIPgbIAESIAESiEiAAhERCw+SAAmQAAlQIMJ+A999953gxUACJEACQSeQ8QKBxr5ixYpy4403Rq1rXNOoUSM57bTTQq8PP/wwdP0XX3whAwYM0NecOXNCx/mBBEiABDKZQEYLBBrzAgUKSIUKFaIKBMQB10BArKLw888/h+q9TZs2oc+TJk066brQCX4gARIggQwjkLECgYYfPQI06Hj6j9aDaNiwYdRzqGuIhlU4cAzxMZAACZBAphNwTSDuvvtuWbBggas8IRII0QTCiEgssxF6ElZBgFhAdBhIgARIINMJuCIQAwcOlLx58+oTfdWqVWXo0KGyYcMG19hGEwgIA3oZCPiMfE6ePPmUQWqc69KliwqFVSxcKwATIgESIIE0EHBFIFCu6dOnS6VKlbRBrlatmr43btxYpkyZIocOHXK06NEEAsfz588vGGPAOAW+4x1jErF6FY5mlpGTAAmQgEcIuCYQKO/q1aulRYsWIZHo3LmzXHTRRVKsWDHp1KmTYyaoWAKBHsSoUaNOqg70Fi655JKTjvELCZAACQSNgKsCAbhHjhzRJ/U8efLI6aefLi+//LK88soroWmmMEE9/vjjtpqg4glEeKVjnAHCYcYwws/zOwmQAAkEgYDrAmGgwuSE9QloiNGTQNi8ebOKQ+XKlSVHjhwCExQEJFUTVDSBMEJg8mTese4B+cI7AwmQAAkElUDaBALAV61aJc2bN9fGuFatWrJp06ZQPSxatEg6duwohQsXluLFi6sJauHChaHzyXyIJhCYoYQxiPBprJilBIFgIAESIIEgE8h2K4hGFbN+6tSpoy98zo5J5vDhw9K/f38588wz9QVzkzUcPXpUB7KzsrK00cYAN0xQGzdutF4W83M0gcBNOIdB6TfffFPzj3d8x3EGEiABEggygaQFAk/dEAU8YWORGRpSvDD7J5X1ARAGxIF4u3fvHrFOIAqDBw/W62CCuuuuu9QEBRGJFZC/aAvlcB/OoyeBtC+++GKKQyyYPEcCJBAYAkkLBBpxNKZO2OdhcmrWrJk21LVr15Zvv/02akXMnz9fOnToIOedd56aoB588EHJrgkqaiI8QQIkQAIBJpCUQGA6KJ6ynRAHUwcYkO7Xr5/kzp1bzj77bJkxY4Y5FfH94MGDMmHCBLnttts0bzBBPfHEE0mZoCJGzIMkQAIkEHACSQkEzC9Wx3VOsps2bZqUL19eG/0ePXoklNT69et1XOTqq6+WnDlzqglq6tSp8ssvvyR0Py8iARIgARL4k0DCAmGmhIbP+PkzKvs/ffbZZwIfTui13HTTTbJt27aEE3nvvfekffv2ki9fPilRooTABIWZUQwkQAIkQAKJEUhYIDCQi4ba7QCT0yOPPKKL6tDYv/HGG0ll4aeffpKxY8dK/fr1Nf/Vq1dXE5R1Sm1SEfJiEiABEggIgYRb/HQJhKkHmIquueYabeQffvhhczip93feeUdnM11xxRVqgmrSpIkg3t9//z2peHgxCZAACQSBgG8EApXx6aefStOmTVUk0CPYsWNHUnWEVdmY/YQwd+5cHU/BQDhMUFjNTRNUUjh5MQmQQIYTSFggzOpiN8cgIrHHrKW+fftKrly5dIorFrYlEvbv36/jEMeOHTvp8r1798oLL7ygYxwwocEENWzYsJNWdZ90A7+QAAmQQEAIJCwQWCCHWUzwnxS+Yjr8uxvs0BvAbCU06hijiBdmzpwps2fPjnkZ1mH07t1bypQpowIEExRmU504cSLmfTxJAiRAAplIIGGBQOGx/sGsOIZQmBXVGJ9IR/jkk08EjThEAusgdu3aFTEbu3fv1t5DMk7/sB9Eq1at1P1HyZIl1QSV7t5TxMLxIAmQAAk4RCApgUAe0JNA4wlRwCvdjeZ//vMf6dOnj3p/veCCCwQD0eFh4sSJMm/evPDDCX3/8ccfZfTo0YKV3RCiGjVqqAkKnmcZSIAESCCTCSQtEF6FgZ3pypUrp404HAeagF7PoEGDzNeU3tFjwaI9bCaEMRAMmMMExUACJEACmUggYwQClfPxxx/r6mk86d9xxx2yc+dOdduxbt062+tu1qxZ6qocQgETFHahS3dvyvZCMkISIIFAE8gogUBNwgSGdRIQCbjthvnJybB9+3Z56qmnpGbNmiET1PDhw2Xr1q1OJsu4SYAESMBxAhknEIbY5MmT5aqrrtJGGy7C3QgrVqyQbt266boKbKcKE1T4/hZu5INpkAAJkIAdBDJWIADno48+0m1L0Zto1KiR9i7sgBYvjj/++ENee+210KI+TA+GCWrx4sXxbuV5EiABEvAMgYwWCFA+cOCArm2ASGDr0g8++MBV+FgjApNT1apVtTcDUxS+J+N40NUMMzESIAES+B+BjBcIU9NYCQ4fTBAKbFmajrBkyRJdj1G0aFF1PghPtTRBpaMmmCYJkEAiBAIjEICxcuVKNTVBJLDALpmFc4nATPQaOAfE9FiYvZAXmKC6du1KE1SiAHkdCZCAKwQCJRAgCvffvXr10oYZ6xnS7aBvy5Yt2qOpXLlyyAQ1YsQIwewoBhIgARJIJ4HACYSBjdXVZcuW1UYZYwJeCBCrBx54QLAi/IwzztDNkqZPn+6FrDEPJEACASQQWIFAXWNaasOGDVUkmjdvLuGeXtP1ezh+/Lhgmi4W+8EEhZ4OTFAYw2AgARIgAbcIBFogABluwHv27KkNcenSpWXp0qVusU8onY0bNwrWcVSoUEHzWKtWLYEJCj6iGEiABEjASQKBFwgDd8KECXLZZZdpI4yV0V4M2OyoQ4cOug8GTFDNmjUTmqC8WFPMEwlkBgEKhKUely9fLnfeeaeKRMuWLeW3336znPXOxyNHjggE7dZbb9W8wgSFFdzIPwMJkAAJ2EWAAhFGct++feqxFbZ/DGJjnMLL4auvvlK368aTLUxQI0eOlD179ng528wbCZCADwhQIKJU0vjx43VnOQjFM888E+Uqbx3Gnhf33Xef5MuXT3Lnzq0mqFdffdVbmWRuSIAEfEOAAhGjqpYtWyZZWVlqxmndurXAx5IfAjZRGjt2rNSvX1/zXqpUKTVBYaEgAwmQAAkkSoACEYfU3r175aGHHtKGFt5hsWmQn8LatWt1z26z5uP6669XExRmbzGQAAmQQCwCFIhYdCznxo0bJ5deeqkKxfPPP28545+Pb7/9tqAnlDdvXjVBYe0HTVD+qT/mlATcJkCBSII41kiYxWvt2rVL4k5vXQp3IxC5unXrhkxQ3bt3913vyFtUmRsSyDwCFIgk6xSzg/71r39pw1q+fHlZvXp1kjF463Lkv3fv3qEBeZignnzySdf2zvAWDeaGBEjASoACYaWRxOeXXnpJMPiLWU4vvvhiEnd699I5c+ZIq1at1Px05pln6p7b2PiIgQRIIJgEKBAp1Dt8IzVo0EBF4u9//3sKMXnrVvSSMLX3hhtu0LJh7AUmqFWrVnkro8wNCZCAowQoECni3b17tzae6ElUqlRJ1qxZk2KM3rr9008/1VlcWK2NMkI0YIJK114a3qLD3JBAZhOgQNhUv1h3gI1/0IhikV0mhlmzZqnZKVeuXAITVIsWLWTGjBmZWFSWiQRIQEQoEDb+DBYvXiy33XabisT9999vY8zeimrnzp0Ch4bYXxuCCBMUBu6/+OILb2XUhtygTHXq1NFyoqwFChSQgQMHxo35xhtvDN2D+8zrww8/jHsvLyABrxCgQNhcE7t27dJVy2gQqlSpIuvXr7c5BW9Fh9XZ2KuiePHi2gjCBAXxgEPBTAjoFbZp0yY0qwsNfP78+WXUqFExiwf37F26dBFcb339/PPPMe/jSRLwEgEKhEO1gZlNJUuWlBw5csikSZMcSsVb0WLRHfb6hjieddZZaoJ6/fXXvZXJJHKDhh1l+e677066C4KBHkKsgPtwPwMJ+JkABcLB2kMDYVxyd+rUycGUvBX1Dz/8INjGtWrVqtrAYiMmmKDWrVvnrYzGyQ2EAQ09pv9aA3oHEIlYgQIRiw7P+YUABcLhmsLObzDBoMGoXr26YIe4IAU4PHzwwQelaNGiyqB27dpqgsK2qn4IEAKMO0DsYR5CXcLEFN6rCC8L6hs9R4xL4UXTUjghfvcDAQqES7U0ZswYtdOffvrpMnXqVJdS9U4yJ06ckGnTpoX2AIcJ6p577jnl6dw7Of4zJxAJNPh4ofcQr7HHwDZEBNdbB6vbtm37Z6T8RAI+IECBcLGSFi1aJLfccos2HBjADGrYunWrDB06VK699lplARMUPOZi8yOvBfQC0IMYMGCAvtDwY1ZTPJEILwd6ILg3yPUezoTfvU+AAuFyHWGKqDE5we/R5s2bXc6Bt5JDw/nAAw/IBRdcoGIBExRmCHlhu1fkDb0AvJsAYUAvAiKRbIA4YMEhAwn4hQAFIk019cILL8hFF12ks33ocltUECZPnhzylmtMUHBRnq6ABj3SbCUjHMn2ItALQS+CgQT8QoACkcaaWrhwYWjXN8zyYfh/AuhVDRo0SOAtF0/wZcqUURPUhg0bXEWEBr1ixYqnpIlZTciXNSSy22DDhg0jCo41Hn4mAS8ROPlX7qWcBSQvO3bsULu0GdCMNzsmIFhCxVywYIHAEWLBggW1UcYTPUxQGPR2OmCwGfWCldOmt4DeA0QDjb0J2BskT5488v333+shjFugN2RWluMdcSAuc8zcy3cS8DIBCoRHagcmJ0wFPeecc2TmzJkeyZV3snHs2DGZMGFCaF0JGuSWLVvKu+++62gm0VswPrbQwOMF05MRDCRuNpH6+uuvNS8QkfB7IGzWsQxHM83IScAmAhQIm0DaEQ2elm+++WZthHr27GlHlBkZB0xNMP+UK1dOWcEE1aNHD/nmm2/SVt5NmzalLW0mTAJOEaBAOEU2m/Fu375dF5bhSRVige8M0Qn8+9//Fph4zj33XBULPKmPHj06+g08QwIkkDABCkTCqNy9EHtGX3jhhTrrZfbs2e4m7sPUDh8+LHC5Xq9ePRUKY4KCgDCQAAlkjwAFInvcXLkLJqe6detqg9enTx9X0syEROBBt2/fvlK2bNmTTFDffvttJhSPZSAB1whQIFxDnb2E4PgOjv5gcsIqbLgTZ0icAAaxW7duLXnz5lWGWOCG3hkDCZBAfAIUiPiMPHHFc889J4ULF5bzzz9f0rl4zBMwspEJzDrCTDGz+Q8Eo1WrVvLBBx9kIzbeQgLBIECB8FE9ozEzDVy/fv18lHNvZRX7hvfq1UvgAwo9s8suu0wwa2zbtm3eyihzQwJpJkCBSHMFJJs8TE4dO3bUhu3222+XvXv3JhsFr7cQeOutt3Q9Re7cuUMmKGz2xEACJMA9qX37G3j22WelUKFCanaaN2+eb8vhlYzv379fp8diy1T0KowJCu5QGEggqATYg/Bxzc+fP1/g/RQN2qOPPurjkngr66tXr1bfT2Y1tDFBcU2Kt+qJuXGeAAXCecaOpgD/P3CXDZHIysqSAwcOOJpe0CLHGpRmzZpJzpw5QyaocePGBQ0DyxtQAhSIDKl4rB7GDCe4EH///fczpFTeKcbu3bt1q9QaNWqoUJx99tny17/+VbcT9U4umRMSsJcABcJenmmNDcJgbOhDhgxJa14yOfFPPvlEN30qXry4isXll18uvXv3Fuw/zkACmUSAApHG2oRZKNIrlSxhquY//vEPjbdx48Zy6NChVKLjvXEIwPNukyZNQvWIle8TJ06McxdPk4A/CFAg0lhPEAfsbQA30NaXHVl65plndA+FEiVKCGfi2EE0dhzY12PEiBFSpUoVFQtjglq2bFnsG3mWBDxMgAKRxsqBQDi5RwAc1dWqVUsbrCeeeCKNJQ1W0itWrFD3KEWKFFH2MEHBN9SePXuCBYKl9T0BCkSaqhDCAIFwOmCHOuzIhrSaNm0qR48edTpJxm8hMH36dN19DvzxgglqypQpliv4kQS8S8D5Fsq7ZU9rzoxAvPnmm7odJd6d3I7y6aeflgIFCkipUqVkyZIlaS17EBPHdOTHH39crr32WhUK7ByIWVArV64MIg6W2ScEKBBpqiiIARZiYYMbvCpUqKANR9euXR3L0XvvvSc1a9bUdEaOHOlYOow4NoGlS5fK/fffryvh0auAW/L+/fvLvn37Yt/IsyTgMgEKhMvAYyVnehUYuHYqbN26Vf72t7+pSLRo0UJ+/fVXp5JivHEI/Pe//5WpU6dKgwYNtD4gFjfddJMei3MrT5OAKwQoEK5gTjyRhg0bao8i8Tuyd+VTTz0l+fLlE+znvHz58uxFwrtsI4DNjB577DEpX768igVMUPfee69gzQUDCaSLAAUiXeSjpNulSxdXBALJw8lf9erVtUHCGAWDNwgsWrRIJxYULFhQ6wYmKPjaohsVb9RPkHJBgfBYbWNcAiLhVsCT63333acNETbQOXHihFtJM504BGD+mzRpkvzlL3/R+jEmKMyMYiABNwhQINygHCEN/PHx1L548WJ9YRYTNgPKnz+/YPcztwMGrc8991y54oor5OOPP3Y7eaYXh8A333yjs92uuuoqFQvUFbZSXbVqVZw7eZoEsk+AApF9dindiQFpzF6CIODJELOY2rRpkxZxMAXB/s3VqlXT/GC/CQZvEsDOgu3atVNBx28Hoo7xi4MHD3ozw8yVbwlQIHxbdc5kfMuWLdr4oOGBYDF4lwAWPY4fP17q1asXMkHdfPPNMmPGDO9mmjnzFQEKhK+qy73Mwq8Q/AmVK1eOZgz3sGc7pa+//lqwTzncekDcYYJCL+Pzzz/Pdpy8kQQoEPwNRCXwzjvvhJzPjRkzJup1POEtAlgQifGJPHnyqFjABDV06FA5cuSItzLK3HieAAXC81WU3gxu3rxZTU14Km3fvn16M8PUkyIAV+8vvviiTn5A/eEFE9Trr7+eVDy8OLgEKBDBrfukSj5s2DDJmzevDqavWbMmqXt5cfoJfPnll/Lwww9L6dKlVSiwSBIr6teuXZv+zDEHniVAgfBs1XgvY3PnzpXrrrtOGxjuy+y9+kk0RzAdtmzZUs444wytyyuvvFLwAHD8+PFEo+B1ASFAgQhIRdtVTMzHh30b5ooOHTrYFS3jSQMBrMx+/vnn5frrr9f6RJ1iRtScOXPSkBsm6UUCFAgv1ooP8oQNiM466yx1Xw3zBYO/CcC7cM+ePdXDMIQCJihsXbt+/Xp/F4y5T4kABSIlfMG++e233w7tb4CV4QyZQQCr+ps3by45c+YMmaCw0v63337LjAKyFAkToEAkjIoXRiKwadMm3fgGT50dO3aMdAmP+ZQA9qfA3uY1atQ4yQSFBwOGYBCgQASjnh0vJebZ586dW6pWrSobNmxwPD23EsCWrU7u9OdWOVJNBz6funfvLsWKFVOxgIsYPBBkUl2nyigT76dAZGKtpqlMME1UqlRJTRMvv/xymnIhOsiK7VUHDBgQNw9o/NH7gV8sE+AsceDAgbpFK86ZV9u2bU/ylQXxgOddvBJJy8Tv9/c33nhDmjRpEuICB4LY5AobIDFkFgEKRGbVZ9pLs3HjRoHbcDSqnTt3dj0/aKzxdAu36fEabQjBJZdcouJgFQg0/Phunc0D54qI1+qKHZ+N510ITbz0XIfhcIK7du0SbDxVpUqVkFjANTmm0TJkBgEKRGbUo+dKMWTIEJ1nD/s1VmO7EdBAwysuGms08PEabDTwuA5OCa0CES2viA+CYkJ4/OHfzXVBeIeLeDwQFClSRMUCYtqpUyfBtGgG/xKgQPi37jyfczyBo8HGgiw3NrnB07x5oo8nEMgbGjFcj2sTEYhwIbH2JtDrCLJAWH+M8CaLrXONaQ4mqNGjR1sv4WefEKBA+KSi/JpNDGLec8892lh069bNtWLEEgiIAsYojAkpEYGAjR0NnrkHBUFPBaIBYbCam1wrpMcT2rFjhwwfPlzHpYxY3H777QJnggz+IECB8Ec9+TqXf/zxhwwePFhy5colN9xwg2zdutXx8sQSCDzdWve6iCYQaPQrVqyowgDTEsYhGLJHYMWKFfLPf/5TChUqpDwh0OCLLW8ZvEuAAuHdusm4nGH2yzXXXKNuqGfOnOlo+aIJBHoCGMA2pihkIppAoIcAUcA9EBQ8BXNBYOrV9sorr8gdd9yhPMEUe47A5QeD9whQILxXJxmdI2xs06JFC20cevTo4VhZIwkExgnw5BreE4gmEOGZM2YmxMOQOoFt27bpPhV4aDAmqKysLJk/f37qkTMGWwhQIGzByEiSIXDixAkZNGiQrpeoU6eO/PDDD8ncntC1kQQCYwWmIYr2HmugGcKC+8IFJqEM8aKYBJYsWaK+nyDgYIx3LMyDiDCkjwAFIn3sA58yNq65+uqr5ZxzzpHZs2fbyiOSQODJH417+AszrfDC8Vi9A5iX0HhZzVO2ZpqRye+//y5YZHnrrbeGxBwmKGx8xOA+AQqE+8yZooXAV199Jc2aNdPGABva2BUiCUS0uMNNTBCCrl27yuLFi1U08P7000/rU611amu0+HjcHgJbtmzRyQ2YJmt6fJhgsHDhQnsSYCxxCVAg4iLiBU4TgIsGuLZAI4D9CH788ceUk0RDnuiAMq61NvzoSUA0TKOEd3xPNL6UM88ITiEAUcAOeOhtoj4KFiwoGMNywjx5SuIBPkCBCHDle63omNmEp0XYn9966y2vZY/58QCBX375RSZOnCj169cPCTgGuV966SUP5C7zskCByLw69XWJsEFN06ZN9c/fr18/X5eFmXeWAFzNY1LB5ZdfHhKLu+66S02DzqYcnNgpEMGpa9+UFAOVZsYRBiv37t3rm7wzo+khgKmx8LabJ0+ekAmqd+/esnPnzvRkKENSpUBkSEVmYjHg0+fKK6+U888/X959991MLCLLZDOBI0eOyLhx46Ru3bqhXgVWw0+YMMHmlIIRHQUiGPXs21Jiv2uz9wAGslMNcPuBgc3PP/9cMPceg5/Lli2TtWvXyp49e1KNnvd7iABmyD3yyCNy6aWXhsTi7rvv1vr2UDY9nRUKhKerh5kDAeyFjPEIzF6Bi4affvopKTAY2IQYPPvss+qC+rHHHpOxY8eqh9lZs2YJXD/A1QMakz59+uhxTLFkcJcA1qBgSjEeBPAeK2AtCq6JtiYl/Pi8efPk3nvvVc/C+B2dd9550rdvX9m9e3esZAJ/jgIR+J+AfwC8+uqrUrZsWbnwwgvl/fffj5txrNjG/smYwgoTA3wrQSxiBfQiEDfGQJ577jk6k4sFy6ZzaMzNNGcsWMSUYvjLgoPESAsXUY/GiSKmJIcH1B1eqHe8W8PBgwdlzJgxUrt27VCvonLlyjJ58mTrZfz8PwIUCP4UfEUApqDGjRvrnxs9gWgBs6H69+8vU6dOzfYg99KlS3WuPbZSZXCWABpyNPwmQDQgFlgYZw1Yi4Jp0Gj80RMIFwjEYXXJjuut8VrjWrdunWAgG2KEuPCCn7CVK1daLwv0ZwpEoKvfn4X/9ddf1RyEPzQaEDwVWsOiRYu0YV+zZo31cLY+Hz58WMaPH68mqHi9j2wlwJuiEoBoQAyswSxYhDBEEggIglU08Nn63RqX9fPcuXNVkHLkyKHxwgQFs+a+ffuslwXuMwUicFWeOQXGLnWYA1+sWDFZsGCBFgzTHeEI0G7bMnxFjRw5Uo4fP545AD1eEggEehGRQjSBgEnKuioebtrDxyMixYfV+xiTwPgWTIs1a9YM9Sqw5zZ6okEMFIgg1noGlRm9hEaNGumfGRvS4Klv//79jpQQIoGBbgZ3CMD0Ez6GYFKOJhA4D5OSGX+INIZh4rC+48Hitddesx7SmW5w54EHEGOCatWqlWD/7aAECkRQajqDywmTE2Yf4U+MhXVHjx51rLQY7MbGRwzOEsCTf/jGTtYUYwmE9bpEP2PPbIxvRQsY1zBOJfE7w9ocDKwfOHAg2i0ZcZwCkRHVyEKAwLRp06RMmTJSsmTJuNMks0vs2LFjKkYbN27MbhS8Lw4BjCPkz58/6uAybrdbIDp37iyo23gBq/rh2bdatWqhXkX16tV1anS8e/14ngLhx1pjnqMSwAK4O++8U/+8I0aMiHpdKic++ugj3YY0lTh4b2QCiYgD7rRTIL7//nuJNSMuck5FPvvsM+nWrZsUKVIkJBatW7fW49Hu8dtxCoTfaoz5jUsAs40wfRGmgObNm8dd+xA3wggXDBkyRDZs2BDhDA9ll0Ci4oD47RSIFStWpLwOAptfwVGgGasoXLiw7mURPsMuu2zSdR8FIl3kma7jBDDzpHTp0upqYfny5bamh6m0U6ZMsTXOIEeWjDiAk50CgckHiSy8TKR+MBvqySefFCy+M2JRq1YtgV8xPwYKhB9rjXlOmMDq1aslKytL/6yjRo1K+L54F2Jw8qGHHop3Gc8nQACzjtCYYuU09igPf0E8woOdAoG9JPA7sTvAFImxjUKFCoXEol27djo7yu60nIqPAuEUWcbrGQJYu9CrVy/9k7Zs2VKwg50dYfDgwdzRzAaQmIqK6azRXhCD8GDuSXQaa/j91u/Dhw933KUKptBiUafpVRQtWlSGDh0qWIjp5UCB8HLtMBfbIGEAAAQwSURBVG+2EoBJqFSpUrq4zo657HiyxVMig78JwCWLW558t2/fLsOGDdMFgEYs4BcKTiO9GCgQXqwV5skxAph50qBBA32SS3XRGxwBcp8Kx6rKtYh79uwphw4dci09kxDGxTp27KjuRIxYtG/fPuZ6DHOvW+8UCLdIMx3PEMBCOqyQxZ8y3N6dzHd4FC1XrlxKcSSTHq89dXzCDiYlSpRQ7652xJVqHEYo6tWr54n/CwXCE9XATKSDAExEqf6heb8zjXbQuXbt2jUdf4lT0qRAnIKEB0iABEiABECAAsHfAQmQAAmQQEQCFIiIWHiQBEiABEiAAsHfAAmQAAmQQEQCFIiIWHiQBEiABEiAAsHfQEYSwKpV685iGVlIDxYK+yZgnwQGdwhgC1Yz4wszn+CKPJEd9BLNHQUiUVK8zjcEMH0V88nx52Fwj4DxqQT2DM4TMP6ojIsSPBBhHw3s422XSLAmna9HpuAiAfwx4PQNO5KFb3jvYjYCmRT2jwZ3CoQ71Q9hgCBYA3xTgb9djikpEFa6/Ox7AvjTYKtK83Tl+wL5pAB4ekWPjdzdqzCYUSP1kiEQ+B/YESgQdlBkHJ4ggN4Deg0wMRlzB94ZnCUAUcCTLJ5eKRDOsrbGjgehcCEw5lU7vNwiLQqElTg/+5oAnmLxpzEBT1JosBicI2BMemiYECgQzrG2xgzu+H23bdtWJwVggBq+wWDms/M3T4GwUudn3xIwtlfMojHBTlusiZPvJxOAmQMvEygQhoSz7/idG1MSehGoAzwc2e3DiQLhbD0ydpcImMFRM+UP7zA3hXfBXcpOIJJBIwXTEp5mTaBAGBLOvuN3be0tIzXUA+rDzt88BcLZemTsLhAwjRJMTPhzmBf+QNanWxeyEqgk0Bg1atRITRxY+4AXTB54ssVnY3YKFBSXCovB6Ui/bRyPNHCd3WxRILJLjvd5hkC0PwWEws4/i2cK7JGMGO7Wd9jAIRA4BsFmcIYAxDnSVFY8FNnJnQLhTP0xVpcImN4D3sMDBIJrIcKpOPvd1IezqQQ7djPeZv3N4xh6cxAOO2fuUSCC/VvzfeljmZHYWLlfvWTuPHMzlRU9NesLvTaraNiREwqEHRQZR1oIYFAOfwjrIKk1I+a89Rg/O0sAT7LouTE4RwCM8bu3vpxKjQLhFFnGSwIkQAI+J0CB8HkFMvskQAIk4BQBCoRTZBkvCZAACficAAXC5xXI7JMACZCAUwQoEE6RZbwkQAIk4HMCFAifVyCzTwIkQAJOEaBAOEWW8ZIACZCAzwlQIHxegcw+CZAACThFgALhFFnGSwIkQAI+J0CB8HkFMvskQAIk4BQBCoRTZBkvCZAACficAAXC5xXI7JMACZCAUwQoEE6RZbwkQAIk4HMCFAifVyCzTwIkQAJOEaBAOEWW8ZIACZCAzwn8H3ajHyc+zSF1AAAAAElFTkSuQmCC[/img][br]Tyler asked, “Can I have 2 sides and an angle?”[br][br]Jada told Tyler that one angle was [math]16^{\circ}[/math], one side was 5 cm, and one side was 4 cm. Here is the triangle Tyler made:[/size][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAASkAAABJCAYAAABhGtBsAAALHklEQVR4Ae2dBagUXxTGnx0oit0+UVSsZ2J3t9jdKAY2FnajYGCL3f1Exe5WbLEbFQO7UfH8+S7/u6z7dnfc59s3szPfhWF2d2Z37v2dO9+Nc+5smDCRAAmQgIUJhFk4b8waCZAACQhFipWABEjA0gQoUpY2DzNHAiRAkWIdIAESsDQBipSlzcPMkQAJUKRYB0iABCxNgCJlafMwcyRAAhQp1gESIAFLE6BIWdo8zFygBC5duiTYmOxDgCJlH1s6viQQp7CwMKlYsaLjWdgJAEXKTtZ0cFnevXsn4eHhEhERQZGyWT2gSNnMoE4tTt++fZU4jR49miJls0pAkbKZQZ1YnMjISEmRIoWgN0WRsl8NoEjZz6aOKhGEKWXKlAKhQqJI2c/8FCn72dRRJWrYsKF06NDBVWaKlAuFbV5QpGxjSucVZMaMGZI9e3Y1zNOlp0hpEvbZU6TsY0tHleThw4dqmDdmzBg5cuSIa+vYsaMULlxYvcc5TKFPgCIV+jZ0ZAkOHz6sYqIQF+VrQ6+KKfQJUKRC34YsgRsBDvfcYNjkJUXqLwz59OlTOXHihNy4cUNevnwpP3/+/Itv8RQzCFCkzKAe3GtSpHzwPXTokAwePFgKFizodTiBuJwcOXJI8eLFpWbNmtKqVSvp3bu3jBo1SmbNmiWrVq2SXbt2yZkzZ+Tu3bvy5s0b+f37t4+r8eOYIrBs2TJBYCeTfQhQpP635ZMnT2ThwoXSqFEjSZw4sUuYsA5sypQpsn//ftmwYYPMnz9fJk6cKAMHDpROnTqp8ytUqCAFChSQTJkySfz48V3f9ZwriRMnjqROnVpy584tpUqVkrp160q7du2kX79+Mm7cOJk7d66sW7dO9u3bJ+fPnxdM/L5//94+tY0lIYFoEHC0SB04cECJTf78+V3CAqHp0qWLbN68Wb58+RINpKK+B9G7cuWKYIJ369atsnjxYpk6daoMHTpUunXrJk2bNpUqVaooT1S2bNlc1/cUNrxPkCCBpE+fXvLlyyflypUTxAZ17txZBg0aJJMnT1biivyi93f58mV5/PixfPr0KVp555dIwGoEHCVSmE+aN2+eNGjQQN34WhDQE8LNjhvczPTjxw958eKFmvvCHNj27dtl+fLlgnigkSNHSq9evdSwEsPLEiVKSIYMGfyKW5IkSSRLlixSqFAhqVy5sjRp0kQJJIRy2rRpsmTJEtm2bZscO3ZMrl27Jph7i64wm8mN17Y3AduL1MGDB6V///6SN29e1w2dMWNG1RPZtGmTfP782RYWxpwX5r7Onj0ru3fvljVr1sjs2bNl7NixajjZvn17qVevnhQrVkxSpUrlYqGF2n2fPHly9USBokWLSvXq1aVly5bSs2dPJZQQzJUrV8rOnTvl5MmTSlCfP38u379/twVHFsJ6BGwnUljLNWfOHDXfEy9ePNfNWL58eZk0aRIfiOZRBz98+CCPHj2SixcvCoa/GzdulAULFihWGE5iWFm/fn3lQEiWLJmLp7uo6dcQv1y5cknJkiWldu3a0rZtW+nTp48SSggmhFM7E27fvi2vXr2ip9TDHnwblYAtROr48ePqZsCEtL5hMBRC9DEmuz9+/Bi15Pzknwh8/fpVDQ+vXr0qR48eVQt8MXzEMHLYsGHSvXt35fXMkyePJEqUyGUXbR+9R0OSLl061dMtW7asEkTYDY4JOCjgqFi/fr3s3btXzp07J/fu3aOn9J8sF3pfDkmRwrwJWnu01rqyY49KPmHCBLlw4ULoWcIhOUaMGeYGb968qYaLO3bskBUrVsjMmTNV+AY8ppg/Q3gHvKHu9nV/DQ8snBwIEYEHtnHjxtK1a1cZMmSI8sYuWrRIMJxH7xD14cGDB/SUhmgdCwmRwgQy5loQh5QzZ05XxUULjBXwaGkxbGGyN4G3b9+qnhR6VHv27JG1a9eqof2IESPU0BKNVObMmV31w13U9GsMWeFNLVKkiFStWlWaN28uPXr0kOHDh6teILyw8MbCK6s9peyJm1uvLCtSaHGXLl2qeke6gmFfpkwZGT9+vIojMhcdrx4qBCAyCMvAM9DhSEEPC15eBOtCpOApTZs2rV9xwzOr0EDi3Fq1aknr1q1Vowmv6/Tp0wVBpPSUBqdGWEqkUIkGDBiguvpamNKkSaPmKxDkyMDG4FQC/qp3At++fZNnz56p8AyEaUCEMCxF8C2CfvG0Baw80HXVcx83blxB/cW8XOnSpZV3FcG7iIjH0xuwMgGeUgx59bIrekqj2sJ0kVq9erXUqFHjD0PDoIjARrceCW50VBYmEggFAr9+/VKey1u3bsmpU6dUzw2BvAjjqFOnjgrKTZo06R913l3gEiZMKAiTQZAxYvgQvAtnAkJpMIqA91p7Sk+fPi24jp09pbEuUtevX1dR13hYmTYMWhu0MACPeQfPhK45oreZSMDuBBBCc//+feVUwP0ADyccAtWqVVPhHf6WXUH4smbNqv4xB84HOBOwegKhJN48pYire/36teXXlMaKSCH2BoGEWpSwx9o1dHkxIW6UMEGK7jYTCZCAdwJYBoW1npjwx/wYngYBpxJ6YkbLrvRieQTvwpnQrFkztTJBe0qxptXTUwoxja0UFJGCQuNpAHAja2HCwto2bdoIhneIjg4kYS4A3hwmEiCBmCWAlQJ37txRcWgQI8S44Yke6EQYLbvCPY3gXTgTMGXTokWLKJ7SLVu2/LOnNMZFCsF9Wpi49/3USLIhGyfWgUqVKgWssjEuUvDAYRjHjQxYB1gHvNWBQFUqxkUq0AzwfBIgARLwR4Ai5Y8Oj5EACZhOgCJlugmYARIgAX8EKFL+6PAYCZCA6QQoUqabgBkgARLwR4Ai5Y8Oj0WLANZgwtXsufFfXKKF0/Ffokg5vgrEPAD978KIenbfEAnNRAKBEqBIBUqM5xsSiIyMVE8HMDyRJ5DAXxCwhEhhzRGGCP4S1gpheYwODvO2dsjbZ/5+k8eCQ4D/Ihwcrk79VdNFCkMAPFAMj4D1lfQ5eHICzsPmLmo4jvkOvajS1+/w89ghQJGKHc5OuYqpIoVV2liBjefl+BIpDB2wxgl/peQtoReGm0InvQpcv+c+9gnAHp7r0jCJ7t6wxH6ueMVQJWCaSKHCRkREqMdL+Gt50XtyFyFP0BAlCJlOGPL5O1+fx31wCcAuOuE1GiH0mDkk11S4/1sCpomUewZ9iRSEDC0yekv+EnpkuvJj2Gd0vr/f4rHgEIB9YEt6+ILD186/ammRQoXWIoXHp+q4G/eeE4yDGwDihI1DCutWV6NesXVzzpyZScDSIoUeFoYIqNyYk8KwAZ9hHotDOjOrTeDX1j0pzwYm8F/iN5xGwPIihZ6UZ+9Ie/ucZqxQKS8aEPchN16jF4zGRg/LQ6UszKf5BCwtUug9hYeHR6GEHpU38YpyIj8whQAcIrCP++YZNmJKxnjRkCRgaZHSYuTZ+vr6PCQtYNNMo/cEO2HztJ9Ni8xiBYmApUUKZfY22YoJcnzORAIkYH8ClhcpHcwJ7x6WxOCfYzGMQAvNRAIkYH8ClhApCI6/+BlMnCMWCvMamJT1nEi3v5lYQhJwLgFLiJRz8bPkJEACRgQoUkaEeJwESMBUAhQpU/Hz4iRAAkYEKFJGhHicBEjAVAIUKVPx8+IkQAJGBChSRoR4nARIwFQCFClT8fPiJEACRgQoUkaEeJwESMBUAhQpU/Hz4iRAAkYEKFJGhHicBEjAVAIUKVPx8+IkQAJGBChSRoR4nARIwFQCFClT8fPiJEACRgQoUkaEeJwESMBUAv8BHAdCnbFTSs8AAAAASUVORK5CYII=[/img][br]Is Tyler’s triangle congruent to the triangle on the Data Card?[br]
Did Tyler do anything that didn’t match Jada’s instructions?[br]
How could Tyler have made a more specific request for 2 sides and an angle so that his triangle was guaranteed to match Jada’s?
IM Geo.2.4 Practice: Congruent Triangles, Part 2
Match each statement using only the information shown in the pairs of congruent triangles.
Sketch the unique triangles that can be made with angle measures 40° and 100° and side length 3.
How do you know you have sketched all possibilities?
What is the least amount of information that you need to construct a triangle congruent to this one?
Triangle ABC is congruent to triangle EDF.
[size=150]So, Mai knows that there is a sequence of rigid motions that takes [math]ABC[/math] to [math]EFD[/math].[/size][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAARsAAACeCAYAAAACJ67+AAAb6klEQVR4Ae2dCdhVwx/HlSWKf4mUENlFRfa9tBMJkTxKQiQV2UolLUS02rXYIkvJnhKFspaSFmnPkq20WFrn/3zm/5+3+9737u/ZZu7v9zz3ufeeM2fOzHfmfM8sv2UHJSIICAKCQAAI7BDAPeQWgoAgIAgoIRvpBIKAIBAIAkI2gcAsNxEEBAEhG+kDgoAgEAgCQjYew9y6dWvVqVMnj3OV7AQB+xEQsvGwDV977TW1ww47qHLlynmYq2QlCLiBgJCNh+144IEHqqZNm2rC8TBbyUoQcAIBIRuPmnHUqFGqbNmy6sMPP9Rk8/XXX3uUs2QjCLiBgJCNB+24Zs0aPXW6++67dW5MpSAdEUFAENiOgJDNdixy/gXJMIUyAtkMGjTI/JVvQUAQUEqU+orbC8yohmmUkbPPPluZUY45Jt+CQL4jICObYvYAtroZydSuXbvgw24UC8UigoAgsB0BIZvtWGT9a+nSpZpoIBxGMubDyIaPiCAgCGxHQMhmOxZZ/4JkEpEKpCO6NlnDKRc4joCQTY4NbLa4E+06GeW+HLOWywQBJxEQssmxWVNNlQwRia5NjuDKZU4iIGSTY7NCKKzZJBJ2qDjPt4ggIAj8DwEhG+kJgoAgEAgCQjaBwCw3EQQEASGbFH0ALeCzzjpLNWrUSI0ePTpFSjklCAgC6RAQskmCUPfu3bUODQp75vPcc88lSS2HBQFBIB0CQjZJEKpYsWIByRiyqV+/fpLUclgQcA8BRva9evUq8sm1pkI2SZArVapUEbI59dRTk6SWw4KAewjwkq1Zs6ZWXDWqHomUWDOtuZBNEqRatWpVhGz69++fJLUcFgTcQsDoiiVT78iltkI2SVB78sknC8imZMmShVxIJLlEDgsCziCAyQ3O4LwUIZsEaP7555/qxBNPVIxutmzZokaMGKGJ5913302QWg4JAu4hgNeC4kyZEiEiZJMAlX79+qnddttNxZob7LfffuqSSy5JkFoOCQLuIYAzOEY3XoqQTRyac+fOVfvuu6+66667Cp156KGH9Ohm+vTphY7LH0HANQQws2Fx+Nhjjy3w0YS/plgHcbnUWcgmDrUbbrhBHXnkkeqPP/4odGbbtm2qdOnSqm3btoWOyx9BwDUEjNcC45/JfLNoXBwRsolB77333tOM/sQTT8Qc3f7TKPrNmzdv+0H5JQg4hgDkEutT26vqCdnEIHnBBReoBg0axBwp/JPRDsPLLl26FD4h/wQBhxBgYdgPt7ZCNv/vJCNHjtREkm7H6cYbb9Rbgj/++KND3UuqIghsR4Atbz+igwjZKKVWr16tatWqldF6zOLFizUp9e7de3vryC9BwBEE2IFl9F7c9ZlEcAjZKKX69OmjypQpo9iJykRatmyp57QbNmzIJLmVacwiIR0v9oPfZRF3EUBj2Ostb4NW3pPNnDlz1H/+8x91zz33GEzSfn/11Vf6ARwyZEjatLYmoMNhF8MbLvbjpfq6rdhIuXNDIO/Jpl27duqYY45R69evzwrBc889Vz+MWV1kUWIWCWUUY1GDWVDUvCYbFoOZIuSirDRp0iR97TPPPGNBM2dfRHDxY5Ew+5LIFV4isGLFCsWIfODAgWrhwoVeZp02r7wmmyZNmqjzzjsvLUjJEuByAk9+romfi4SuYWVTfT7++GNthhO7Bvfmm28GVoW8JZvhw4frkcnkyZNzBvvll1/WeYwfPz7nPKJ4ISO92A5pfvuxQxHF+rtaJtzbmrY036effnpg1c1Lsvn999/VUUcdpTBNKK5g2nD++ecXN5tIXd+pU6eEi8MSmiZSzaQ2bdqk0PdiJDphwgT17LPPqgEDBqjbbrtNeyyAXI477jhVuXJltdNOOxUhGghn9913D6xSeUk2uDrcY489PJmzGr83U6ZMCazR/L4Ru1AQjkjwCKxbt06hy/XZZ5+p119/XT311FOqb9++qmPHjuqyyy5TderUUdWqVVN77bVXQvKAQHBpW6NGDVWvXj11xRVXqFtuuUXdf//96rDDDityTePGjQOrZN6RzaxZs1SJEiXUfffd5xnINO6VV17pWX5hZ0SHzWXRPOxyR/H+GPD+8ssvWoeLFxJT74cfflj16NFDsRN64YUXKtb+DjnkED3KMNOb2O+dd95ZValSRftYYp0RY+Bu3bqpwYMHqxdffFF98MEHOn9G7IkE/0xmCoV2sMmbPL/88stEl/hyLO/I5tprr9Ws/++//3oGKG8NGjDW/41nmQecEesyrtTFL+j+/vtvtXz5cjVjxgw9fSHqBi5Ibr/9dnXVVVcpRgtopO+///4KojAPd+w305dDDz1UnXHGGeriiy9W7du317pejz/+uEKhElcmixYtylolI77Os2fP1iMh7g1BIUy53nrrLbV169b45L7+zyuyefvtt3XDP//8856CunHjRoWD9A4dOniabxiZsd1Nx4z3qu/64jAmK99995365JNPFAv+TF/uvfdePZ28/PLL1TnnnKOOPvpoVaFChYTkAWbly5fXaerWrVswfcFvNaPEd955R5PTDz/8oDZv3hxI07LTBKlRNkgsbMkrsmEOy7DVD7nzzjv19GzJkiV+ZB9YnmgOo9AX/7GNbMziKW/2999/X40ZM0YNGzZM9ezZU11//fXqoosuUuzEMLpAg5wHMtEHR2ossqLEefXVV6uuXbsWmr58++236rfffgusfTK90SOPPKLrs88++2iiy/Q6P9PlDdmYhdyPPvrIFzyZl9NZ4z38+XKzPM3ULJ5+/vnnehrAiIHdF6Yvbdq00TpTJ5xwgjrggAP0SDMReTACxVfLKaecol887EgyinvsscfUuHHj1LRp0zyZvoTZROBB3cECMoyK5AXZ/Prrr3r+7PcOCwt+7BIwJBdJj0D84umrr76qH3oMY9l9YfrCaLR69eqKN3Qi8uAYO4uHH364VrBkx4Z2ZgMgdvqycuVKvVWcvlR2p2jRooXGiZEb5BwlyQuyYejMKvyyZct8xZ45P52ft22UhZHBTz/95EsREy2esg7E4uR1112nmjVrphdFIYfYnZF4Itl77721zRpRSNnp422Niv0LL7ygUMSM6vTFF1AzyJQF69NOO033v86dO2dwRfBJnCebmTNn6gZ48MEHA0GXNyvrAEGv9GdSOaYJlSpV0njwcDN6yEQSLZ4yckB/g3A37L4wZGd6suuuuxbkH0sgxN5Cuez444/X051rrrlG4WaVbeCxY8fq6cv3338fubdxJviEnQYzBKJ/gDeEHFVxnmywXMZLPEP2IARlLBqdNaKoSaL45TzwsYunbME2b95cK49hDQ85oZcUSxzmN+FuqlatqvVEGLZzLVMgdnLYCcEVR75MX8Jqa3ZWaQ+mkq+88kpYxcjovk6TDR2ehkCRKkjBj/FJJ50U5C3T3suQoCGKZN9MbY444ggdwoP5/80336y1T7Funzhxovrmm28Ua2Ai4SPA1jztiOkNU+Ooi9Nkc/LJJ+s1gqAbAaUpOsFLL70U9K2T3o8RRiKCYR2Ftaa1a9cmvVZORA8BNiNoz4YNG6qff/45egVMUCJnyYatTBqDN3oYQvjeVJEawigT+iXxhBP0qC+Mert0T0wPWCOjHdGGt0mcJJtVq1bpnY4wQ65gs0KHIBZVlOTpp5/WOins7rB7gX3MggULolREKUsSBJjCosVMv2JtzDZxkmzYZi1Xrpxv27uZNjJWtpdeemmmyQNPx06dsc9hy1okughgy4TpAa4ibPUO6RzZGGfkQ4cODb3nPProo/otFNZULhMA3njjDbXLLrtoW55M0kua4BEwpgcHHXSQLyFWgqqRc2TDFiwWt1ERlNOiPrc2ndlYBUcFOymHUnfccYd+YZ155pnaz43NmDhFNjgbYj4bJTed/fr102WaP39+pPsJBoZgFwXr4EgDFWDhMNegTXCAFZSluJ/Vc4ps8GCGb5AoCYHsdtxxR+2qMUrlSlQWzALo3OlCECe6Vo55hwAREIzpAd4EXBFnyMZMBVj0jJrgExYnSlHXh8BVAm4nUX3PNDpo1LC2vTyYHuB0C9Jnzc8lcYJscPqM7Q0PdRQFh0l0HnzJRl3wNsgOFW9WUfQLtrVGjx6t+wlmJew+uSZOkM1NN92kvaRF0YmR6TAYHtKJbNhiZoeKLVbWDESCQcCYHmDQij6Ni2I92XzxxRdWDDlxicDoBm9xNojZtmc3RMRfBIxmN14k0RB2VawnG/yd8DawQVi8Js6ULcJWuItrB1HBn2kq7kbBOFN3H1Epey7lsJps8EJPQ+HI3AbBmTblxRu/LYK/Gsrs4hpCmG0wZ86cAtODoHwthVlf7m012eBrFt8rNgle+ll8tUWIRUSZcfyN83CR4iMAceN/Bkfr+WQIay3ZmFhNvCFsEuNjh0VYW4QdKpxk4SQ8WSA0W+oSdjnNWhgGlVE2Y/EDJyvJxvhmwXLZRsGc4rzzzrOq6JAkHvuibFgadUBR0GNKig8av3xARxkDK8mGqIPYHNmqB8KaDZ1u6tSpUe4bRcpmfARFVZ+pSIEjdMCYHqACka9iHdkY95a22/AwLbExPjhxsSBKW7bww36wMT0gGB6Y3XPPPWEXJ9T7W0c2rBvgBc92wQUGHdDGRVezQ4Xhq0hyBNh9xPQAFx7EsMp3sYpsjCf5qHm/y7UT4eDLRv0KFokJz0vgOPwHiRRFwJgeHHzwwTrOVdEU+XfEGrLZsmWL9r5HXCZXpHfv3np043fwPD/wmjVrlo4TxSgTN6wi2xEgphaj1rPOOksRC0vkfwhYQzZmrYBIAK4Iqul0yh49elhZJfRFKP8ll1xiZfn9KDSxw8EEHzQbN2704xbW5mkF2RBalAZ0ybeH6THEZSLY25o1a8whq75ZqKdtiI6Zz0JcbWN6IPZkiXuCFWSDTRHrA//880/iWlh8dOnSpfphtVll3Yw6hwwZYnFL5F50FEuJHgrp4ldJJDECkSebDz/8UDdiFMPZJoY0+6PoDeGwymYxXv5effVVm6uRddmxy8P0AHMOFB9FkiMQebJBrZvIli4L5gC8FYcPH25tNf/44w+FU26ULfNFDd8oORJqmQVzkdQIRJpsTGNOmjQpdS0cOIsvE4biNgs6Q+iVHH/88QqTEpfFmB4QzWP16tUuV9WzukWWbDZt2qQdheeLtzgzXXzllVc8a9wwMmJawSitWbNmatu2bWEUwfd7tmzZUtfRRh0p38FJcQNfyQZ/M7169Sr0YcqQidCQdNrFixdnktyJNCjKoZthu5gdqs6dO9telULlZ7RmTA8GDBhQ6Jz8SY+Ar2RTs2ZNrWl69913q9atWyv+QyDpVLcXLlyo0+Vb0DTjDMyFaaPZobJ5ly328cH0AP9JaH2PGTMm9pT8zhABX8kmEbE0bdpUHXvssSmL16BBA1WpUiWF1nC+SY0aNRQYuSBmuvHiiy9aXZ0XXnhBv/yqV6+upk+fbnVdwiy8b2Rj1iDip02McsqWLVukzsTL6dKli2LBDZKyeWemSOWyODBy5Ehdfxy52y4snOKVsHz58or2tVH69++v26Nx48aKkDwiuSPgG9kMGjRIN1Js0dCSJTg6U6pYMQaWkIz52OTJLrYuXvxmuN6mTRsvsgo9D8KSVK5cWY9mlyxZEnp5simAMT2Ieqz2bOoUZlrfyAZCgVjMAjGLhcx3O3XqVEQ1n+gIhmTMd7169cLEJdR7Dxw4UOPhih2Y2aFiesguY9QF0wM8KdIXMZYV8QYB38jmwAMP1FbB7LDw4X/t2rVV/LSKauy5555FyAbT/HwVgsijleqSvdETTzyh27hDhw6Rblbie6HvVKpUKcWUVsQ7BHwhG6ZLvBXYXYkV3myMduIFv7ZmRGO+iY2NT5B8lZ49e2pMfvnlF2cgMIpwuGCIorzzzjs64gHhh13YEYwaxr6QjVkcxsgwVsxxvmOFuTwq34ZomFbVrVtX/8dUIdFoKPZ6F38TShg8bIgPng3+LVq00PWKWuwso63O6NuV6Ws27RJEWl/Ihh0npk3xkmjRODbNzJkzC7nJHDt2rA5yz0OHseK///4bm9z538QwZzrlUr3ZocK1KzuSH3zwQSTasGvXrpoAMSZ10bNAJED2K0gd06V4XRFGMywQx+9EZQKEiREF6TzwwAOZXOJEGry8UWfX3BawQ1WxYkWFThEKnGGK0QWCcET8RcCXkQ1vLR6S2A/HGPHkKvi9JQwGeeKOIV/M+XnbVqlSJVfYInsd6yO0ZZMmTdRff/0VeDnRmTnjjDN0GVwj88DBzPCGvpANo5j4T4blSZsM9wXMq+mobI8vWrQo7TU2J0C5j7qii+SamOiQ7dq1C7Rq06ZN0wTOSyuf9bkCBd2vaVQQleDho7PwILpufcvbP52JRxCY+3EPoprShn369PEj+yJ5YjrB/fJ146EIIAEe8GVkE1T5sZ1iakbnQS+CHQUXZeLEibqOOBh3UZo3b67r57deizE9wEE7zr5EgkXAarIxUBEKBW/2kE61atXUlClTzClnvnFtUKdOHWfqE1sR9LIICcPOm18xwdq3b6/7h2tuL2JxjPpvJ8jGgMw6EcNjSAeDzl9//dWcsv775Zdf1vWy1aAxXQPgNLxChQoKN7Bz585Nlzzj8+vXr9eL0PQJV9xdZFz5iCV0imwMtk899ZS2NKaD4VfFFWHURqQJV8XEoWrYsKEiplZxBdLCLQRW5y+99FJxs5Pri4mAk2QDJnRWs/hIGBgXTB+IMAGBMgpwVR5++GFdx7Zt2xarimyto26BLg+7TyLhI+As2RhoMawzPnJOPfVUhZayzYK7BvSNXBb8GkGq2IflIsYtKZbbK1asyCULucYHBJwnG4MZbzrecnRiTB9sVUs32tSuP0RMF2krrMWzEWN6ELTuTjZlzNe0eUM2poGHDh2qw92WLFlS8eDaJn///bcuP1NEl4VpcK1atVTp0qUV/nAyEbMj6ZrxaiZ1tyFN3pENjYKqOkaOvDkPO+ww67RIzdt77dq1NvSxnMuIDRWLu0cccUTKIHC0JwHyiJn+9NNP53w/udBfBPKSbAykmD7gWxbSYQcEw0cb5KefftJljqpfGC8xfP3113VdzznnHIV9XLzggBzbMV4a77//fvxp+R8hBPKabEw7EJ8ah0mQDiMeGwT/uHg4zAcZMmSIbptWrVopgvixjoNNnDE9gIjEB030e4KQzf/bCOUvs/jKQ4yRYJRl3rx5+gHMdgE1ynVKVbbrr79e15cXQuwHAgrDajxVWeVcYgSEbOJwWbBgQYErC2JWR9n0Aa93+eKr2bgUjSUa9GhE7EFAyCZJWzH/N64s8JEcRV/ArFfw8GHK4LrgTiSWaMxvieVkT8sL2aRpK3Y3jCuLKJo+NGrUSOGz2XUxO3CGZPhO5DzfdRxsrp+QTQat9/PPP+v4V3RwfCtHyZGVicnk+k4MLiHQu4klmyi1QwbdKO+TCNlk0QW++uqrAlcW7IDMmDEji6v9S4oD8fr16/t3gwjlPG7cODVixAgVH7kjQkWUoiRBQMgmCTCpDo8fP77AlQWhWdHqDVMwMuWNDxmKCAJRRUDIJseWwbYKC2U0XMuUKaPwAhemoGV72WWXhVkEubcgkBIBIZuU8KQ/idaxcWWBoScar2EIEQIY3diiBZ0tRgQqZHfQfIghL6YJ2aIYbnohG4/wRx/HuLJo1qxZKA89fntQfnNRTIBDfE7zIX485IojeNyKikQfASEbj9uIHRLjyuLWW2/1OPfU2fXr108/gC65QzU1JrghBBMrjHYgnFwCH8bmI7+DQUDIxgecidPNGg5WyDi7Csr0Yd26dWrnnXdW3bp186FW4WZZs2ZN1alTpyKF4BiEIxJ9BKSVfGwj3rzGlQUuEHDI7rcwmtpxxx3Vpk2b/L5VoPlDKKNGjSpyT45xTrbCi0ATuQNCNgE0CY68jSsLhvyrVq3y7a7Lly/XD9+AAQN8u0fQGUPSyQgl1bmgyyn3S42AkE1qfDw7u3nzZoVvXFxZ7LLLLqp3796e5R2fET6KCYviirAgnMzo0gQpdKWuLtdDyCbg1mW43717d/2mPuqoo3yJ+jB79mydP5q2LkjTpk2LLA6benGO9RyR6CMgZBNSGxFsrk2bNpoUiALgtfYvIWYPP/zwkGrn7W2xR2MEEy9mN4ptcZHoIyBkE3IbjRkzpsCVRceOHT0zfZg6daomMmyJbBZ0aFiviV9c5zg6NjKqsad1hWwi0FY8OISGxZUFay24wfRC6tatqzDStFlee+01TTZGcY/vwYMHq3LlymmiYXQjYgcCQjYRaiciXRL4njc5McvZxSqOGGfhUfY2mK5+ZgEYTMzHTKsMAaXLQ85HAwEhm2i0Q6FSvPvuu6p58+b64WrZsqVauHBhofPZ/MG1KdvutgojF6ZQ5iMEY2tLKiVkE+G2Gz58uB7hlChRQvXo0SOnkmKsyIiAHSoRQSBMBIRswkQ/g3uvXLlSewnElcUhhxySk6Uz1xEtUkQQCBMBIZsw0c/i3p9++mlB1IcGDRqojz76KOOrWVBldANxiQgCYSEgZBMW8jnelyBtxvSBQHX4R04nW7duVXvttZfq0KFDuqRyXhDwDQEhG9+g9S9jAuoxWqlevbpW42fbPJ3gbIrRDdeKCAJhICBkEwbqHt1z/vz5CitvXFkQeSCVAh/RCUqWLKl69uzp0d0lG0EgOwSEbLLDK5KpJ02apIiOyciFLfNkO0/o8JQqVSqSdZBCuY+AkI1DbYxvF/zmQDqEq42Pgb148WJ9LhdbIjR5r7rqqgIfwBCX+JBxqPMEUBUhmwBADvIWLBj37dtXVa1aVVWpUkU9+eSThW6PP51KlSoVOpbqD0p02CBBYFyLRi8fbJLi7ZVS5SPnBAEhG0f7wJdffqmdn0MSderUUZMnT9Y1xbqcY88880zamhuigVhkFJMWLkmQBgEhmzQA2X6a6U+TJk00weBUa9myZXrrHINP1nmGDRuWtIqMYHBaJUSTFCI5kQUCQjZZgGVrUiJ2QirHHXecKl26tNp77701+TDC4XPppZcmrBpEk8jJeMLEclAQSIOAkE0agFw6TQA7tI8NycR+x+9gGdcO4sLBpR4Qbl2EbMLFP/C7G5eksUTD7wkTJhQqi3HtUOig/BEEioGAkE0xwLPxUnRy4olm9913Vxs2bChUHaZP+I0REQS8QkDIxiskLcoHLWJDOGyD45o0XmRkE4+I/C8uAkI2xUXQ0uuJnjlz5sykpTextUWXJilEciJLBIRssgQsX5KjY8M0CoW+2K1vjsf+zxc8pJ7FR0DIpvgYOpsDO1EQDlOugw46SDsZ5zdTLBFBIFsEhGyyRSwP0zOVwu6K7XDZCs/DDuBRlYVsPAJSshEEBIHUCAjZpMZHzgoCgoBHCAjZeASkZCMICAKpERCySY2PnBUEBAGPEBCy8QhIyUYQEARSIyBkkxofOSsICAIeISBk4xGQko0gIAikRkDIJjU+clYQEAQ8QkDIxiMgJRtBQBBIjYCQTWp85KwgIAh4hICQjUdASjaCgCCQGoH/AmWP1dbdw4F9AAAAAElFTkSuQmCC[/img] [br]Select [b]all[/b] true statements after the transformations:
A rotation by angle ACE using point C as the center takes triangle CBA onto triangle CDE.
Explain why the image of segment [math]CB[/math] lines up with segment [math]CD[/math].[br]
Explain why the image of [math]B[/math] coincides with [math]D[/math].[br]
Is triangle [math]ABC[/math] congruent to triangle [math]EDC[/math]? Explain your reasoning.[br]
Line EF is a line of symmetry for figure ABECDF.
Clare says that [math]ABEF[/math] is congruent to [math]CDEF[/math] because sides [math]AB[/math] and [math]CD[/math] are corresponding.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAOgAAACACAYAAAABDiVPAAAUYUlEQVR4Ae2dCdRVUxvHo1WRJg20QnMZYsnQKxkqGsVqkMjUIIWKKCwZorxZpDJnSCUaSGKZSikSIikRq6KUkjKElNKwv/XbfbvOHd73vcM595697/OsddY599xz9tn7/+z/fp49F1MigoAgEFoEioU2ZhIxQUAQUEJQyzPBkiVLVLNmzWKOm266yfKUSfRBQAhqeT4YPXq0KlasmBoyZEjEMWPGDMtTJtEXgjqQB7p166aaNm3qQEokCfEQEAsaDxWL7p188slK3FmLFJZkVIWgSQIWpse3bNmi3VtxZ8OkFX/jIgT1F8+MhjZv3jxN0DVr1mT0u/KxzCEgBM0c1r5/iYYhGoiiD4gr4gYCQlCL9di+fXtFHRRCeg+LkyRRj0JACBoFiE0/a9SoobtWbIqzxDU5BISgyeEVmqepd+LaijsbGpUEEhEhaCCwBh8oLbcQlJZcEXcREIJaqlsaiHBxRdxGQAhqqX4Zg8sh4jYCQlC39SupsxyBlAlK4wR1IFwtEUFAENiHgOGFt2+6YcOGKtXRXikTlP638uXLK/riRLKHwFNPPaVOOOEEVa5cOdW1a1e1cePG7EVGvqzM7CKgoKUdwsIRCDt+/PikEUqJoHwIcjJIW2ZSJI25by+8/vrrWvHe0vr888/3LXwJKHkECppdBE9q1qyZdIApEdR0kFNaVKhQIemPygvpIbBz50719ddfq+bNm8cQFLJOmTJF/fzzz+l9RN5OCQG4EW92EUYN3STbsJc0QalzYj3pfzP+dkopkZeKRACSffDBB+qZZ55RN998s7rgggtUnTp14pLSa0XNNW5vXl6euuqqq9T999+vpk2bppYtW6Z27NhR5LflgeQRKGx2keEK52QkKYISASym8aXNR5MtFZKJoOvPbtu2TVvD6dOnq/z8fHX11VerM844QxeChmicIVujRo0iyPbcc8/FkLVt27a64Hz66afVgAEDFL9r164d8xz3+I9nxowZo+bOnavWr1/vOtyBps/wId7sIvNfoATFdENQSnVzkHmS/WigKIU08HXr1u23hrfccotq165dXGtYq1Yt1aZNG+0mGeIU5q5iFSHbQQcdpMn233//xUUAtxjr+corr6hhw4apK6+8Up1++uma+PEKAv7nOZ5funSp+ueff+KGKzcPIGC8ywN3Dlx5G48O3C36KmELasZ+epVprvm4iFJ//fWXrmNgDYcPH65oMMAaUqgZrDiXLVtWk+OKK65QQ4cO1ST46quvUnY977vvPlWiRImUVbBhwwb1/vvvK1qEKYRbt26tKCi8cebaW3jw7Jw5c9TatWtT/q5rL9IQVFCvBr0eBf1XGA4JE5TMxkeihUjlWl/o6tWrdeZ89tln1cCBA7U1rFu3bkyGptWOzH7jjTeqJ598UpMgCDcyXYJG69T8pq6K9Xz55Zd1QXL55Zer0047TRcwXvJ6CxysLs8vXrxYF1gmrFw40zYTjwvGeqbSF5oQQQvznyEoh2vy22+/qUWLFunM9sADD2hr2LhxY3X44YdHEJHMSaYl80KUqVOn6kz977//ZgySoAhaWAJ++uknXUhR8PTv31+1atVKdyN4icu1KaSwzDw7a9Ys9cMPPxQWtJX/GQ8zurpnWm/jtewmktCECFoYCSkxbCXorl271IoVK9TMmTO1e4c1vPDCC1W9evUiSGgyGpmQzPjEE0+o2bNnKzJpGCQbBC0o3du3b9duPgXVvffeqwdPUICVKVMmAlN+cx83n/hPmjRJff755+qPP/4oKOhQ3zezi0izOSicyDvxrGqiiSmSoJQMEDC6ZDAfoIQIO0F/+eUX9cknn+hMgAvWvXt3deaZZ6qKFSvGZJpTTz1VZypApj/xyy+/VGS6MEuYCFoYTjSUUbA9/vjjql+/ftrq0m9YkNWlMHzsscfUO++8o1auXKn27t1bWPBZ/c/wwBgzqoS4tulOByySoFlNdRIfx6Vcvny5evPNN7VS6T646KKLVP369WMyAJmiZcuWOpOQAd577z2rGztsIWhB6qSriTrr5MmTtbVhyCIFZUFWl+rEPffcoyZOnKgL3s2bNxcUtPX3rSMojSzz589XEyZM0MqkE75JkyYx1vCwww7TSr7sssv0c7hQZAIXuwtsJ2hhLPrxxx91vZWCFKtLwVq9evW4hS5VkBtuuEGNGjVKF9TfffedohpjswRK0D179qgFCxYoWj2Tkb///lvR7YBfP3LkSK0YRtHEs4YoC6X17dtXW07qkyg1l8Rlghakx61bt6ovvvhCV1uwphTEp5xyiqJg9rrMpqDu0qWLuvPOO/Ugm48++iilSQUff/yxWrVqVUFRCuR+YASlL7By5cr7werZs2dMAqjfMoJl7NixavDgwbruR79hpUqV9r8H2KVLl9bgowSUgTWkhRUliSjdyJJOP6hrGJKvKKgfffRRXXC3aNEirtWlcGdyQZ8+fdSIESO0QWCMc/RQSOrA1apV258nGcSRKQmMoFWrVt2fIFOide7cWYOBKxKv3/CYY45RgImbAriAnKz1zRRwYfpOLlrQVPDHM6Ngf+mll3RBf+mll+qCHwNg8qgxCPT5X3zxxer2229XVapUififZ3C5MyGBEBQQvAn2XgMGE1gB5+6779Zg0bzOKByR1BAQgqaGm/ctDMG7776rDQMGAkOBwfDmXe91p06dvK8Hdh0IQTdt2hQ3Yal21gaWekcCFoIGp0gmwDPO2UtOrm+99dbgPuoJORCCEj4Dwr2JYjaGzPb3IO/jpRDURzDjBNW7d++IvEz1LVNVr8AISjppKGIcKv2RkJU6pYj/CAhB/cfUGyJtJ/TJ0rfOsM/CZhd53/PjOlCCeiN47rnn6v5K7z259gcBIag/OMYLZdy4cdq4sLxMNiRjBKUPCSvKzH4RfxEQgvqLpwmNIaKMp+3YsaO5lfFzxghKyqhYlyxZUo/oyXhKHf6gEDQY5V5//fXaqGSzhyGjBN29e7eeKZLKxNVgVOBGqEJQ//XImG48PvrjsykZJSgJffXVV3XCWQhLxB8EhKD+4OgNhfWfGLCfbck4QUkwQ6WOOuooWaTKJ+0LQX0C8v/BMH8T68kaTtmWrBCUic4MYu7Vq1e20+/E94Wg/qlx4cKFmpz044dBskJQEs6kXUqp1157LQw4WB0HIah/6mPW1BFHHOFfgGmGlDWCEm9mEjAul2lpIqkjIARNHTvvmyxlg9GggSgsklWCMkgeQJhqJpI6AkLQ1LEzbzKHGMvJDJYwSVYJChCQE5IyiVYkNQSEoKnh5n2LNYTIh2GbY5x1ggLS8ccfr1dF8AIm14kjIARNHKt4T7KOL+TExQ2bhIKgb7zxhgZIVqhPLXsIQVPDjbfYKqNBgwZ6k6nUQwnuzVAQlOT16NFDLwrt4qLGwalvX8hC0NQRHjRokDYO33zzTeqBBPhmaAjKwGTmjLKkokhyCAhBk8PLPM0GYLi2mZp8bb6bzDk0BCXSbJkHYKwZI5I4AkLQxLHyPtmsWTO9rIn3XtiuQ0VQwGGzIZbXzOTeJmFTSrLxEYImi5hSDz30kDYGb7/9dvIvZ/CN0BGUzYCxorJ+UeK5QAiaOFY8yTYSrJDAwnVhl9ARFMDMYGX2rBQpGgEhaNEYeZ+45JJLVPHixRVbToRdQklQQDvxxBPVWWedFXb8QhE/IWjiamDLEDw0NiC2QUJLUFbzBsj8/HwbcMxqHIWgicHPvjzsEn7OOeck9kIIngotQcHm2muvVaVKlVJsgiNSMAJC0IKx8f7DgtQU+t9++633dqivQ03Q33//XQ9e6NChQ6hBzHbkhKBFa4AtJiEnWznYJKEmKEA+//zzGljOIvEREILGx8V7Ny8vT9WpU8d7y4rr0BMUFJlEe/TRR6s///zTClAzHUkhaOGIs1s61pO9V2wTKwjKOEkApk4qEouAEDQWE3OH7QTZW4WNnm0UKwgKsCx4DUlp3RWJREAIGomH91e7du3UoYceGrPnp/eZMF9bQ1BAZM9GdlEWiURACBqJh/nF0q4U6ozxtlWsIujs2bM14HfddZeteAcSbyFoLKz0ABx55JF63avYf+25YxVBgdUsx7906VJ7UA44pkLQWIC7d++uC/MVK1bE/mnRHesIyjbmlStXVq1atbII5mCjKgSNxNds28AO7raLdQQF8IkTJ+rS0ZbxlEFnEiFoJMKM42adKxfESoICPJsCV6xYUW3evNkFPaSVBiHoAfjuuOMOXXgzcsgFsZag1C1ooWOfl1wXIei+HLB48WKdJ6655hpnsoS1BEUDbEcOSbO1+3FYcoEQdJ8mmjdvrsqXL69X6guLbtKNh9UEJfFsEXfsscemi4PV7wtBD+z149qYbesJalZmu+2226wmWTqRz3WCbty4US9h0rZt23RgDOW71hMUVPv166ddXfZ6yUXJdYJ27dpV63/VqlXOqd8JgrICIKNGzj77bOcUlEiCcpmg06dP1+QcNmxYIlBZ94wTBAX1SZMmaUU98sgj1ikh3QjnMkFr166tx2ini2FY33eGoADcsWNHvUTK+vXrw4p3IPHKVYIOHDhQF8our/7oFEHZ14Vuly5dugRChLAGmosE/fTTT7WuGZvtsjhFUBRlVgxnS7lckVwkaOPGjVWVKlXU7t27nVazcwRFW40aNdJ7buzZs8dp5ZnE5RpBH374YW09X3zxRQOBs2cnCcpu3bi6ubJ9RC4RlK3qDz74YNW+fXtnSelNmJMEJYGQE5JCVtcllwjaqVMnrddc2UfWWYLu2rVLVatWTbu7QlA3EJg8ebIm54MPPuhGghJIhbMEJe1Tp07NCYXmggVlq/qqVavmRIHr5a3TBCWhnTt31iRlU2BmvbAig2viMkEXLlyoaJE3S5jkQpXFmz+dJyjrolIXNUe5cuXUW2+95cXA+mtXCUp/ttEbZ3bEzjVxnqCDBg2KUDKKZkkMl8RFgo4fPz5GbyxAvWXLFpdUV2RanCdokyZNYhQNSSHuzJkznXB5XSLo8uXL1dixY9Vxxx0XV28uD+uLx1bnCXrdddfFKLpEiRL77+Hytm7dWrF/B4RlD0nbxGaCGkKyTEmDBg3264XV4L3urbnesGGDbepJK77OE3TlypWqevXqEcpm1j0ZgzP7veDymgwQTVimsoVdbCIoe3NiIaMJCe5t2rRRpGXWrFnas2H6oNEL58GDB4ddFb7Hz3mCgtjWrVt1phg1apRatmxZXBDJOOPGjVO9e/dWJ5100v6M4SUsGWfnzp1x38/mzTATlMXd4hGybNmyihUQhg4dqliBDx3FkylTpui1pz788MN4fzt/LycImooW2dWbhoo+ffoUaGHZioIBEdmWMBGUVQ3iEbJMmTJ6G0kmVoObjVWJbOhZCJog6liCCRMmKOq03rqS18LSgLF3794EQ/TvsWwSlCF3VBWiXdbSpUsrdhZjV7o5c+aobdu2+ZfgHArJWoLOmDFDN+zQuMPBIIRMNsFTt33hhRf0XjGsYm7qSl7CsqBZJiSTBGWwOp5FNCFp1MFlzc/PVxRU27dvz0TS435j3rx5ujClQF2yZEncZ2y5aS1BmzZtqmrUqKE4m2tIAnGzIbh2bEmBhfV2ERjCUteaP39+IFELkqDr1q3T6Yom5CGHHKIbdYYPH67mzp2rwtCYhu5r1qypC0vyBgd5wuZZTdYSFOBHjx4dkeEhasOGDSPuZevH999/r5ivSB2WdXujLSyu34IFC3yJnp8EZbkYhkX26tUrwpUvVaqU7o5isXAs1I4dO3yJu1+BmIENQ4YMifCk1qxZE/Hbr+9lKhwrCYrbQoaPdl9QDvfDKNTVyPi0EtevXz+GsFgilvFIRdIhKGvKMkuEeHnr1iVLltQ7yBEvXPUwtl4brEx+iC6wzf82n8OZm4tAFEXEIyI7cNsykXf16tV6JUL6YevVqxdBWPoDmVL12WefFYHEvr+TIeimTZv04PPoxi4Gb7Rs2VLXIenSYPaILYLO0b2LYiVBu3XrpusapoGIM3UPXNxMNhT5mSFwxYxrWbdu3QjC0ho6YsQItWjRophP0mjDIHJWGWB6XbT8+uuvatq0aapv374RFrJ48eKqRYsWupWVunEYuoui457Ib/RNYe2i9ST9VhKU0tLbQMSGOWRSMrkrAvFodOrZs6di7VcyIQeNTmy9OHLkSN1yXalSpf3/8T+r7LOYc//+/SMGXEDg8847Tw8MgJCuLLZFwxDpdkn33jxsJUFRiLe1llIUNwcr6qqsXbtWd+v06NFD1apVK4KU4BF9MPOD3b5wf3FZXV1ALcztDn7kResISgtivBLT3OecC4KFzcvLiyEm2NA/m40BE9nAXQiaDdQL+SYKwaWNFtPMbmsdNDo9ifweM2ZMDEFpcMolMS5udIu+KxhYZ0FxZWkM8gpWs0KFCta04Hrjnu41/ZXGvaWuyjjXXBIKZArsDh06OJls6whK4xB1TRqFOMzIEVp2c8l6enMjcyRdtSDedBZ0bbwn8sKAAQP00E8I60LLrnUExcU1BwrAerragldQhpT7sQhQQJEv8K44GN7nQqFlHUFjVSN3BAF3ERCCWq5brIRx971nmweIW64SX6MvBPUVzswHhptPI4lx+805V7qbMo94Zr8oBM0s3r5/LV6rtu8fkQCzhoAQNGvQ+/NhWrWxmiJuIiAEtVivdCvRByrurMVKLCLqQtAiAArz32YUDZPUvQ1EQtgway25uAlBk8MrVE/j2hoX1zQOcZZ+4VCpKa3ICEHTgi+7L9MhTyORiLsICEEt1q3pXrE4CRL1IhAQghYBUFj/xo2VBqKwase/eAlB/cMyoyGZAeIs6OU9pP6ZUTUE/jEhaOAQB/MBhvKZaWbeM8QVcQcBIag7upSUOIiAENRBpUqS3EFACOqOLiUlDiIgBHVQqZIkdxAQgrqjS0mJgwgIQR1UqiTJHQSEoO7oUlLiIAJCUAeVKklyB4H/AUXTueQ5No7MAAAAAElFTkSuQmCC[/img][br]Why is Clare's congruence statement incorrect?[br]
Write a correct congruence statement for the quadrilaterals.[br]
Triangle HEF is the image of triangle HGF after a reflection across line FH.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAO0AAACWCAYAAAAyqA+NAAAXR0lEQVR4Ae1dC5RN1Rv3yJJSQ0VFRWJKRpooNDQSg4SikBivWJVVQ5RHJRLyGCkkb0VUQoxBJs1ED89EeaWMPHqQEI3K4/uv3+6/b3funLlzH+ex9znft9Zd595zz9nn279v/85+ffvbhYiFEWAEtEKgkFbasrKMACNATFoPF4ItW7ZQgwYN8nxefPFFD6OiftaZtOrbyDINX331VYqJiSGQ1P+TmZlp2TM54egRYNJGj6G2KXTu3JkSExO11d+rijNpvWp5IqpRo4aoYT0MgZZZZ9JqabbolT527BgVKlSIFi9eHH1inIKtCDBpbYVbnYeh3wrSZmdnq6MUaxISAkzakGBy30UYeAJpAz9MYvVtzaRV30aWaNiqVSsxCIUa1/9jycM4UVMRYNKaCqc+iVWoUIEHofQxVy5NmbS54PDGDzSB0Szm+Vg97c2k1dNuUWmNEWOQFiPILPohwKTVz2ZRa4xBKDSPWfREgEmrp92i0ho+x/iw6IkAk1ZPu7HWHkaASeth43PW9USASaun3YJq/dxzz1H16tUpKSmJFi5cGPRa/lM/BJi0+tksqMbdu3fP4+W0evXqoPfwn3ohwKTVy15Btd23b18ewmJqp0WLFpSTkxP0Xv5THwSYtPrYKpemR48epVWrVtGIESOodevWdN111xkS1t+3uFq1aoQ1tBMmTKB169bR33//nStN/qEHAkxaDewEJ4hPPvmExowZQ+3ataMbbrghF0FjY2OpY8eO9Prrr4vQMf5Exffnn3+ehg8fTg8++GCee+Pj46lHjx40ZcoU2rx5M505c0YDRLytIpNWMfufOHGC1q5dSwgF88gjj9CNN96Yi6CVK1emDh060Pjx4+mLL76gc+fO5crB8ePHqVOnTlS4cGG67LLLBJFzXUBEhw4domXLltHLL79Mbdq0oUqVKvmeUaRIEbrjjjvoiSeeoJkzZ9I333xD58+fD0yCfzuIgKWknTVrFg0ZMiTPx8H8KvXokydPimbqxIkTqUuXLhQXF+cjD2pIkKl9+/Y0btw4+uyzz8KqBUHYQYMGhZzfgwcPUlpaGr300kuiuV2xYkWfLhdeeCHVq1ePevfuTXPnzqXt27eHnK6XLkR5R6C8UqVKCezwHZiZ7S5qKWlR8BDSBHGI/D9eMqTM659//kkbNmwQzVA0R9Es9W/GgiRt27alsWPH0po1a6Lub4ZLWqmn//HAgQO0dOlSGjp0KN1///25+s2XXHIJ3X333fTMM8/Qe++9R7t27fK/1VPfQcpbb71VBMlLSUkR0UDg343vVsTgsoy0cJNDofSiu9zp06dp06ZNonmJZiaam2h2SpJi0Aj9y9GjR1NWVhbherPFDNIa6bR//35asmSJaD1hTW758uV9+br88supSZMmhHliFNrvvvvOKAnXnUPFhI/ZNWp+QFlGWjQVUEjdLhiB/eqrr2jOnDnizZqQkEDFixf3FeRrrrlGNDdfeeUVsRQONa4dYhVpjXTHVNOHH34o1ue2bNmSrrrqKl/+8f2+++4TJEet/cMPPxgloe05jD2gnNsZ8cMyVrkxPCdGVr/++muaN28e9evXT/RfSpYs6Sug5cqVE81ITMPAoQF9VqfETtIa5RGFeNGiRTR48GBB2rJly/pwQksD01TAKT093dYCb6RrNOewWgpl3U6xjLRoLqCd7z8QhdpXF8Go7LZt2+jdd9+lgQMHUuPGjal06dK+gnf11VcTahWMwGZkZBBGfVUSp0lrhMXevXuFWyWmoJo1a0ZoTssuA6axMJ2Faa0VK1YQmuGqi+wCBka0RHABdHvwsaIGtoy0MEbgIBSaEqrKt99+S++//76oGe69917yrxmuvPJK4VWEkdWPPvrItr5LNFipSFqj/KC5/MEHH4h+MPrD/i/GqlWriukrlBs4kmCEWyUBOQObxpLI8mWEtctmiyWkNcqM2YpHk96OHTtEQcGoaOBgSpkyZah58+aihYA3PjyPdBRdSGuE7ffff08LFiwQU1aNGjWiSy+91Fcj33LLLdStWzd67bXX6OOPP6aff/7ZKAlbzsmIlkYPszKkjyWkxZsRe8SoIJiKQN9q2LBhwpEAfRD5FkTzDM00gI++1ZEjR1RQ2RQddCatEQAYiUZLqH///tSwYUPyH0uoVasWPfbYY4T5blQYhw8fNkrC9HMybI9RE1j+Z8WIsiWkleE5TUepgARhWIxiwmUPTgnwHpIERbMLza8XXnhBOBH8+uuvBaSm999uI62RNXbv3i3GHDBXjPnQEiVKCHsXK1aM6tatS7169aI33niDPv30U/rtt9+MkojqnGwKGzWBcQ7dQyvEEtLaEZ4TTShMIYwcOVL43aL/IwmKWh4DR5gvxJyik00oK4wWSppeIK0RDmhZzZ8/n55++mmqX7++b/rt4osvFsR+6qmnhIMLPMzMqAUxcgwPKLiVyhoXRwzCWjWqbDppAYQkj/8xmrcORh3hKztq1ChKTk4m9Gtk2vDMueeee8QIL5ok8KtlIeF3HI4bo5sx27lzp5img0vhnXfeSRdccIEoPyAb+sw4P23aNOHLHe4sAMq77NvKMokjynvgqLJZGFtCWvQrAj+hekb9+OOPtHz5cjH0D3/cmjVr+giKtyVc59CvQUQGuNmxGCPg1ZrWGI28ZzEYCYeYJ598kmrXru3zWMOsQdOmTalv377Co239+vV06tSpvAkYnEENG2o5N7g95FOmkzbkJxMJ0q1cuZJSU1PFiCDAk29B9E/QT0F/BSOJIDNL6AgwaUPHSl6Jab+33npL9IVvv/12X2UBV01MA6Iszp49mzZu3OhoUAHbSItmK+baMLL86KOPioECOXAAtz/0P/B2g/O57BtIMPkYPgJM2vAxM7oDSxOxRBGj07fddpuPyNdff72Yux8wYICoseHKaldQgbBJi2bvww8/LGpB+NMaCQZ+MIeGubSePXsS/HHlXBtG9vC7T58+YsDAbb6oRng4cY5Jax3qW7dupenTp4uyjQEn2ZetUqWKcGPFWMI777wjXF6Nggrgfsw1gwcYLD179mxYyoZFWiwtkwrKIyImIKoCQpjgbYQaEwUG/xctWlTUqFiihEzs2bMnLOX44sgRYNJGjl0kd6Ivi+gfCKyHSJiSHwhiAD9rTDXCJRaVnuSHvAYLKsKRsEiLUTb5oMAjIiWgT4qOPTr4mENjcQ4BJq1z2MsnY3km5om7du1KiM8VyBn/3+EEFgiLtKjS/R8kv2PRNotaCDBp1bKH1AatUckb/yNGqUOVsEgLx27/B+E7QpFglQuLWggwadWyh9QGI9CBHEITOhwJi7RIGB5IWPWCB8NVTMYSQjOARR0EmLTq2EJqAm8s8Abeehh9xneMAYVTyyKtsEkrFZAhUjBSjDksKIA+L4saCDBp1bADtMCSQvi9gyNTp071KRZpkISISet78v+/yEEqEPinn34K/Jt/24wAk9ZmwPN5HGZWUKsiaAJC45ohppEWykyaNEm8TbC6BisrWJxDgEnrHPbyyZMnTxZ8gOutmcs+TSUtlMWglNyiAk7YLM4gwKR1Bnf5VDgPoTmMaJxmi+mkhYLwE8bKGyiN0TIW+xFg0tqPOZ6IMR5EPkHZh8ORFWIJaaWijz/+uFAei+KtWIQsn8PHvAgwafNiYvUZdAnRNQT2Vk6DWkpagIQFAnjrYJE69p5hsQcBJq09OMunYFQY5Rzrda0OQGc5aZEpLGBH0Gr4ImNpE4v1CDBprcdYPgExsEFY+B3bIbaQFhlB/CZMJCNzHFHBetMyaa3HGCPCiH2NMo14zXaJbaSVGcLbCJnEXjZ//PGHPM1HkxFg0poMaEByiDEF90OEO0JL0k6xnbTIHNbhgriI9YQoACzmI8CkNR9TmSIWxWNVGxbFI8Cg3eIIaZFJxCJGwUL0Cqy1ZTEXASatuXjK1BCfDBUONvx2ShwjLTKMmDzYBhIgGMWOdQoUNzyXSWuuFRF18YEHHhBlFfs3OSmOkhYZR1wdRL8AcRHG5q+//nISD9c8m0lrnim//PJLsYgdrUIsT3VaHCetBACbW4G42OIB20myRIcAkzY6/OTdiM6ICKFxcXEUTnQJeb8VR2VIi8whMjxG4xAEDvu2sESOAJM2cuzknQi6hooEMx3Y+lQVUYq0AGXz5s1iSwWA5XTfQRUjRaIHkzYS1P69B+tcQVSUQeylq5ooR1oABNAeeughARr2Qzl//rxquCmvD5M2MhNhChJTkWgSqzqroSRpJdyyeYKwNtjGgSV0BJi0oWMlr5w7d66IeQanCbT4VBWlSQvQMBCA4HHYS9aqDY1UNU40ejFpw0Nv8ODBomWHGMQ5OTnh3Wzz1cqTFnjIIXf0MbBzHkvBCDBpC8YIVyDWGfYyRtnSZe23FqQFuFiPi3W5ABd7AbEER4BJGxwf/ItdAeLj40WZmjFjRsE3KHKFNqSVeMm4sXfddZcjfp9SD9WPTNrgFsIWHdg6tVKlStqt89aOtDAFFhxjbS7W6Kanpwe3jkf/ZdLmb/ihQ4eK2jUpKYl+//33/C9U9B8tSQsss7KyKDY2VoCP6BgsuRFg0ubGA7+wgx0c/dHFwp5Tuoq2pAXgiK/crFkzYQTEo2L5DwEm7X9Y4Bv2mZUbReu+G4bWpJVmkdstIALk/v375WlPH5m0/5l/wYIFwjUWoX0RPFx3cQVpYYSJEyeKGvfaa6+1NBKeLgZn0v5rKbjCojmMgOEIb+oGcQ1pYYxVq1b5NjYCib0sTFqi5ORkQdiePXu6qii4irSwTHZ2NjVq1EgYC81mr4qXSbtz506qU6eOKAPjxo1zXRFwHWmlheTmvU2bNqVffvlFnvbM0aukhatr6dKlxYZXK1ascKW9XUtaWCs1NVW8bTGB7rUNwbxIWhkwsF69eqLF5UrGRrM/rS6ApKWlUfny5QV5p0yZoovaUevpNdJ27dpV2BhLOd0urq5ppfF2795NiYmJwqh9+/aVp1199App9+zZQwkJCcK2I0eOdLVNZeY8QVqZ2W7dugnjtmjRQkv3NZmPUI5eIC1aUWXKlKErrrjCU8s2PUVaFHa8jTFvh4XOWPLnVnE7abENB+xYu3Zt2rVrl1vNaJgvz5EWKCxcuJDKli1LRYoUoVmzZhkCo/tJN5O2R48egrBOBgx3snx4krQAfNu2bWJbQrytBwwY4KQNLHm2G0mLOXgsyYTNvBzc3rOkBVMQGL1Tp06iELRu3ZpOnTplCYGcSNRtpMWcK5ZixsTEENbCelk8TVpp+CFDhgjiVq9eXemAXlLfUI5uIq3cmBwbXnEgeyIm7f8ZMG/ePOFJU7x4cWVDZ4ZCVnmNW0grPdvatm0rtpCR+fPykUnrZ/1NmzaJbUnQZ0J0Pp1Fd9IeOHCAGjZsKFpAAwcO1NkUpuvOpA2A9MSJE77ofO3ataN//vkn4Ao9fupM2oyMDOHFdtFFF9Hs2bP1ANxGLZm0+YAtA6WjH4WoB7qJrqSdMGGCqF0R5X/9+vW6wW6LvkzaIDDjLV+yZEnxQfQDnURH0vbq1UsQFvvAosXDYowAk9YYF9/Zzz//nGrUqCEKk04bgulEWkSUaNy4scC4X79+Puz5izECTFpjXHKdPXLkCGEeFwNUmNfVQXQhbWZmJlWoUIGKFStGXlqFFU0ZYtKGgd6zzz4riAt/V6wcUll0IO3kyZMFnlWrVvXceudoyg6TNkz0UBtgLhfREZYsWRLm3fZdrjppU1JSBGGx4dXhw4ftA8YFT2LSRmBENOluvvlmUehGjx4dQQrW36IqadHVQAggdDV69+5tPRAufAKTNkKjHjx4kLAuF4UP63RVExVJu3btWrF3TuHChQlTOyyRIcCkjQw3312oLUBc1eISqUbaadOmCZwqV64sQt36AOQvYSPApA0bsrw3IMYyag+s0VUlAqBKpEWIH7zYmjRpwjtA5C0+YZ9h0oYNmfENK1eupCpVqojCOX78eOOLbDyrAmmPHTtGzZs3F5jAcYLFHASYtObgKFLZu3evb5AFq1OcFKdJi1A+8iXmxoDhTtqWSWsB+tIdD/vHHDp0yIInFJykk6RFCB80h+E0sXTp0oKV5SvCQoBJGxZcoV8sF24j5vLq1atDv9GkK50ibf/+/QVhsYMhwpuymI8Ak9Z8TH0popZBbYNax+49Ue0m7cmTJ6lVq1Yir27b8MpnUEW+MGktNgQ2g0KtA+LauSGYnaTduHEj3XTTTSKPo0aNshhRTp5Ja0MZOHfuHKH2AXGTkpIIXkFWi12knTNnjghFW65cORGa1up8cfocI8rWMoBaCMStWLEiwTvISrGDtDJQAMKa6hgowEr8rUyba1or0TVIG4HSUSuBvNOnTze4wpxTVpL29OnT1KZNG5EHbHx19uxZc5TmVEJCgEkbEkzmXrR161aqX7++KPRWLfq2irRbtmyhuLg4ofvw4cPNBYZTCwkBJm1IMJl/EWoruT0jlqeZHV7FCtLOnz9fLFaHu6bXA4abXyJCT5FJGzpWllyJEDZoKsfGxpoayMxs0mIbDuhZt25dQqhZFucQYNI6h73vyajBsGUjSPH222/7zkfzxSzSnjlzhhBKFrp17NjRVVunRIOvk/cyaZ1E3+/ZmOusU6eOIMegQYP8/onsqxmkxYiwDGqHrVNY1ECASauGHYQWx48fF7UZajUEkkO/N1KJlrQIGVuiRAkRVgdzsSzqIMCkVccWPk1k/7FatWqE0dpIJBrSDhs2TNT4tWrVcvXG25HgqsI9TFoVrGCgA/q2pUqVEqO1kYzURkpabNSMmr59+/Z09OhRA834lNMIMGmdtkCQ5yNQes2aNQWJwu1Thkta+EjLZ8HTiUVdBJi06tpGaIbwotjmUdZ+8GMORcIh7eLFi33bn8ycOTOU5PkaBxFg0joIfjiPxogyiBsfH0/bt28v8NZQSTty5EiRLkaJ16xZU2C6fIHzCDBpnbdByBrMmDGDsP0jPosWLQp6Xyik7dy5syAs/IidirARNBP8pyECTFpDWNQ9mZWVRdgGErXuiBEj8lU0GGkRUQJbmyANbHXCohcCTFq97CW0RaB0bAcJ0iUnJxvmID/SpqWlUUxMjNjaZOrUqYb38km1EWDSqm2foNphhRCIi1ozMB6TEWnHjBkjrsf8rxNxq4Jmhv8MGQEmbchQqXnhm2++KeZyUXsuW7bMp2Qgabt37y4I27JlS9q3b5/vOv6iHwJMWv1slkfjjIwMwnaRqHXHjh1L69atEy6I2Ohqx44dlJCQIP7r06dPnnv5hH4IMGn1s5mhxgiUjnW5IK7/p2jRoiKG06RJkwzv45P6IcCk1c9mQTXGdJA/afG9Q4cOQe/hP/VCgEmrl72Caou51kDC4jdGmlncgwCT1j22FDnByHAgcVNTU12WS29nh0nrMvunp6eLNbCSuNj4msVdCDBp3WVPkZucnBxavnw5bdiwwYW54ywxabkMMAKaIcCk1cxgrC4jwKRVvAwg3EyDBg0oOzs7j6bYBxYrdVi8hQCTVnF7yw2ajdRMTExk0hoB4/JzTFrFDZySkkIgp5HA3xibV7N4CwEmreL2RkQJEDdQ0FzGtE5mZmbgX/zb5QgwaRU3MIiJJnKgIK4T/mPxHgJsdYVtjloUxOzSpQshGqP/B4NTqIVZvIcAk1Zhm6O/in4rgpcHfipUqGDYbFY4O6yaSQgwaU0C0opkMJ2T3yBUfs1mK/TgNNVCgEmrlj1yaYPaFDVsoGDuFqSNdMuQwPT4t14IMGkVtdexY8cEMTHgFCjB5m4Dr+Xf7kOASauoTeUgFMgbKMGazYHX8m/3IcCkVdSmaBajeWwkGDU2ajYbXcvn3IcAk1ZRm8J5Ir8+K2phI19kRbPCapmMAJPWZEA5OUbAagSYtFYjzOkzAiYjwKQ1GVBOjhGwGgEmrdUIc/qMgMkIMGlNBpSTYwSsRoBJazXCnD4jYDIC/wPcqQcF5IX7tQAAAABJRU5ErkJggg==[/img][br]Select [b]all[/b] statements that must be true.
When rectangle ABCD is reflected across line EF, the image is BADC.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUwAAACOCAYAAABaOTFUAAAMYUlEQVR4Ae3czWsTXRTH8biQKkVasIIotEXBldD+B+3WVXxZKUpE1IUUWjeiWGkWitBNuxPcVNFNRYlvCL5AQtV1QQRBhSLiRilddSEI9+EMz+SkmZM0qWnM3PsdGDyZTJu5nzv3l3mrGceEAAIIINCQQKahtVgJAQQQQMB5GZhzc3NOZiYEEGifQLFYdPl8vjzPzs66paWl9m1AGz7Ju8CUDspkMtHcBj8+AgEE/hcYGRlxMk9NTblsNusGBgZcb2+vVwcv3gWmdNTQ0BCByTBGoM0CPT09bmZmpvypKysrUXBKaErtw+RVYMopgRxdxkeZ8poJAQQ2X2BxcTEae/Jv5SRBKWPSl0tkXgWmnA7kcrmov6STCMzKXZcagc0TkECUMWdNcuQpp+k+THYLU9iyQqHgpGPiQ385Lfelk1LYHWxyYALj4+PR9Uur2XIt05ex6E1gVndKfPHZ6kCWIYBAawVkvEloWpMceVZe27TWScsyLwJTOkM6pXqWTmRCAIHNF5CxJ2d51ZMsk/d8ebwo9YEpp+ByF06+3eSaZTzLtUwCs3r35TUCrReQMVcrFOXSmE/jMPWBKddG5HS8eqp3Ebp6XV4jgMDGBeQMT+4fVE5yIHP69OloefWd88r10lanOjDlML/Wg7Hxt17aOoTtRSBtAnI2Nzw87Eqlknv8+LGbmJhwg4OD0YGMT2Ep/ZLqwJRvNnlQ3ZokTOVUwLcOs9rKMgT+pUB8h1zGm8wyJuUML35i5V9uW6s/O9WB2WoMfh8CCCBQT4DArKfDewgggECFQLCB+e7dO/f169cKCkoEELAE/vz54xYWFrx5NMhqY6PLggvM169fu71795af2Tx79myjVqyHQHACT58+dX19feXxMjY2FpxBZYODC0y5m1f9gLv8v31fvnxhxoB9oGof6O/vT4yX58+fV2ZIUHVQgfnr169E51eHJ6+TfzGFCSaV+8Dk5GRQIVnZ2KACUxq+b9++RGhevHjRvXz5khkD9oGqfUCec64MS6nn5+crMySoOrjAvH///pod4NChQ0F1OI1FoBmB27dvrxkvR48ebebHvVs3uMCUHvz27Zvr6upy586d865DaRACrRb4/PlzFJpyJhb6FGRgSqd3d3e76enp0Puf9iOwroA8ViSn4rdu3Vp3Xd9XIDB972Hah8BfChCYCkhgqgUVAggYAgSmohCYakGFAAKGAIGpKASmWlAhgIAhQGAqCoGpFlQIIGAIEJiKQmCqBRUCCBgCBKaiEJhqQYUAAoYAgakoBKZaUCGAgCFAYCoKgakWVAggYAgQmIpCYKoFFQIIGAIEpqIQmGpBhQAChgCBqSgEplpQIYCAIUBgKgqBqRZUCCBgCBCYikJgqgUVAggYAgSmohCYakGFAAKGAIGpKASmWlAhgIAhQGAqCoGpFlQIIGAIEJiKQmCqBRUCCBgCBKaiEJhqQYUAAoYAgakoBKZaUCGAgCFAYCoKgakWVAggYAgQmIpCYKoFFQIIGAIEpqIQmGpBhQAChgCBqSgEplpQIYCAIUBgKgqBqRZUCCBgCBCYikJgqgUVAggYAgSmohCYakGFAAKGAIGpKASmWlAhgIAhQGAqCoGpFlQIIGAIEJiKQmCqRaIqFosun88n5qWlpcS6LEDAV4FGAzOE8UJg1tnLs9msGxkZcVNTU2vmlZWVOj/FWwj4JdBoYMpYscaLTxoEZp3e7OnpcTMzM3XW4C0E/BdoNDAzmYybm5vzGoTArNG9ctotO4CcZjAhELJAI4G5uLgYjRf51+eJwKzRu4VCIdoBarzNYgSCEWgkMOXIUg4wfJ/8b2GNHuzu7nbT09M13nXRNcve3l43OjpanuWaJhMCoQk0Epjj4+NueHjYlUql8uzj0SaBWWPvty5g+359pgYFiwMXaCQwh4aGoiNMOcqMZx8PMAjMGoNBOp2ArIHD4qAEGglMGS9yGcv3icA0ejiUC9hG01mEQEJgvcCUG6MSmCE8n0xgJnYPFx1Zyg7AhAACzq0XmPLonTyCF8IUbCrUu+kjF7AHBwcTf+HDA+shDAnaWC2wXmDmcjnn4/XKagd5TWAaKhKY8U2fyn+NVVmEgPcCjQRmKNf7CUzvd3caiMDfCawXmH/329P10wRmuvqLrUWg7QIEppIHGZirq6tu27ZtbmJiQiWoEEDAFFheXo7ugl+7ds18P6SFwQXms2fPojt6chdc5hMnToTU37QVgaYE5ufn3fbt28sPo585c6apn/dt5aYCU55PTPu8f//+cufHoXn9+vXUtyvt/cL2d+bY2r17d2K8yGNEae+vjQZ5U4H59u3bBF4cOvyrfxKGBRbsA527Dxw5cmSjedncY0Xv3793aZ/7+/sToT85OZn6dqW9X9j+zhxbu3btSoyXGzdupH68bDQxmzrC3OiHdNLPPXr0KLrhEx8BHDt2rJM2j21BoKME7t2757Zs2VIOzZMnT3bU9rV7Y4ILTAGWu35yl3xsbKzd3nweAqkT+PHjRxSYly9fTt22t3qDgwxMQaz3p5GtRub3IZBmAZ7D1N4jMNWCCgEEDAECU1EITLWgQgABQ4DAVBQCUy2oEEDAECAwFYXAVAsqBBAwBAhMRSEw1YIKAQQMAQJTUQhMtaBCAAFDgMBUFAJTLagQQMAQIDAVhcBUCyoEEDAECExFITDVggoBBAwBAlNRCEy1oEIAAUOAwFQUAlMtqBBAwBAgMBWFwFQLKgQQMAQITEUhMNWCCgEEDAECU1EITLWgQgABQ4DAVBQCUy2oEEDAECAwFYXAVAsqBBAwBAhMRSEw1YIKAQQMAQJTUQhMtaBCAAFDgMBUFAJTLagQQMAQIDAVhcBUCyoEEDAECExFITDVggoBBAwBAlNRCEy1oEIAAUOAwFQUAlMtqBBAwBAgMBWFwFQLKgQQMAQITEUhMNWCCgEEDAECU1EITLWgQgABQ4DAVBQCUy2oEEDAECAwFYXAVAsqBBAwBAhMRSEw1YIKAQQMAQJTUQhMtaBCAAFDgMBUFAJTLagQQMAQIDAVhcBUCyoEEDAECExFITDVggoBBAwBAlNRCEy1oEIAAUOAwFQUAlMtqBBAwBAgMBWFwFQLKgQQMAQITEUhMNWCCgEEDAECU1EITLWgQgABQ4DAVBQCUy2oEEDAECAwFYXAVAsqBBAwBAhMRSEw1YIKAQQMAQJTUQhMtaBCAAFDgMBUFAJTLagQQMAQIDAVJcjA/Pnzp+vq6nIXLlxQCSoEEDAFvn//7jKZjLt06ZL5fkgLgwvMBw8euK1bt0Y7gOwEhw8fDqm/aSsCTQncvXu3PFZkvBw/frypn/dt5eAC88CBA2t2ANkJrly54hYWFpgxYB+o2gd27tyZGC8PHz70LQcbbk9Qgbm8vJzofAlMZgzYBxrfB65evdpwwPi2YlCBKZ138ODBREDevHnTffjwgRkD9oGqfWDPnj2J8fLkyRPfcrDh9gQXmC9evHB9fX3lneDUqVMNY7EiAqEJyOn3jh07yuPl/PnzoRGsaW9wgSmt//37t3vz5o37+PHjGgxeIIBAUmB1ddW9evXKffr0KflmYEuCDMzA+pjmIoBAiwQIzBZB8msQQMB/AW8Cc2Zmxo2OjpZneb7yzp07/vcgLUSgwwSKxaLL5/PRWJRxODs765aWljpsKze2Od4E5sjIiJN5amoqmnO5XHShWoKUCQEENl9gZWUl+kMQeURLxl88FoeGhpyEqA+TN4EpnTQ3N7emT7LZbBSiaxbyAgEENkVADlh6enrc4uLipvz+TvilXgSmdJAEZnVHEZidsIuxDSEIyMGKNQZ9a7sXgSmdJd9slZOciksH+nIqUNk2agQ6TUBOu+U03PfJi8CUjurt7Y0uMg8PD0dBKacH1Uecvncm7UPgXwjIDR05OCkUCv/i49v6mV4EZvztJkeTMsvRpRxxVl/TbKssH4ZAIAIy5iQw5aaP75MXgWl9u0loylEnEwIIbK5AfPlrcz+lM3576gOz1rdbfBG6M5jZCgT8FYjHoC/PWtbrqdQHpny7DQwMJNoYP5eZeIMFCCDQUoH4GqY8d+n7lPrAlEeHBgcHo78skL8ukFleS4hy08f33Zf2dYqAhKVcGpPxVyqVoln+0k6OPn2aUh+Ycoc8PpqUf6XjuNnj0y5KW9IiIGd7cgNWglNmqX27c576wEzLzsR2IoBA+gUIzPT3IS1AAIE2CRCYbYLmYxBAIP0C/wGOXWt8SNsalgAAAABJRU5ErkJggg==[/img][br]How do you know that segment AD is congruent to segment BC?
This design began from the construction of a regular hexagon.
Describe a rigid motion that will take the figure onto itself.