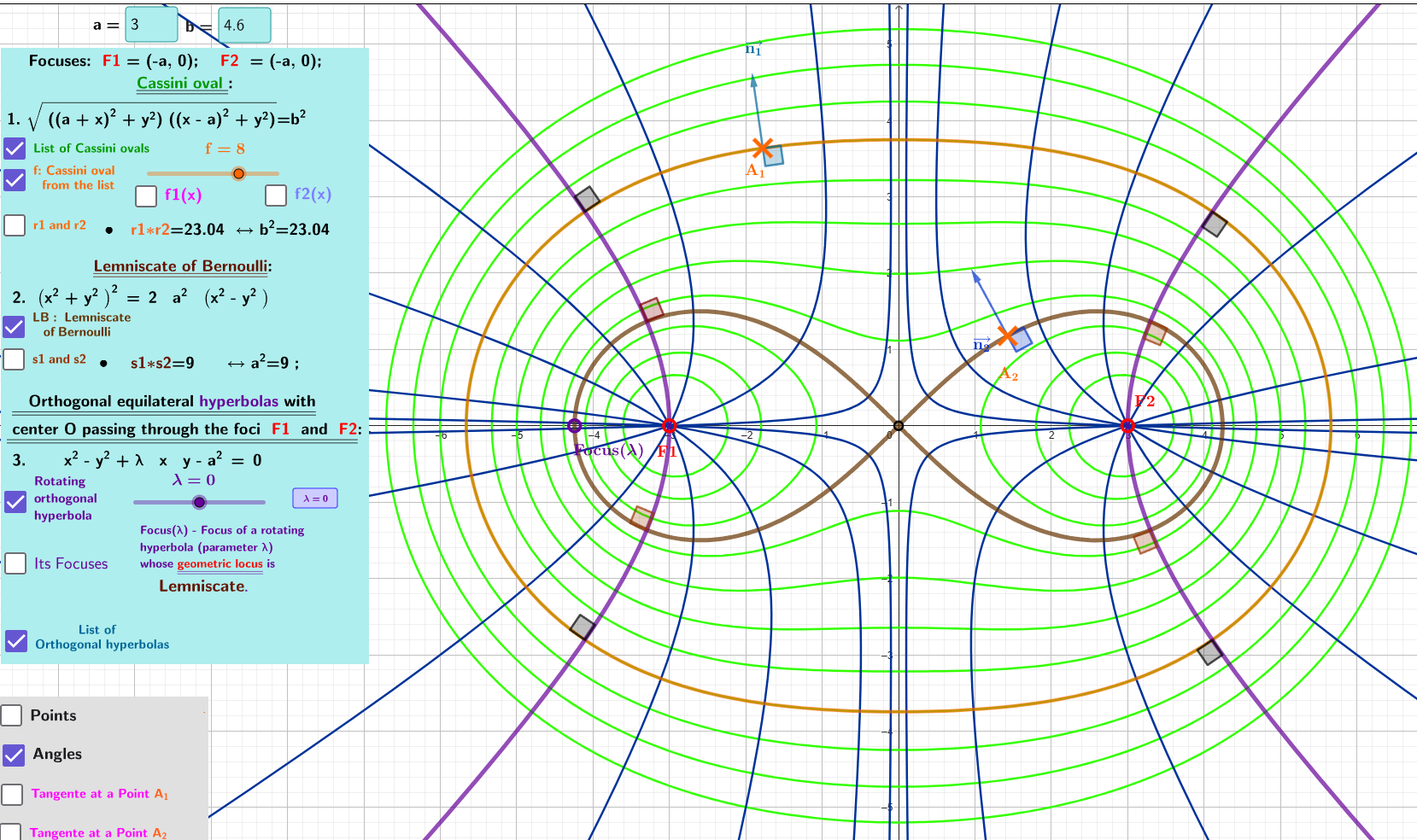
Cassini ovals and their orthogonal trajectories (hyperbolas)
[size=85] The applet visualises the geometric properties of [url=https://en.wikipedia.org/wiki/Cassini_oval]Cassini lines[/url] and their associated [url=https://en.wikipedia.org/wiki/Lemniscate_of_Bernoulli]Bernoulli lemniscate[/url] - fourth-order curves that represent the locus of points such that the product of the distances of these lines to their two foci is constant.[br][br] 1. The [b][color=#980000]Lemniscate of Bernoulli[/color][/b] is from the [b]family of[/b] [b][color=#38761d]Cassini ovals[/color][/b] where b=a.[br] 2. For an [i]arbitrary[/i] point [b][color=#ff7700]A1[/color][/b] of the [b][color=#38761d]Cassini oval[/color][/b] with [b][color=#ff0000]foci[/color][/b]: [b][color=#ff0000]F1[/color][/b] and[b][color=#ff0000] F2[/color][/b] the [color=#1e84cc][b]normal[/b][/color] is the[color=#1e84cc] [b][url=https://en.wikipedia.org/wiki/Symmedian]symmedian[/url][/b][/color] of the triangle [b]△[color=#ff0000]F1[/color][color=#ff7700]A[sub]1[/sub][/color][color=#ff0000]F2[/color][/b].[br] For an [i]arbitrary[/i] point [b][color=#ff7700]A2[/color][/b] of the [b][color=#980000]lemniscate of Bernoulli[/color][/b] with [b][color=#ff0000]foci:[/color][/b] [b][color=#ff0000]F1[/color][/b] and [b][color=#ff0000]F2[/color][/b] the [b][color=#1e84cc]normal[/color][/b] is the [b][color=#1e84cc]symmedian[/color][/b] of the triangle [b]△[color=#ff0000]F1[/color][color=#ff7700]A[sub]2[/sub][/color][color=#ff0000]F2[/color][/b].[br] 3. The [color=#333333]rectangular (or equilateral)[/color][b] [url=https://en.wikipedia.org/wiki/Conic_section#Standard_forms_in_Cartesian_coordinates]hyperbolas[/url]:[/b] [b]x² - y² + λ x y - a² =0 [i]o[url=https://en.wikipedia.org/wiki/Cassini_oval#Cassini_ovals_and_orthogonal_trajectories]rthogonally[/url][/i][/b] intersect both the [b]family of[/b] [b][color=#38761d]Cassini ovals[/color][/b] and the [b][color=#980000]Bernoulli lemniscate[/color][/b] with the same[b] [color=#ff0000]foci[/color]: [color=#ff0000]F1[/color][/b] and [b][color=#ff0000]F2[/color][/b]. Moreover, the [b]locus[/b] of the [b][color=#9900ff]foc[/color][/b]i of these [b][color=#9900ff]hyperbolas[/color][/b] is the [b][color=#980000]lemniscate of Bernoulli.[/color][/b][/size]
Constructions
