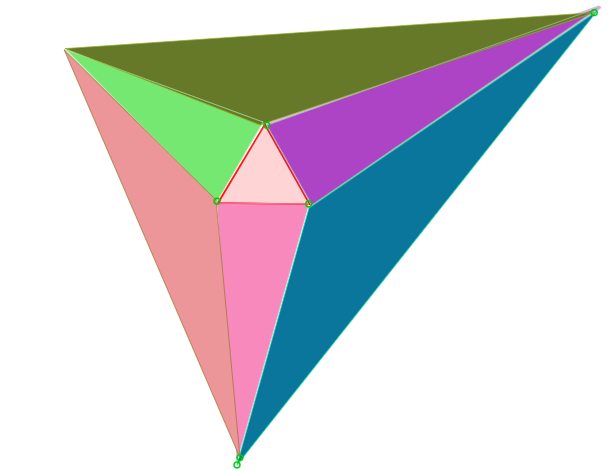
[br][justify]Frank Morley fue un matemático inglés que en 1887 se trasladó a EEUU para trabajar en el Haverford College (Pensilvania). En 1889 pasó a la Universidad Johns Hopkins, en Baltimore, institución en la cual permaneció durante 27 años hasta su retiro de la actividad docente e investigativa formal.[br][br]En 1900 escribió el artículo “[i]On the Metrics Geometry of the Plane n-lines[/i]”, publicado en la revista “American Mathematical Society Translations” y diversos autores reconocen que en el contenido de dicho documento[br]se encuentra, de manera no explícita, el resultado conocido como “[i]El teorema de Morley”. [br][br][/i]En su forma más simple esta proposición establece que: [br][br][i]“Los puntos de intersección de las trisectrices interiores adyacentes de los ángulos de cualquier triángulo determinan un triángulo equilátero.”[/i][br][br]A partir de ese momento y durante más de 125 años se han publicado, y se siguen publicando, diferentes demostraciones de este resultado y artículos relacionados con el mismo; en particular en el año 2014, el profesor John Conway publicó en la revista The Mathematical Intelligencer, vol. 36, n. 3 el pequeño artículo [i]On Morley’s Trisector Theorem[/i], el cual contiene, por el momento, la demostración que se considera más sencilla del teorema de Morley.[br][br]A grandes rasgos esta demostración consta de dos pasos básicos, a saber,[br]a.      A partir de tres ángulos dados, cuya suma debe ser 60°, construir siete triángulos con características especiales, uno de los cuales debe ser equilátero.[br]b.     Demostrar que estos triángulos se “acoplan” en un nuevo triángulo, semejante a uno dado cuyos ángulos son tres veces los ángulos conocidos.[br]La siguiente gráfica ilustra el “encaje” de estos triángulos.[/justify]

El siguiente recurso GeoGebra permite visualizar un rompecabezas que se ha elaborado a partir de esta demostración y la tarea, para Ud. amable lector, consiste en armar el triángulo a partir de estas 7 piezas para lo cual se presentan algunas orientaciones. [br][br]Cuando se activa la casilla [b][i]Presentación[/i][/b] se muestran un botón y tres casillas de control. [br][br][justify]·        Al dar clic sobre, el botón “Nuevos ángulos”, se modifican los valores de los ángulos y consecuentemente el tamaño de los triángulos, así como su color. [br]·        Al activar la casilla “Teorema de Morley”, se muestra el enunciado de esta proposición.[br]·        Al activar la casilla “Instrucciones”, se muestra las indicaciones que permiten trasladar y rotar los triángulos.[br]·        Al activar la casilla “Puntos” se muestran los vértices del triángulo que debe acoplarse. [br]La siguiente gráfica muestra los 7 triángulos “desacoplados”.[/justify]