Persamaan Garis

Ummi Mamlaul Khoiriyah, 24/09/2025

Buku ini merupakan salah satu produk pembelajaran yang disusun sebagai implementasi dari kegiatan SEAQiM – In Country Course on Integrating ICT in Mathematics Education for Junior High School Mathematics Teachers, yang diselenggarakan bekerja sama dengan Musyawarah Guru Mata Pelajaran (MGMP) Matematika SMP Kabupaten Tanah Laut. Kegiatan ini bertujuan untuk meningkatkan kompetensi guru dalam mengintegrasikan teknologi informasi dan komunikasi (ICT) ke dalam pembelajaran matematika, sehingga proses belajar menjadi lebih inovatif, interaktif, dan kontekstual. Materi Persamaan Garis Lurus dipilih sebagai fokus penyusunan buku ini karena memiliki peran fundamental dalam kurikulum matematika SMP sekaligus menyediakan ruang luas untuk integrasi ICT, khususnya melalui pemanfaatan perangkat lunak GeoGebra. Dengan menggunakan GeoGebra, peserta didik dapat secara langsung memvisualisasikan konsep-konsep penting seperti gradien, bentuk-bentuk persamaan garis, dan hubungan antar garis di bidang koordinat. Interaktivitas ini memungkinkan pembelajaran menjadi lebih bermakna karena siswa tidak hanya menerima penjelasan abstrak, tetapi juga dapat mengeksplorasi, memanipulasi, dan menemukan pola secara mandiri. Buku ini disusun secara sistematis dengan cakupan materi meliputi: 1. Konsep dasar bidang koordinat dan garis lurus, 2. Gradien garis lurus serta interpretasinya, 3. Menentukan persamaan garis melalui titik tertentu, dua titik, serta garis sejajar dan tegak lurus, 4. Hubungan antar garis (sejajar, tegak lurus, dan berpotongan), dan 5. Aplikasi persamaan garis dalam kehidupan sehari-hari. Setiap bagian diperkaya dengan ilustrasi visual menggunakan GeoGebra, yang tidak hanya memperjelas konsep, tetapi juga melatih keterampilan peserta didik dalam memanfaatkan teknologi untuk memahami matematika. Buku ini juga dilengkapi dengan contoh soal, aktivitas eksplorasi berbasis ICT, serta latihan kontekstual yang menuntun siswa pada keterampilan berpikir kritis, kreatif, dan kolaboratif. Melalui buku ini, diharapkan peserta didik: - Memahami konsep persamaan garis lurus secara mendalam, - Terampil menggunakan GeoGebra untuk memvisualisasikan dan menyelesaikan permasalahan, - Menyadari relevansi matematika dalam kehidupan nyata, dan - Mengembangkan kompetensi abad 21 yang meliputi literasi digital, komunikasi, kolaborasi, serta kemampuan berpikir tingkat tinggi (HOTS). Dengan hadirnya buku ini, penulis berharap dapat memberikan kontribusi nyata bagi peningkatan kualitas pembelajaran matematika di SMP, khususnya di Kabupaten Tanah Laut, serta menjadi contoh praktik baik dalam mengintegrasikan ICT ke dalam kelas matematika. Semoga karya ini dapat menjadi inspirasi dan acuan bagi guru maupun peserta didik dalam mewujudkan pembelajaran matematika yang lebih inovatif, interaktif, dan bermakna.

Índice

  1. Presentasi Online
    1. Presentasi Materi Persamaan Garis
  2. Bab 1. Konsep Garis Lurus dalam Koordinat Kartesius
    1. Konsep Persamaan Garis Lurus
    2. Koordinat Kartesius
    3. Mengenal Persamaan Garis
  3. Bab 2. Gradien Garis Lurus
    1. Pengertian Gradien
    2. GRADIEN (KEMIRINGAN GARIS)
    3. Penjelasan - Gradien Garis
  4. Bab 3. Persamaan Garis Lurus
    1. LKPD PERSAMAAN GARIS LURUS
    2. Penjelasan Online
  5. Bab 4. Hubungan Dua Garis Lurus
    1. Hubungan antara Titik, Garis, dan Bidang pada Bangun Datar dan Ruang
    2. HUBUNGAN DUA GARIS
  6. Bab 6. Aplikasi Persamaan Garis Lurus
    1. APLIKASI PERSAMAAN GARIS LURUS

1.

Presentasi Online

  • 1. Presentasi Materi Persamaan Garis

1.1.

Presentasi Materi Persamaan Garis

– Ummi Mamlaul Khoiriyah

2.

Bab 1. Konsep Garis Lurus dalam Koordinat Kartesius

  • 1. Konsep Persamaan Garis Lurus
  • 2. Koordinat Kartesius
  • 3. Mengenal Persamaan Garis

2.1.

Konsep Persamaan Garis Lurus

pengertian Persamaan Garis Lurus
Persamaan garis lurus adalah persamaan yang jika digambarkan ke dalam bidang koordinat kartesius [br]akan membentuk sebuah garis lurus.[br][br]Jika dilihat pada grafik berikut, persamaan garis lurus memiliki perbandingan yang sama. Artinya antara selisih koordinat y dan selisih koordinat x bernilai serupa. Maka, persamaan garis lurus adalah perbandingan selisih koordinat y dan selisih koordinat x.[br]
Bentuk Umum Persamaan Garis lurus
Terdapat dua bentuk umum persamaan garis lurus yang harus [br]kita kenali. [br]1. Bentuk Implisit[br] [math]ax+bx+c=o[/math][br][br] Keterangan :[br] [math]a,b[/math] dan [math]c[/math] merupakan bilangan - bilangan nyata/Real[br] [math]x[/math] dan [math]y[/math] adalah variabel - variabel [br] [math]c[/math] adalah konstanta[br][br]2. Bentuk Eksplisit[br] [math]y=mx+c[/math][br][br] Keterangan :[br] [math]x[/math] dan [math]y[/math] adalah variabel [br] [math]m[/math] adalah gradien/ kemiringan garis [br] [math]c[/math] disebut konstanta
Untuk memahami lebih lanjut mengenai Persamaan Garis lurus perhatikan video berikut
pemahaman persamaan garis
1. Gambarlah grafik persamaan y = x + 2, y = 2x + 2 dan y = 2x − 3 pada bidang koordinat yang sama. Apa dampak perubahan grafik dari 1x menjadi 2x dan menjadi 4x? Jelaskan.[br][br]2. Gambarlah grafik persamaan y = 2x + 2, y = x + 5 dan y = 2x − 3 pada bidang koordinat yang sama. Apa dampak perubahan grafik dari +2, +5 dan −3? Jelaskan.[br][br]3. Gambarlah grafik persamaan y = 2x + 4, y = 2x − 8, y = 6, dan y = 2 pada bidang koordinat yang sama. Berbentuk apakah perpotongan keempat grafik persamaan tersebut?[br][br](masukan nilai persamaan pada geogebra berikut dan amatilah gambar hasil)
begitulah cara mengetahui persamaan garis dan bagaimana mengetahui konsep persamaan garis lurus.
– Syafiq Rofiqi

2.2.

–

2.3.

–

3.

Bab 2. Gradien Garis Lurus

  • 1. Pengertian Gradien
  • 2. GRADIEN (KEMIRINGAN GARIS)
  • 3. Penjelasan - Gradien Garis

3.1.

Pengertian Gradien

Pengertian Gradien
Definisi dari gradien adalah “Nilai kemiringan / kecondongan suatu garis yang membandingkan antara komponen Y (ordinat) dengan komponen X (absis).” Gradien akan menentukan seberapa jauh kemiringan yang terjadi pada suatu garis dalam koordinat Cartesius. Kemiringan atau gradien bisa miring ke kanan, ke kiri, curam, ataupun landai. Nilai dari gradien tergantung dari nilai komponen X dan komponen Y-nya.
Sifat-sifat Gradien
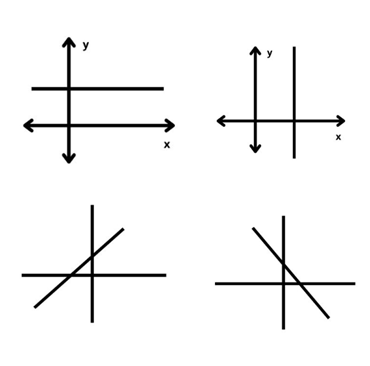
[size=100]1. Apabila suatu garis sejajar dengan sumbu x, maka nilai gradiennya adalah nol (0).[br]2. Apabila suatu garis sejajar dengan sumbu y, maka garis tersebut tidak memiliki gradien.[br]3. Apabila suatu garis miring ke kanan, maka gradiennya bernilai positif.[br]4. Apabila suatu garis miring ke kiri, maka gradiennya bernilai negatif.[/size]
– intan

3.2.

–

3.3.

–

4.

Bab 3. Persamaan Garis Lurus

  • 1. LKPD PERSAMAAN GARIS LURUS
  • 2. Penjelasan Online

4.1.

LKPD PERSAMAAN GARIS LURUS

TUJUAN PEMBELAJARAN :
a. Siswa mampu memahami konsep persamaan garis lurus dan bentuk-bentuk persamaan garis lurus.[br]b. Siswa mampu menentukan persamaan garis lurus dan gradiennya.[br]c. Siswa mampu menyimpulkan mengenai persamaan garis lurus dan hubungannya    [br]   dengan gradien.
PETUNJUK PENGGUNAAN :
1. Geserlah slider a b dan c1 untuk mengamati perubahan yang terjadi pada grafik persamaan pada fungsi ax+by=c1.[br]2. Geserlah slider m dan c untuk mengamati perubahan yang terjadi pada grafik persamaan pada fungsi y=mx+c.[br]3. Isilah titik titik pada input box untuk membuat 2 buah titik, centang grafik untuk menampilkan grafik persamaan garis lurus.
PETUNJUK PENGGUNAAN LKPD
Isilah kolom identitas yang disediakan, kemudian tulislah jawaban dari soal-soal yang disajikan pada kolom yang tersedia![br][br]Nama :[br]Kelas : [br]No Urut :
Perhatikanlah grafik persamaan garis lurus bentuk umum ax+by=c1, perubahan apa yang terjadi pada grafik saat : [br]a. a>0[br]b. a=0[br]c. a<0[br][br]
Perhatikanlah grafik persamaan garis lurus bentuk umum ax+by=c1, perubahan apa yang terjadi pada grafik saat : [br]a. b>0[br]b. b=0[br]c. b<0[br][br]
Perubahan apa yang terjadi pada grafik persamaan garis lurus bentuk umum ax+by=c1 jika nilai c :[br]a. c<0[br]b. c=0[br]d. c>0
Perubahan apa yang terjadi pada grafik persamaan garis lurus bentuk umum y=mx +c saat :[br]a. m>0[br]b. m=0[br]c. m<0
Perubahan apa yang terjadi pada grafik persamaan garis lurus bentuk umum y=mx +c saat :[br]a. c > 0[br]b. c = 0[br]c. c < 0
Tentukan persamaan garis yang melalui titik (6,8) dan titik (7,2)!
Tentukan nilai gradien garis yang melalui titik (4,5) dan (4,7)!
Tentukan persamaan garis yang melalui titik (0,7) dan gradien -1!
Dari hasil pengamatanmu apa yang dapat kamu simpulkan tentang gradien?
Dari hasil pengamatanmu apa yang dapat kamu simpulkan tentang pengaruh nilai gradien terhadap grafik persamaan garis lurus?
– murni

4.2.

–

5.

Bab 4. Hubungan Dua Garis Lurus

  • 1. Hubungan antara Titik, Garis, dan Bidang pada Bangun Datar dan Ruang
  • 2. HUBUNGAN DUA GARIS

5.1.

Hubungan antara Titik, Garis, dan Bidang pada Bangun Datar dan Ruang

Hubungan antara Titik, Garis, dan Bidang pada Bangun Datar dan Ruang
[list][b]Capaian Pembelajaran[br][/b]Peserta didik mampu memahami dan menjelaskan hubungan antara titik, garis, dan bidang dalam bangun datar dan bangun ruang, serta menerapkannya dalam menyelesaikan permasalahan kontekstual secara logis dan sistematis[justify][/justify][b]Indikator Pencapaian Kompetensi:[/b][/list][list=1][*]Mengidentifikasi hubungan posisi antara titik, garis, dan bidang[/*][*]Menentukan posisi relatif antara dua garis atau garis dan bidang[/*][*]Menggunakan model konkret atau digital (GeoGebra) untuk mensimulasikan hubungan titik, garis, dan bidang[/*][/list]
Materi
[b]Definisi Titik, Garis, dan Bidang[br][/b][b]1. Titik[br][/b]Titik adalah objek geometri paling dasar yang tidak memiliki panjang, lebar, atau tinggi. Titik hanya memiliki posisi atau lokasi dalam ruang[br]contoh: Titik A pada bidang atau ruang ditulis: A(x, y) atau A(x, y, z)[b][br]2. Garis [br][/b]Garis adalah kumpulan tak hingga dari titik-titik yang berjejer lurus tanpa ujung di kedua arah. Garis memiliki panjang, tetapi tidak memiliki lebar dan tinggi[br]jenis: garis lurus, sinar (ray): hanya memiliki satu ujung, segmen garis (line segment): garis dengan dua ujung tetap[b][br]3. Bidang[br][/b]Bidang adalah permukaan datar tak berhingga yang terdiri dari kumpulan titik dan garis yang membentang ke segala arah. Bidang memiliki panjang dan lebar, tetapi tidak memiliki ketebalan, bidang dapat dinamai menggunakan tiga titik yang tidak segaris, misalnya bidang ABC, atau satu huruf Yunani kecil, misalnya bidang α.[b][br][/b][b][br][/b][b]Hubungan antara Titik, Garis, dan Bidang[br]1. Hubungan Titik dan Garis[/b][br][list][*]Titik dapat terletak pada garis[/*][*]Titik diluar garis[/*][*]Titik tidak sejajar dengan garis[/*][/list][b]2. Hubungan Titik dan Bidang[br][/b][list][*]Titik dapat berada didalam bidang[/*][*]Titik diatas bidang atau diluar bidang[b][br][/b][/*][/list][b]3. Hubungan Garis dan Bidang[br][/b][list][*]Garis terletak pada bidang (seluruh titik garis ada di bidang)[/*][*]Garis menembus bidang (memotong bidang di satu titik)[/*][*]Garis sejajar bidang (tidak berpotongan sama sekali)[/*][/list][b]4. Hubungan Dua Garis[br][/b][list][*][/*][*]Sejajar: tidak berpotongan dan berada dibidang yang sama[/*][*]Berpotongan: bertemu di satu titik dan dibidang yang sama[/*][*]Bersilangan: tidak sejajar, tidak berpotongan, dan tidak sebidang[/*][b][br][/b][/list]
Soal 1
Diketahuai titik A terletak pada garis [math]\alpha[/math], maka dapat ditulis....
Soal 2
terdapat 4 titik yang saling berhubungan satu sama lain, tentukan jumlah garis yang terbentuk dari keempat titik tersebut....
Soal 3
Titik D(2, 3, 0), A(1, 1, 0), B(4, 2, 0), dan C(3, 5, 0). Ketiga titik A, B, C membentuk bidang α. Posisi titik D terhadap bidang α adalah...
Soal 4
Garis m melalui titik A(0, 0, 0) dan B(1, 1, 1). Garis n melalui titik C(0, 1, 0) dan D(1, 2, 1). Hubungan antara garis m dan n adalah...
Soal 5
Terdapat sebuah kubus ABCDEFGH yang memiliki panjang rusuk 2 cm, diketahui rusuk AB memiliki beberapa rusuk yang sejajar lainnya, tentukan jumlah rusuk AB dan rusuk yang sejajar lainnya...
PEMBAHASAN
Soal 1 [br]Jika titik A berada pada garis k, maka secara notasi ditulis A ∈ [math]\alpha[/math], yang berarti titik A adalah bagian dari garis [math]\alpha[/math].[br][br]Soal 2[br]misalkan 4 titik tersebut adalag A, B, C, D maka akan membentuk garis AB, AC, AD, BC, BD, CD. maka terbentuk 6 garis.[br][br]Soal 3[br]Karena semua titik, termasuk D, memiliki z = 0, maka semuanya berada pada bidang z = 0, artinya D ∈ α.[br][br]Soal 4[br]Kedua garis tidak sejajar (arahnya sama tapi titik-titik tidak berada dalam bidang yang sama) dan tidak berpotongan. Maka garis m dan n adalah bersilangan (tidak sejajar, tidak berpotongan, tidak sebidang).[br][br]Soal 5[br]Jika digambarkan maka akan terlihat ada 3 garis yang sejajar dengan AB yaitu garis CD, EF, dan GH. maka totalnya ada 4 garis sehingga jumahnya 4[math]\times[/math]2 = 8 cm[br]
– SHEILA MEI LISA

5.2.

–

6.

Bab 6. Aplikasi Persamaan Garis Lurus

  • 1. APLIKASI PERSAMAAN GARIS LURUS

6.1.

APLIKASI PERSAMAAN GARIS LURUS

Perhatikan gambar berikut!
Sebuah tangga menuju lantai 2 disebuah rumah memiliki jarak tertinggi 350 cm dari lantai 1 dan jarak terjauh dari lemari adalah 500 cm. Berapa kemiringan dari tangga tersebut
Di salah satu kota S di Pulau Kalimantan, pertambahan penduduk tiap tahunnya selalu tetap. Pada tahun 2003 dan tahun 2009, jumlah penduduk di kota itu berturut-turut 300.000 orang dan 600.000 orang. Berapa jumlah penduduk di kota itu pada tahun 2015?
Perhatikan gambar berikut untuk mengerjakan Task 3 dan Task 4
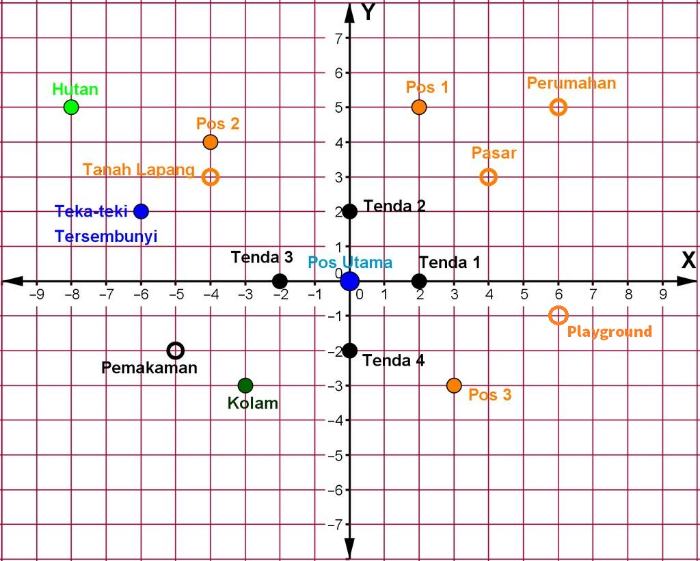
Jika 2 tempat dihubungkan dengan sebuah garis lurus, ada berapa pasang tempat yang sejajar degan sumbu [math]x[/math]? Sebutkan!
Jika 2 tempat di hubungkan dengan sebuah garis lurus, ada berapa pasang tempat yang sejajar dengan sumbu [math]y[/math]? Sebutkan!
– TjangElizabethMia

Informação