自然は意外と単純なのか？

[b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][br]アート、背景、実装、バリエーションの順に見ていきましょう。[br][/b][br][b][br][/b]

前回は花火のような粒子の動きを[br]運動法則のようなコードで[br]作ることができた。[br][br]今回は、生物の成長や動きのように、[br]一見複雑なアートが、[br]単純なルールに偶然がからむだけで疑似的に作られることを体験しよう。

今回のテーマは、[br][br][b][color=#0000ff][size=150]単純なルール　＋　偶然[br][/size][/color][/b][br]この発想や現象は、[br]さまざまなところで使われている。[br][br]ゲーム、音楽、賭け事、[br]いろいろあるね。[br][br]背景にあるのは、[br][br]単純なオブジェクト生成の「[b]ルール[/b]」と[br][br]偶然を生み出す「[b]乱数[/b]」だ。[br]１つずつ見てみよう。

１．背景

[size=150][b]ランダムウォーク、千鳥足というのがある。[br][br][/b][size=100]酔っ払いがまっすぐ前に歩けず、ふらふらと右へ左へ向きが定まらずに進むようすをさす。[br][/size][size=100]このルールは単純で、進行方向は右前か左前かのどちらか。[br]どっちに行くかは予測できない。[br]ここに乱数が使える。[br][/size][b][br]＜乱数の数学＞[br][/b][/size][br]乱数は数列だ。[br][br]一次合同式を作ってみる。[br][br][color=#0000ff][b][size=150]初項（乱数の種）をr0、[br]r[sub]n[/sub]=(a r[sub]n-1[/sub]+b) mod M　[br][/size][/b][/color][br]としよう。[br][br]数列が整数としたら、[b][color=#0000ff][size=150]法Mによる剰余は0からM-1のM通りだから、[br]いつかは剰余が同じになる[/size][/color][/b]。[br][br]だから、デタラメな出現に見えるようにするには、Mを巨大な数にすればよいね。[br]この発想のように、[b]一次合同式を使った疑似乱数を一様乱数[/b]uniform randomという。[br]なぜ、一様というかの理由は簡単で、０からM-1までの数が計算で出現するので、[br]基本的には、ゾーンに区切れば、出現の確率はどれも同じくらいになるはずだから。[br][br][color=#9900ff][b][u][size=150]質問：初項seedから一様乱数を生成するコードはどう作ればよいでしょうか。[br][/size][/u][/b][/color][br]一次合同式をf(x)=ax+b(mod M)　として、初項ｘ=seedとするとき、[br]geogebraなら、理論上はList=Iteration( f, seed, M)とします。[br]現実的には、f(x)=ax + bとおき、g(x) =f- floor( f /M) Mとします。[br]なぜか、Mod(f, M)とすると文法エラーがおきるバグがあるみたいです。[br]l1=iteration(g, seed, M)とすると、初項seedの数列がM+1番目までのリストになります。[br]そこで、l3=take(l1, 2, M+1)とすることで、seedのあとのM個の数列ができますね。[br]l2=unique(l3)とすると、重複のないリストになるね。[br][br]このl2の[b]サイズがM[/b]であるなら、[b]M個の乱数が重複なく出そろう[/b]ことになるね。[br][br]たとえば、a=[b]2[/b], b=3, M=[b]7[/b], seed=3とすると、集合｛０，２，３}で、[b]かたよる[/b]。[br]たとえば、a=[b]5[/b], b=3, M=[b]8[/b], seed=3とすると、集合｛0,1,2,3,4,5,6,7}で、[b]出そろう[/b]。[br][br][b][color=#0000ff][size=150]「aを８で割って５余る数、[br]bを奇数、[br]Mを2のべき乗の数[br][/size][/color][/b][br]にすると、一様にM個の剰余が出そろう。」[br]と言われています。[br][br]下のアプレットで、数値を変えて実験してみよう。[br]

一様乱数（実験用）

[b][size=150]＜乱数と言語＞[br][/size][/b][br]乱数は偶然性を生み出すのにとても便利だ。[br]まず、おもな用途は[br][br]A. 基本は０と１の間の小数を生み出す。[br]B. それを拡大して、０とaの間の小数を生み出す。[br]C. aからb未満の小数を一様に出す。[br]D. さいころをふるように、[b]整数[/b]のaからbまでが出る。b-a+1通りの整数を出す。[br][br]実際の言語では、どうなっているのだろうか？[br][br]・[b]processing[/b]では、pythonでもp5.jsでも同じ書き方。モジュールのインポートはなし。[br]A. ０以上１未満の小数を出す。[b]random[/b]()[br]B. 0以上a未満の小数を出す。 [b]random[/b](a)[br]B. aからｂ未満の小数をだす。[b]random[/b](a,b)[br]C. aから[b][u]ｂまで[/u][/b]の整数をだす。int([b]random[/b](a,b+1))[br][br]・ふつうの[b]python[/b]ではimport randomをして[br]A. ０以上１未満の小数を出す。random.[b]random[/b]()[br]B. ０以上a未満の小数を出す。random.[b]random[/b](0, a)[br]C. aからｂ未満の小数をだす。random.[b][color=#0000ff]uniform[/color][/b](a, b)[br]D. aから[b][u]ｂまで[/u][/b]の整数をだす。random.[b][color=#0000ff]randint[/color][/b](a, b)[br][b][color=#0000ff]使う関数が一種類ならば、from random import randintのようにかけば、random.はつけなくてよい。[br][/color][/b][br]・ふつうの[b]javascript[/b]では、モジュールなしだが、Math.をつける。[br]A. ０以上１未満の小数を出す。Math.[b]random[/b]()[br]B. ０以上a未満の小数を出す。Math.[b]random[/b]()*a[br]C. aからｂ未満の小数をだす。Math.[color=#0000ff][b]random[/b][/color]()*(b-a)+a[br]D. aから[b][u]ｂまで[/u][/b]の整数をだす。Math.floor(Math.[color=#0000ff][b]random[/b][/color]()*(b-a[b]+1[/b]))+a[br][br]それぞれの言語によって特徴があります。[br]processing関係の乱数はrandom関数1本で済みます。便利すぎですが、一般的ではありません。[br]ふつうのpythonは利用者も多いので、この関数を覚えるのがいいと思います。[br]一方でふつうのjavascriptも利用者が多いのですが、いちいち関数を加工する必要があります。[br]まあ、B,Cタイプなら、その場対応でなんとかなるでしょう。[br]しかし、Dタイプを使うときは、[br][b]アロー関数[/b]などで、次のように定義しておくと便利でしょう。[br][b][color=#0000ff]let randint = (a,b) => Math.floor(Math.random()*(b-a+1))+a;[br][/color][/b]こうするとrandint(1,6)と書くだけで、さいころの目関数として使えますね。[br]

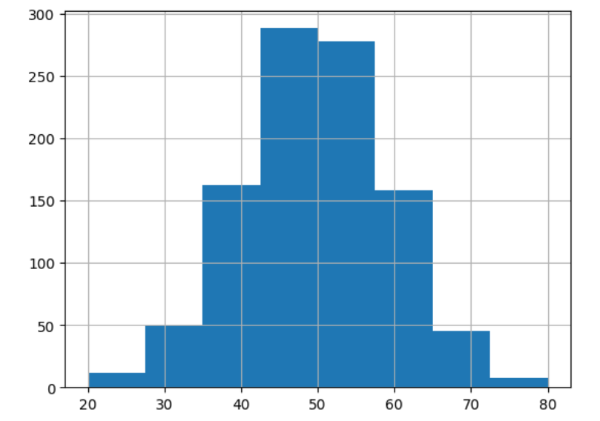
[b][size=150]＜正規乱数＞[/size][/b][br][br]乱数はゲームなどでは一様乱数ですむことが多いかもしれません。[br]でも、現実の世界では、一様よりも、中心にかたまる、正規分布の方が自然だ。[br]だからシミュレーションなどでは、正規分布する乱数が使われることが多い。[br][br][color=#9900ff][u][b][size=150]質問：0以上１未満を返す一様乱数random()から平均m,標準偏差sdの正規乱数を作るには、どうしたらよいでしょうか。[br][/size][/b][/u][/color][br]一様乱数はｘが０以上１未満のとき、確率密度関数f(x)=1/(1-0)=1となるね。[br]連続変数の分散と平均の出し方は、離散変数のΣを∫にしただけだから、Σで思い出して、積分に直そう。[br]平均はE(x)=Σｘp(x)=m,分散、つまり、偏差2乗の平均 V(x)=1/nΣ(x-m)2=.......=E(x[sup]2[/sup])-m[sup]2[/sup][br]だから、[br]ｘの平均はE(X)=[math]\int_0^1xf\left(x\right)dx=\int_0^1x\cdot1dx=\left[\frac{1}{2}x\right]^1_0=\frac{1}{2}=\mu[/math]　[br]ｘ2乗の平均はE(X[sup]2[/sup])=[math]\int_0^1x^2f\left(x\right)dx=\int_0^1x^2\cdot1dx=\left[\frac{1}{3}x^3\right]^1_0=\frac{1}{3}[/math]　[br]だから、ｘの分散は[math]V(X)=E(X^2)-μ^2=\frac{1}{3}-\left(\frac{1}{2}\right)^2=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}[/math]　[br]ということは、[br][b]「中心極限定理」[/b]から、どんな分布でも、平均値の確率分布は正規分布に収束するので、[br]一様乱数の平均値を振り続けると、正規分布に収束するでしょう。[br][br]一様乱数randomを12回ふった値の[b]合計res[/b]は、[br]平均が[math]\frac{1}{2}\cdot12=6[/math]、分散が[math]\frac{1}{12}\cdot12=1[/math] に近づき、その標準偏差がsd＝１の平方根＝１となる。[br][br]見かけは積分記号で一見すごそうにみえるけど、[br]ただのΣ計算、ただのたし算を連続変数化しただけで、もともと線形な処理だ。[br]だから、resに線形な処理をして、分散を変形できるはずだ。[br][br]たとえば、[b]res[/b]から6を引いて平均を０にする。[br]さらに、標準偏差sd、平均mを指定した正規分布になるようにするには、[br][b]res*sd+m[/b]をすると、正規乱数として返してくれるね。[br][br]たとえば、pythonでやってみよう。[br][br]#[IN]Python[br]#====================[br]# norm from uniform[br]import matplotlib.pyplot as plt[br]import pandas as pd[br]from random import random[br]counter = 1000[br][b]def norm(ave, sd ):[br][/b] res = 0[br] ans=0 ;[br][b] for i in range(12):[br] ans = random()[br] res +=ans[br] res -=6[br] return res *sd + ave[br][/b]def docalc():[br] ave = 50[br] sd = 10[br] data=[][br] for i in range(counter):[br] datai= norm(ave, sd)[br][b] data.append(datai)[br][/b] #print(data)[br] df = pd.Series(data)[br] df.hist(bins=8, range=[20, 80])[br] plt.show()[br]docalc()[br]のような処理を、言語の文法に合わせて実行すればよいでしょう。[br]一様分布関数から、正規分布に近い出力ができるね。[br][OUT]

[b][size=150]＜ルール＞[/size][/b][br]絵の部品になる図形に単純なルールを決めよう。[br][br]（ルール０）[br]・1個の点を画面の下（南）におく。[br]・点は1回で北東か北西に進む。どちらにするかはランダム。[br]・進んだ跡を画面にかく。[br]このルールでかくと、ランダムウォークに見えるアートができるでしょう。[br][br]（ルール１）[br]・円の1個目は中央におく。[br]・2個目からの円は平面にデタラメにばらまく。[br][b]・追加の円は、一番近い円に移動してから円を画面にかく[/b]。[br]このルールでかくと、[b]冒頭の「植物の枝の成長」[/b]のように見えるアートができます。[br][br]（ルール２）[br]・円の1個目は中央におく。[br]・2個目からの円は平面にデタラメにばらまく。[br][b]・追加の円は、他の円に重ならない大きさの円を画面にかく[/b]。[br]このルールでかくと、円の隙間がどんどん埋められていくアートができるでしょう。[br][br]（ルール３）[br]・円は８方位に毎回ランダムに移動できる。[br]・移動したら、移動したあとを画面にかく。[br]このルールでかくと、ランダムウォークの8方位バージョンのアートができるでしょう。[br][br]あとは、図形や線にランダムまたは、位置に応じた色をつけることで、[br]さらにアートに変化がでるでしょう。

２．実装

ルール１を実装することで、[br]冒頭の図をかいてみよう。[br][br][b][size=150]＜pyhon in processing＞[/size][/b][br]'use strict';[br]maxCount = 5000 # max count of the cirlces[br]currentCount = 1[br]x = [][br]y = [][br]r = [][br]def setup():[br] size(800, 800)[br] strokeWeight(0.5)[br] # first circle[br] x.append( width/ 2)[br] y.append( height/2)[br] r.append(10)[br]def draw():[br] global currentCount, x,y,r[br] background(255)[br] newR = random(1, 7)[br] newX = random(newR, width - newR)[br] newY = random(newR, height - newR)[br] closestDist = 99999999999999999999 #max of distance[br] closestIndex = 0[br] for i in range(currentCount):[br] newDist = dist(newX, newY, x[i], y[i])[br] if newDist < closestDist:[br] closestDist = newDist[br] closestIndex = i[br] angle = atan2(newY - y[closestIndex],newX - x[closestIndex])[br] x.append( x[closestIndex] + cos(angle)*(r[closestIndex] + newR))[br] y.append( y[closestIndex] + sin(angle)*(r[closestIndex] + newR))[br] r.append( newR )[br] currentCount +=1[br] for i in range(currentCount):[br] fill(255*x[i]/width,255*y[i]/height,255*r[i]/7) #rule for coloring[br] ellipse(x[i], y[i], r[i]*2, r[i]*2) #draw circle[br] if currentCount >= maxCount:[br] noLoop()[br][br]単純で行数も少なく冒頭のキレイなアートができる。[br]しかし、意味が分かりにくいので、javascriptでクラスを使ってかき、[br]geogebraで動くようにしよう。[br][br]前回と同様に、javascriptで円のクラスを定義する。クラス利用（生成と描画）を分離してかく。[br]（円の定義）[br]コンストラクター（生成関数）で決めよう。[br]半径Rは１から７、X座標はー(画面横幅-円の半径)から(画面横幅-円の半径)とするこで、[br]円が画面から切れないようにする。Y座標も同様にしよう。[br]円の色、R,G,Bは255を最大に対して、200,100,50にして、茶色っぽくする。[br]円の連番は０番にかりに入れる。[br]・setId関数で円の連番をあとで設定できるようにする。[br]・setRXY関数で円のサイズR,座標X,Yをあとで変更できるようにする。[br]・neaness(other)関数で、他の円otherとの距離の2乗を求める。一番近い円を探すときに使おう。[br]・[b][color=#0000ff]approach(other)関数[/color][/b]で、他の円otherとの中心を結ぶ線にそって、中心どうしの距離が、[br]半径の和（this.R+other.R)になるまでくっつくときに、自分のX,Y座標を計算して更新する。つまり、くっつける。このスライドをするための角度angleを中心を結ぶ線を斜辺とする直角三角形のｘ方向の長さとｙ方向の長さから、そのatanから求めます。Math.atan2関数が使えます。[br]下の図のように、[br]this.Xは、半径の和のcos(angle)だけother.Xたし、[br]this.Yは、半径和のsin(angle)だけother.Yにたします。[br]・draw(app)関数で、1個の円をかきます。[br]画面のappletのオブジェクトを受け取り、アプレット画面に対する描画関係のAPI関数を使う。[br]円を1個かき、fillを１にして中もそめる。ラベルなし、軸なし、格子線なしにする。[br][br]（円の利用）[br]リセットボタンを押す(OnClicked)と、setup関数を実行します。[br]画面には隠れてますがスラーダーtがアニメーションで動き、最新情報(OnUpdate)でdraw関数を実行します。このdrawは円の１こずつのdrawではなく、画面全体のdrawにかかわります。[br]・setup関数で画面サイズをwidth,heigtともに600になるようにしつつ、原点が中央にくるようにします。[br]1個目の円を描く前に、書いてある円をぜんぶ削除します。1個目の円は半径10で原点を中心にかく。[br]・draw関数で、追加の円をかきます。追加円と既存円との近さを求めて、一番近い円の番号が[br]　closestIIndexです。この番号の円に追加した円をapproachします。[br]それから、追加円のdrawをしましょう。[br]・円の集まりリストcirclesに円のインスタンスを追加したり、円の番号をセットするsetIDなどの[br]タイミングがずれると、ちがう絵になったりするので、このあたりの検証は[br]前回紹介した、VSコードでgeogebra のwebへの埋め込みなどでデバックするといいね。[br][br]冗長にはなるけれども、手続き処理をする書き方よりも、改造がしやすい利点があるね。

approach法

[b][size=150]＜geogebra　by 　javascript ＞[br][/size][/b][br]let windowggbApplet = ggbApplet;[br]'use strict';[br]let circles = []; // 円たち[br]const maxCount = 5000; // max count of the cirlces[br]let currentCount = 1;[br]let width = 600;[br]let height = 600;[br]let randint = (a,b) => Math.floor(Math.random()*(b-a+1))+a;[br][br]function ggbOnInit() {[br] setup();[br]}[br]class Circle {[br] constructor() {[br] this.R = randint(1,7);[br] this.X = randint(this.R - width , width - this.R);[br] this.Y = randint(this.R - height, height - this.R);[br] this.colR= 200;[br] this.colG= 100;[br] this.colB= 50;[br] this.num = 0;[br] }[br] setId(num){[br] this.num =num;[br] }[br] setRXY(r,x,y) {[br] this.R = r;[br] this.X = x;[br] this.Y = y;[br] }[br] nearness(other){[br] return Math.pow((this.X- other.X),2) + Math.pow((this.Y- other.Y),2);[br] }[br] aproach(other){[br] let angle = Math.atan2(this.Y - other.Y, this.X - other.X);[br] this.X= other.X + Math.cos(angle) * (other.R + this.R);[br] this.Y= other.Y + Math.sin(angle) * (other.R + this.R);[br] this.colR= this.X *255/width+122;[br] this.colG= this.Y *255/height+122;[br] this.colB= this.R *255/7+122;[br][br] }[br] draw(app){[br] let posinfo = `c${this.num} = Circle(Point({${this.X},${this.Y}}),${this.R})`;[br] app.evalCommand(posinfo);[br] app.setColor("c"+this.num, this.colR, this.colG, this.colB);[br] app.setFilling("c"+this.num,1);//fillingout[br] app.setLabelVisible("c"+this.num,false);//NO label[br] app.setAxesVisible(false,false);//No Axes[br] app.setGridVisible(false);//No Grid[br] }[br]}[br][br]function setup() {[br] // 既存の点cオブジェクトあれば削除[br] if (circles.length > 0) {[br] for (let i = 0; i < circles.length; i++) {[br] windowggbApplet.deleteObject("c" + i);[br] }[br] }[br] currentCount = 1;[br] circles = [ ];[br] windowggbApplet.setCoordSystem(- width/2, width/2, - height/2, height/2);[br] //1個目の円をかく。[br] let firstC = new Circle();[br] firstC.setId(0);[br] firstC.setRXY(10,0,0);[br] circles[0] = firstC;[br] firstC.draw(windowggbApplet);[br]}[br][br]function draw() {[br] //円の追加[br] let closestDist = Number.MAX_VALUE;[br] let closestIndex = 0;[br] let newC = new Circle();[br] // 追加円に、もっとも近い円を探す。[br] for (let i = 0; i < currentCount; i++) {[br] let target = circles[i];[br] let newDist = newC.nearness(target);[br] if (newDist < closestDist) {[br] closestDist = newDist;[br] closestIndex = i;[br] }[br] }[br] //追加円をかく。[br] newC.setId(currentCount);[br] newC.aproach(circles[closestIndex]);[br] circles[currentCount] = newC;[br] newC.draw(windowggbApplet);[br] currentCount++;[br]}

３．バリエーション

[br][color=#9900ff][u][b][size=200][size=150]質問：ルール２のように、円が重ならないように増えていくようにするにはどのようなコードにしたらよいでしょうか。[br][/size][/size][/b][/u][/color][br]円をばらまくところはルール１と同じです。[br]ただ、円に重ならないようにするしくみを作る必要がありますね。[br]まず、円のコンストラクタで半径を50にしますが、最低半径は２にします。[br]そうすると、追加したい円thisと既存の円otherとの隙間がないと追加したものを無効にしましょう。[br][br] centerDist(other){ return Math.sqrt(Math.pow((this.X- other.X),2) + Math.pow((this.Y- other.Y),2));}で中心距離を求めます。[br]circumDist(other){return this.centerDist(other) - other.R -2;}周囲と周囲との最大のすきまを求めます。[br]noRest(other){return this.circumDist(other)<0 ? true: false;}は隙間がないときにtrueです。[br]もし、既存の円全部を調べて、追加するすきまがあれば、[br]一番隙間の狭い円に対して、標準半径50と最低半径２の間でくっつけらたらくっつける調整をします。[br]fit(other){[br] let maxR = this.centerDist(other) - other.R; [br] let res= (minR<=maxR)? true: false;[br]　if(res){[br]　　　if (maxR < this.R) {[br]　　　　　　this.R = maxR;[br]　　　}[br]　} [br]　return res;[br]}[br]可能な最大半径をmaxRとして、minR=2以下ならfitは成功とします。さらに、maxRが50を切っているなら[br]半径を50からmaxRに更新して、隙間にぴったり詰め込めばよいですね。[br][br]理論上はこれを、drawで実行すると、毎回円を追加するたびに、隙間に入ります。[br]実際、VSコードとｊｓでwebにgeogebraアプレットを埋め込みができます。[br]しかし、これを素のgeogebraアプレットのスクリプト記述に貼り付けても[br]必ず動く保証はありません。[br]ここでは、上のアプレットをコピーして、グローバルjavaスクリプトに貼り付けただけですが、[br]最初は動きませんでした。しかし、スライダーの最新情報のjavascriptにalert("draw ");を入れたら動きました。[br]意味がわかりませんね。[br]同一シートにjavascriptのアプレットが２つ以上あると内部動作が不安定になるとか、裏で動いているgeogebraの謎の機構によるものと思われます。[br][br]参考までに、下に貼り付けたコードをのせておきますね。[br]

重ならない円が増殖する