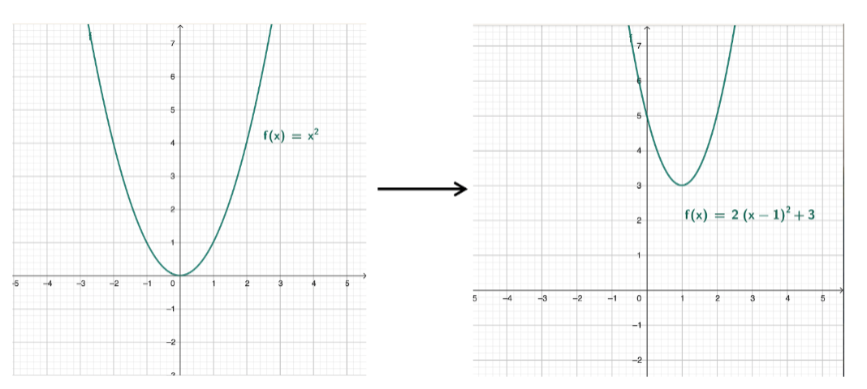
Du kennst schon den Graphen der Funktion [math]f\left(x\right)=x^2[/math]. Wenn du in deren Funktionsterm Faktoren oder Summanden änderst, verändert sich auch der dazugehörige Graph. Zum Beispiel zu [math]f\left(x\right)=2\cdot\left(x-1\right)^2+3[/math].

[size=100][size=150]Aufgabe 2[/size][/size][br][br]Wenn du im Funktionterm [math]f\left(x\right)=a\left(x+b\right)^2+c[/math] die Werte für den Faktor [math]a[/math] oder die Summanden [math]b[/math] oder [math]c[/math] änderst, so ändert sich auch der dazugehörige Graph. Untersuche nun mithilfe der Schieberegler in dem folgenden Funktionsplotter, wie sich der Graph der Funktion verändert.[br][br]Diese Schritte können hilfreich dabei sein:[br][br]- Betrachte zuerst Änderungen am Summanden [math]c[/math]. Nimm hierfür die Funktion [math]f\left(x\right)=1\left(x+0\right)^2+c[/math] und verändere die Werte von [math]c[/math] mithilfe des Schiebereglers.[br][br]- Betrachte anschließend Änderungen am Faktor [math]a[/math]. Nimm hierfür die Funktion [math]f\left(x\right)=a\left(x+0\right)^2+0[/math] und verändere die Werte von [math]a[/math] mithilfe des Schiebereglers.[br][br]- Betrachte dann Änderungen am Summanden [math]b[/math]. Nimm hierfür die Funktion [math]f\left(x\right)=1\left(x+b\right)^2+0[/math] und verändere die Werte von [math]b[/math] mithilfe des Schiebereglers.[br][br]Untersuche zunächst nur den [i]Funktionsgraphen[/i]. Beobachte später auch, welchen Einfluss [math]a[/math], [math]b[/math] und [math]c[/math] auf die [i]Wertetabelle[/i] haben (Klicke auf "Wertetabelle anzeigen").

Versuche nun, deine Erkenntnisse aus Aufgabe 2 zu begründen.[br][br]Die folgenden Schritte können hilfreich sein:[br][br]- Begründe den Einfluss von [math]c[/math]. Elise findet, dass der Graph im folgenden Bild enger wird durch den Parameter [math]c[/math]. Marcus sagt, dass die Form des Graphen unverändert bleibt. Wer hat recht? Versuche, das mit der Wertetabelle zu begründen.

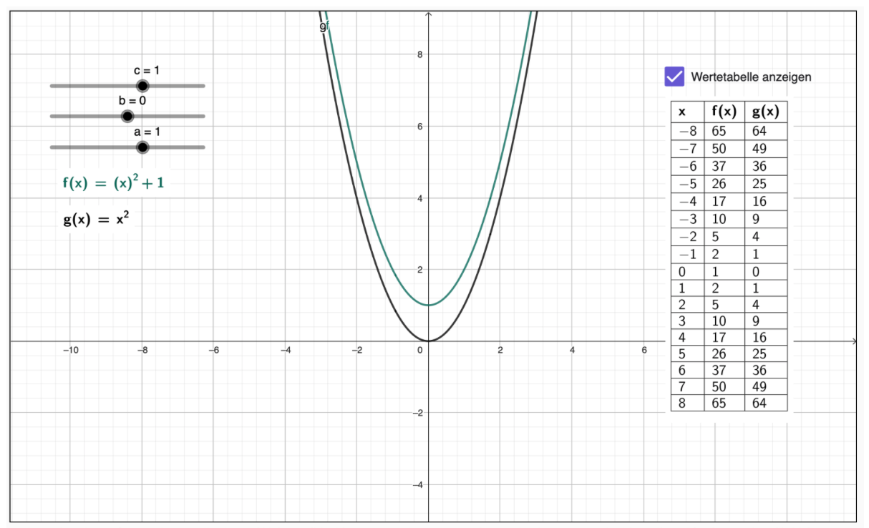
- Begründe den Einfluss von [math]a[/math]. Vergleiche dafür die erzeugten Graphen aus Aufgabe 2 und vergleiche sie mit der Normalparabel. Beschreibe genau, wie sich der Graph verändert und wieso. Betrachte dafür auch die Wertetabellen: Was ist z.B. der Unterschied zwischen [math]a=0.5[/math] und [math]a=2[/math] in den dazugehörigen Wertetabellen? Was ist die Ursache dafür?[br][br]- Begründe den Einfluss von [math]b[/math]. Schaue dir die Graphen der Funktionen [math]g\left(x\right)=x^2[/math] und [math]f\left(x\right)=1\left(x-1\right)^2+0[/math] gleichzeitig an und vollziehe die folgenden richtigen Aussagen nach: [list][*]"Wenn man sich [math]1\left(x-1\right)^2+0[/math] statt [math]x^2[/math] anschaut, werden alle Werte in der Tabelle in Richtung größerer [math]x[/math] verschoben." [/*][*]"Für [math]x=3[/math] gilt [math]x^2=9[/math], aber erst für [math]x=4[/math] gilt [math]1\left(x-1\right)^2+0=9[/math]."[br][/*][/list]

Erstelle ein Merkblatt mit allen Erkenntnissen, Ergebnissen und Begründungen aus den Aufgaben 1 bis 3.[br]Stell dir hierfür vor, du würdest einen Spickzettel für deine/-n Freund/-in schreiben, die in der heutigen Stunde nicht dabei war und eine Klassenarbeit über das Thema schreibt.

_______________________________________________________________________________________[br][br]Die Aufgaben stammen aus den Materialien von Lisa Göbel und Bärbel Barzel:[br][br]Göbel, L. & Barzel, B. (2021): Parameter digital entdecken - wirklich so easy? [i]Mathematik lehren, 226[/i], 20-24.[br]Göbel, L. (2021). [i]Technology‑Assisted Guided Discovery to Support Learning: Investigating the Role of Parameters in Quadratic Functions[/i] (1 . Aufl.). Springer Spektrum Wiesbaden. https://doi.org/10.1007/978-3-658-32637-1