Az alábbi feladatot [url=https://math.bme.hu/diffe/staff/hujter.shtml]Hujter Mihály[/url] fedezte fel König Dénes jegyzeteiben. Eszerint a feladatot [url=https://hu.wikipedia.org/wiki/K%C5%91nig_D%C3%A9nes]Kőnig Dénes[/url] és [url=https://hu.wikipedia.org/wiki/Egerv%C3%A1ry_Jen%C5%91]Egerváry Jenő[/url] ismerte, szerkesztette 1941-ben:[br]

85/b Egy körbeírt[i] ABCDEF[/i] hatszög [i]AB, CD[/i] és EF oldala egyenlő a kör sugarával. Bebizonyítandó, hogy a másik három oldal felezőpontjai szabályos háromszöget alkotnak. [br] (Egerváry, K. D.)
E feladat kapcsán [url=https://www.math.u-szeged.hu/mathweb/index.php/hu/munkatarsaink?id=18&bolyaiid=17]Gévay Gábor[/url] megtalálta az interneten -[url=https://paws.kettering.edu/~bmccarti/] Brian J. McCartin[/url] a [url=https://www.m-hikari.com/mccartin-2.pdf]Mysteries of the Equilateral Trinagle [/url] (2010) című könyvét, amelynek a 64. oldalán a szerző ezt az összefüggést [i]propeller tétel[/i]nek nevezte. Ebben a szerző hivatkozott [url=https://hu.wikipedia.org/wiki/Martin_Gardner]Martin Gardner[/url] [url=https://old.maa.org/press/maa-reviews/a-gardners-workout-training-the-mind-and-entertaining-the-spirit]A Gardner's workout Training Mind and Entertraining the Spirit [/url] ( Az elme edzése és a lélek szórakoztatása) . című könyvére, ahol Gardner egy egész fejezetet szánt a címben jelzett témának. (Chapter 33. pp.: 241.-253.) McCartin három rajzot vett át Gardner könyvéből. Mi is ezt tesszük, az első öt ábrát átvéve és kiegészítve Gardner igen izgalmas kommentárjával:
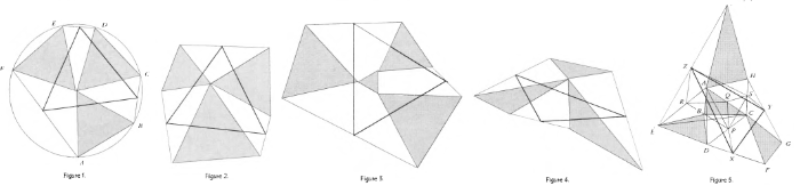
[br][br][i]"A néhai [url=https://en.wikipedia.org/wiki/Leon_Bankoff]Leon Bankoff[/url] (1997-ben halt meg) a kaliforniai Beverly Hillsben élő fogorvos, aki emellett a síkgeometria világszinten elismert szakértője is volt.1979-ben mesélt nekem egy sor lenyűgöző felfedezéséről, amit az általa aszimmetrikus propeller-tételnek nevezett tétellel kapcsolatban tett. Szándékában állt ezeket egy cikkben tárgyalni, de soha nem jutott el odáig, hogy megtegye. Ez egy összefoglalása annak, amit elmondott nekem. Az eredeti propeller-tétel legalább az 1930-as évek elejére nyúlik vissza, és ismeretlen eredetű. Három egybevágó egyenlő oldalú háromszögre vonatkozik, amelyek csúcsai egy [i]pontban találkoznak, mint az [/i]az 1. ábrán árnyékolva látható A háromszögeknek, amelyek egy propeller lapátjaira hasonlítanak, nem kell szimmetrikus mintát alkotniuk, hanem bármilyen helyzetben lehetnek. Egymáshoz érhetnek, vagy akár át is fedhetik egymást. [/i]A[i] BC, DE és FA szakaszokat úgy rajzoljuk meg, hogy egy körbe írt hatszöget alkossanak. A három szakasz felezőpontjai egy egyenlő oldalú háromszög csúcsai. A tétel komplex számokat használó bizonyítása az évente megrendezett [url=https://maa.org/putnam/]William Lowell Putnam verseny [/url]B-1. feladatának megoldásaként jelent meg.[br][url=https://en.wikipedia.org/wiki/Harold_Scott_MacDonald_Coxeter]H. S. M. Coxeter[/url] a bizonyítást egy karácsonyi üdvözlőlapon küldte el Bankoffnak, és megkérdezte tőle, hogy tud-e euklideszi bizonyítást adni a tételre. Bankoffnak nem okozott nehézséget ilyen bizonyítást találni. [url=https://users.renyi.hu/~p_erdos/1973-28.pdf]"Az aszimmetrikus propeller" [/url] című dolgozatban Bankoff, [url=https://hu.wikipedia.org/wiki/Erd%C5%91s_P%C3%A1l]Erdös Pál[/url] és[url=https://en.wikipedia.org/wiki/Murray_S._Klamkin] Murray Klamkin[/url] elkészítette a tétel első általánosítását. [br][br]Megmutatták, hogy a három egyenlő oldalú háromszögnek nem kell egybevágónak lennie. Bármilyen méretűek lehetnek, ahogy a 2. ábrán látható, és a tétel akkor is érvényes. Két bizonyítást adnak, az egyik egy egyszerű euklideszi bizonyítás, a másik komplex számokkal kapcsolatos. Mint korábban, és minden későbbi kiterjesztésben, a háromszögek érintkezhetnek egymással, vagy akár át is fedhetik egymást.[br][br]Később Bankoff három további általánosítást tett. Tudomásom szerint ezeket nem publikálták. [br][br]Második általánosítás: A propeller-háromszögeknek nem kell egy csúcsban találkozniuk Találkozhatnak bármelyik egyenlő oldalú háromszög csúcsában, ahogyan a 3. ábrán látható. [br][br]Harmadik általánosítás: A propeller-háromszögeknek nem kell szabályosaknak lenniük. Elegendő, hogy azonos körüljárású hasonló háromszögek legyenek.[br][br][br]Negyedik általánosítás: A hasonló háromszögeknek nem kell egy pontban találkozniuk! Ha a légcsavarok egy tetszőleges méretű negyedik háromszöghöz csatlakoznak úgy hogy a közös csúcshoz tartozó szögek egyenlők legyenek.[br][br]Bankoff 1973-ban bizonyította - elemi úton - a propeller tételnek ezt a végső, általánosítását."[br][/i][br][right]M. Gardner[/right]
A fenti applet szabad pontjait alaposan megmozgatva tapasztalhatjuk, hogy a bizonyítandó állítás nem függ az adott háromszögek kölcsönös helyzetétől, lehet közös belső pontjuk is. Így meggyőződhetnek olvasóink arról, hogy a feladat metrikus és illeszkedési feltételei, relációi valóban általánosabb összefüggések, mint ahogy ezt egy-egy statikus rajz tükrözheti. [br][br] Kimondhatjuk, hogy az ötödik - legáltalánosabb - változat két különböző speciális esete a harmadik és negyedik, a harmadiknak a második, és annak az első. Így nyilvánvalóan elegendő a ötödiket igazolni, amely például így fogalmazható meg:[br][list][*][i]Legyen adott a sík négy azonos körüljárású háromszöge, amelyek közül egynek a csúcsai egybeesnek a másik három nekik megfelelő, azaz egybevágó szögekhez tartozó csúcsával. Mutassuk meg, hogy e három háromszög szabadon maradó, egymásnak megfelelő csúcsait összekötő szakaszok felezőpontjai is az adottakhoz hasonló háromszöget alkotnak![/i][/*][/list]
Olvasóink minden bizonnyal többször tapasztalták, hogy az "elemi" jelző nem az "egyszerű" szinonimája. [br]Joggal nehezményezhető - [url=https://acta.bibl.u-szeged.hu/64235/]mint azt e sorok írója meg is tette[/url] - , hogy olykor egy - egy szép probléma még szebb megoldása gyakran úgy kerül elénk, mint ahogy a bűvész elővarázsolja a nyuszit az üres cilinderből, a nagyérdemű publikum legnagyobb ámulatára. [br][br]Nem szokás közzé tenni azokat az olykor eredménytelen, vagy csak túl bonyolult, esetleg nagyobb matematikai apparátust igénybe vevő megoldásokat, amelyeknél van szebb, elegánsabb. [br][br]Mi is itt a probléma legáltalánosabb változatának a - minden bizonnyal - legszebb elemi geometriai megoldását mutatjuk be, L. Bankoff gondolatmenetét követve.[br][br]Azonban akit érdekelnek az ide vezető előzmények és következmények, megismerkedhetnek néhány ezt bemutató GeoGebra munkalappal. [br][list][*][url=https://www.geogebra.org/m/zb5butty]Itt bemutatunk[/url] egy elemi megoldást a legspeciálisabb első esetre. A munka szépséghibája, hogy - jobb ötlet híján - hivatkoznunk kellett egy [url=https://www.geogebra.org/m/xjjq7afa]talán kevésbé ismert elemi geometriai összefüggés[/url]re, amely ugyancsak igényelte az elemi bizonyítást.[br][br][/*][*][url=https://www.geogebra.org/m/umphuzqz]Itt bemutatunk[/url] egy elemi bizonyítást a második és harmadik esetre, amelyhez készíteni kellett néhány olyan - ugyancsak elemi - lemmát. Azért, hogy a harmadik esetet visszavezethessük a könnyebben igazolható másodikra. [br][br][/*][*][url=https://www.geogebra.org/m/swk9zjys]Itt[/url] és [url=https://www.geogebra.org/m/ku3acxnb]itt bemutatjuk[/url] az eddigi összefüggések egy - talán újdonságnak tekinthető - következményét, "a nagyérdemű publikum legnagyobb ámulatára". [/*][/list][br]A probléma alábbi szép, lépésről lépésre jól követhető megoldása remélhetőleg meggyőzi olvasóinkat arról - mint ahogy e sorok íróját is meggyőzte -, hogy Bankoff fogorvos úr ezzel a problémával - és megoldásával - joggal vívta ki azt a lehetőséget, hogy erről közös cikket írjon Erdős Pállal. [br][br]Minden bizonnyal kevés olyan ember van a matematikát hivatásként művelő, abból élő "szakmai körön" kívül, aki azzal büszkélkedhet, hogy az [url=https://hu.wikipedia.org/wiki/Erd%C5%91s-sz%C3%A1m]"Erdős száma" [b][size=150]1.[/size][/b][/url] [br][br]Nos, ismerkedjünk meg az általános propeller tétel Bankoff-féle bizonyításával.
[list=1][*][b]A feladat:[/b] [br]Bizonyítandó, hogy ha az [i]ABC, AHJ, DBE[/i] és[i] FGC[/i] azonos körüljárású hasonló háromszögek, akkor a [i]DF, GH [/i]és [i]JE[/i] szakaszok [i]X, Y, Z [/i]felezőpontjai a másik négyhez hasonló háromszög csúcsai. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWQAAAGXCAIAAAALf73AAAAgAElEQVR4Ae2dB5gVRdq2519dvtVFQBABWV0VUTCsaw6LmH8QGEQBERUUFSQoSBAR4UN0QRwxgAEUA4iySDYgKIKILKLMIDmK5GFgCAMDDBOfj1PN1Jw5fbpPh+ruqj4vF5fW6a74VPVNVfXbb6WA/pACpAApYEGBFAtxKAopQAqQAiBY0CAgBUgBSwoQLCzJRJFIAVKAYEFjgBQgBSwpQLCwJBNFIgVIAYIFjQFSgBSwpADBwpJMFIkUIAUIFjQGSAFSwJICBAtLMlEkUoAUIFjQGCAFSAFLChAsLMlEkUgBUoBgQWOAFCAFLClAsLAkE0UiBUgBggWNgSAVSE0NsnQq25YCBAtbclHkxArMmTPnuecGdOr05Icffpibm2uegGBhro9UdwkWUnWH2pU5evRo8+atzzzz0vr1X7r00rfOP/++s846Pz093aRVBAsTcWS7RbCQrUcUrk+3bk+fe26bpk0LUlOh/b366qlnnXX+oUOHjFpFsDBSRsLrBAsJO0XJKh06dOiUUyo3bpzDSaEFzj//gdGjRxs1iWBhpIyE1wkWEnaKklX68ccfzzmnYQwpUlNx+eVj2rV73KhJBAsjZSS8TrCQsFOUrNJvv/1Wq9Y/9bC45JLXunfvHd2kxx7D4cORC4WFaNky+g6FpVaAYCF19yhUucLCwipVzrz55hXRvGjWrPiss66bMWNGdEP69sXkyTh6FF99hT59ou9QWGoFCBZSd49alfvkk/FnnFH/lltWabxo0uTIBRd0vPnmRjGt+OMPPP10ZE7x9NP444+Ym/RTXgUIFvL2jYo1Gzt2XOXKNSpWvObcc5udfHLVRo0ePXjwoIoNoTrrFSBY6DWhK64UmD0777LLlnzyydd9++596CFXWVFiqRQgWEjVHWGoTFoaOnZEZibWrkWVKsjODkOjqA0AnRtCo0C0Am3a4K23IrDIzETbtkhLE10A5ReQAjSzCEj4cBSbC7wd25I6dfDjjydg8c03OP98lJTExqHfKipAsFCx1+Socy7QDdhbrjIHDqBiRezYcQIWmZn45z8xa1a5OPRDUQUIFop2XNDVjkcKAPPm4frry0iRmYnXX498J0J/QqAAwSIEneh7EwxIAUR2KLTdTW3PIjMTmzahWjVs3ep7JalA0QoQLEQrGvr8jEkBIHp3k/OiUyc8/3zodQl/AwkW4e9jkS00JQWA6N1NDouffkLNmigoEFkRyst/BQgW/muucomrYnc0oxuj393kvGjYEBMnRselsHoKECzU6zNpa6zf3eSwGDMGDRtKW3GqmCUFCBaWZKJIVhTQ725yWGzbhlq1sGqVlWwojqQKECwk7RgVqxV3d5PzondvdOumYrOozicUIFjQUBCmQNzdTQ6LpUtRteoJtzfCiqSMfFSAYOGj2MoVdcxGjU12NzkvmjbFe+/ZyJOiSqUAwUKq7pCpMtpbUub/zkq1THY3OSw+/xyXX24lM4ojowIECxl7Jfg6JbKn0NfQZHeTw2LnzoghxqJF+tR0RQEFCBYKdJLfVbRPCiPbTY4JHnjhBZBHHL87VFB5BAtBQoYmG0ekMLLd5IzgAfKIo+5IIVio23ce1NwpKazsbnJekEccD3rOjywJFn6orEYZ+XH8U1isuZXdTQ4L8ohjUVXZohEsZOuRQOuT57B0K7ubHBbkEcehykEnI1gE3QOhKN/cdjMaE1qYPOKo2O0ECxV7Tbo6m9tu6mFBHnGk60ILFSJYWBCJopgqYGt3k4ODPOKYiirjTYKFjL2iVp1s7W5yWJBHHLV6mc4NUa6/xFU4F1gmJje7u5ucF+QRR0wH+JULzSz8UlqqcpzaU8RthN3dTQ4L8ogTV09pLxIspO0azyomlBTWbTc5I3iAPOJ41seeZEyw8ERWeTMVTQpnu5ucF+QRR96hoqsZwUInSYgviCZF3FOFOAisBMgjjkLDjWChUGe5q6oHpIh7qpAVRkTHIY847vrVv9QEC/+0Drik0WZe/B3XzfHuJucFecRxLL7PCQkWPgsetuLs2m5yRvAAecRRZUwQLFTpKRnr6XJ3k/OCPOLI2Lu6OhEsdJLQBcsKOLPd5IzgAfKIY1nyICMSLIJUX/WyHdtuckzwAHnEkX8wECzk7yN5a+h+d5PDgjziyNvNpTUjWJQqEab/5wLv+NEe97ubHBbkEcePDnNXBsHCnX4SpvbGnkLfUFG7m5wX5BFHL7JUVwgWUnWH68r4RQr3tpucETxAHnFcd7+3GRAsvNXX19x9JIUQ202OCR4gjzi+DhibhREsbAombXR/SWH9VCEOAisB8ogj7fgi5zcyd42duvlOCjdfpptTgzzi2Ol4X+PSzMJXub0qbKUn332Y1Fb47iYnCHnEMZE92FsEi2D1V7V0UbabnBE8QB5xpB0TBAtpu0bqigm03eSY4AHyiCNn3xMs5OwX2Wsl0HaTM4IHyCOOnN1PsJCzX2SvlVjbTY4JHiCPOBKOAIKFhJ2SqErHEkXw+L53u5scFuQRx+M+dJI9wcKJakGm0d6SHg6yCt7tbnJYkEecIDvYoGyChYEwcl4Owp5Cr4Snu5ucF+QRR698sFcIFsHqb6d0OUjhke0mZwQPkEccO4PDj7gECz9UFlCGNKTwznaTY4IHyCOOgJEjLguChTgtvctJJlL4sLvJYUEecbwbUw5yJlg4EM3fJPlAN7+tuU1a6MPuJocFecQx6Qj/bxEs/Nfcfol59pN4lsKf3U3OC/KI41lP2s6YYGFbsiRP4KntJmcED5BHHHnGG8FCnr5QoyZe225yTPAAecSRZGQQLCTpCDWq4efuJocFecSRZHAQLCTpCDWq4fPuJucFecSRYXwQLGTohag65ALLon5KFvR5d5PDgjziyDAQCBYy9EJpHWSypyitU7n/+7y7yWFBHnHKdUNAPwgWAQmvL1Z6Uvhpu8kxwQPkEUc/ZHy+QrDwWXCD4lQgRSC7mxwW5BHHYOj4d5lg4Z/WhiWpQAovThXiILAYII84hkPIlxsEC19kNilEEVJ4dKqQRUxo0cgjjsk48uEWwcIHkU2LGCXRdx+mFUVQu5scKOQRx7yDvL5LsPBa4fDk77/tJscED5BHnADHE8EiQPFVKjrY3U0OC/KIE+CgIVgEKL5KRQdlu8kxwQPkESeocUOwCEp5xcoNynaTM4IHyCNOUEOHYBGU8oqVG/juJocFecQJaugQLHxUPhd4x8fihBYlw+4m5wV5xBHat1YzI1hYVcptPHXsKfQtlWR3k8OCPOLo+8iHKwQLeyKnlP/TokULS+lVJoUMtpscEzxAHnEsDTyhkQgWDuXMzs6uX7/+zp07E6dXnBQy2G5yRvAAecRJPPBExyBYOFS0ZcuWn332WeLE6pPCt1OFOAgsBsgjTuLhJzQGwcKJnJ9++mnLli0TpwwFKYL9Mt0EHOQRJ/EIFBqDYGFbzszMzHr16mVnZydOuVKZ7z5M2iLb7ibHB3nEMek1L24RLGyr2qRJk+nTp8dN1qhRo1mzZsW9pe5FeWw3OSZ4gDzi+DmuCBb21B4zZkz79u3jpunRo0dKSkrFihXXrVsXN4KiF+Wx3eSM4AHyiOPnoCJY2FB7y5YtF198cU5Ojj7Nc889l5KScv/999esWbNWrVph4oVUtpscEzxAHnH0o9GjKwQLG8I2bdq0vJlF5BeAW265JSUlpUuXLiUflqz5Yk3NmjVPO+200KxHpLLd5IzgAfKIY2MEu4tKsHCnH7B69eo//elPp5566trla1EPuBydmnVKSUm58cYb3WYtQXppdzc5LMgjjm/DhGAhQOr58+fXrFGz1qm11j297rlqkfVI++vaF+cVC8g66Cxk3t3kvCCPOP4ME4KFCJ1zseaBNTXPrFnx1IqR9chVXUqal6AHsEtE5oHmIfPuJocFecTxZ4wQLFzrXGp5tXDhwj/96U9XVruyZEgJ0oEHgDbAf13nH2gGku9ucl6QRxwfhgnBwp3IpaTQclm6dGnxe8VoCRwBsoE+QCrwPlDkrpTgUku+u8lhQR5xfBgjBAsXIpcnxYmM1jNAzGW/ioAP2M/ewB4XBQWUVP7dTQ4L8ojjwxghWDgVOR/oZmDN3REYFJXtz2w98gCwJOqiCkEldjc5L8gjjtdjimDhQuE8g7TjgRZAtOnWLuBpoDkwVqUliRK7mxwW5BHHYDgKu0ywECZlWUZb2dJjZtmFSKgAeJdd72cwHykfXYZfquxucl6QRxxPhw3Bwht5nwSejZfzAuA+4CHgt3h3Jbumyu4mhwV5xPF0BBEsvJF3Mlt0xP2KfQfwJLs7ASjxpnQRuaq1u8l5QR5xRHR+/DwIFvF1cXs1i+FgqkE2+cAItiQZABwwiBP0ZbV2NzksyCOOdwOHYGFN21xgubWYPFYftqnJf+oD3wOtgIeBVfp7wV9Ra3eTw4I84ng3dAgWFrSNa0+RMN2XbO6wwzTeFqALe3UyWboliXK7m5wX5BHHdMw5v0mwSKSdM1IA2A/cDUxIlH8eMJxhZTBwKFFkH+8rt7vJYUEecTwaJgQLU2Edk0LLdQDQ2TR/fvMbRIzEHwXkcLKl6O4m5wV5xOEjS2CAYGEspktSAPiWTRl+Ny4i+s4moCNbksyIvhpMWNHdTQ4L8ojjxbghWBio6p4UAI5vi94DfGxQhP7yEWAo48tQ9imaPoJfVxTd3eSwII84XowUgoWBqqME2Vm+xBYXtuwpvmDzi46AxSmJQQvcXFZ3d5PzgjziuBkAcdMSLOLKIu7ij2ymsNpmhusZYu4FvrGZUFB0dXc3OSzII46gsVCWDcGiTAtPQnlAa2CU/bwPAYMZaF4FjL5Ys5+rlRSq725yXpBHHCvdbT0OwcK6Vk5jprGPQRz4vykBJrMlSWdgi9PS7adTfXeTw4I84tjvfLMUBAszdcTc+4VNEDKcZraKWXm2AuY4zcFmOtV3NzksyCOOzZ5PEJ1gkUAgAbcLgbbAGy5yygEGMOK8CRxzkY+1pCHY3eS8II841vrcUiyCBXvB+Y4lsZxHGsmcZeU7zyDyfeoEZhL6JGBuQu6iEC1pCHY3OSzII47r4VCWQdLDQog9RZmeBqFlbF6wyOCu9cvL2PbHfcCP1tPYixma3U3OC/KIY28EGMdOblj4QwoAxUB7YJhxP1i/sw/ox9DzLvO+ZT2htZih2d3ksCCPONZ6PnGsJIaFb6TQeuF99vXH0cRdkjhGEfPl2Zx9Ai/6HKMw7W5yXpBHnMSDykKMZIWFz6QAsJZNB+ZZ6BOLUZaUnmPkfnUTVWKYdjc5LMgjTlQPOw8mJSz8JwWYu4rHmZ2V887SpdwD9GYMGiPMaXiYdjc5LMgjjm7oOLmQlLBYKei7D7uCj2MWVgftJjONX8ROPEtlp5+5PscofLubnBfkEcd0GFm6mZSwsKSMB5E2s1nALA9yXiTmHKPw7W5yWJBHHPfDjmDhXkM7OXQDnrMT33rcXYic294cGMdevlhPGBUzlLubnBfmHnFSU6OEYEH9ldgYSfabYOFvh09kz/NebwotAN5hk5d+wD4nRYRyd5PDwtwjjh4N+itONA1RGoKFv52ZyWAx3ctC57PvXNsBy2yXEsrdTQ6LnTtxxRXo1w9DhmDGDBQWltNHjwb9lXIJku9HEsDC+48p7A2bXkBPeylsx97OzjHS3AVb9rsT4t1NjRdpaUhNxd13o0cPNG+Op59GfpQBvh4N+iu2OyJcCcIOC+0t6WGZOm0GWylkelylY8CbrKCB5Y9oNi42xLubmZmYNy9CijffRJUqyM7GkiURakyI8r2emhqJEPPXWK1kvBNqWARiT5FwFO1lK5GJCeOJiDCHnWP0iKVzjMK9u/n222jVCtu2oWFDdOkS0XbgQPTtWyayfh6hv1IWOylD4YWFnKTQBll/oKtfw20LO46gBTAlwTlG4d7dHD48MpU45xxcfjneeisi/oABeDbq8Go9GvRX/OozScsJKSxkJgWA2WyB8IdfY+IokMZKND3HKKy7m9Ono0WLCCZSUzFsGErYJs7PP0e2LSZGze/0aNBf8avDJC0njLCQnBRgJ4+1YB+D+TkqvgHuBR4D1scpNXy7mxs2RN561K8f+TtyJHJy8N57EV506IBu3SKBPn1QUFAmhR4N+itlsZMyFDpY5APdArLmtjWABrPn1vKrClt5G0beWHqO0ZexUcK0uzl3Lh55JLKR2aoVfvihXEsXL46sQYYNwze9UOTAK2q5zJLuR+hgAUDIZ+Bej4Qf2LpgrdfF6PI/AgxhRb9c7hyjEOxubtmCd97Btdeidm289BJ2mX+8/zGwRicOXTBVIIywMG2wLDfz2HuK9wKqzvTSc4w2naiA0rubixdHVhbVq6NRo4i1laUpwxHRXwAH1JN+Fkuw8FPt8mUNA9o5/46jfF72f60FOjB/POzDNhV3N3fswLhxuOMOnHFGZAPid7sHuA0Eooyy7CuYdCkIFsF1+SK2HLBvlC2sxoeAFyJ1OPoSzqiIHTvALaMlD6xYgf79cfbZkUXHuHHIc3YIUzrwuTAtkyEjgkVwvVzAvisfEVwFNJc8k5DdAFNqYPevCsBCew9auTI6dsTSpa6lizLKcp1X+DNQHBbHjylfrnInvQnc74nfXVuifNQLi+oiLxV7J0nKC/17UFsNNIw8CthseJNuxCigMizkt6eIEVv/cylbiSzW3/D1Sps2eD8NuU8j704cfAm7tkqEDJP3oAI0ygGGCsgmSbJQFhYhIMVxk+Midg5IWsCD7cTu5g4ceAd5/x+HH8XupQHzwt57UDf6yfZRspu2eJxWTViEgxRa145m71CdbdGJGBwxtpvZ3+FoS+Q1x97pwfDCyXtQETpQHgkVUBAWYSIFgNVsJTI/YU95FUFvu5m1GrndIkuSnGHI3OYTMty+B/VKHsq3TAHVYBEyUmjvIx4FXizrEp9D8W03t+PAG2xJ0glZy73lhZj3oD6rlpTFqQaLUSp892F3JH0M3MO+LrObUER8E9vN7G9wtAWO3o3srz3hheD3oCLUoDxMFFANFiZNUffWJrYSmR1MA8xtN7NW4HBntiR5HZnbxSDDq/egweiXRKUSLOTo7C7A8wHUJGZ3M77h5nbkvBrhxeGuyFrlihfevgcNQL/kKpJgIUd/TwDudui/300D9Lub8XmRib1f4GhzHL0X2bNt88K/96ButJjjJnFSpCVYyNHNO9hKROdmwuvKxd/dzIyPg6zfcPjxyK7ngZHItPYhiUrvQV8J43aY0AFEsBAqp5vMerJTjt3kYD+tye5m3CnGrq3IGRJZkuR2R9ba+EzJzIx8k+bqe1D7DRGQYjvAfHMKyCqkWUgMi1zg3ZCqHrdZ05jXb3OXLXETurhovrsZlxeZmdg7JfIhydHWyJ4bywu134PSd2WmY0lWWITPnsK0GyI3sxksJiWMJyyCpd1NgyXJ7nQc6YC8RjgwGpk7I8gIw3vQ6cAiYfKGLyMpYZGEpNBGVj92kphfo8z67mbcKcauzTg4GIdvw0+34dqLyvzi+lV9D8opDOadlAct8SRL+WCRtKQA8A3b5tziSU/rM7W1u6nnhfYe9J6K+Lk2dt3F7Nb1ZSh35d+BWcfJL5VksEhmUoCdM9gC+MThsJk/P+Lh/scfrSa3u7up8SLOe9DNpecYTbVatLzxNgLvy1u7YGsmEyySnBTaQBjEvPU7GhRDh0L7azG13d1Ns/egR4FX2LToJSDXYvmyRvuvrBULul4ywWIFvegG5rJHLt45QOZD5dgxtG2Lfftw//04ZsFHg/XdTRvvQb9mH7k8BmwwryzdVVIBmWChpICiK32Eedy2PxNeuBCDB0cqM2gQFi5MXCsru5tO3oNuZIcn3QN8lbgOFEMtBQgW8vXXy0D7BIcY6yudloZZzKn/N98gzYLrLfPdTVfvQQ8DL7H50bBy5xjp60xX1FKAYCFffy1kT5odR8T5+WjdOrK7qf297z7kG5yIsXv37ief7HnJJdeefvpVDRo8lZGxPfo1h8jvQaexc4yeAErPMZJPaKqRPQUIFvb08iN2Pjsi4G0bRS1ejAEDyuL3749ffin7yUNLliypWrVWvXr9brrp14YN0+vVG1S5co2pU+dnZsKT70H5OUYBfX3PG04BIQoEBwuDf/qEtEr5TN4AHgAKrbbjtdewYEFZ5B9+wOuvl/3UQseOHTv33HrXXDONT0BSU3HDDd9XqXLuVVflWjofNDZLC78PHt9EYROl14Dg/IxaqChFSaxAQLDQ3pIeTly/JI2Rzh6weLMDvSCFhZETdwqjyJKfj8cfL3cFwPz58//2t39Fk0ILn3lmk/79v7B0Pqi+bCtXStjBX3cDXYFtVhJIEydbmprIUZEgYEH2FAn7vgh4EBieMJ6NCO+8885FF3XTw+Kii/oPGeL94Rkr2K5ta2CejToHHPX54M9/CliB8sX7DgsiRfkOMPz1LtAasGAxYZhD+RszZ84877wmeljUrfvAhAkTysf15td+oD+bMb2lyInEvwAhsEkV15n+woJIYb3nVrHnKmonwnrSuDEPHDhQtWqtm29eHs2L227bWOnUyts2rIibRPzFYuBT9nFtd2Cn+OzF50gfrUdp6iMsiBRRuicOlgAdgH8njmg9xn/+M/H008+59tovmzYtaNas6Prrv6ta9e+vdLlxeZ/q+5dMtJ6P25gZbJHVBrBgPOa2LJfp3wa2uswiPMn9gkU+0I2suW2Omw+BewGh28ALFiy47LLr/qfCKf9T4S/161/87bevAvMPbx69+oU6v4+6u/DQbptVdBo9G+jLpk6jbbz0cVqYi3T7gWEukocrqV+wAHA0XMr50JqN7HHywJHstq+HbPr8fmA+/1tSOGfH9Ha+TjGKgI/YkqQn4BejnHTac0Cxk3ThS+MjLMInng8tegKIsrYSVeCu2cN2THuQk4IHAphi/AK0ZX+tvScWpYCNfH5gfkZsJAhtVIKF3F37GTsi4IDgShrBApgfwBRjN9CTTTE+YsfKC26r6+xKgHdcZxKKDAgWcnfjNrYSEf0FpwkstFmG31OMQmA0a2lf5otU7j5J2toRLKTv+h7AM4IrmRAWwUwxFrKPYh4EMgS3l7ITooA3sMgF/HpzL0QFqTOZwqboQrcArcAimCnGTqA7a++ntK0o3aj0ABZkTyG2l3ezh2eyyEytwyKAKUY+O+wnlZl77hfZasrLpQKiYUGkcNkhcZP3Zf/exr3l6KItWAQzxZjHrN3b0xTVUQd7k8gVLIqKMGECHnkEzZujRw/8uoAsr7zppa/Z5p+4TzYdwCKAKcY29qHq3eyj1RJvhKVc7SjgChYjRkRcM6WlRZDxdPdIeLEHFkR2mhPSuAeY16lPhbXOGSwCmGLkAa8xUA4CjrvGoD+BKuAcFjt2ROjwn/+w6ueiuBt690CXLoG2JsSFDwSeENY8N7AIYIoxmzkx7gCsFaaAw4yS++Rk57BYsCACix07gO3bUflZDHhj6gf7mzdHHjlEcjgSTZPNYf/AbjSNY/mmS1gEMMXYBHRi06vplhvpRcQpwK9e5KtGns5hsWpVBBYnfD3eeivq1Bl57fgHmh2MLEu2+HUCnxoii6jlYfZR2YcisgKEwMLvKcYR9k1XKnMdLvTjOhuaFnhifW+jAoFGdQ6LwkJ07YoOHZCRgaw/jky/4ZW7m5d80Gs1jp+KV60arrmGqCG4Z4ewj9ZFbPWJgkUAU4yvSs8xEjTJst1HL6p/5JrtNp9I4BwWQGQC0blzZH6h/X35X1/lT/4C69djzRqMG0fUcNopBul+YiuRlQZ37VwWCwu/pxgbSs8x+tpOm0XFXQcImt+JqpFv+biCBYCCAvz2W8SR/KZNwJQpOOcc/PprhBfaX6KGwJ48xkwPRHzUJBwWfk8xckvPMXolCNcHyeo+yy0sYp+F3r1xyy1Yu7aMF0SNWI1c/H6N+ZgqcpEDS+oRLPyeYkxlW56dgc1uBbGX/hNAxPzOXqESxBYNi6Ii3HQTunePhQXNNYR09q9sJbLEbV7ewcLvKcZqto/TEvjOrSY20h934zTIRvTQRBUNCwBZWahdG2PGGPKC5hqOh08RO3xId4CQ3fy8hoWvU4wc4H8ZQ9/w8RyjfXYlD0N8D2ABRI7xrl4d8+Yl4AVRw8EQehu4z60rfR9g4esUowSYyLwEdVPtHCMHAyC4JK5gwd+D8EBZQ958E5ddhhUrLPGCqFEmXKLQCvavqDu/2L7BwtcpxvLSc4x+SKQh3XekgFtYmBXapk3kbG++W2E9QO9QTGQtAR4G3B0h5icsfJ1i8HOM3nY7+TLpgaS95SUsDh9G/foYMsQJL2iuYTIkx7BvJY6YxEhwy39Y+DfFKAY+YR5AegCZCXSg27YU8BIWANatwxlnYNo057wgauj7cz1biczV37B6JRBY+DrFSFfnHCOrnRZ8PLew4LsVWiBOg/SWWtbXI/qYtELRJO7o6u1dgLDwb4qRzXyXpgLvS+k0PM6jIvslt7Cw1D4jSy09C6xfSXJqjGf2SDmW5NdHChYW/k0xiphpdirQ27NzjP6rVze0V3yBRUJLLeuM0MdMTmpsZSuRmQ7HpQyw8G+KsRi4n51j5MXX5SOB7Q57QblkvsDCuqWWngXWryQbNZ4EnnU43iSBhX9TjKzSc4w+Fr0k2QukOewF5ZK5hUXiPQsuiS1LLeuM0MdMEmpMZnv+2VxfGwGpYOHTFKMQGMWmY8+KPqC7HyDCb4CN/gsoqitY2K6zA0stPQusXwk3NbIYLKba7gSIc36jTQ1E/dePY9AWMPvXh4ClTnSLn+Z7f79MiV8JP676Cwsg4uTCmaWWdUboY4aVGn2Ap52MEtlmFhw3fpy0ugN4inH2M0HnGJUA/Zz0gnJpfIeFe0stPQusXwkZNb5k8+odtkedtLDwaRcjHxjBpBsACDl0+lVgj+1eUC6B77AQaCTINZoAACAASURBVKllnRH6mOGgxn729dQE26NOclj4tIsxF2jFPidx75xiJ/Cm7V5QLkEQsEA8n1r659mfK6pTYwDQ2faokx8WPk0xtrBzjFoAk1xvUn5vuxeUSxAQLAB4Yanlhi+KUuNbNp3+3d7AUwUWfkwx8oDhTMMXgEP2ZEy22MHBwlNLreShRi7zdv2xvXGrECx8mmLMkuYcI3s96Wvs4GDhj6VWMlDjJeBRe7No5WDhxxRjE9BRgnOMfH387RUWKCzs+tRy8+S7SSv5CuVHNotebaPjVYSFH1OMI8xRSCowBHDhAcBGTygVNWhYAPDZUit81MhjRwSMsjHu1IWFH1OML9n8oiMQ1DlGNnrS16gSwCIoS60wUSMNeMjGVw9Kw8KPKcZ6do7RvcA3vj6NkhcmByyCtdQKATV+YSuRDKuDLQSw8HyKcQgYzFRNs3mOUXgPBpcDFpJYaqlLjUL2CfYbyQULz6cYJcCU0nOMrB/1PTi0+x3SwEIqSy0VqTESaGPVS204ZhYaLDyfYqwCHmG2nnOssXgNMNZaTNViyQQLCS21FKLGMjZnXmRpAIYMFp5PMXKAgUzeN4FjFhQO6WGoksFCWkst+alRzD5zGGZhKMv6iTqfKTgOePjRagkwgX2J86QF11gfA2sMO+Kuu+6aObPMx9nMmTObNGliGFumG5LBQn5LLZmp8T4zQzx+EmeiP6GcWXDEeOgXYxnQjr2onm8q8RG2OWoQZd26dZdcckl+fj6A/Pz8Sy65ZN26dQZx5bosHyxUsdSSkBpr2VR5XuIRFm5YeLuLsY95r0gF3gUKjKUeaLZ/1LNnz7S0iDe+V199tVevXsa5yHVHSlioZaklDzVKgMfN/k3jQy/0sPB2F6MYGFd6jtEuLmr5QDrwefkrUb9ycnLq1KmzYsWKCy64ICfHqY/2qAz9CcoKCxUttWSgxjj2qu9ggsGTJLDwdoqxhJ1o3wYw2lQebtYL7733XqVKld5//32zSJLdkxgW6lpqBUiNzWwlMivBKEseWHg7xdgD9GGC2z/HqLi4OCUlpbi4OEFXyXRbYliEwFIrEGp0A55LMMSSDRYeTjGKgDGMF71te9ZLSZH76dMNIumrK/b0QzdPb1Bp7X7zOpEtp/fqujrqQhLCwtspxiJmEfcAsCRK5URBgkUihRzcl82nluTUyGSwmG4mdNLCwsMpxi7mab052/ssMhOf3yNYcCnEBUJpqeWGOAnnGr3YAVzGPZDMsPBwilHA3qemsner+4zVV/aO9MsQTdmsLNSujTFj4OYZC19aI2rMYKvoTMNRSbDwcIrxY+k5RsvK9P/uu+/KfigbUgQWyWCp5YZlMdR44S3ceRQT44/KuXPn9u9wV5/7/zl79qslJT9o/9Im7X/15p47duz44IMPnn32uY8++igz05i48dVlV3cAT5ae0lCCRx999PiLj4EDB5qkUOKWOrBIHkstIdQ45XWcORlpadhS9nH1vn37br+9ac2aV1x04bP1Lnr+rLOuvvHGa3btmpa0pNAaHv1FyUcfja1cucaFFz5Wv/7LF17YoUqVGp9++pmTJ/kYO0kkFSMajUhJSalevfpJJ500YYL9I16clO1VGqVgkWyWWm6o8f5WXLEdzZ5CtWq45hqNGs2bt65b98lmzYpKj7Muueiifg0bXpfksNCaf3jz6M8eq12pYvXbbttQqg9uvXVN5cpnpaenO3v+Bjw4ICUlpeWZLQ++c/DWW2896aSTXn/9dWdZyZBKNVgkp6WWA2os3Yg7cjFsF0pXKCuqVKl2Sq2mTfP5k5CaimbNimvWvHTBgpHEC2D+TQ2uv+qqidH6pKbiiivG3nlncwfPap8+fVJSUq7957WFqYU4DUdWH6lbt25KSsqIESMc5CZDEtVgkeSWWrao0X0vWuVg3XptV/jDf//7wvPaxzwJqam48IKnBrS9ePPYpvS34il/bdx4X4xEd96ZWa3aWQ6e1ezs7PPOOy+y+rhmAq7EiCGR9cgll1ySl6eq4z0FYREan1q2nnwHkcdvx22HMWuzBovPhg+vW+f+mCchNRV1L+j4ap/2exeNpb9Vq1S/886dMRLdfvumWrXOdwALAEf2H7n1b7ee9P9Oat+8fWQ90rJlYWGhs6xkSKUmLELmU8sBCKwkWbEBjQ7hxSwNFpu+/77yaTUaNz4Q/TA0aXKkatXzli2Lessnw6gMqA7NmrX+xz9GRuuTmorLLnu1VauHHNboTRxpduTSCy5NSUlpeHZDpUkBQFlYkKWWFV70ycbdB7H2xErkqXaPnv23uxo33q89D3fddejcc1s/9NBjDp+E0CXbuHFj5co1rrtuFufFtdd+VaVKjS1Rb5RsNHoOs3aZgOzs7Ntvvz3v8zzD71NtZBpkVGVhEW6fWlZAYCXOxK2RlcgXW7TJRf6qVT07dDytQqXzz76rTp17KlWq0anTk0eO0NlbZU/gwoULa9euU7v2NWed26pGzctPPbNq50/sn1IPYAvzWjYg6ljJQuD5soJUDKkMC7LUSsiL1RvQ5BCe363BIvLfjIydp502Y8KEadOmbd26VcUh63Wd8/Lyfl7880kdThr//fgZG2dUG1tt1f5V9go9CnQGHgZi/Npst5eNbLEVhwVZaiXkxfN70PQQVm84wYvhw9GsmX4U8on3PfegVy/8/rs+ShJdKSwuPHnMyenZ6enZ6QOXDLxq6lWFxXY2JtOYCyKbhJFfX/VhQZZa5ryYviWyEpm09QQs7rwT48frx2Vq6olrx45h8mR07aqPEqorGzdiwADcdx/efhu7d8c2LRoW6dnp/5rxryFLh8RGMvr9DduqmGJ0W+HroYAFWWqZ8GLNejQ/iGf2aGsQVKqEg3G87nFYHH/RlJuLNm0UHtMJq751K9q3x6JFyMvDzp3o3x8x33nFwGLm1plWFyMbgXuZG9SShLVQL0IoYEGWWiawWL8eg7Mi71BXbIDBGgQAh0VBAaZOjfwN8Z9XXsG335a1b+dOjBxZ9hNADCysLkYOAx2BR4FD5XILzY+wwIIstUx4MXNzZCUyfhsM1iAaLPi2xXEb5y++CM0Ij9OQdu2wy8grN4uuh4WlxchQ4B5gfZwSw3EpRLAgSy0jXqxbj5Y56JJptAaJnlkUFmLJEjz8cDiGd/xWtGgBc0PKuLBIsBjRfIh8Gb/EcFwNFyzIUsuIFy/vwqUb0Li10ajlyxAAx45Fdv5C/Ofhh7EvypNVSQkOlV84xIWF2WJkLXv9MdSyZissx5QpYrhgQZZaRrD4/g9U/xl95xqNPQ4Lbc9i8GCjiGG4/uqr5fYsVq6MfftjBIv4i5FDbJ+iI2Dduu0DJVcroYMFWWrF5UVGBip8gD6GR4DzDYvj70EGDYrzNjEMkChtw6ZNaNcOv/6K/Hxs3IjOnTFnTuk99n8TWMQuRkrYu4+WwKZyOST4kQu8mCCKhLfDCAuy1NLzYvhwXJGGu4Go6beEw9G3KmVkoGdPtGyJxx/H11/HFmsCi9jFyGRmVZHoVKfYAo6/cXne9KjUOAmCvxRSWJClVgwv7rwTI6ciFQj1Dpyo58kcFmWLkZXM0abpMYWGVfoFUO39dHhhQZZanBcZGSfeg/QEehuOXrrBFUgIi5lbZ57/7vkH2h5AF8CxL5u+vEA1AuGFBVlqcVhwW6xp7PwhUxMDNYatx7VMCIv0PenzH5v//Q3fF/5h55uRmGq/DSj1KV+oYUGWWhovuC1WNoPFpJgxSz9jFUgIiz9G/5HTKKf7i91tfDMSWwiwHximvyrvlbDDgiy1+BpEG4T92JEW8g5IKWpmDos1P6w50PjAtqHbYt+MOKi7UpaySQCLJLfU4msQbShr30SWnSXiYICHP4kJLJatX7av9b7dj+/O2JkR+2Yk7MIkASyS3FKLr0G0oZzDbA0/Cfu4dtc+I1hkZGXs6r5r/937l69Yrnm7KHsz4q5EJVInByyS1lIrZg2iDclB7ONIJYZnQJU0gsXmtzbnNMpZ99U6Tor07HQBi5GAmmm32KSBRXJaasWsQbTRMZfZEYX340i7z4A+flxYrP1u7YHGB7a+ujWaFM69aelLlf5KMsEiCS21YtYg2nA8wnzJvi/92AyugnpYLFu7bF/LfVmdszIyI1sV+r/2vGkF1zQ3JScZLJLKUivuGkQbLC8D7aMcT7sZQWFMGwOLjF0ZWV2z9t2zb/nqsq2KGF4kw2IkyWCRVJZacdcg2rO9kK1ElofxQRfRphhYbHl9y4HGB9bOWhsDiJifTlz78tqq4IYv+WCRPJZacdcg2ujMB9oAb/OhSoFyCkTDYt0363Ia5WwZsSUGDXF/Ol+MDGc2WuVqId2PpIRFMlhqmaxBtEH4BvAA4MJYWbqxLK5CHBbLVy3f32J/1pNZGVnxtypikOF8MbIFeEdcA7zJKVlhEXpLLZM1iDaS0tlK5BdvhpXiuWqwyNiZsbvT7n0t9y1bvywGCiY/nS9GpP+uLFlhEXpLLZM1iPYkFwEPAs4+r1acBQmrr8Fi67CtBxofWPP9GhM0xL3lcDEyBfg1YdWCjJDEsAixpVbCNYg25N4FWgOG3rOCHJfBll1YXHh7n9tzGuVsfmdzXByYX3S4GCkABgTb7gSlJzcswmqplXANoo2KVWwlsiDBEEnC24VbCidfPXnX07vSd8cxqTAnhXbX4WLkRSBXXr2THhahtNRKuAbRBmQJ0AH4t7yjM5iaHUNx1+LxN4z/beNvVrhgFMfJYmQd8GEwjbZSKsECCJmllsU1iDY6PmTH7R22MlSSJs4bKGlecsWgK4woYPG6w8XIIHl1Jliwvlm3DmecgWnTTpwezH1MqRiwuAbRxuRGthIp79ta3tHqQ82+iwhS9J8ifoq6RTTEjeZwMeJDMx0VQbAolW3KFJxzTsQ/vIqAiK6zxTVIabvxhOz7arymngc2s69m/heFRYVCYBGyD9gJFlEjsHdv3HIL1q5VmBe21iBa0z9jLqoPROmQnMGjQGfgESAnzsHIcScOVi46XIxI2QUEi6huCYGllq01iNb0bWwl8lWUDskZfIW5BVodaTy34LSCg4RxQrMYIViUfzKyslC7NsaMUXVyYXcNorW+B/BMeR2S7dfXjJilB3mIhUVoFiMEC91jsXAhqlfHvHnq8cLBGkRr/RTm9Xu3TookubCRvRJ6qeybfeGwCMdihGAR74F4801cdhlWrFCMFw7WIFrrdzNYTI4nReivHQYeBx4rZw0lHBbhcO1LsDB4Gtq0QevWisHC2RpEE6Av0N1AihBfLmE2affEnmnuBSxsL0amS/dNMMHC4FFQzlLL8RpEE0BbtG8zUCOsl6ezrQrd+a8ewcLeYmQRMEMu3QkWxv2hlqWW4zWIJsAB9i7gU2M1wndnLWtyvDPBPIKF7cWIZB+tEyxMHwKFLLXcrEE0DQYiYqCVJH8Osu9iOgFH4jTYO1jYW4yMBLbHqV5QlwgWiZRXwlLL5RpE02AOm5NvTCRICO4fd3g5iBlrborfGE9hYWMxshdIi1/DQK4SLBLJroSllss1iKbBYfYGUeKvHhN1leX7nzMszjaM7yks7C1G+pW90DWsrl83CBYWlJbfUsv9GkSTYQibnKvgadpCtxlEWcHM218zuMsuew0LG4uR74HvzKrq5z2ChTW1ZbbUErIG0WT4if2Tu9KaJirG2s8OTOkK5JnV3gdYWF2MlAD9zKrq5z2ChWW1pbXUErIG0WQ4xhztSe9m2nKflY9YAvRnDUz0htgHWNhYjKwp34rgfhEs7Ggvp6WWqDWIpsRrzJFvkR1ZVIn7KZs3zU1cXX9gYWMxkrjKfsQgWNhRWUJLLYFrEE2JX9kTtcSOLErEzWAm7W9ZqqtvsLC6GLFUa88jESxsSiybpZbANYimRBE7fOh1m7JIHj0beIjZs+dbqqhvsLCxGLFUcW8jESzs6yuVpZbYNYgmxtvAfYC158q+fL6nKAL6suMad1ot2k9YKLQYIVhYHUDl4kliqSV8DaI1cgVbiSws12KFf3zEmvOTjRb4DAtVFiMECxtjqCyqJJZawtcgWgtLgIeBoWXNVTj0C9uqGG2vBT7DQpXFCMHC3jAqiy2DpZYXaxCthWOYNXS87ybKFJA/tBtoC/Sy/a23/7CwtBgJ2hKfYOFiyAdrqeXRGkTTY73Vt4wu5PM4aSHDRFvAvgewQGCReDFy3Eo9w2PRTLMnWJjKk/BmgJZaHq1BeJM7sq+t+E/lAqPZAmSxk3oHAovEi5F8YKCT5ohKQ7BwrWRQllrerUE0ScYzdw85rvUJJIOFbGb0kcOyg4JF4sXI4Pjf1Dtsp81kBAubgumjB2Kp5ekaRGvjVva8zdQ3WPorO9mL0r6AUzvUAGGRYDGyBhgbmP4ECxHS+2+p5fUaRFPlSeBZEfr4mUc+M756EMh2XmqAsEi8GAnOfRbBwvmQKpfSZ0str9cgWtsms2W/i6eunET+/HiL1dndRmCwsEiwGPkYCOjTMoKFuCHsm6WWD2sQTZUs9uCVHr0jTinPcprHlk6uPYkGDguzxcgRYLBnAppmTLAwlcfWTd8stfxZg2ht7wM8bUuF4CJvY5+f9weK3dYhcFgkWIx85raBztITLJzpZpDKH0stf9YgWhO/ZP9W7zBorzyX84CuzLHNfgF1kgEWCRYjAlppOwuChW3JEiTw2lLLtzWI1s79zAndhASNDv72a6yeK8RURBJYmC1GxDTUXi4EC3t6WYrtqaWWn2sQrbUDgM6W2h1YpNls+jNRWPmSwCLBYkRYc61mRLCwqpS9eN5Zavm5BtHa/C17FH+3J4B/sf9gn7EMEukFWx5YSLUYIVh4M6o9stTyeQ2iaZML3AN87I1QLnM9wg5G6gAcdJlRueRSwUKexQjBotwoEfnDC0st/9cgmiIvAY+K/KdbmM7DmE36WmH5aRlJBQt5FiMEC8HjrFx2wi21/F+DaO35ka1EVpdrXPA/vmK1mia+IrLBQpLFCMFC/FArl6NAS61A1iBaY/KYCcOoci0L+McGtjh6yZP5joSwiL8Y+QDI9K8fCBYeay3QUiuoNYimUBrzeev00yzBKucCj7G/uYIz1rKTEBbxFyN7gOGeKBA3U4JFXFmEXhRlqRXUGkQT4xc253f3zYUYWUuAl9ixrBvE5KfPRU5YxF+M+HgYKsFCP1Q8uOLeUivANYimRyFzUfeGB+LYzXIqw9bXdpPZiC8tLOIsRr4FLBybZKPxxlEJFsbaiL3j0lIr2DWIJsVI5ici2CMC1rDXH8PE9k1sbtLCIs5ipNi/w1AJFrEDxcPfbiy1gl2DaKIsY/+kL/JQoQRZ57BD3p/w3FuUzLCIsxh5BdibQDkhtwkWQmS0loljS63A1yBa+4rZl1oe/6tuKGUJ8L/MWPMPwyiibkgOi9jFyHbA2rGMLvUhWLgU0GZyZ5ZaMqxBtIa+zx7XozZbLST6RDav+VZIXgkykRwWcRYj/RK0SMhtgoUQGe1k4sBSS4Y1iNbEteyJnWenvULirmAflfp1Aqv8sIhdjPjySptgIWQs28zElqWWJGsQrYklwOO+e2raz5Y/XYE8mzo7ja4ELGIXI04baz0dwcK6VuJi2rLUkmcNogkwjr2PEPrhlpmyxUB/Zj+6zSyW2HtKwCLOYkSsCrrcCBY6Sfy5YN1SS541iKbMZrYSmeWPTMB4VtwPfhXHylEFFrGLEY9FIlh4LLBJ9lYstaRag/C2dAOe4z+8DGQwj8Fve1lEvLwVgoWfixGCRbzB4tu1hJZasq1BNGUmsmfY63f72cCDQA/AdzMwhWDh52KEYOEbGAwKMrfUkm0NojUik8FiukGLhFwuAp5hBqM+flXJK64WLHxbjBAs+AgJKGBiqSXnGkTTqRfQ00vFPmRbFQu9LMI4b+VgUbYYmQt4ZgVDsDAeMr7dMbLUknMNoskygz3MHv2zv5jNXN7zrQNiC1IOFnwxUrS8KLIl7M0fgoU3utrNNa6llpxrEK1pe9nzLM6hdplgWcD9QG+gsOyazyEVYVG2GPHsMFSChc/j0Li4KEutgxkZ+YsXo1IlHPTNnsG4YkZ3+rNzfYzuOrtewFY3bYHdztKLSaUoLLTFyM6RO7Ee+/fvLywUjFuChZjhJSAXZqn1WePGf699wSl/qfSXP59yZdXaS5YsEZCzR1lop3WI/axrNJuw/OJRja1mqygstMXIBQ/XrVX5/FNPPf0vf6l44413rFkj7BhlgoXVAeRDvAE9n6lRsW6DBotTU9G0acFVV02qXLnWd99950PRToo4xEw5xzpJGj/NArYPIsGZA+rC4u4H7zv9zCtvuWUlG0J5V1zxYeXKZ6anp8cX3OZVgoVNwTyLvmrVqsqVz2rUaE9qKvjfG2+cX7Pm3/Pzfbc0sNjMwcwRZonF2KbRdgD3Ac8CvnwTZVoVKAqL9798//Sq5zdpcpiPn9RUXH315Asv/Ed0exctQosWkTF2771YujT6ToIwwSKBQL7dHj78tYsu6hXdzVq4du2rRf3LIL4tP7C5gPtjO/KBp5hDYK8NvaxJoCgsHur6yMUXD9MPodNPP3vbthOf1ixahFatsIh5MFqwAPfdh5UrrYkCECysKuV1vC5dul966Qh9T9ep03Lq1Klel+4w/zygFeD+HedItlVh5185hxW2lkxRWNzc+K6rrpqoH0Jnn93gp59+0preogV+/rlMhQULYH1wESzKhAs2NGbMmLp1O+h6uqTaaXXWD1+Pw8HWzrj0YUA7oNg4QsI7c9n05NOE8fyLoCgsuvTrWvfCvjFDqGnTgr/+teqBAwc0+VJTnctIsHCundiUu3fvrlq1VsOG6dGd/Y9/vHXNNTeVrCjBUOaX9TOxZYrIbRF71Jc5zWorm5s878lZQU7rpOqeRY8ZPU7+62m33fZ79BC6+OKBTZrcy6WIhgWPxu+aBwgW5vr4eveLL76sXLnGxRcPbdgw44Yb5tWt26VWrXN//z3q/PKNvtbHUmEF7AuOEZbixkbKY5Ya7YET/+zF3g/qt3Izi1nbZ9385c2XT7n8xbf+XalSjUsvHXHzzb9df/3sOnUePO+8+rt3l1mtRMNCk1d/xUh2goWRMsFc37Rp0+OPd61X76prr731uecGHjp0KJh62Cr1TWZzWWArDYv8GnOWZ3mDzX4BDlOoBYvB6YOrjas2aMmgguJIHyxfvrxdu8cvvPCfDRo0Gjx4SF5eOf9iMXsW2psRizIRLCwKJXe0H4BPEdi+xlK2EllsU6JZLNUkm6l8ia4KLPiEYtleq+tA7W2Itsf5889lb0as6EqwsKKSCnFW4sS+hv/UKGJvPdPsqLSJeQl/Qa6tCt4AJWARM6HglU8Y4HYWLVqceIeaMIkWgWBhUSh1ogVCjdFsn7LchNdYsSNAJ3ZckKxrLMlh4WBCYdwZNu4QLGyIpVjUlcAcv6q8mq0p5lsr7mVmJ+7elMtaaQ5iyQwLxxMKBzrEJCFYxAgS5E/+Kis1NWKQG208E2S1rJRdAjwKvGgh6pcMK5562bJQC/MocsIiqAkF14pgwaUIPhD9Eit6I0p8zeZ5sBv6MXAPYL6yWM/iDBHfILE5SgiLACcUXFuCBZci+EA0LIDI5lOLFt7Uyot9jU1syjDbuMKH2FdnHT3glHGZzu5IBYvAJxRcQ4IFlyL4QAwsgMingd7+EUuNLsDzBvUtYYuUewEJ7cp0VZYHFjJMKLg8BAsuRfABPRr0V7yqpUaNTe6yn8CMrPbFy2QKm3fMjHdLvmsywEKeCQXvH4IFlyL4gB4N+ivB19KkBjsYEb7UxVjFXn/YMsTQ5eHnhcBhIdWEgitPsOBSBB+IQYOHexa22nrMzi5DT+ZrNzr/HOARoLOHLuqjSxMSDhAWEk4ouKQECy5F8IFoWNg1xfWw9jl2bEOnMc8Uu0qrUwIMZMaaW0qvqPD/oGAh54SC9xjBgksRfCDGzkJzZxR8tXgNrOyGZjNYTMIJ10wT2MLEN9swXlV3Af9hIfOEgmtJsOBSUMCyAho1hhrE74crq19ZoUKFDV9uwN3AGwbRJL7sMywkn1DwjiJYcCkoIEaBp5o/lZKS8ueT/1yvcr1dj+7CMTHZ+pmLb7BQYkLBlSdYcCkoIECBJ554IiUlpc8FfRbeuLDiyRXrXVBv/fr1AvL1Nwt/YKHKhIJrT7DgUlDArQLXXXddSkpKl9QuuBiojoWvLfzzn/9coUKFHTt2uM3a3/Rew0KtCQXXnmDBpaCAWwVGjRpVoUKFevXq7fp6F/riqRsi65HrL7g+MK88ThvkKSyUm1BwFQkWXAoKCFBg4cKFFStWrFev3mOPPRZZj/TpA/4O5QcB+fuThUewUHRCwTUnWHApKCBGgYULF1aoUCElJaV79+7lcpT2NINytYz88AIW6k4ouDwECy4FBYQpMGrUqAYNGgjLzveMxMJC9QkFl59gwaWgQEAKvBqot+F4jRYIixBMKLhCBAsuBQWCU4Dva/jvbTheo4XAIjQTCq4QwYJLQQEJFIimxtHA6uMeFmGaUPBuIFhwKSggkwIrgbh+MXypoxtYhG9CwSUnWHApKOBWgdatW8+eXeZXb968eU2bNnWbaRDpHcMilBMK3gMECy4FBdwqsGfPnptuuqmg4MRBhrfeeuuGDRvcZhqTfqcfu6EOYBHiCQXvAYIFl4ICAhSYNGlSWlrEJdaHH374zDPPCMhRn0X0voY3tht2YRHuCQXvAYIFl4ICYhRo27Zt165da9Wq5fmpzp5RwzoskmFCwYcFwYJLQQExCqxatSolJaV///5isrOSy0pgtJV4VuNYhEWSTCi4agQLLgUFxCjQtWvXgQMH/v3vf/d8ZiGmvnFySQiLpJpQcIEIFlwKCghQYNKkSWPHjgXw+eefe7VnYauaG+x4Gy7N2RwWyTahKFUFBAsuBQXcKrBnz5477rijuLhYy6hBgwbiTzZpqwAAAjJJREFU34bYreMGO96GSzM3gkVyTihKVSFYcCUo4FqBVq1affvttzwbuews7OyGxoVF0k4oeIfSzIJLQYHkUECjxneGjS0owH9/Lrrw2X4T5vz+a1ZGenZ6kk8ouFIECy4FBUgB7NqFbt0iR8xqfzt2Pfr83Derjas2aMmgguITxmZJKxPBImm7nhoeR4G+z+Chh7Ako+h/3jtt9Kz0Zq0P3tnpl2V7l8WJmnyXCBbJ1+fUYgMFsrMjE4qZnVA0vqjS25WqjavW5a3ZqanIyTFIkGSXCRZJ1uHUXGMFNm6MwOLXX1GysqTVy62W7V323/9GrmyJOnuRr1C0gHFmIbxDsAhhp1KTnClQUIDWrTF0KEpKIhmUlODFF9GmDYqKyvKLPo+27GpyhAgWydHP1EprCnz9dWQq0bs3xoxBr16RcNQ395EsCBbWhKRYpEASKPDTT+jZE/ffH0GG/mxqgkUSDAFqIikgQoHoPQsR+amUBy1DVOotqmvgCtDMIvAuoAqQAmooQLBQo5+olqRA4AoQLALvAqoAKaCGAgQLNfqJakkKkAIBKkAbnAGKT0WTAiopQLBQqbeorqRAgAoQLAIUn4omBVRSgGChUm9RXUmBABUgWAQoPhVNCqikAMFCpd6iupICASpAsAhQfCqaFFBJAYKFSr1FdSUFAlSAYBGg+FQ0KaCSAgQLlXqL6koKBKgAwSJA8aloUkAlBQgWKvUW1ZUUCFABgkWA4lPRpIBKCvwfHPHWuLYpEskAAAAASUVORK5CYII=[/img][br][br][/*][*][left][b]A terv:[br][/b]Legyen a [i]HAJ∢=BAC∢= α ,[/i] [i]EBD∢=CBA∢=β [/i]és[i] [/i][i]FCG∢=ACB∢=γ [/i], és legyenek [i]P, Q, R, S[/i] rendre a [i]DC, CA, AE[/i] és[i] CH [/i] szakaszok felezőpontjai! [br][br]Lépésenként megmutatjuk, hogy a [i]PQRΔ , [/i]a[i] PSZΔ [/i],végül az XYZΔ hasonló a négy adott háromszöghöz.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAT8AAAFgCAIAAABCHOneAAAgAElEQVR4Ae2dB5zUxNvHV4pynFJVwP6KWEBAVBCw/REEFU+Bo0kTpEhTBEQQkKooTaoIKogU6R2lSa/SQarcUY/rBTjg+v1eM7mdy2aTbJJNstnd2Y8fmUwmk5ln5nvzZOaZZxxgPyYBJgH/lIDDP4vNSs0kwCQARi/rBEwC/ioBRq+/tpyB5Y6MjPz00z61atV7660mkydPycrKMjBzlpV5EmD0midb/8h56dJlxYuXeeaZEbVq/VW9+vJHH32vYsXnExMT/aP0wV1KRm9Qt//ly5dLlCjz+uvHw8JA/3v66X6NG7cMarn4SeUZvX7SUOYUc/ToMU8+2YtyywcaNswIDS2VnJxszjtZroZJgNFrmCj9MaMmTVo///w8Eb1hYXjkkde3b98uV6OwMLk7LN5SCTB6LRW33V7Wt2//ihW/c6e3dOnyERERcqVl9MpJxuJ4Rq/FArfX67Zs2XLvvU+9885tIcAvvbTu4YcrKBSU0asgHCtvMXqtlLYd39WqYYeHH36zbt0LPMAvvrikePGyO3fuVCgro1dBOFbeYvRaKW37vWsOchbkfPfd2JCQe0NCHrjrrnuKFKmxb98B5YIyepXlY9ldRq9lorbfi+YAC/NKFR6Ob7+NPncutXZtLF3qoaiMXg8Csuo2o9cqSdvtPQJ0ATz2GHbtQnQ0pk/HG29IlLVjR9y8ycVnZSE8XCIBi7JeAoxe62Vugze6opuYiGLFcPUqR++lSyhTBmfOiAv5xRdYsgS3b2PNGnz+ufguu/aJBBi9PhG7T1/qii6AjRvx8sscuvx/vXrhs8/EJTx/nosMD+f+f/68+C679okEGL0+EbvvXnoo/1uXFuLbb9G1az69Bw6gdGlumGU/m0uA0WvzBrKieOHhmDYtn97oaLz1FmbOtOLV7B3eSIDR6430AuRZOmVFlef58/HCCwFSuwCuBqM3gBtXVdWEU1aU3qgobhZ6/35VObBEvpIAo9dXkrfLe0VTVhTgwYPRvr1dCsnKISkBRq+kWIIoUjRlRek9cQIlSoBtE7RzV2D02rl1vC7b78B1D5m4T1lRgJs1w/ffe3ic3fahBBi9PhS+ya92W9eVfJ/7lBWld/VqVKiA3FzJ51ik7yXA6PV9G5hSAnXoSk5ZUXqjo1G5MjZtMqWALFPvJcDo9V6G9stBHbruVlZCbvnwmDFo3Nh+FWQlIhJg9AZcR1CNLgC5KSuK8blzKFUKUVEBJ6WAqBCjNyCakVZCC7oAZ7cssrKi3NLARx9h6FD6AhawkQQYvTZqDG+LkgX8oS0PhSkrSu/WrXjgAW5jIPvZTQKMXru1iHXl8ThlRQFWs2XfunKzNzklwOh1SiL4/pWzsqLQ0oDclv3gk5m9aszotVd7WFkaj1NWlF65LftWlpa9y10CjF53mQRLjJopKwqw5Jb9YJGUXevJ6LVry6gpl3dWUGqmrCi9bMu+mgaxOA2j12KBG/e6OcBG/bmpn7KiALMt+/rFbc6TjF5z5Gp2rhrXdd2Lo37KitLLtuy7i9G3MYxe38pf19u9RleNlRWFlgbYln1drWXiQ4xeE4VrStZGoKvSyopySwNsy74pbao3U0avXsn55DmD0BW6X6dkqgmwLfs+aXa5lzJ65SRjv/i5Es5c9ZVSx5QVZZtt2dcnczOeYvSaIVVz8kwwLFsdU1aUXrZl37Bm8DojRq/XIvTDDNRbWVFohQG2Zd8mbc7otUlDWFoMTVZWQm75MNuyb2lryb+M0Ssvm8C9o8nKyp1etmXfJl2D0WuThrCuGN5MWVGS2ZZ96xpM/k2MXnnZ+PbOCbNe782UFaWXbdk3q3m05Mvo1SIty9Iat67rXmQvp6wowGzLvrtsLY5h9FoscBWvMxNd3VZWFFoaYFv2VbSluUkYvebKV3PuJqOr28qKQksDbMu+5sY1+gFGr9ES9SY/89E1ZMqKAsy27HvT2t4/y+j1XoYG5WA+umrcr1My1QTYln2D2l5nNoxenYIz+LGDhtkwKxfMqCkryjbbsq8scFPvMnpNFa/tMvfSyopCSwNsy74P25jR60Ph++DVXlpZUWhpgG3Z90ErOl/J6HVKIgj+NXbKigLMtuz7qu8wen0leR+81xArKwotDbAt+z5oS/JKRq+vJO+D9xo+ZUUBZlv2fdCcAKPXF2L/Hbjug/caPmVF6WVb9n3QnIxeHwjdknVdyXoZPmVF6Y2OBtuyLylzUyPZ2GuqeN0y9x26Jk1ZUYDZln23xjY9gtFruojzX+A7dA23sqLQ0gDbsp/f0FaFGL1WSdqn6Opzv07JVBlgW/at6kx572H0WiJwX6Nr4MZABZLZln1LOlP+Sxi9+bIwK5QFrDUrb/X5mjplRZFmW/bVt4j3KRm93svQD3Iwe8qK0su27FvZGxi9VkrbZ+8yycqKQksDbMu+lW3M6LVS2j57l3lWVpRbGmBb9i1rZkavZaL25YvMs7Ki0NIA27JvWUszek0Qda4JeXqXpTVTVhRgtmXfu+ZS+zSjV62k1KabA2xUm9aadJZNWVF62ZZ9a1qW0WuonG2wruteH8umrCi9bMu+eyuYEcPoNU6qtkTXGisryi0NsC37xnUs2ZwYvbKi0XbDruhaY2VFoaUBtmVfW//RlZrRq0tsoodsjK6B7tcpmSoDbMu+qJsYfsno9Vqkcy1y5qqvoNZPWVG22ZZ9fU2m/ilGr3pZyaRMkIm3R7T1U1aUXrZl3+wuwOg1W8I+zt9KKysht3yYbdk3tfkZvaaK1/eZW2ll5U4v27Jvag9g9JoqXt9nbrGVlTvAbMu+eZ0geOl1uP4aNWpknpR9lbMPp6woxmzLvnmtH7z0UpkmJCQ888wzV69epTFKgRNKN+12z7dTVhRgtmXfpI7B6EV4ePj8+fNVydfe67ruVfDtlBWll23Zd28aQ2KCnd558+aFh4erEqW/oesrKysKLQ2wLfuqOpj2REFNb3R09NNPP52QoGLF1g/R9aGVFeWWBtiWfe1sen4iqOl95513VqxYISmk1atXlyxZ8uTJk9xd/0TXDlNWlF62ZV+ym3kZGbz0/vzzz+3atZMU38mTJ0uWLHnHHXdUqFAhbmocFkqmsnukTaasKMBsy77hPSZI6b148WLFihWvXbvmLtCTJ0+WKVPmgQcemDt3bmhIaKWHKsXFxbkns3+MTaasKL1sy77hfSZI6W3YsKHrci93BWD16tV33nln2bJlT286G1ETmxduCwkJCQ0NzVOhDRe/mRn61sqKQksDbMu+4a0dpPTKyXHy5MkFChSoUKFC9Jq4+MJYVfpksdCShQoV2rjRZt5u5CogiPe5lRXllgbYln1B+xgQZPSKhbhly5bQ0NBKlSote27nvQXK3FfwgWlvnoqLFiez+bWtpqwovWzLvrHdhtErIc9t2ziFuVCBQqULlj3Q8+zVF7CmIpbNQEaGRGJ7RtltyooCzLbsG9hhGL3Swpw0aVLhwoUXVNi48mNgJ9Ib4UQ1jGiEv/+WTm+3WLtNWVF62ZZ9A7sKo1cgzN+BG/mXGRkZmV2wqiLi44GrwKe4/j/8Wg/DhyLa9oq03aasKL1sy35+D/M6xOh1ilDSJGMRLlfD7HEkTQYwBbnv4mxTdGmGOXOQnu581n7/2nDKigLMtuwb1V8YvUSSkugCiEHm2/j+NaSkOAW+GWiGjJaY0w8ffYRdu5zxdvrXnlNWlF62Zd+ozsLo9WQI2RfH6mL2bIHALwHdgfdxZTx6fYpBg3D5suCuDYK2nbKiALMt+4Z0k6CnV27UpdJdhYwG6NEYN2/SKCANGA+EIXcI1i9GmzaYNQu3bwsS+DRo2ykrSi/bsm9IBwluej2iCyCJG2bXfYiF7tbO64FwoANu7MekSWjfHlu3GtIo3mZi5ykrCjDbsu9tMwNBTG8WsFadAAfi5ofcAJuW5pY+EugCNAJW4OxZ9O6NAQNw4YJbMmsj7DxlRellW/a97xRBTK964a3nlOQZ/bFypdQzt4DvuAT4GrmpWL8ebdtixgxXTVvqOZPibD5lRellW/a97wCMXhUyvAE0RvxYTjfOzJRJv4ZLg07AOdy4gWnT0K4dNm1CruVn+dp/yooCzLbsy3QmtdGMXnWSGgF0xPBh3NAq+/uXS4MmeQp5RAT69cPnn+PcOdknzLhh/ykrSi/bsu9lB2D0qhPgVk43jlyLzp2RnS3/SCowkmjRowEyBb15MzcIT53KDcjW/PxiyooCzLbse9Mrgoleb5TYNKApMB0DB3qaWM4FlpF5rK4Amb66dQs//cRNev35pxWKtF9MWVF62ZZ9Rq8KCcwBNqlIppBkNNAWRw6hRw8VEJ4E2pP1JOe+4IsX8eWX+OwznD6t8A5vb/nLlBWll23Z96bJg2PsVbOu61GKe4lKfAR9+mDvXo+pgWvAEPLIBMBpEb19Ozp0wMSJkPLJoyJPT0n8aMqKAsy27HtqVdn7QUCvIegCyARaApM4dPv0kRWoy41ccrTv+0APwGlNmZaGX3/lFOnVqxU/oV0yUnvhR1NWlF62ZV9t67qlC3R6jUKXF9wkDuDcDE55PnLETZZyEcc4lRvNAIElVlQUvvoKPXvihKFHq/jXlBUFmG3Zl+s7yvEBTa+x6AI4QjThvdzE1cCByoJ1vZsMDCTPTgUEDjp270bHjhg3DklJrun1XvnXlBWll23Z19fggUvvXKK16pOK3FM5ZBQdzWm8nTtrnH/KIZuZ3gN6AYLN/enpmDcPrVtj2TJvFWm/m7Ki9LIt+3I9Tjk+cOlVcbyJsmik704nS0dpnNnG8OHSSZRiDwKtgBbAbpdUMTFcbt264ehRl3hNF/44ZUUBZlv2NbU1nzhw6dUhDDWPnCIK8FbOZLJDB0RGqnnGNU0C0I9k8hPgavixfz83pH/7LfHF4/qQmit/nLKi9LIt+2qaWJSG0SsSiKfLXGIOOYJLtnIlRo/2lF7yfjYwkwDcF3A9pyEzk9uK2Lo19/+sLMmHZSP9dMqKAsy27Ms2rcwNRq+MYBSiZ5MNCTe4DYNt2iAqSiGp4q29ZAmqFbBfnCwuDqNGoUsXHDggvqVw7adTVpRetmVfoXElbzF6JcWiGBlJhk2yXWHhQm5fvv5fLNAbeA/4VaxFczPcR9C1K0aOREyM5zf49ZQVBZht2ffc0oIUgUKvoaumAvnIBLuTFSBwm3hbtdL5mZqXdSbwI/lz0B9IFL8uO5ubi27dGvPne/AF79dTVpRetmVf3AMUrwOCXsPXdRVFxt1cwLnL4ZzmgHNYN326xwc8JdgBNAfakCVlt7SJiRg7llsZ3rPH7Z4zwq+nrCi9Hrfsh4U5K+z81z3GeSfw//V/eq1HF8Q5exiwiusfKSnc8JvvMlZ3n4kCPiFa9HxAajvUP/9wtllDhkh/afv7lBUFWHnLvjur7jG6W8DvHvRzen2CLt/IvYG+ec09fbqry1jdvSCDs6PmnOwMBqgHaUFu2dlYtYqbKps9W+xky9+nrCi9Bw6gTBns3MkdOuO+KdqdVfcYgcACPOjP9PoQXXBu6LjZJjKfFB/PDb8uLmO96TabiUFIO+Af6VxSUjBhArfavGNHXoLAmLLiAV6xAmFhef81a8Z5FxL+3Fl1jxGmD+yw39LrW3QBJBB6F+V1j0mTpFzG6u47F4FuZIv/EmktGuDsNHv14sytL11CYExZRUdz422jRujUCTVrch6Fhg/H++9zzjrpj4ItDNC7wRbwT3oPmmDDrKPlB5Ctf+TBqChOoZVwGasjW/6RNGAc0aKHuZyNJswvJ4fz19GmDZo04Xo8VT79NzBxIpo3R0QEHn2UO2UmPZ2r3Q8/5FfafaR1j8lPHegh/6TXJq3yJ6HrYl5pRo+WcRnrTWnX5Tl8xxnZXG7cwHPP4aWXsHix3wM8ZAh3OlTnzihaFE2bclXu2xfDhuXX3Z1V95j81IEeYvR60cLXiXL7W14OkZGKLmN1vycS6ExeJOlNmmT72GOc3t61K7p355wH+OPYe/kyfv4Z9eujYUPOEefhw/g7jDNTCQ/Hb04JA9z3sOjnHiNKEMCXjF7vGncY8eHszGP4cEWXsc5kmv+9BYwi4/w3wC3x03TK6upVLFqEZs24fQ7nzvkNw4cPc75KypTBa69x56q2a8dZp/z+O4aHoV1rTnMWehFyZ9U9RiygwL1m9HrXtpsJVE619vRpTy5jvXnbajICdwYiXHIRTVlFRHB7J5o2xYIFuHrV1gwvWIB33kHJktw69smTeZWKieHWtJs0wXvvYVBr6cVtl/oH8QWj17vGv02+S3/Kz8Szy9j8tNpDZ4GPiMP3P/OflbSy2rePc9/z8cfc3I/dFOlTpzB0KMqXR9Wq3JExt9y0CYBzVDBkCDFH1bjRKl8uQRDyB3p/l510tUUDfQe0A3LyynLkiDqXsbqLfgMYTgb8MXkO3xWsrJYs4aZwv/6aW3SxA8N//omWLVG8OKcPe/TLOXQosCvPoE23tAL7QdvT6/N1XY/tv5uwJPCJodZlrMec5RLkAkuJFt0VuAhlK6vISHz/PTf3M2cOp4X6hOHz5znfXVWr4vHHOYPtRLfNGJIVHT2aDMv9JW+ySE4C9qbX/uiCeJlrAUzJ708aXMbmP6Q9dAL4EBnv4b2inr9vDx7kTDs6dcK2bZYCvGMHNxFQqhT3EbtunQov9gIx/DcDx30MTwJ076AW5BaQQRvT6xfo8p1iAvFW5fxCy83V6DJWd8+6hsjW2FUK10cg5qJnLFeuRIsW3PLp6dOeE3szSvPLP6+9xs0kDxqEy05f1poqeuUK2dicQKxWND0ZNIntSq8fofvfKuQhojz/nd9rNLuMzX9UW+jbUZhZD2kNcLMD4g55ZvLCBc6dQJMmmDULV654Tq+VYeHyz6JF8gemaqql88+ipoeCIbEt6fUvdLkZUrI1d2x+h9HjMjb/aQ0hfsoq4S/cboq0MCQuUwXkkSOcDVP79ti8WVV6NQxLLv9oqAlLql0C9qM3K+/8W+118ekT08hpCWn5ZdDpMjY/A1UhOmUVewqpPZH2Jq59i+hLqphcu5bbGjV4MHeegxo+JdOoWf5RVROWSLsE7Eev9jrY4okTRHl2btnjjj3S7TJWdX2olVUeV1FImYS0+rjZGbFHVQF56RKmTeMU6Z9+4r5OJfmUi9S0/KO6TiyhBgkwejUISylpLtCBHL0tSKTfZawgE4WgyMqKxyxhHW43xu33kLhGLY3HjqF/f85EccMGz4/oW/5RqAW7pVsCjF7donN7cBaxgkrNj/fWZWx+TtIhSSur6GjE/oObXYkWPQ7RqqemNmxA27YYMADHj0sz7M3yj3QFWKx3EmD0eic/4dPniPLsPG6bv+Oty1hh/m5hBSur6Cu4No4D+GZXDmY57VcUf/kyZ7rYpAmnTl9yfjwbsvzjVnYWYYAEbECvlAc2A2rmkyy6EpdUglcb4DJWkJsoSKesRBDSy8Q1nAp9uzES1qkFODqam8QaPJib0JozJ3/3j2HLP6I6KF5euoRDhwQp/hCEWdD3tlZzAFfHRf7dKL8TT7HJLpUwxmWsS5bchXjKKlqaz9ij3CRWWn1uQitataXkggV49VXcdRdq1ODMs3z1i43ltID83zfA9fwrFvLp2Ot367oe+8sVojyvdkmnz2Xstm3cTvTt212yEl5ITlnRUdclcIlbRkp7k1tSij0lDTmfXrT8c+MGVqzgdtvOmcM5qfHJT+hYA5HADJ+UwqYv9R29gYcu38S9yBGBrs2tw2XsqFHcUUajRrlmJLiSm7Jy4VYwICcu58w5bocj4S8JgBWWf5KTuX0OH33EbTa0/sftNBL+vhBeBHvYR/QGKroAlhFfk7EuHUury9j0dHzwAZKSuP10coOe0pSVAFohzHGHOIPKtAZImYZosnFf/fLPiRP49FP9Rssu4tByIaZ3AXBYy/MBndYX9AYwugDiCb1LxL1Gk8vYXbvyjvYeOlR2xPM4ZSXkloZjLnJbGtLexKV2+PRDbbt/cnKwdi23NXfWLNy+La6gSddietOBr0x6lf9lazm9cw125uoQ/EJDQ19//fUzZ5yOanzVHP3JmSaub9fkMnbMGG4/HcA5fB0zxjUjcqVyyopCSwP88k/vylhTBIerIOYvicyVo65d4/Y5tG+PrVuVExpzN2+XrzCzYXluCYRxwRm2nN4Eg+XscORXISEhYcCAAbVq1TL4HVqzW0vmrty2xal0GZuRwXmWo97GmzeXOD1Qw5SVU4sW7f7JigC6ki3+S2UdvivU++xZ9O7NmXZcuKCQyoBbebt8hTmdBAReJoV3gi2c3/X9tOZCev9z/5uamhoSEuLjulwjVMwTl0Kly9h9+7jlVvobOJA7YUD00zRlJbv7Jw0YQ/7QDNfjeyg3l3Og2bYtZ+Bh2CkwonqSQ4wljiA/6JYuKCMCit6MjIyJEyfWqVPH9005BOgiUQo1LmPHj88/oAjgFNTvvxdnpWbKSrT8I+n8jcv3T2Lg+REgOHBE/D756xs3uCXZdu24A4dyA8nwRr7K9rkTCPTSL9+QkJD333//sj5XDsa2yV9kTPtXnKlHl7FZWZwrmSzBfvSMDM6jjTDmv0ODlaesFJZ/xAXiryOcDt/JmabSaRRjIyLQrx/nRf3cOcV07KahEggEegHk5OQsXrz42WefTU52NXQyVFgaMrtFPMX+IvGENy5jIyIixo8f36RJhyJFvtmw4TCdi+ID6pd/JIp1C/iG/MUZJeHwXSK9VNTmzdwgPHWqxMmdUslZnLcSMJlep4ttb4sp/7zwu/eHH35o1KiRfFpr74wC2ktMCOl2GfvLL7OKFy/z5JOfPffcrxUqDCpe/MFevYbx3Bq2+2el0+F7pE5Z3brFbRVu04abLWeKtE4hqn7MTHotWdcV0gugbt26y5cvV119MxPuJEPZcYlX6HAZe/DgweLFH6hbN5LORTdokHjvvc9+/PESL52/ict3hjh8DwfIkpX4rrrrixfx5Zf47DPO/R37mScB0+i1BF3Opa1gxQhAZGTkM888c0t2isY8SbrlnAE0B6a6xYNzRN6nj0S8QtR777WoWvVnii4fqF172z33PG/87h/q8H0cIPD1o1A8yVvbt3NHhE+c6HIQkWRKFqlPAubQaxW6+ups3VPjiafYbPELdbiMfeihCm+8cU5Eb8OGmUWK3J2RkSF+gffXucASokV34xy+6/6lpeHXXzlFevVq7nAT438xxmfpRzmaQC9Dl7b/AaI8H6DX+QE5l7Hx8fGHDx9evXr1tGnTzgkmcCtWrP7qq/tF9L71VvI995TKz9Tw0D+cw3c0BbSbZAnLEhWFr77ijho7cUIYrTZ86xbi42USf0kcesrcDPhoo+ll6Aq7TDYZe8cLo/LC1GVsfHz80KFDhw0bNpT8pk6dunLlyoMHD8bGumx0+PTTvk891UtEb5XKk+u+9oZE7gZGpRB/A2HkTAPvxvjdu9GxI3ckSlKStvKJd/kKn97unx5IhVXwImwovQcMtmH2ol6+f5QfRY9/fDzihYgRg0d872Zyocll7LVr18qUeaRKlclhYbk8w9WrLy1+T4k1HYtH/zEiN0ewQGx41XOB+WTrRU9vDyVJT8e8edyG4WXLtCnSLrt8RRUM4oOODKVXJFabXebk5FSuXHn06NGmlmvdunXCUfTkwpPp9dO5s/Dcflpdxp4/f/6ll14vUeKhh8vUuPfe/3viiScOHvwpM2Xpucm1T33z3O0oqdltt5fqjzhCPM43BwReb/XlFhPD7aDq1g1HBUe3KWcl3mkkTD0BCNav32ChNzc3t127dg6Ho3Dhwps2aXPGI/wW5ckcNmzYdgW3F8K+lUtWfWU22etwGRsVFTUj/O7Tx6YD2+h/ibsHHO1byvRBOBEYQL7kpwGZwkrqCe/fz1mVffut/DetIFcleuMAqW8TwdMBGwwKenNzczt27OhwOL744ouqVauGhISoB/jrr7+W+xZV2yl+IXZXUmdM63MZe7R3yaybqym6fMCiQTgb+JVo0b0Blw9ztcIQpsvMxMKFnCK9cKHYFFSY7L+wEr0A+ktYxYhyCMjLwKf3PyPKihUr/rcsPHTo0Hnz5o0ZM+bRRx8tUKBAvXr1hNNFN83bJvMvGa9kpm11uIyVpJdn2KJBeD+ZjWsJ7DUAirg4zgFQly6Q2EvkzF5il6/zFvfvemCL8DpYwgFIb3x8/JUrV2gDRkVFhYSEFCpUaNOmTe++++5dd91VoEABh8NRtmzZiRMn7tq1y0RuaSG6AEPohUtAh8tYBXqBbRYNwnFAX/JXaaYxazZHjqBrV4wcSU79dJEQdyGxy1eYJheYK7wOlrAX9P6uZ1OosXLdtm3btGnT6LconS7auXOn8EVRUVG8wrxx48YqVao4HI62bdvOnDmzZ8+e1atXDwkJefbZZ9u0aWMizPOI5cM1YaHyw1pdxirTa90gnA38RADuBxjhdCE7m5uLbt0a8+eLHRLs28cZTgt/ERERDRo0KFq0aKlSpTp37pyaKjjDQpguoMN66bVkXZdOF0VFSR+fHhERIVoXlWusxMTEqlWrFixY0OFwvPzyy9WqVUtyLjtmZ2cfPXrUXJgvkV6+Vrp0Wl3GqqHXukF4N9CCKNIG7ZhPTMTYsdzK8J49+eK6fTunbt36ERERNOqll14aO3ZsampqXFxc9+7du3btSm8FT0AVvdnZiIzktm7m2eSZgy5vtyD8FqXTRYbYLV+4cCEkJITfu9+/f38hwML2NgvmT8jkivBNgrAml7Eq6bVuEI4GepGprDlAjqBWXgT/+YezzRoyBFFRyM3Nbdq0qcPhePjhh+nf3CJFitDxNj09vVQpM23OvKiIqY96pvfoUc7WnLcQaN0ae77VY5JBR9Fp06a52y2YWkNh5rTtuXlKeYCFjxgG8xLSv2Us/uLjuZNHVE6caaLXokE4g+zHCFRV+7YAACAASURBVAO+BAzaYZ2djVWr0KZN7v/+18XhcHzwwQdFihShf3MbNWrUrVu3WbNm+d4JobC7WBv2QG9MDOchrVcvblvMgQPo3wGN3uPGYTW/devWeTQAVJOPeWlUAiwsgH6YYwm9y4SZuYTVu4zVSq91g/BWcgR5W0C1GYaLCNwucnJynn++hsPhqFp10IYN2LBhQ5EiRR544IELFy4kJiZ26dKlWrVqBQoUeOaZZw4fDkYvzx7onTsX4eFISSFynYPbc9GqVc6wYQm8GT0/S6TWbsGtbewQoQNgYbG1wdyPaJjC5wVh9S5j9dFr4CD8119/vfDCCyEhIS+88MLmzZsFlQAuAz3IYU4LDFiDXbFiBb86sHFjUtWqSEzMfeeddxwOR4sWLehLk5OTR40aVblyZRoTPAEP9I4Zg+7diTR691tUIGzo88+3axbxcZd4dzN6/xWZlwALK64Mc9riNIQB+YtZwke5sEqXsbrpNWQQPnLkSLly5VavXp2amvrnn3+WKVPmyJEjLjVJByaQWbohgMw0u0t6xYtff/21SJEiDz5Ybdo0brB1OBzdSY8sWbIk/e69fv16kSJFFLMJzJse6F24EI0bkyW4rCzUqHHttbAWDVOnv/gzZ+S2ebM2S3MbC9BAgIW1FMFcrki5LcW2/PDKD3JLUypdxnpJr5eDcMuWLWfMyD8LbNq0aS1bthTWOi+8kViYtQe89o70008bChYsUrr0vQ6HY9CgQXz+Xbp0GTRo0IULF5KTk7/88ssGDRrkvXeCRFkCNcoDvSkp3Ppbx47c7uo/F17v9ua5Zo2zYlbu4zwIVquGe+8NGIxNAljYb7Kzs2M7x57+32mFdWY1LmO9p9ebQbhs2bJCr51Xr14tW7assJr54QtOh+/L9GvR2dn45BN88cUMh8Px1ltv0cxTU1M7depUqlSpkJCQsLCw6OjovFvzgGM0VYAHPNAL4Px5zms+P+fcrf3t04+/gy1bcPYs99/WrYGEsQUAYyNRKYnbVNHIzBuNvPfeF7Vq/bNjx24FCzCj6NU3CBcuXDhdcDJaenp64cKFZSm57XT4PgLQZU/xn1MO3jf9ihV//abmCIX/XPmIjh2ULZzf3/BML1/FGzecc1cTJqByZRw/ngdwYGFsOsCpxPX5LIl+Q2F+8cUNTz/dVcECzEB6dQzCZcuWvXTpEq1AREREmTJl6KV0YC2pdUfAzcG1dHpn7LVrnFcdavaqtMvX+Qj371Cv3HEJc7J5WC29LtVo3hzNm7vQyzMcEKOx6QCPBDooaZK8y9isLFkLsNkt7rkWt5gHz6j/q7eObtGixQ8//ABg5MiRI0aMmDhxYrNmzVy6h+TFOaAT0BhwPZpcMi2NnDSJc4tFfx52GtF0xwC3Y2jozUAK6KI3NRXPPMNtDKHQugf8Wak2F+AdRHlW9PDk7jKWjsw9e/asVKZQSMidzz77f23avDlxYs9du6bevLneEIzVbFE6evRomTJlVq1adeDAgRo1apQrV07tWutN4GtS9+9UOXw/c4YzE0oTOLVUSy+A4DikWxe9AM6c4aasli9XAtiflWoTAU4jJg3TlMYAZZexR3uXTL++kphmf9GzZ+Pq1Z8OCbnLKJjVDMKbNm2qVq1aSEhI9+7d9+7d+/bbbytVRnRvBdmw0QVQtPnJzeVmW7Ztc3lYA72/aNbSXd7kJxee6RV5QgsLc9Zs6VI88ghngeU+8ErG+NtobCLAY4mXGXkPqcouY92/e7OztxgLs5pB2NkPoHbspQ+cJt8O4WRfLo10Daxbxx0vKvp52OUrTH0DGCm8DsywKnplq963L+rU4RzmS+IqF+k/GJsF8N9EgTwkK1f+6MCBA6UTuNMrUpsNgVnNICxdPjWx18ncUhhxaiPQjflHb9zgDha96OZH2sMuX9F7b4quA/DSO3qzsvDqq9x6nByoyvH+gLEpAGcBHxCDJPkeRV3GuifxSK+BMGsahN2LqhSTCywiNpXdgfw5bO6JH37gDkNy/7nv8nVPE1Qx3tELIDYWDzyAX37RCTCPt70xNgXgKWRbrKKHZDmXsVrp9RJm90F4xYoVJUqUOHnSaysqAMeBdmQiwGkuHRHBHUQoeZRNUhKCcjOC7F8kVfSKPn3Fme3ahfvuyzfhUB5vle/aFWPjAT5KlOfdYlkKr+VcxnpJrz6Y6SB8/NjREiVK3HHHHRUqVIiLixMWWGc4GRhEpDEZuemc+c9fMj7AdOYfuI+potdz9SVNOJRBVb5rP4wNBjiHjDnfeRCtpMtYY+lVD/O29V8v/7xKqdBCD5S9f/78+aGhoZUqVTIG4ByyQvseLjfGyG7s6FAPvYLeNohegLPfkDPhUAZV+a6dMDYY4J+IHf9t2hYSAUmXsabSqwDzE0886HA4ChUq8L/yhbuFv7x1y+aQkJDQ0FBjVGggbTd2P47UhoCLVzIJsbAoXgLG0avGhEMZVOW79sDYSIDPEHXR+b0n1yPdXcZaSa8Q5smTPy1Q4I5HHinTt9f79xe/c9WnTxcvdk+hQoW2bDHGHetPP2HWGGJoEQZMB8w83UVO2v4Vr4peD9+9tMbqTTiUQVW+62uMjQS4EzCMik864O4y1lf0Atu2bJkQGlrkwQfvrV+/eukSRe+/u8CuGb0MOUXpwgVulejGDeJfljp8N+KzGtulBRsAsZ7p1VZJrSYcyqAq3/UdxoYB/BsxPPpv8VPxJ3IZ60N6gW3btk0qVKhAgQJ3lCtX+vShqUadojRgANatE0jhb7Ko1hL4WxCpLzgeMOSvgL63m/mU0fQC0GfCoQyq8l1fYGwMwBeJ8uzqqdi9uUUuY31LL7DtscfKFi5ccPPmCbxeTaejdQ/C27ZxdpG5ua5VjwP6EGdgXjp8j/GwtO76Vn+6MoFeL004lEFVvmstxsYA3IMc7eWpzwhdxvqW3qyszaGhRZKS1gg/id3XhD1VKP/+7dto354znJf4ZZEP4DDA6fA9Pd3Fz7PEI5JRAXpKqAn0GmXCoQyq8l2rMDYA4EVkePF0FkG8wGWsb+k9dmxmxYqPCdGlYX2D8KxZmDRJkjln5C5i2dIaILalanf5Op/m/l2LgPz6NYdeAAaacCiDqnzXfIy9BTiG0LtC2Nekw9RlrG/pnTWrf9u29SmxooDWQfjKFW7//TWPzuuuAp8SQc3FMJkToaSlxsdmE0fTSin88p5p9AIw3IRDGVTlu2Zi7C3AfYHennsPdRnrW3p79Gg8cWJPEbSiS/WD8ODBWLPGc925FE6H7zte1eXw/VuAd2ys7m1+kcpMes0z4VAGVfmuORh7BfAqMnd11XOH4V3G+pbemjUr7tw5RYSr+6WaQXjXLm6HS46mw1O24ERFYqZ23LO4XFJcABT3VLsk9pMLk+k124RDGVTlu0ZjrB/gJKf7ck+dhncZe7DX/e6nb7vzY0YMP2WVmrpOZeYKg3B6Ouer9ISijxFJeUz7ElldiMQWKjkYknh2h0ScX0eZTK8mLxzKsJl31ziM9QM8EOC93nvqTcOHY1qTcF/RqzBlJcez3CA8dy7Gj/dUW6n7ixbh1GHge6KwDAU8rZZL5REgcebTC8BKEw5vIDcCY50Aryd9UdFZDN/jTp9Gk8q/pV93WbCRI8fweOUpK4XXiQbh6GjOT3iyrvPK8nf5rieG4h2AUwFCo9ZqWEKvT0w4fIexHoBvEH+Ls1U1X6ca4/9at1sBFfNuqZmyknu7cBAePpzziabvFxuLedRl5HngY2Kvpjc3fWWwyVNW0etDEw5fYKwH4BFAR1UfcovavNaty4Xc3G1ynJgXr3LKSqEAibsHzGtdr33DA1mZBu1CuAV8RzSXkYDX3nDefvvtP/74g8L5xx9/vPPOO/TSbgGr6LWDCYe1GGsGeCvpgiqUwKO9S372SeTevYcVIDHjltYpK8kyZGRs7/jh+TX925365rnbUVonjuXxWUuUl44AOadCPp2HO2fOnKlUqVIGOWY+IyOjUqVKdj4f2EJ67WPCYRXG2gBOA5oSw0APHQxHe5fctWVnnz5XJPEwL1LHlJV7YRYsOPXdd5HANtGXsKdKq7j/L1FeGhPLKhXJ5ZL07t17zJgxAMaOHdunTx+5ZHaIt5Zeu5lwmI+xNoBHA20BT+ufR3uXzExd3aPH1SNHDrrjYV6M7ikrWqS4uN2tW8fFx+d9tAu/hI2BIZU4gg0jurSC2wPFE5WuXbtWvnz548ePP/HEE9c8W4EZU3B9uVhOrz1NOMzEWAPAe4ny7Hoarnu78tYaW7ceHTjwEgXDgoA3U1Z88UaNOr948UlRUY0fhJeReayPgfPuwiMxXwHpMrdI9IwZM4oVK/aTpGNLpeesvucLeu1swmEOxmoBzgRaAsom++A056ybq7Ozt3fuHH369H4RDOZdejlldejQwS5dojMzt7uX0PhB+JTT4fsGKaIOAwuk4p1xOTk5DocjR5sVmPNhC//1Bb1+YcJhNMZqAZ5EAM5U6gLUUnL9+uPDh19wh8GMGC+nrLKytnftevXAgUMKZTN4EP5v58NQost8L3WkoKeDjhwOH6Gh1PLie74ror+YcBiHcf+WLas991xSUpK4EYTXR0iH2yuMEocpvZmZ2zt0iImM3KeAhFG3vJyyWrr05MiRnv/QqByEc3NVbEsCWX5bSGwqewCXXcU4w8NBSoxeV3m5X1nvhcMbFL151mnF1T8kpFrp0kkrVyJb5hSjHDJxNdpdWPkxlF5g28qVJ0aP5qZwzf7PmymrhARusio2do/KQqoZhDXs8j3mdPi+NV+GnH3lN4JLtyCj100kogg/NeHwDuP+L71ULSQkqXRpdO6MzZslMJ5Olo7cTvehwhPSm5a2o02b2KiovSrB0J3MmymrMWMi588/penVHgdhDecJguwoHEiUmqlkpyEvyoF+77bSd5ozL0FDDlLxBidfPNu/c+dqFSokffIJqlXjDlIVYXyK9DPhQEHBJQEhvcC2hQtPTpp0ThMbOhLrnrI6fvxAp07RGRkSk1Uei6EwCGujF2Qdbi7Z398LiCZy3AWscpWsv135mt7AMOHQ/ieAA7hixaT9++FUqvMxzsrmTCZHSHelzMzMFR8Wux6/hHb9mzd3tmqVv4hK4w0M6J6yys7e3qPHVW/MwuQG4QEDrp0+fVpaRgqxh4DWxM/OLpJoIl555ZWhmv8SKLzA0ls2oDeQTDi0YJwPMP+UEOPXZ+GVeKS4fBsnJyc3b962SJG7Sxd78K67ir7xxssXLy7iEZ09+/T06WcNxFWUle4pq5UrTwwdelGUm45L4SB86NChZ5+tfuedJe677+kiRe7u06c/b9iolpsE4uMuDJiBz/t+7nA4ChYsuHbtWrWP2ymdPegNPBMOdRiLAaYYd/4WxbejWDOqVKelpT3++DNPP92vYcP0sDC8+25O5crfly59f0zMcmBbSsquVq3iUlJ26QBDzSP6pqxSUnYZ+E3OD8KLuz9ZrNh91asv5U8IeOutpP/7v2b16r2rjalsYCYGPDHA4XB81Oqj6tWr33nnnf4IsG3oDVQTDk8YSwN89ixapaD1Re5EPfJtPPj5GuX/r7XoUItKlYaHhzfg8Zs+/ezs2afVoKgjjb4pqwkTIn77zeAiVXj04eov5qHLS+Pdd7PLlauxZMkSTQDXrl3b4XB0e6Jb7hu5KUtSqlevXrBgQb9ToW1Db8CbcMhjLA3w99Gom4r9EdzByFu3PlfuiZdf3iWit379uOLFStw4O/HG2Ynn985oFnYm9ugP/KWx/6/+3GMbfv9UU54H/pzTJvxk/PEpmp5STnx+79f33F1KJISwMFSt+tOHH3ZRT29SUlJoaGiBAgXWfLUGFYCv8Nlnnzkcjueee059JnZIaSd6/cgLhzyK+k4hlwB4ZyTeuIkfr/IZlrv/0bp1z4s67rvvZt9Z6M4To18+O+6Vs+NeGdRo4oQ2Q/mwgf8/NeblkDsLHvmmlvo8T499rd2ri+f36KH+ETUpV/etdn/J8iIhhIWhRo01b7wRpgmnq1evVn+u+p0F7lwbvnZAf06F7tSpk/1NI0V1tBm9fueFwziMJQBun4yPknl6G7za4PnnF4g67muvHXz88Wdpi1KXsTTGkMCxY8cqVqyoKas//sCgQZqeUJU4IyMjJOSet9++LpLDU08N/vLLwaqyoIkykNI1pXppTmHmVOhu3XLFB7HQpPYN2I/eIDThcP4JEAP8w1W8kYrdkTh7dtOvv5Yq8dhbbyXRjtuwYfoDD7z8ww8/CjsX7zJWGON9eNasWW3btlWfz/XrnIP1S5fUP6Eh5ccff1K+fPuwsFwqhzp1ThcvXiYiIkJDLgCmcmu/MetjQkNDq1Sp4o/oArAfvf7uhcOJogEq9L4Ijt6J0XxWQ3v2LlHswUqVvq9Va3OVKj/ee+8zrVt/JOp2vMvYTMVNDtp6OdCjR4+JEyeqf2rKFPzyi/rkGlJu2rTp1q1btWrVefDB16tVm1Oz5vqnnx5aOPSeH2fP0JALAN6NyRzuobi4OE5h/llbBjZJbUt6g9WEg6fUZQTukoTWKfQPwZ5PPun+f0/WrFm3Q4euciscw4dj/Xoje1fNmjV37lR7mv2//+LDD3HrlpEFAJCUlNSrV69Dh7iDjHJzc2fPnl3n3bdLVHqwVdd24fPDwzeGa3jfZaAZMNDVC8IqgLff0JCR75Pald5gNeEQA/xzFDd3tfV8HsBvvom5c5V7zenT3CKx3CYI5Wfd72ZlZYWGhqamKnqjcD6Wm4s+fbBli/PaoH9jY2NHjhx5/bqL4+bt0durL69+MOHgnrg9Tyx8YnHkYlVvSwN6kE0LIme0WYRnVVnYKJGN6Q1WEw4hwMlbD6FeKkbHcJGHDqFYMbh2Yvr517gxRw7/9TdwIGd/achP05TVhg3o39/tGF695Th3DoMHo1mz3ClTcuPcjs+m9B5MOPjb2d/un3N/fFq851dNIBsGj0kl/Mb/HLvbm95gNeEQAny7cxSaXeNixo3Du2KjojDnQkl6OpYsQXdyIMORI+jRwxiK1E9ZpaaiXTtEqnAoL4WOOO7SJS63Xbtybt/OvXoVAwdi40aXNEJ6DyYc7LCtg2f9eQPZ/rHQJZ/8i0jOdtK/fvamN4hNOCjAXR7tkPlqCtZfgJTaTOn9b60tNRUtWuR1vz59sFdxi7/Kbqp+yurHHzF9uspcPScbPRrr1uVQA+arVzF5sstTIno9688XyMELQxQ9ZntyuOFSAhtc2J7eIDbh4AEe3KH7X8U23ux7xl1tBkDpzczEsmXcf/xv715Okfb+p3LKKjKSGyrVfR2rKlTbtoiJUUopoteD/nwL6Eo8XSkfFLwAOKz0Urvd8wd6g9iEgwf4zxrL1hRdklT/LffeQ797+cAq54bV3FxOeT7iyT2le4bCGJVTVrm53OfuBkn/b8LstIQbNUKW4lkL7vQq6c+jiZdJj57u0zmrST/6+Qm9QWzCwQG88PKpon+1KPeWu08sOvZmZeHAAW61hv62buU+F735qZyy2rwZffsa85lNS/vhhxD6//pvNvvGDXqTC0jSK60/ryWfu06txCUX9wvFAd89uW9j/ITe4DbhwL7DKLxsVZ1l1apVEwFM6QWQno7mzfO7U3Y2t3SkYwc7zULNlNWtW9yfjH//pQ8ZExg71mUw/+efvAk5mrskvRL68zmgCXHRnksfDZyA/9AbzCYc48ah0s9ohS/7fSkCmNLLf/cOH+7SNdevhyjG5banCzVTVr/8gilTPGWkeD8pKWndunWiJJGRaNsW+/cjIwPnzqFrV2za5JJEjl4X/TkV6ESOR1G1XO2Sv19c+BW9QWvC8eabGPkHwoC/IfILTb97/5ttHjoUonXRzEx06KB/FcfjlNWlSxxjrivQ2rr9nj17+vTpI7LE4LM4dAi9eyM8HJ06wd31hQK9efpzxGJ8TY4mM1ov0FZDM1P7G71BaMLBG2kkX0cbYCzXF0QAK3ePlSsxWtG/rNzjaqasBg6E4LhMuZxk4ydPnjxjhs41VgV6ef25fa/2GQ0zsEb27QFwww/pDTYTDmqkMY0Y6BJPseoBTkvjdvxERWnuqx6nrHbsQK9e0HdaiNBuWXPJyAPK9J7Yc+LQK4fmdvRgVarv1fZ5yg/pDTYTDmqkcYLMne7I6zzqAV64EJM8nY3k3iOVp6zS0jid/JTHNRj3fAEFbVkquXScAr1Hzh9J/CAxtl1s5d8qq7V/ln6J3WP9k97gMeEQ2jbnEnuDkfldSiXAN2+iVSvEq7ACzs/a08bA2bMxYYIwudrwqVOndGvLwnfI0ht/MLpfdPK7yf8c/EeD/bMwaz58wD3KdjF+S2+QmHBQtZnvObPI+odgBlUlwLNnazZjVJiy4p14pKT4sjfL0Rv5c+S1Btf+XfzvwYSDLvPPWgs7Dbig9Rmr0/szvcFgwkHVZr5jnCPKs6u9vhqAU1K44Vc9b8pTVkOHYuVKq3uq6H2S9J7ccTLl7ZQrI67w6GrePyh8RwowSnhtx7A/0xvwJhxCtZl2nq6AmwsnNQBPn47Zs2kuHgIKU1Z79qBnT8P2D3soh/xtd3qPnDuS2CIx/qP4w1GHKb0S9hvyeYrvfAm4+MMX3/f5tZ/TG9gmHCK1me8sv5MdqqLN5SqWkeLjueH35k1VXU5uyiojAx074vhxVZmYmkhMb9zBmM9ikt9LPn70uBBdr/Tn7YC9j1jwf3oD2IRDpDbzNFwhyvNqCTQ8jsCTJmGh3O5W1/zkrKzmz8eYMa5J5a/27Nmzb98++fte3RHRe/7H89caXDu74qw7ul7pz/29KqTZDwcEvQFpwiGpNvPdoRc5iUeqaygDrN5lrOSUVUwMWrdGYqLUi93ivLHEcMtMIkJI76nNp1LeSrn87WVJdPlInfPPEwAb71sIFHoDz4RDUm3mu/EycpJlrESf9miJpcZlrNyU1ciRWLpU+qXCWO8tMYS5yYUpvUfPHk1qmhTXOe7Q1UMK9Oqcf44DxssVwffxgUJv4JlwSKrNfIeJJ/TKH9yjMAKrcRkrOWV14AC3VUB5zy0MssRQgwVP76HYQzGfxCQ3Sj72zzFldPXrz3+oKY5v0gQQvYFkwqGgNvP9pD/wiVKPUQDYo8tY9ymrzEx06YLDnvxOmK0tCyvM03th8oVrDa6d+eOMR3S90p+FL7ZTOLDoDRgTDgW1me89/I7zy0pdSQ5gjy5j3aesFi3CKE+Ln+vWreP9LSuVybh726O3tx/dPuWtlEvjLqlEl0+myn+dceU0NaeAozcwTDgU1Ga+O1wjrl7meegbcgAru4wVTVnFx3OTVaK9hx5ebP7tPcf3rH91fWy32EMxHj53RWxL+98wv8BmvCHg6A0AEw6PajPfEYYAKk69lARYwWWs+5TVd9+pXWcyo4NK55mFKx9fWf/q+qOnj4rgVHOpc/5Zuii+jA1Eev3dhMOj2sx3mL/Iwq+KreeSAMu5jBVNWR09yrnXycjwZR+VePd0JNZPbD+6vRpWJdMEhv4coPT6tQmHR7WZ7863iINided9uQMs5zJWOGWVnc15k/r7bwl8fBm1i/uzdXbCWf4kFEk4PUYGhv4cuPT6qQmHSrWZp2cU0F7RvbgAMhHAci5jhVNWy5dLu8WaPHlybKzMcrPgjaYErwItgC+w48oOb+jVY/+s6KHWlMp6yjSg6fVHEw6VajPfrjuJ8qza6lgEsKTLWDpllZTETVaJXKJbY4kh22kzgE/BeQhKkPYI63HIFSXQpj9/Dbh6pZUtp1U3AppefzThUKk28/0jA2hODpJW3V2EALu7jBVOWY0bJz6u0BCfGKpLKpVwCjFT4Y4BNYZebfrzv4C67xSpopsSF+j0+pcJhya1me8P44FW2jayCQEWuYylU1YnTnB7idLT8/uclZYY+W8VhrYQRcO5SEYtJUXDqdZLbfPPNjvoKAjo9SMTDk1qM9+zD5A+rdGNCwVY5DKWn7LKzsYnn2D37jx0fKwt86VwOzLbKHq12T/PAyRPDxX+lbEwHBz0+osJhya1me8l2WTs1W5JTwEWuozlp6xWr+YOzqW/RYsWSfpbpglMD6QB3cVHZhtIrwb9+T+HnkNNr676FwQHvX5hwqFDbebbeSr5+tW+JMsDHB2dTF3G1qxZc/36vW3a4MoV9V3I/JTjiUMC18k5A+nVNv88FCBOec2vtuc3BA299jfh0KE28+17nCjPuzw3tnsKHuBffkmdMCGrYsWKd95555gx6b/+6p7QdzHrSe0WiQtgLL0a9OdjgPPbW1wmy6+DiV6bm3DoUJv57pJLVn097SKQ61r9+/evWrX2I4984HA47rjjjgYNNqXZZmxBJLFIGSqxpm04vRr056/lZGl1fJDRa1sTDt1qM99hfiG9/Jae3pOTk1O5cmWHw/HMM62KFHn8rrtCNokO/NKTqxHP3AI+Ji6sr0vkZji92vRniRL5ICr46LWnCYdutZnvM/8S9fIvzR0oKyvr6aefdjgctWrVKVx454MPzqpSpUqhQoVG6zv7SPP7FR/4juyjOi2dxgx6NejP0oWyOjb46LWnCYdutZl2mC7AEHqhNnD58uWQkJDChQtPmjTp/vvH/fjjrlatWjkcjvr166vNwqR0a8jfoxWyuZtErwb9WbZo1t0ISnrtZsLhpdrM95Z5ZKS6prnrREVFPfjgg4ULF964cWOHDh0cDsdXX32lORdjHzhLTu78WuJzl77HJHr9S38OVnptZcLhpdrM9+hLZLDS6H+Yt8TYsmVL1apVCxYs6HA4RowYQQnxTSCVnJfdCVB0PW0evX6kPwcxvfYx4fBebeY5+wTQ4n9YaLd8/vz5kJCQevXq+YZY+tZcYCQ5q+kcjZIOmEqvv+jPQUyvTUw4DFGb+R6+hBjxqz4rcKXrYURJSUnSoFgZu0ytBmEqvf6iPwc3vXYw4TBEbeYBiyX0LjOXcfY7RAAAEBVJREFUNofz99+ncu3atU+cOGHY+06ST/fRqvIzm15V+vPvQI6q0pqUKOjp9bkJh1FqM99B+gG9TOoqedk6HHl9JjMz88cff3z55ZeNed81YnPSFbitKj8L6PWsP28B1qsqrUmJGL1EsM2bo3lznD1r9X8Gqs18B1lNNE8zrZQpvQBu3bp19913G9A1c8lyV7iGI3MtoNez/pyrbaLBAEG5ZsHoJfLwlQmHgWoz367JxKD/d9dGNvSK0nvz5s2xY8e++uqrBmS/kPzRcT2XWDlba+j1rD+PB+KUS2riXUavU7hnzuDee7F8uaXDr7FqM1+VwUBXZ6XIv3v27DHQdsr52eu46667atWqZcB37zHyF2eCS5k9XlhGrwf9OQbQWHKPVVOfgNErkNXSpXjkERw4YBHAhqvNfFU2knHMueJiuE8MOvYKBOdFMBloC/QABH481GRnGb2e9Wctq3RqqqY+DaPXVVZ9+6JOHZw+bQXAhqvNfFVSyXrpLJjkE8NIenOAL4FmgOKRLq4tlHdlJb0e9Oe1wHbJMpoeyeh1FbGVJhxmqM18bUYirmFc3z59zfCJYSS9c4iasNW1CdRdWUyvkv6cTf4GqSu2sakYvW7yjI3FAw/gl1/MHX5NUptJbZb2WnqxykUYtxArlJFh9B4kq9NThXlrCFtMrwf9OUJDyQ1MyuiVEuauXbjvPmzZYiLAJqnNwM2bN4/9fYxTR6dJVc0mcQnEHVcvQLtDH74G1tPrQX/2hWAZvTJSnzABlSvj+HGzADZPbeYrNJZ4Lc+WqZ1vo7OBfuRIhGj95fAJvUr6s/6q6H+S0SsvO/NMOMxUm/Pq8zf5pCSOy+Vr6KM7M0nZdDnioiX2Cb0e9GdaOKsCjF55SZtnwmGa2pxfmSzgA18uReaXRBTaSz53fxLFar70Fb220p8ZvYr9xiQTDuPU5qws+bOxphDtVO+HpaJc9N6MBVoCfQH5UqvM2of02kd/ZvR66i2Gm3AYpzZPnjx52TL5LUVHiYLqPBLBUz3Nv58J9CaTVUaYFvqQXvvoz4xeFb3WWBMOI9RmVZYYOeT8ge9UVNCaJD8Sndmg04B9S6+s/nzKGlHmvYXRq0LcxppweK02C31ieCj9T8RTrLo9dx6y8vL2DqIIGOfn3ef0SuvPv8GkZXZJ8TN6JcXiFmmUCYfXarM2u+UzhJnNbtWxOCKKnNXSX9tZh8pl9Dm90vrzbWCYcsGNvMvoVS1NQ0w4vFCbVWnL7rXpZGl/cn8/Z4/Rkyw+J0rc1B1lB3ql9eevNO+40C0ERq8W0XlvwuGF2hwbG6vHbvk34m5G6jgCLTX3Iu0k8rl72IscpB61Cb0S+vNhYIFUiU2IY/RqFKo3Jhxeq80ay0qSXyTK8596HjXgmc3k7fMNyEmUhU3oldafrTqkm9Er6hWeLr0x4fBCbfZULMX7/+2eHaCYwKSbl4CmwGAlp+q632wfeiX05xngzk8z/8fo1S5j3SYcXqjN2kspeGIR0V0TBDEWBNOAbmTJKsWUl9mKXrH+fB34xpRaizJl9IoEou5ShwmHRrU5NTVVXVFUpIoh9MqfCaQiC+1JxhF/N/9of1DdE7aiV0J/XqquGt6lYvTqlZ9WEw7VajM/t3zy5Em9JZN6ri+xc5K6Y0rcOvK5u8SUvPlM7UavhP5sYu3zsmb06pWxVhMOdWqzBksMTQVfRXC6qukZvYn5I7OHm/K5S8tkQ3rF+jMtq2kBRq8XolVvwqFObdZmiaGp4ElEj7VgJeMW0JkcmX1DU/k0J7YhvRL6s+ZqaXuA0atNXuLUKk04PKnNOi0xxKVRvB4IdFdMYMjNb5WOzDbkDXwm9qTXYv2Z0et1j1JjwqGoNu/fv79Pnz56LDE0lX09UZ5NXcngT3JYqalYOhPbll4r9WdGr87e4/KYsgmHJ7U5IcGSxZwb5Ejr2S4FN/KCPzJ7lJFZKuRlW3qt1J8ZvQo9RPUtZRMOT2qz6td4nXAEOdg61+t83DO4QXLu7OHIbPfndMfYmV7L9GdGr+7+4/qgggmHotrsmovJV1uJ8mz4HtRcYISqI7MNrJ7N6c3Xn6cApqlWjF7jepSkCYcntdm416vIKY2YLk5XkVJTkqXkj4K1ptQ2p5fqz4mRiZikSZoaEjN6NQjLc1J3Ew5XtTkpKen2bZ9ulh9Nzg0y8MzoE2SSeYxn2Ribwv705uvPph10xOg1tFM5TTgub9v2+/jx3/btu+a5527PnMm/g7fEuHHD5JVQ5QrtJePkEeVEqu9qPDJbdb6eE/oFvbz+vPWHrX+O+3P06NFz5sw5f/6857qpTsHoVS0qlQljYycWL1m8aOkK5Vs+9eSXj5aq+dCD5fft22eiJYbKgvHJMolXR0N0uVzgK+J556KmEhiT2C/oPZhwcOSqkXeVLf7w/a8/9VT/ChXaFStW5uuvvzVGBACj1yhJ5uWzYsWKe0tWqFfvYlgY+P9q1FhTtGjJTZs2Gfwm3dlNIgBn6n7e+eDvZBj3UbX8gt7t57eXvv/B51+YTzvDm29Glynz/KxZxjj4YvQ6+6JB/z7yyFMvv7ybthYfeOqpfn37mvb1o7XkRwh1e7U+5pr+KDG9nOgaaeGVX9DbY9Anj5fvKOoM//vfiVKlygpFtWcPGjXi/tY3aYLDWpyQMHqFYvQ2nJKSEhpaKiwsV9RgtWtvrV79f97mbtTzOWTiarQX2SWRHHpa58DJvax+QW/NOnWrV18h6gxhYShV6tGLF/O+N/bsQdOm2LOHq+KOHWjeHP+o3lbJ6HXvGPpjrl+/XrRoCXd6a9X6q2bNuvrzNfzJ6WTpKE1XvjnEU0cz4Iquxw16yC/ofbnemy++uMyd3pIlH75yJU98jRphr0AP2rEDCg72RcJj9IoE4u1l+fLP1qq1RdRgTz7xaf/agzAE2GHuvjm1pT9FlGddx17jN/Ksj06LpxX0C3o/GfLpI//XStQZXnvt8H33PUQrEhZGg5oDjF7NIlN+YN26daVLl69T5zRtsxde+P2++x5KTk5GJvAnMAgQ/K1Vzs2su7nEsHGE9uwPEDcdNjgZ2P70LopYVHFexaL3lapadQbtDHXrnr/vvkoLFiykohfSS5PRu8oBRq+yfPTcnTXr1xIlyjz++HtPPdXjoYdqPflklWPHjunJyNRnZpNNC5rWnuPJKUSfgfsz5Oufnen9O+7vHrt6lJ5deuaZmWfOnKlSpUa5ci889VSP8uUbFS9eZvLkqULhCenl491jhOmFYUavUBqGhZOSklatWjV16tSdO3dmZtqgs7vXLJIowOvdb8jEZAOfk0MJY2QSWBttW3oXRSx6dsmz9f+of+Vm3pdtdnb23r17p06dumLFirg48RFsou9efv5ZpSwZvSoFZX6ybOI81cpv4+7AQNX1+pnozGRqVPUzJia0Ib3CIVd9zfk5Z37iau/e/PlnNTkwetVIycI09NvYAowXkDXbJBW120PQ/VlFSquS2I1e9yFXvSToem+jRnlLRyqfZfSqFJTlyYQY61va8Vjkq0R5XuUpXQyxzfrcyDPEPL3S83370KtvyPVcQxUpGL0qhOTbJKZ+NfcmJ9krVDAT+IxMVsUrJPLBLZvQ682Q673UGL3ey9AlBzrpHxbGmb8JF+Jd0tnkYgVRiRUmoqaRBAdsUtz8YvicXh8OuVQKjF4qCmMCwul+4YSEMbkLczkGA8w/Egici4T5CsLbiWr9myDGNkHf0uvbIZc2AqOXisKYgJBegJuEaNTImJwlchF+G+u24hoA9JDIG/yR2QMAA7fyS71HX5yv6LXDkEslxuilojAmIKIX4PaOmP4TYvy3xrf9SQZY0R5demS2mhlpjS80JLlP6LXJkEsFyOilojAm4M6qe4wxb5LMJRPQ6nTuOnFtI1KPJ5LFpKOS77BFpMX02mrIpQ3A6KWiMCbgzqp7jDFvMjCXYUAnQXabyGj8uyDGfkEr6bXbkEtbg9FLRWFMQMSqud+9moq8QH6HEznh/pve35w9exYXTTwyW1N5lRNbQ689h1wqGUYvFYUxASG9Wg3fjCmBXC7Cb2PRFNdtzKk+x+FwlCxZMqF9Aj4ErsnlYpd4C+i17ZBL24DRS0VhTEC03sv7TDAma6NyccN4+fLlhQsWrlSiUkjhkMrFKifsNM19uFFVAEyl1+ZDLpUio5eKIvgCBOMhXYYULly4duXaN168sbnq5qJ3FX3sscc4FdreP/Potf+QS1uG0UtFEYyB8+fP33HHHUWLFr1w9gIqcPbMw4cNdzgcTz75pM3FYQa9/jLk0qZh9FJRBGlgypQpISEhlStXTjiWsHzx8sKFC1euXDn6SrRdnPjINIvh9PrRkEtFwuilogjewObNm4sWLfroo49yKnTt2txpD9lOJz4WbFTUJXgD6fW7IZcKjNFLRRHUgZUrV95xxx1lypQRH9TiNsVlEzEZRa8/Drm0CRi9VBTBHvj555+jo6NlpcBjPNgWTq1gxJyz/w65tI0YvVQULOBPEvBy7PXrIZe2E6OXioIFvJDATav9VOumNwCGXNpOjF4qChbwQgKniJ9qC6e49NEbGEMubSdGLxVFkAaaNWu2fn2+Y9gtW7Y0bNhQpywsnOLSSm8gDbm0dRi9VBRBGoiPj3/11Vep0+k6der8+++/3sqCYjzP25zkntdEb4ANuVQmjF4qiuANLF68eMyYMQBmzpzZr18/vxCESnoDcsilDcTopaII6sAHH3zQvXv3cuXKidd77SoVNfQG6pBL24TRS0UR1IETJ044HI6BA9WfreCduGZ661JPmd7AHnKp6Bm9VBRBHejevftXX3316KOPWjf20m9jXTPVCvQG/JBLeyqjl4oieAOLFy+ePXs2gEWLFvngu1eIscg5nnybSNIbJEMulQqjl4oiSAPx8fH16tXLycnz+/rKK68YMOesT5aZwE21T7rTGzxDLpURo5eKIkgDTZs23bBhA628V+u9NBeTAwcOoN/w+Pof7/vux5idF44G25BLpcvopaJgAbtK4D8zTMG38YIFnIvsNh3SGnQ82rhJTvPWaVVn1xWel2vXahhfLkav8TJlORovAee3cVR/vP8epkzBtqgdLy57scvKkW83vt518Hnj3+gPOTJ6/aGVWBmdElj/BzfwJvfH2V5nK4yvUP+P+uOmpLZp47wdZP8yeoOswf28un/9xdEbF4fYa7Fj/ubsw6ZMwYcfutRK6NZT6KDXJVFAXDB6A6IZg6YScXEID8c33yCNnEh+4gR3OXmyS/0Dm1hhVRm9QmmwsB9IYN067ljG5s3RsSM3Dnfvjhs3XIrN6HURB7tgErCVBCIiMHMmJk7E2rXIyBAXjdErlgi7ZhLwFwkIv3v9pcz6ysk0Z31yY0/ZVwJs7LVv27CSMQkoS4DRqywfdpdJwL4SYPTat21YyZgElCXA6FWWD7vLJMAk4HsJsFkr37cBKwGTgD4JMHr1yY09xSTgewkwen3fBqwETAL6JPD/C5jj2StCLD0AAAAASUVORK5CYII=[/img][br][br][/left][/*][*][b][i][i][b]ABCΔ[i][b]∼ [/b][/i][/b][/i]PQRΔ[/i][/b][i][b][br][/b][/i]Mivel [i]ABCΔ∼DBEΔ,[/i] az a [i]B[/i] középpontú β szögű és AB[i]/BC[/i] arányú forgatva nyújtás, amely a C pontot A-ba, így E-t D-be viszi át, az AEDC négyszög EC átlóját a DA átlóba viszi, így az (EC)([i]DA)∢=β [/i]és[i] AD/CE=BA/AC [/i]. Másrészt az ADC[i]Δ [/i]és[i] ECAΔ[/i] középvonalai P[i]Q[/i] ill[i], QR, [/i]így teljesül, hogy PQ[i]/QR=BA/AC , [/i]tehát[i] [/i][i][i]ABCΔ[i]∼ [/i][/i]PQRΔ.[/i][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAT8AAAFkCAIAAADZjavIAAAgAElEQVR4Ae2dCXwURdr/R0yAIWLCmXAICoQjHFnEYIAXWQRZFCJgXiIrl1weoCJEiStxQWFFYNUQAZdXRbwVuVnJhiignAuRSwXyJ2RXDDdBOQRCIPV3bFKp9PTM9FHVVdX9zCcfrO6prqr+PfW1nnn6qRkPghcoAArIqYBHzmHDqEEBUAABvTAJQAFZFQB6ZbWcxXEfOnToqacmdurUs3fvBzIz3ygpKbHYIFxuvwJAr/2a8+9xyZKlkZHRrVq91KnTlwkJyxo3vj8u7vbTp0/zHxmMwIgCQK8RtRxR9/Dhw1FR0d267U1KQvivZctnBwwY5Ij7c9FNAL0uMrZyqzNnzmrefDzmVin06VMcEVHzzJkzrpND5hsGemW2nqmxP/DA4Ntv/1BFb1ISatSo29dffx2oyaSkQO/AeW4KAL3cpOfVcWpqWlzcK/701qrVND8/P9CogN5AynA8D/RyFJ9P1+vWratdu8V9910kAb7zzqxbbokNMiCgN4g4vN4Cenkpz7Pfhx4accst9/To8R8F4Dvu+DwyMmbjxo1BxgT0BhGH11tALy/lefZ77dq1V16Z7fXW9nrrV6lSvWrVjtu27Qg+IKA3uD5c3gV6ucguRKfJyWjGjKMHD57v3BktWRJiSEBvCIF4vA308lBdjD5vvRVt2oSOHkX/+Ae6+26NMY0ahS5c8J0vKUHJyRoV4BRfBYBevvpz6/30aXTzzejIER+9P/6IoqPRgQPqwUyahD7/HF28iFavRs88o34XjrkrAPRyNwGfAaxdi7p08aGr/I0fj55+Wj2SggLfyeRk378FBep34Zi7AkAvdxPwGcCMGeixx8rp3bED1arlW2bhJZECQK9ExqI51ORkNH9+Ob1Hj6LevdE779DsAtpirQDQy1phQdvHISvsPH/0EerQQdDRwrA0FQB6NWVx+EkyZIXpLSxEt96Ktm93+L076faAXidZU++9qEJWGOD0dPTww3obgXrcFQB6uZuAwwBUIStM7/ffo6goBNsEOZjEVJdArynZJL/IP2SFAR44EL32muS355rhA72uMTVxo/4hK0zvqlUoNhaVlhK1oSiqAkCvqJZhNi7NkBWm9+hR1LYtyslh1j00TE8BoJeelpK0FChkhQGeNQsNGCDJzbh7mECv6+wfKGSF6T14ENWsiQoLXaeMdDcM9EpnMqsDDhKywgCPHImmTLHaEVzPWgGgl7XCwrUfJGSF6V2/HtWv79sYCC+RFQB6RbYO/bGFDFlhgPVs2ac/PmjRiAJArxG15K8bMmSF6Q20ZV9+DZxzB0Cvc2yp505ChqwwvYG27OvpBerYowDQa4/OovSiJ2SFAdbcsi/KncA4EPwCqMsmgZ6QFaYXtuwLPjtg7RXcQDSHpz9khQGGLfs0DUC7LaCXtqICt6c/ZIXphS37AtsTPGeRjUN7bPpDVphe2LJP2wg024O1l6aagrdlKGSFAYYt+8KaFegV1jT0B2YoZIXphS379C1BqUWgl5KQwjdjImSFAYYt+2KaF+gV0y70R2UiZIXphS379O1Bo0Wgl4aKMrRhImSF6YUt+2JaGOgV0y70R2UuZIUBhi379E1iuUWg17KEkjRgLmSF6YUt+wLaGegV0Cj0h2QlZIUBhi379A1jrUWg15p+klxtJWSF6YUt+6JZG+gVzSJMxmMxZIUBhi37TMxjtlGg16xyUl1nMWSF6YUt+0KZHegVyhysBmMxZIXphS37rCxkql2g15RsUl1EJWSFAYYt++IYH+gVxxasRkIlZIXphS37rOxkvF2g17hmsl1BK2SFAYYt+4JMAaBXEEMwHAatkBWmF7bsM7SWkaaBXiNqyVmXVsgK0wtb9gWZCECvIIZgNQy6ISsMMGzZZ2UwI+0CvUbUkrAu3ZAVphe27IswF4BeEazAcAzUQ1YYYNiyz9Bs+poGevXpJG0t6iErTC9s2ec+KYBe7iZgOwDqIStML2zZZ2s5Ha0DvTpEkrYKo5AVBhi27POdGkAvX/3Z9s4oZIXphS37bO0XqnWgN5RCMr/PLmSFAYYt+xwnCNDLUXzmXbMLWWF6Ycs+cysG7gDoDayN/O8wDVlhgGHLPq+ZAvTyUp55v6xDVphe2LLP3JYBOgB6Awgj/2nWIStML2zZ5zVZgF5eyjPv14aQFQYYtuwzN6dWB0CvliqOOGdDyArTC1v2uUwZoJeL7HZ0ak/ICgMMW/btMGrFPoDeino45ci2kBWmF7bs2z93gF77NbejR9tCVphe2LJvh10r9gH0VtTDKUd2hqwwwLBl3+bpA/TaLLhN3dkZssL0wpZ9m6xb1g3QW6aEs/5rc8gKAwxb9u2cR0CvnWrb1Jf9IStML2zZt8nGv3cD9Nqptk192R+ywvTCln2bbAz02im0nX1xCVlhgGHLvm22hrXXNqnt64hLyArTC1v2bbM00Gub1PZ1xCtkhQGGLfv2GBvotUdn+3rhGLLC9MKWfXvsDfTao7N9vfANWWGAYcu+DSYHem0Q2dYu+IasML2wZd8GqwO9Nohsaxd8Q1aYXtiyb4PVgV4bRLa1C+4hKwwwbNlnbXigl7XCtrYvQsgK0wtb9lnbHuhlrbCt7QsSssIAw5Z9puYHepnKa3fjgoSsML2wZZ/pDAB6mcprd+OChKwwvbBln+kMAHqZymt34+KErDDAsGWf3SQAetlpa3fLQoWsML2wZZ/dPAB62Wlrd8uihawwwLBln9FUAHoZCcuhWdFCVphe2LLPaDYAvYyE5dCsaCErTC9s2Wc0G4BeRsJyaFbAkBUGGLbss5gQQC8LVTm0KWbICtMLW/ZZzAmgl4WqHNoUNmSFAYYt+9SnBdBLXVI+DQobssL0wpZ96jMD6KUuKZ8GRQ5ZYYBhyz7dyQH00tWTW2sih6wwvbBln+78AHrp6smnNcFDVphe2LJPd34AvXT15NOa+CErDDBs2ac4RYBeimJya0r8kBWmF7bsU5wlQC9FMbk1JUXICgMMW/ZpTRSgl5aSPNuRImSF6YUt+7TmCtBLS0lu7cgSssL0wpZ9WnMF6KWlJLd2JApZYYBhyz6V6QL0UpGRZyMShawwvbBln8qMAXqpyMizEblCVhhg2LJvfdIAvdY15NyCXCErTC9s2bc+b4Be6xrybEG6kBWmF7bsW583QK91DXm2IGPICgMMW/YtTh2g16KAnC+XMWSF6YUt+xZnD9BrUUDOl0sassIAw5Z9KxMI6LWiHv9rJQ1ZYXphy76VOQT0WlGP87VSh6wwwLBl3/Q0AnpNS8f/QqlDVphe2LJveiYBvaal43+h1CErTG/ILftJSWqp/c+oa7jjGOiV2M6yh6wwwMG37Puz6n9GYitaGDrQa0E83pfKHrLC9O7YgaKj0caN6N//RufOqWX1Z9X/jPoadxwDvbLa2RkhKwXg5ctRUtL1v4EDUU5OBaP4s+p/psIFrjkAemU1tTNCVkeP+tbb/v3R6NEoMREdPIhefBH164fy8srtgsEmC+Vvu7gE9MpqfGeErI4eRRkZKCUF5eejxo3Rpk3o8mU0ZAiaN6/cLv4rrf+Z8tpuKgG9slrbMSGrv/4VjRyJxoxBERHo8cd95khNRVOnltvFn1X/M+W13VQCemW1tgNCVocPo7feQr16oT590DPPoMOHfbY4dgwlJ6P33iu3iz+r/mfKa7upBPRKaW3ZQ1Y7d6KJE31x5rvuQu+/j4YNQ4MHo48/Rp984isPGYJ++aXcLv6s+p8pr+2mEtArpbXlDVl98gm67z5UowZ64gn0ww/XxT92DP31r+iBB9CAAWjyZFRYKKVR7B800Gu/5hR6lC5ktW8fmjIFNW2K4uPRggXo1181RLh6FZWUaJyHU4EUAHoDKSP0eYlCVmvWoEGDUGSkzx/eulVoVaUbHNArncl8AxY/ZFVQgP7+d99K26QJmj0bnT4tpc6CDxroFdxAGsMTPGT1zTe+xz81a6L770dZWai0VOMW4BQVBYBeKjLa2oiYISvl8c9dd/kiyZMnX3/8Y6su7usM6JXP5qKFrMjHP599hq5ckU9SSUcM9MpnOHFCVpqPf+QTVNoRA73ymY57yErP4x/5ZJVwxECvZEbjG7KCxz9CTRegVyhzhB4Ml5AVPP4JbRgeNYBeHqpb6NPmkBU8/rFgK+aXAr3MJabbgT0hK3j8Q9dqjFoDehkJy6pZ1iErePzDynIM2gV6GYjKrEmmISt4/MPMbqwaBnpZKWui3Q0bfN/M9vXXAS9lEbKCxz8B5Rb+DaBXIBO9/DJS/gKNiW7ICh7/BNJZlvNAryiWunwZ/fnPqKjIt5/u8mXtUVEJWcHjH21xJTwL9IpitE2bfF+G+ttryhTfVytqviyGrODxj6aq8p6Ukl4P8YqIiOjWrduBAwfktYEy8lmzfPvpEEJr1qBZszTuxnTICh7/aKjpiFOy0ovFP3Xq1HPPPdepUyd8RsZCcTEaOLD89wRSUlBxsfo+TISs4PGPWkRnHUtP729f/3v+/Hmv1yu1XbZtQ+np5Xfw/PO+XxhQvQyFrODxj0o9Rx5KT29xcXFGRkb37t2lNs+rr6Jvvim/g/Xr0WuvlR8qJT0hK3j8o1bN0cey0os/+Xq93n79+h1WvslbTlOVlPi+Sob8OsXiYt/v+pBnQn6XFTz+kdP4lkYtK70IoWvXri1evLhNmzZnzpyxpIHYF+fn57/66qsPPDCiatW/ZWfvxL+aqRTg8Y/Y1mM7OonpVYSZN29e//792YrEr/W3314YGRndvPnTf/jDu7GxkyMjG4wfP1XhFh7/8DOLKD1LTy9CqEePHsuWLRNFUXrjyM3NjYys36PHIfzLl3/60+natds8+ujn8OVv9GSWuCUn0Hvo0KFWrVr9qvn9/BKbBt1//4Px8W9hdJVC584bqle/Hb78TWbDUhu7lPRSu3uxG2rYMPbuuw+q6O3T50rVqjcV+z8OFvteYHQsFAB6WahqrM2TJ0/u3Llz1apV8+fPP3jwIL44Li6ha9ftKnp79z5TvXpNXAcKblYA6OVg/ZMnT06ZMmXq1KlTfn/NnTt3xYoVubm5x48fJ0fz1FOpLVqMV9Hbrm1mj7vuJqtB2bUKAL00TU+uolOmTHnNP+XCSG+//PJLdHSjdu0yk5JKFYYTEpZEVo9aPSry6BcvlV6D39szoqYT6zqc3mvXrrVt23bmzJlMbZeVlRV8FTXde0FBwZ13douIiK5bq2Pt2rc1a9YsN/f/rvy85GBm531/+8PFwr2mW4YLHaCAk+ktLS0dNmyYx+MJDw/PyckxZC3VKqo4ul8H+doLQ60brDx27Ni+rSrv3/MPhDbgv9Obn9udWhMWYYNaOqq6Y+ktLS0dNWqUx+OZNGlSfHy81+vVD/D06dMDfRblYvzU1NRHE6uWXFiF0VUKsAhzMYc4nTqT3t+SKOPi4jwez5QpUz788MNZs2Y1bty4UqVKPXv2JMNFFy5cEMcSgUZy6dKltLQ0TXoVhmERDiSd4887hN6TJ0/+9NNP2FqFhYVerzcsLCwnJ6dv375VqlSpVKmSx+OJiYnJyMjYtGmTFNwqt7Nt27a33norCL0IbYBFGJveVQX56N2wYcP8+fOVKBH50GXjxo2k5QoLCxWHee3ate3atfN4PEOHDn3nnXeeeOKJhIQEr9fbpk2bIUOGiA/znDlzNm/eHJxeWIRJ07unLBy9OFxUWFioaYb8/HzVc1HNagih06dPx8fH33jjjR6Pp0uXLu3bty8qKlIqX716dffu3VLAPGnSpLy8PD30wiIcaCY49XxAeq9eRYcOoYMHNb6ihaIWSt4C+VkUh4uo5C3/5z//8Xq9yt79tLQ0EmDyLkSGOTU1VT+9sAiTZnV8WZve3bvRiBHXv2Zp8GC0ZYsZHfAqOn/+fIt5C2a6L7sGr7cIoSAAl1X3/VccmJWQlVF6YREmrengsga9x475viFt/Hi0dSvasQOlpaH+/X3rsJ5XVlYW+VlUMwFQTzvs6ugEmBwAR5iVkJUJemERJi3o1LIGvR98gJKT0c8/X7/lixfRQw9dmzr1lJJGr4SLeOUtUDGDCYDJfu2EWQlZmaaX4iL85ZdfdujQwev1dujQ4auvviIFgTIvBTTonTULjR3rG8+RRx+91eOJi4oa0Pe7ESOO+KfR8xq09X4tAkwOgCnMSsjKCr1UFuFdu3bVq1dv1apV58+fX7NmTXR09K5du0gRoMxFAQ16P/0UDRiAjh1Dvq9F69hxw+3d77/3bJ928wY0ajQxOTn9+eeXLl36448/chkuxU4pAkyOii7MSsjKOr0WF+FBgwYtWLAA3+b8+fMHDRqED6HASwENen/+GQ0ejEaNQqtWoTWfnn38noMDB5QcW7Ft5/Dh02Jinq1a9aX4+BkjRkx4+ulnn302PT1dXpgZAUza0grMOGRFhV4ri3BMTAz5rZ1HjhyJiYkhbxPKXBTQoBchVFCAJky4HnN+/OGL+5vch9atQ3l5vr/16xWM06pWXdS58/4FC1YsWzZjxowJEybICLMNAJN2NQQzDllRpNfcIhweHn6Z+GW0y5cvh4eHk/cFZS4KaNOrDOXcubLY1euvo7Zt0d691wHWwvj/vfVW3j7fa8WKFXLBbDPApJmDwzx79uzNmzfn/f7Sma2hLLB6/jWUHR0TE0N+VsrPz4+OjiZvBMpcFAhGb4UBpaSglJQK9CoM+63GCsbKnJMFZo4AkyKrYA4LC4uNjb3//vsnT57cr3XlX04s1oOl/jr6s6MffPDBefPmIYSmTZv20ksvZWRkDBw4kBw5lLkooJve8+dRq1a+H4fG0PoXKjrVJMbiwywIwOQkmDBhwsqVK19++eUhQ4bUvamS11u5TZvbhgy5JyPjiU2b5l648C/9oAapqWcR3r17d3R09MqVK3fs2NGxY8d69ert3LmTHCqUuSigm16E0IEDqHZttGxZMIADO9UKwOS/oq3MQgF86feNgViuRxOrXj674vfU7ElPPDEgIaGl11uFFsx6FuGcnJz27dt7vd6xY8du3br13nvv5TJfoVNSAW16Vd+ElpRUdsmSJahRI18Glv/Cq3km1GqMZ2denu9TM/fPzOIATIasNKNWV6+uowuznkW4bB4gWHuxFBwLAekNOKbUVNS9O9q/Xy/ARlZjEWAWBGCcZaVoEjJqRQVmPYtwwIkBb9iugHF6S0pQ167oySeN0YtXZiOrMS+YRQAYZ1nppFf1ydYKzIYWYdtnLHRYroBxehFCx4+j+vXR22+bBNjsamwnzNwBxllW5ui1CLP/Irx8+fKoqKgffvihfO5AibcCAelVffRVj3PTJlSnTnkKB15aTRTMrsasYeYI8KWKISvNz70qPg0d6lyZ8SK8d8/uqKioG264ITY29sSJE+rJAMecFAhIb+jxaKZwmKAXX0IDYwVpWgEwXgCrQlbU6VWhHgTmDf+avuyZdjUjwurH1P3oo48iIiJat24NAIemw5YaFuhFyJe/ESiFAzNpokAPY+swcwFYFbJiTW8QmJs1a+DxeMLCKv2xafjjyV3Wr/vK6/VGRESAC20LniE6sUavnhQOE/TiS2hjbA5m+wFWhaxsppeEOTPzqUqVbmjUKDp1fL+6kZVXPtUy8ubqYWFh69atCzGz4G32CgSkN8TnXjwy/SkcmEkTBTYY64fZZoBVISuO9CK0Yd261yMiqjZoULtXr4RaUdXq3lRp04Lx8CtKmACOBW16jQ3IaAqHCXrxJSwxDg6zbQBf8gtZ8aUXoQ0bNswJC6tUqdIN9erV2v/tXPgVJWOAMKtNg16EkLkUDsykiQJ7jP1h7tixY0xMzKJFi8gNN9RN4x+y4k4vQhtuvTUmPPzGr756XfGrcTgaFmHqE0B/g5TotZjCYYJefIldGCswjxo1qkmTJi+88AK7/cz+ISvu9JaUfBURUbWoaDX5kdj/mbD+aQc1qShAiV5aKRyYSRMFuzAeM2ZMXFzc9u3bGeVm+4esuNO7Z887cXG3kujiMizCVDg01wg9ehFCFFM4TNCLL2GPMQmwsib7u9mmv2nEP2TFnd6FC9OGDu2FiVUVYBE2x571q6jSixCinsKBmTRRYIlxIIAtwnxJK2TFnd5x4wZkZDyhglZ1CIuwdRqNtkCbXnYpHCboxZewwVgPwEZh1gxZcac3MTFu48Y3VLj6H8IibBQ/i/UZ0Ms6hQMzaaJAG2OjAIeEeerUqfi7rMjKIXcI+rNE64wSsjp/Pktng7AIW2RS/+UM6DX0LRwmCKRyCT2MrQBM8qnkZnfr1u3hhx8ePXr0448//sYbb6xfv16pw5HeICGrQDzDIqyfQCs12dCLELIzhcMKzzQwpgVwXl7eyJEjs39/rVmzZv78+ampqQrMdzQMW/zRcz/++FkgYNidDx6yCtIvLMJWyNRzLTN6uaRw8MOYCsB79+4dM2aMQq/q39EdqyxfPHnGjEcmTBj47LOD0tOHLl36kj0w6wlZBWIYFmE9EJquw5JejikcPDC2DvDixYunT5+u4lY5fOTOKgf2vJmX94Hyt2/fohUrptsDs86QVSCAEdoAi7BpPoNfyJJeEVI47MXYIsDp6emffvqpHnoxxqxhNhqyCsQwLMLBOTT3LmN6xUnhsAtjKwCPHj1aE93s7GzV2quiV3VIcWU2EbIKBDAswuYQDXIVe3pFS+Fgj7FpgHHIyp9hQ/RShNl0yCoQw7AIB6HR6Fu20CtmCgdLjE0AHCRkZXTtVdGrOjS0MlsJWQUCGBZho5QGqm8XvSKncLDB2CjAQUJWdOk1BLP1kFUghmERDsSk/vN20StFCgdtjA0BHCRkxZTeIDCnpqZUrhz24Yfp7B5NQThaP6v+NW2kV6IUDnoYP9K7d1yrVsp2QjKzyr8cJGRlJ70kzKtWvdy0aQPWj6ZgEfbHUucZe+mVLoWDBsaJYWGNIiJ2ZGTk7dvnDy0+EyRkxYvel18e069fF5JnQ5+ZA/nMmudhEdZJLFnNdnolTeGwhvHDbdrUCw8fX7Xqos6d/X8YNS8vL3jIihe9gwf3nDx5CEmvqkwXZliESTL1lG2nV/YUDrMYp40Z0z42dv2gQdNiYtL8MA4esuJF7x/+0Ozjj19QERvkkArMsAjr4Vapw4NeZ6RwGMfYB3BcXNH27chva0T65MmBsqyys7O/+OKLlHaVd/97ThByqL+1b98ir7fKrl1vmW7ZNMyBFuFffvll//79+ie342tyotdJKRxGMC4HWLmqDOPOYWFvtm+/cfr0tVlZZKrG0qVLu3XrVblyteoRDapUqZaYeMf69a+bxsnQhatWvdysWQNDlwSvbBRmchH+9ttv27RJqFYtqm7dllWr3jRxYlpxcbHj4Qx5g/zodV4Khz6M1QD/ftUzKSlfDRgwpU6dSVWqYIxXr15dr95tzZun9ulzOSkJ9e17rW3b12rUqL1589zgnFB51z9kRaVZ3IgemJVFePHY5jffXCchYYnyCwG9exfddtvAnj37hpzcjq/AlV6npnCEwlgF8KW9e9PGjMnLzs7Lzi744AOM8X31G93W+M+qH7WIi5v6pz/dhRlgVwgZsqLbdRCYYxvfknDHdXQVNfr2vVqvXsfPP//c8XwGv0Gu9Do+hSMwxiTA2xYvfmv6dIVe/G/BBx/E1rqlS5dNKnp79Tpx802R+756nvVffFyDD+cMZd1LoPa/W/vcsgWjpj/bd8xDXapWjVSJkJSE4uP/b/jwR4JPbse/y5tel6RwaGGMAZ6Tnr75008xt7hQt1bDHj0KVBO3b9+rYTdWfqxHw3H33MLub2zPW8JvrPTI3Wx70TP+QZ1ioqrfphIhKQl17Lj67ruTHM9n8BsUgF5XpXBUxFgB+KlhwzCxZKFrQrfbb/9ENXHvuiu3SZM2wY1q/d09e/bExcVZb8d6C8XFxV5v9XvvPavSoUWL9L/8Jd16+1K3IAa9LkzhKMM4bcyYurVqbV+yhORWKb/7yitRkY179y7CE7dPn8v163eZN+9N1nNu4cKFQ4cOZd2LzvYfffTJpk0fTkoqxTp0774/MjI6Pz9fZwtOrSYGvW5N4UB5eZf27r0zPj6uWTNNgJ8YOjKyev3WrV/r1Omrdu3erF271eDBI0tLS1lPx3HjxmVkZLDuRU/7OTk5v/76a6dO3Rs06Na+/fuJif9q2XJKeET1Nxct0HO5s+sIQ69bUziUkNWYlJRAAL+XnNy1dr3ExB4jRjz2z3/+057pmJiYuHHjRnv6CtRLUVHR+PHjv/32W4RQaWnpokWLuve9N6p1g4ceG5b8UXLy2uRAF7rnvEj0ujKFA4esAgH8WtOmRzIz7ZyRJSUlERER58+ft7NTVV/Hjx+fNm3a2bNnyfNfH/06YVlC7qncLSe2NPu02eJDi8l3XVgWjF73pXBMGj0af+L1B/jg8uV/qVwZVZzE+OPfgAFo4kRE/dMfx5DVwYMoPR0NHFj6xhulJ06oecT05p7KfS/vvbrv1z156aS6kpuOxaPXZSkcqSNHYnrzsrNVAO8aNy6zdWvVhEwqe1By+TL6/HM0dqzqfauHvEJWP/6Ihg1DmzZdu3ix9MgR9PzzaO3aCvdC0pt7KnfEhhEu95/Fo9dNKRxklhVmmARY023G9P72rO38efTggxWmuPUDXiGrmTNRVtY1nMB85AhSfWJQ0Qv+s5D0uiaFQzPLCq/AuR984O82I4QwvVeuoKVLfX90X7xCVkOHomPHgt2Kil7wn0Wl1x0pHDhkhRdeXBiTktKyTp0ZLVv6T2f8uVcprFzpX8X8GY4hq/79UUlJsJH70+ty/1lgel2QwkGGrDC3uHB3VFSbhg2LiopUMxqvvSUlaMcONHy46n1LhxxDVsOHI/JeS0vRuXMV7kWTXjf7zwLT64IUDlXICnObl52tRJvTnn66ffv2KoAxvQihy5dRSkqFKW7xgFfICiE0ezbKzi4f/l/SsZMAAA/aSURBVHffqQNymvS62X8Wm15Hp3BohqwwwDjanJaWpgIY06t87n3xxfIZb71kT8iqqKgoKytLNdpDh9DQoWj7dlRcjA4eRI89hnJyKlQJRK9r/Wfh6XVuCkegkJUCMBltVgGMP/f+Fm2eMgX5PxetMOUNHtgQstqyZcvEiRNVmRjKML/9Fk2YgJKT0ejRyD+vLAi97vSfZaDXoSkcQUJW/kkaKoANIqm3ug0hq8zMzAULTKYoB6HXnf6zJPQ6MYUjSMgKu80kdjYAzDRkReYtk/elvxycXhf6z5LQ68QUjiAhK9JtJic3a4DZhayCeMvkDQYvh6TXbf6zPPQ6K4UjSMjK320m5zRTgBmFrPbt22faWybvPSS9bvOfpaLXQSkcQUJWmm4zOYnZAWxDyIq8EaNlPfS6yn+WjV6npHAECVkFcpvJuc4CYBtCVuQtmCjrpNc9/rNs9DolhSNQyCq420zOeOoAMw1ZkSM3XdZJr3v8ZwnpdUQKR6CQVUi3mZz6dAFmF7Iix2ylrJ9el/jPctIreQpHkJCVHreZBIAiwFRCVlu2bNm2bRs5QoplQ/S6wX+Wll6ZUzgChaz0u80kErQAth6yspKJQd5RoLIhet3gP8tMr7QpHIFCVobcZnKKWwfYYsjKeiYGeTuBykbpdbz/LDO90qZwBApZGXWbyVluEWArISsqmRjkvQQqm6DX2f6z5PTKmcKhGbIy5zaTE90KwKZDVqy9ZfIGTdDrbP9ZfnplS+EIFLIy7TaT89s0wOZCVllZWcr3LZNjYFc2R6+D/WdH0CtVCkegkJUVt5kExhzA1kNW5BgYlU3T61T/2RH0SpXCoRmysu42k8AYBdhiyIrsmmnZNL1O9Z+dQq88KRyaISsqbjNJjiGArYSsyE5Zl63Q60j/2UH0SpLCoRmyouU2k/zoB9h0yIrszoayRXqd5z87i17hUzg0Q1Z03WaSIp0A6wlZZWZmHj9+nGzc/rJFep3nPzuOXrFTODRDVtTdZpIrPQAHD1nZk4lBjjlQ2Tq9DvOfHUev2CkcmiErFm4zCUBwgIOHrGzLxCAHHKhMhV4n+c9OpFfgFA7/kBU7t5lkIAjAQUJWdmZikKMNVKZCr5P8Z4fSK2oKh3/IiqnbTGIQCGDNkJU43jJ5C7TodYz/7Fx6xUvh0AxZsXabydmvCbBmyOqzzz7T/L5lsjX7yxTpdYb/7Fx6xUvh8A9Z2eM2k5j5Axw8ZEVey71MkV5n+M+OplewFA7/kJVtbjMJHga4pKQkLi6ucuXK58+fJysIW6ZLrwP8Z6fTK1IKh3/Iyk63mWRSAXjgwIEej+eGG27IUf1eEFlVpDJ1emX3n11ArzApHKqQlf1uMybx2rVrbdu29Xg899xzT40aNbxerxQAU6dXdv/ZHfQKkMLhH7Li4jYjhEpKSlq2bOnxeLp27Vq7du3/+Z//adeuXVhY2MyZMzHeYhZY0Cu1/+wOegVI4fAPWfFymw8fPuz1esPDw+fMmdOqVavs7OyHHnrI4/H06tVLTGjxqBjRK6//7Bp6eadwqEJWHN1mhFBhYWGDBg3Cw8PXrl07YsQIj8fzwgsvYEiELTCiV17/2U30ck3hUIWseLnNCCElE2PdunXx8fE33nijx+N56aWXhCWWHBg7eiX1n11GL78UDlXIipfbTOYtFxQUeL3enj17koSIXGZKr4z+s8vo5ZTCoQpZcXSbV6xYQfJZVFREHgpeZkqvjP6z++jlkcKhCllxdJvN8ekpe/32Ublz587ff/+9uXYsXsWaXun8Z1fSa3sKhypkxcttNg2Px3N9nly5cuXNN9/s0qWL6aasXGgDvXL5z26l194UDjJkxdFtNk0Ophch9Ouvv950002mm7JyoQ30yuU/u5heG1M4yJCVdG4zQgjTe+HChdmzZ3ft2tUKhKavtYdeifxnF9NrVwqHKmRlj9u8ZcsWirlTZR97PVWqVOnUqZODP/fmnsrNPZUri//sbnptSeEgQ1b2uM3UvxMDr72ml00qF9q29sriP7ueXvYpHGTIirXbzOg7MVxIrxT+M9DrS9tHXbuiJ59EeXks/siQFVO3mczEoLLW4UbcSa/4/jPQ+/sUPX4c1a+P3n6bBb04ZMXUbabuLWN0yagVedL+sp2es/IB+L289+q+X/fkpZP236yeHoHeMpU2bUJ16qB16+gCTIas2LnNFy5c2LVrV9mdOPa/9tMruP8M9BJz/fXXUdu2aO9eigCTISumbjNxG44tcqFXZP8Z6K0411NSUEoKRXpxyIqp21zxHhx7xIVekePPQG/FuU47hQOHrNi5zRVvwMlHvOgV1n8Gev2m+4EDqHZttGwZlRUYh6wous0lJSV+g3bFCY70iuk/A71a837JEtSoEdqxwyLAOGRF0W3OzMxcunSp1qCdf44jvWL6z0BvgEmfmoq6d0f791sBGIesqLjNjDIxAty/iKf50iug/wz0BpimNFI4cMjKutvMLhMjwP2LeJo7vaL5z0Bv4GlqOYVDCVlZd5uZZmIEvn/h3uFOr2j+M9AbdI5aS+FQQlZW3GbwlknziECvUP4z0EtOD62y2RQOHLKy4jYfP35cwN/y05LJjnOC0CuO/wz06ph2plI4lJCVdbdZx/jcUkUQesXxn4FeHVPfVAqHErKy4jbrGJm7qohDryD+M9CrDwDjKRxKyMqK26xvZC6qJRS9IvjPQK/u2W8whSN15EijbrMsv6OrWzLKFYWiVwT/Geg1MsN0p3AoISv9brMSW/7hhx+MjMZ1dUWjl7v/DPQaYUB3CocSstLpNkMmhk4bCEgvX/8Z6NU5c8qq6UvhmJOevvXdd/9SuTI6e7bsSu3/QiaGti5aZwWkl6//DPRqTZPg53SkcEwaPTqk2wyZGMFl9n9XTHo5+s9Ar/8k0XEmVApH6siRwd3m7du3T5w4ETIxdGhdXkVYenn5z0Bv+eQwVgqcwnFp797nhg8P7jafOnXKWHdQGyFh6eXlPwO9ZrEInMKxbfHiuUlJma1bm20artNWQGR6ufjPQK/2RNF1NkAKx5z09BdvvfVIZqauRqCSbgUEp9d+/xno1T13NCtqpXCkhXKbNVuCkyEVEJxe+/1noDfknAlVwS+FY2xiIuk2FxUVXbx4MVQr8H5oBcSn12b/GegNPWlC1ChL4Ti8YcPHr746bfz4hOrVD736qnKVkolx7ty5EI3A2zoUkIJexX/++MDHa9asmTlz5vvvv19QUKDj5sxUAXrNqKa+5vjxjMgakdVqxTYd1Dz2ubo1Ehs2aLpt2zbIxFALZe1YCnpzT+VOWzmtckxkw1u6tWiRFhs77Oabo6dPn2Ht1rWvBnq1dTF0dvny5bVrxPbs+d+kJKT8dey4ulq1Gjk5OYbagcrBFZCC3q8Lvq5Vt8HtHT7Ck+Gee45GR9++cOG7we/OxLtArwnR1Jc0atSiS5fN2FpKoUWLZ1NT09RV4diCAlLQO27yk02ajlJNhj/+8fuaNWPIW9+yBfXv7/t//QMPoJ07yXcMlIFeA2JpVv35558jImomJZWqDNa58/qEhD9qXgInzSkgBb2J3XskJCxXTYakJFSzZuP//ve/yo1v2YL+93/Rli2+o2++8f32znffmZEE6DWjGnnN2bNnq1WL8qe3U6cvExN7kDWhbFEBKejt0vOeO+5Y6k9vjRq3/PTTT4oC/fujrVvLxfjmG2TuC/aB3nIRTZeaNm3TqdM6lcGaN38qLW2y6TbhQn8FpKD3yb8+1ei2h1ST4a67dtap0xDfUVISLloqAL2W5FMuzsrKqlWraffu+7HNOnT4uE6dhmfOnKHQOjRRpoD49H6W/1nch3HV6tSMj1+AJ0OPHgV16rT+5JNPy+7D93EXv3A1fEZ/AejVr1WwmgsXvhsVFd2kyf0tWoxr2LBT8+bt9uzZE+wCeM+4AiLT++8T/x63aVytRbXeOfDOgQMH2rXrWK9ehxYtxjVt2j8yMjozcy55uyS9ynn/M2T9QGWgN5Ayhs8XFRWtXLly7ty5GzduvHLliuHr4YJQCghL72f5n7X5vE2vL3r9dOH6J9urV69u3bp17ty5y5cvP3HihOrOVJ97lfizqo6eQ6BXj0pQRwgFBKSXXHL1a6TEnJXA1dat5fFn/S0oNYFeo4pBfW4KiEav/5KrXxr8vLd//+uPjvRfi2sCvVgKKIiugDj0mltyqesL9FKXFBpkpYAg9FpZculKA/RS0BMH/ZOSfOlv5IN4Cq1DE2UKcKdXkCW3TA8E9GIpzBfIcD8ZkDDfIlyppQBfesVZcrE2QC+WwnyBpBchXxCif3/zrcGVgRTgRa9oSy7WB+jFUpgvqOhFqEIyjfl24cqKCnChV8AlF6sC9GIpzBeAXvPaGbnSZnqFXXKxZkAvlsJ8Aeg1r52RK+2kV+QlF2sG9GIpzBdU9MLnXvNSBr3SHnrFX3KxSEAvlsJ8gaTXSuKb+RG440ob6JViycXWBnqxFOYLque9yncmmG8OrgygAFN6JVpysTxAL5YCCqIrwI5euZZcbCegF0sBBdEVYEGvjEsuthPQi6WAgugKUKdX0iUX2wnoxVJAQXQFKNIr9ZKL7QT0YimgILoCtOiVfcnFdgJ6sRRQEF0B6/Q6Y8nFdgJ6sRRQEF0Bi/Q6ZsnFdgJ6sRRQEF0B0/Q6bMnFdgJ6sRRQEF0Bc/Q6b8nFdgJ6sRRQEF0Bo/Q6dcnFdgJ6sRRQEF0BQ/Q6eMnFdgJ6sRRQEF0BnfQ6fsnFdgJ6sRRQEF0BPfS6YcnFdgJ6sRRQEF2B4PS6Z8nFdgJ6sRRQEF2BIPS6asnFdgJ6sRRQEF0BTXpduORiOwG9WAooiK6AP73uXHKxnYBeLAUUhFZgxw707Isnez267ZU3j238z243L7nYTkAvlgIK4irwySe+r8geMuLSn0btHvDAtZTBl+IX9SB/L1fcobMcGdDLUl1om4YChYWoXz/0xhtoQ+E3dyy945EV0+4dcPax9AIabcvdBtArt/3cMPp//cu38J45g1b/uDpiYUSvL3r9/Y3zQ4a44dZD3CPQG0IgeJu7Al9+6aP3xAl0/NfjM3bNQMi3Dg8fXmFc5Nd6kl/QW6GS4w6AXseZ1HE3dOIESk5Gf/sbunTJd2/ff+87zMyscJ/uIZa8baCXVAPKgiqQleX7WcaUFDRqlG8dHjsWnTtXYahAbwU54AAUEEqB/Hz0zjsoIwP985+ouFg9NKBXrQgcgwKyKEB+7pVlzNbHCZ6zdQ2hBf4KwNrL3wYwAlDAnAJArznd4CpQgL8CQC9/G8AIQAFzCgC95nSDq0ABUICPAhC14qM79AoKWFcA6LWuIbQACvBRAOjlozv0CgpYVwDota4htAAK8FEA6OWjO/QKClhXAOi1riG0AArwUQDo5aM79AoKWFfg/wPJqyZb5BykdwAAAABJRU5ErkJggg==[/img][br][br][/*][*][i][i][i][b][i][b] [/b][/i][/b][/i][b]PQRΔ[/b][/i][b]∼PSZΔ:[/b][/i] [br]Hasonlóan: mivel az [i]HACΔ [/i]és[i] AJEΔ[/i] középvonalai[i] QS [/i]ill.[i] RZ,[/i] a P középpontú α szögű és [i]PR/PQ=AC/AB= AJ/AH[/i] arányú forgatva nyújtás az [i]QS [/i]szakaszt [i]RZ[/i]-be, így[i] PS-t PZ[/i]-be viszi át, tehát [i]PQRΔ∼PSZΔ[/i]. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUgAAAFkCAIAAADNGDUpAAAgAElEQVR4Ae2dCXxM1/fAp0ol0to1Skt/VbXvRfFvVSlaza8qhEZQVapobW0pbVW1FLWl1tZWrVpqp2IpEkKUSCwhVBJCZJUEWSaznv/vGW7evHnz5s3MW+ed+cyHe++77977zr3f3DPnnXeeDvCDEkAJ+JwEdD53RXhBKAGUACDYuAiYEkhOTv7kkwkdOnTr2bNPePhPJpOJWQPzipcAgq34KZJ2gFu2bK1UKbBRo287dPi7bdttdev+t3Hj1rdv35Z2FNibtxJAsL2VoC+df+PGjcqVAzt3Ph8UBOTbsOFn77wzwJcuUwvXgmBrYZb5XuPs2XNeeGEsQdqW6NXLEBBQNS8vj28rWE8BEkCwFTAJihlCnz4DW7f+nQF2UBDUqdM5KirK2TCDgpwdwXLZJIBgyyZ6BXY8ceKkxo1/cAS7WrV6SUlJzgaMYDuTjIzlCLaMwldc14cPH65evcGbbxbT2W7fPuKZZ+pzjBXB5hCOXIcQbLkkr9B+Q0OHPvPM6127XrOx/eKLf1aqVPPYsWMcw0WwOYQj1yEEWy7JK7Rfi8Xyww9z/f2r+/vXKl/+CT+/didPnuYeK4LNLR9ZjiLYsohd6Z0GB8OsWelXrxZ07AhbtrgYLYLtQkByHEaw5ZC64vt89lmIjob0dFi+HF57jWW4w4ZBYSFVbjJBcDBLBSySVwIItrzyV2Lvt29DxYpw6xYFdmoqBAbC5cvMcX7+Ofz5JxQXw+7d8OmnzKOYl10CCLbsU6C4ARw4AJ06UVTbvmPHwrhxzEGmpFCFwcHUvykpzKOYl10CCLbsU6C4AcyaBSNHloJ9+jRUq0ZtzvhRkQQQbBVNlkRDDQ6GpUtLwU5Ph549YdUqiXrHbgSRAIItiBh9qhFiOSPa+Pr10KaNT12jz18Mgu3zU+zeBdItZwTstDR49lk4dcq9prC2jBJAsGUUvhK7ZljOCNtffgnvvafEAeOYWCWAYLOKRbuFDMsZATshASpXBnx2Uy0rA8FWy0xJNE5Hyxlhu18/mD9fomFgN15KAMH2UoC+drqj5YyAvWsX1K8PVquvXbJPXg+C7ZPT6uFFsVrOCNjp6dCsGRw86GHjeJqUEkCwpZS20vtyZjkjbM+ZA++8o/SrwPEBYPhhXAU0CTiznBGwr16FqlUhLY12DiYVKQHcsRU5LTINisNyRth+/32YNk2m8WG3vCWAYPMWlQYqcljOCNhHjkCtWtTTmvhRsgQQbCXPjqRjc2k5I2zzib4g6dCxMwcJINgOItFqgUvLGQHbWfQFrUpOideNYCtxVmQZk0vLGQHbWfQFWYaNnbJKAMFmFYsWC/lYzgjbrNEXtCg1pV4zgq3UmZF8XHwsZwRsjL4g+fy41yGC7Z68fLU2f8sZYRujLyh5MSDYSp4d6cbG33JGwMboC9JNj/s9Idjuy8wXz+BvOSNgY/QFJS8EBFvJsyPd2NyynBG2MfqCdDPkZk8ItpsC89HqblnOCNgYfUGxywHBVuzUSDcwDyxnhG2MviDdPLnTE4LtjrR8tK4HljMCNkZfUOaiQLCVOS+SjsoDyxkBG6MvSDpVvDtDsHmLyncremY5I2xj9AUFLg0EW4GTIvWQPLOcEbAx+oLUE8ajPwSbh5B8uoo3ljPCNkZfUNoaQbCVNiNSj8cbyxkBG6MvSD1trvpDsF1JyNePe2k5I2xj9AVFrRQEW1HTIcNgvLScEbAx+oIMk+e8SwTbuWy0ccRLyxkBG6MvKGq9INiKmg6pByOI5YywjdEXpJ4/5/0h2M5lo4EjgljOCNgYfUE5SwbBVs5cyDASoSxnhG2MviDDLLJ1iWCzSUUzZUJZzgjYGH1BIWsHwVbIRMgzDKEsZwRsjL4gz0Q69IpgO4hEMwXCWs4I2xh9QQkrCMFWwizIMwZhLWcEbIy+IM902veKYNvLQ0s5wS1nhG2MviD7OkKwZZ8C2QYguOWMgI3RF2Sb1IcdI9gPJaG9/wW3nBGwMfqC7KsJwZZ9CuQZgEiWM8I2Rl+QZ14f9opgP5SExv4XyXJGwMboC/IuKARbXvnL1rt4ljPCNkZfkG12ARBsGYUvZ9fiWc4I2Bh9QcYJRrBlFL6cXYtqOSNsY/QFueYYwZZL8nL2K7bljICN0RfkmmYEWy7Jy9mv2JYzAjZGX5BrmhFsuSQvZ78SWM4I2xh9QZaZRrBlEbvMnUpgOSNgY/QFWSYbwZZF7DJ3Ko3ljLCN0Rekn28EW3qZy9yjZJYzAjZGX5B+yhFs6WUuc4+SWc4I2Bh9QfopR7Cll7nMPUppOSNsY/QFiWcdwZZY4PJ3J6XljICN0RcknngEW2KBy9+dxJYzwjZGX5By7hFsKaUtf1/SW84I2Bh9QcrpR7CllLb8fUlvOSNgY/QFKacfwZZS2vL3JYvljLCN0RckWwEItmSiVkRHsljOCNgYfUGyRYBgSyZqRXQkl+WMsI3RF6RZBwj2Aznr7D+9e/eWZgKk7EVGyxkBG6MvSDPjCDZTzjk5OY0aNbp16xbzgPrz8lrOCNsYfUGCpYRgM4UcHBy8fv16ZqlP5OW1nBGwMfqCBKsJwbYT8u+//x4cHGxX5EMZeS1nBGyMviDBmkKwS4Wcnp7esGHDnJyc0iLfSsluOSNsY/QFsVcWgl0q4TfffHP79u2leVpq165dVapUuXjxIq1MZUklWM4I2Bh9QezVg2A/kPAvv/wyePBgVnFfvHixSpUqjzzySP369bOysljrKL9QIZYzwjZGXxB1zSDYlHivX7/euHHjO3fuOMr64sWLgYGBtWrV+u233wICApo0aaJSthViOSNgY/QFx8UmYAmCTQmzV69e9rexqRwA7Nq167HHHqtZs2Zi4pXVq+HQoUh/f/+AgAA16uQKsZwRsDH6goAYOzaFYDvKpLQkPDy8TJky9evXP38465MA6NXrYsWKVcqWLXvgwIHSSipJKcdyRtjG6AvirR0E24VsDx8+HBAQUK92k1EtoypUCAwIqDVu3CXV/dBWlOWMgI3RF1wsPi8OI9iuhRcZGelX3v/RR8v6+dc8cuTK5s0wcCD88QcYDK7PVUgNpVnOCNsYfUGkFYJg8xLsvEULy5UrN2bq3gWLrACQkwOzZ8MHH8A///A6XfZKSrOcEbAx+oJIawPB5iXYu2C6aribWKjvG2rJzn5wyrlzMGoUfPMNpKfzakTGSkqznBGwMfqCSKsCweYl2BwwpoI+FfTz1xqXLac2bdvHbIbt2ynNfN06KCl5WKq8/xVoOSNsY/QFMdYLgu1aqimH4MSuB2BfyC/pF2rNz7c7Ky8P5s+H99+H6Gi7coVklGk5I2Bj9AUx1gmC7Vqqe8bAX/NNth07FfSzlpvWrC3dtMn5CQnwyScwdSrcuEHKFJFQrOWMsI3RFwRfKAi2a5H+3AH+iTIQsOOyqU27sJDlRIsF9uyBsDBYvRqKi1kqyFKkWMsZARujLwi+MBBsFyK1mOG7xyHpHvUDm3y/XWTasNHpiXfuwKJF8N57cOSI0zpSHlCy5YywjdEXhF0SCLYLeWaeh4UNrQRpW+KftJL+YVa9nuvcK1dg/HiYPBmuXeOqJsExJVvOCNgYfUHYlYBgu5BnYTac3PfAckbHe+ps0/YdLL+06c1ZrbBvHwwaBCtWAKvqTq8sUlrhljMCNkZfEHYBINgu5GkB5nZtw/tYcknYe1aj0cXpAHDvHixdCoMHw8GDYHXxp8B1a+7WUL7ljLCN0RfcnVyO+gg2h3CoQ3qw0DdqevrT6aZ9+1ycTg4nJcFnn8Gnn8LVq6RMioTyLWcEbIy+IOCCQLBdCPMulN7oolOdCvrDiSVDh1vNZhct0A8fOkRt3YsXU9u4NB9VWM4I2xh9QahVgWBzSTLnMmz9xOmOnQr6sVPM7pq+i4rg55+pW2J790qhmavCckbAxugLXMvRnWMINpe04tfA7wO5wI6IN3w42urBL+fr1+GLL2DcOEhM5BqAl8fUYjkjYGP0BS9nnJyOYBNRsCQYPmcMVdyWHTnBHBPDci6foqgoGDoUFi4EtqBMfBpwUUdFljPCNkZfcDGp/A4j2FxyYvicsYK9I8YwdoLnxm69HtasoTTzXbvArZ/rXON+eExFljMCNkZfeDh7Xv2PYDsVH6vPmSPb163690db4uOdtsPnQFoafPUVjBkDCQl8qvOtoy7LGWEboy/wnWDn9RBsp7KxmOHyeacmcTrhm44YJk9x2g7/A8ePw7Bh8OOPkJvL/ySumuqynBGwMfoC16TyO4Zgc8npFpTQAXaWTjHrBw23CGIGKymB33+nHvDeutVbzVx1ljMCNkZf4FqU/I4h2E7l5MznjBXvdfsMX0/3/Jc2YxAZGTB9Onz0EZw9yzjiRlaNljPCNkZfcGOm2aoi2GxSuV/G4XPmyHayUR861JKc7LQ1Dw6cOgXDh8OsWUCCMbnViBotZwRsjL7g1lw7VkawHWVClVjMMK8uXDOUPqrpCDOjZOUOw6zZgm3atmEZjbBxI6WZb9wIJhP7UJ2VqtRyRtjG6AvOZpZPOYLNLiXWpzUZJDOy/+r1IWHWtDT2Br0pzcqCmTNhxAg4fdqNZlRqOSNgY/QFNybboSqC7SCS+wUufc4YVNuySzYabfGJ2Rv1rjQ+HkaOhBkzICPDdUOqtpwRtjH6guuZdlIDwWYXDB+fM0e2GfGJ2Zv2otRspqzlAwfC+vUuXlegassZARujL3i8WBBsdtGtfMUuzpkjw85KGPGJ2Vv3rvT2bZg7l7rjfeKE04ZUbTkjYLuMvhAUxJSAYwmzhjbyCDb7POebTddMbljOCOes8YnZ+/Cu9MIFylPt66+B9Ve92i1nhG3u6AuOGDuWeCdmtZ6NYLPPHHlDACGWf8JZfGL2nrwoNZth507Kz3ztWmAEYFO75YyAffo0BAbCsWPU25QcH2J3xNixxAsBq/hUBJt98nj6nLHSzhGfmL0z70rz82HBAuopsaNHHzTkG5YzG9vbt0NQ0INvv35UeCn6xxFjxxJ6fe2kEWyWuS7MY49zxooxayF3fGKWLr0uSkyEsWNhyhRITQXfsJylp1O7dO/e1MsPX3qJCik1fTq8/TZcuVIqLMI8PVF6WMMpBJtl8vk8rcnKMynkE5+YpWPviiwWKipLWBj06UPBQLRZ9SYWLoSQEEhKgrp1qdcnlZRQV7dkSamYHPdnx5LS2lpKIdjM2eb5tCZh2FmCT3xiZt9C5O/dg5YtoX172LxZ9Wx//TX1RrThw6FCBejbl5LOxInU603JxxFjxxJSWVMJBJs53R74nLGyzT8+MXMEXueffZZyQR05knrLb0yMKvG+cQN++QW6d4devajQrnFxVAjnjAwIDoZffy0VkCPGjiWltbWUQrCZs+2Zzxkr227FJ2aOw9M8sZzdugWbNkG/ftRjJFevqgbvuDiYMIGyhL/yCvVy4sGDKYecP/6ADz+k0mFhdmGkHDF2LPFUkOo+D8Fmzt/x+dYDK1he/cGKLnehB/GJmaNxP8+wnCUlwezZlB67YQPcuqVovDdsgDffhCpVqPvzFy8+uPKMDOpefZ8+8N//Um8yZb1p776QfP8MBJs5x249rckNtmfxiZkDcjPP6nN28iSMHk1tetHRimP70iWYNg3q1YMWLah3IRUVsVyw2UzhjR/+EkCwmbLieEOAS4wdK3gcn5g5LN55Dp+zP/+kjMzffUfdMVKCqXzvXhgwACpVohRsl5Fep03jLQKsCIBgM1eBNz5njmCngt6b+MTMwfHIc/ucJSfD/PmUCWrdOkqtlQXvlBQqrluLFvDcc5TT++3bPK4KqB8UrJs5r5O1VwnBtpvzvBS4cqP0HfesoLpb6GV8YrvxucoQyxk3sbGxlDfLBx9AZKSkbB89St27qlqV+sEcEeHei1D+ZwgkP7xdiQGP445tvwY8e1qTG3VB4hPbD9NpjmE548Z7xw7o35+6LZyYKC7etntXr7xC2bqnToUbN5yOn+PAzZu8HkTnaEFTh3DHtptu733OWCEXKj6x3VjZMqyWMw68r12DRYsom/Pq1XDzpvB40+9dbdoEfN46zHZZWOa2BBDsUpEJ5XPmyLaA8YlLh8uW4rCcceAdH095dL33Hhw6JBjbrPeu2IaMZaJIAMEuFatQPmeOYKeCXtj4xKWDtk9xW8442E5Phz17IDQUvvySehsJd02Oo3zuXdkPGXOiSADBLhVr2j/w1yxer/5gRZe7UIz4xKVDv5/iaTnjwDI1lfLc7NOHetHvjRvu4e3WvSvGyDEruAQQ7FKRuvWGAG6MWY+KEZ+4dPQg2NOa587BpEmU/+b+/a7Z9uzeFX3YmBZDAgh2qVSF9TlzZFu8+MS2a3DXcsaxdaenU1QPGgSTJ8P58+x4e3PvqlTomBJHAgh2qVyF9TlzBDsV9KLGJ/bMcsaB940blI9nnz6Ufp6a+gBvQe5dlQodU+JIAMF+INc7N+DkVjMrjQIWihqf2BvLGQfeCQmURS00lHJWI89dyXLvKjUVzpwRhwOfaxXBfjClAj6tyf2HQKT4xN5bzjjY3rABXn4ZypeHdu0oZzW5PpmZlO6AHz4SQLAfSEkMnzNWwj2LTxwZSQX0i4pyOqdu+ZxxMEw/xLh3de8ebN9OPR29bh0VpUiWDz18iiwDUEunCPaDmRLJ54yVbQ/iE8+cSb2+a+ZMp+tKWMsZx72rvDzqMZL336eeAJX+g8948ZQ5gk0JSjyfM1aw3Y1PXFIC774LubnUQ47OtkpBLGf8710lJMAnn3ju+M1zdTpWQ7AdZcJagmBTYjEUwsF5olvO6JC7FZ84OpqKvPu/z7RpTvdJLy1nHty7slgoZ7WwMMrPvLiYdXUJX4hg85Spr4Gto30CAgI6d+58+fJlPrLw5g0BdGJ5pt2KTzxnDvWQIwAVXXjOHJar8dhy5v29qzt3qMdI3nsPjhxhGZjgRfhUNk+R+iDY5MpzcnImT57coUMHUuIsIbbPGSvtPOMTGwxUQEISED8khOU9mx5YzoR97urKFRg/nvJmuXbNmYyFKcensnnK0ZfB/l8Y6oKCAn9/f5eyENvnjBVsnvGJT56kbiOTz5Qp1PsxGB+3LGciPXdltcK+fZSz2ooVUFjIGKBg2fh4OH1asNZ8uCFfBttgMCxcuLBLly7c82cxw/YxlutWT96tyUos/0I+8YnnzSt9KRcApfHOn8+8ID6WM8a9K5HCDN27R91qHjyYesmW1cocJ+Ylk4APgk1+Zfv7+7/99ts3XAXsEPVpTW7IXcYnNpmoWEImU+l6MBiokEb0EgDgtpxx3LsqbVfQVFISfPYZFej/6lVB28XGeEvAB8Gmbl9ZLJs3b27atGleXp5LUUjmc8YK+dgpZo/NTklJSfPmzevTZ6if3/f798fRfUvS04H/vSuXIvKswqFD1Na9eDHL6289axDP4i8B3wTbdv1Llizp3bu3S1lI5nPGCrbH8YlXrlxdqVLgCy+Ma9lyTf36UytVqj127Dc2tj24d+VSSp5VKCqiHu0OC6Ps+aiZeyZDz87yZbABoGvXrtu2beMWjZQ+Z6xsexCfODY2tlKlWl27JhNreY8et6tXb/rhh396GTOQW1aeHb1+Hb74AsaNo6Im4kcaCfg42MnJyY0aNSritBSd329OLpLBckYg9yA+8X//279Fi18I1bZEx46RTzzRWpbnrvgs1qgoGDoUFi60e/kWnxOxjgcS8DWwPRCB4G8IIMTyTHgQn/jpp+u/9tpVBti9ehn9/B43GAweCEGaU/R6WLOG0sx37QKzWZo+NdoLgg0S+5yx0u4sPnF2dnZcXNyuXbuWLl16lWZibty47csvn2KA3bNn3hNPVFX+Qk5Lg6++ot68l5DgyWCLiiA725MTNXWO1sGWxefMkW0Snzg7O3vatGnffPPNtPufxYsX79ixIzY2NjMzk74uP/lkYoMGYxlgN28W3vWV1+jVlJw+fhyGDaPe9ZOb694w8alsPvLSOth/DrKev1ziSJrgJXHZN/fGnVy1a8t3SxeNmzb1q/lzGF24FZ/4zp07gYF1mjcPDwqy2vBu23ZLpScq7x5WKf2vb60W2o1vPqtApjolJfD779QD3lu3uqeZ41PZLmdMu2BbLJamTZv1KD876Z6IlrNfI3aOmzZ13LSpMxYv+GXH5r9iT5zJTGUgbcu6G584JSWlffvOlSs//Uxgu+rV//P888/Hxv5szN9yNbzjpe9bFqeddzn3CqmQkUE9u/bRR3D2LN8R4TNeLiWlUbCtVuvgwYN1Ot2jj5Rbf/AvVtKcFTL23nHTpo7/5svNUQed1SflN0BfDJYb8ODvyE0oMYOVHE0F/Zodxh9mu5wyuwppaWkrgh9PPLccIJJ8bx+ffHZiVRVt3QBw6hTlYzdrFq/fzwi23SJgy2gRbKvVOmzYMJ1ON+SNz+tUaeHn78+f7U+/+8a29+5xvvfSWaWnjWDtCwnG+zBngOEOmN6Ac4TtdChJ0BfXCctvnXZ+IFy6CHwfpDg7voqpcBeh2pZQ49ZtNMLGjZRmvnEj02eWsXQRbIZAHLOaA/t/3qaNGzfW6XTTpk2b//rlSUG7a9etU6ZMmf/r9ppt77VpzomFt+lMCpIGgDYQC0DZ4a+DPhQu2bK2xgvB/DVc+2hj/pxFlnBImwzJjrPFWsIKtg1vNW7dWVlUBKgRI7ie4sKnsllXAr3Q98HOzs6+efMmuea0tDR/f/+yZcsePHjw7R7vVir/VJkyZXQ63ZM1a05bOHdr9GExkE4FvY3qNhBrg7kbnNsJOXSwjWDtAwk3Co39Qq0Xsg39gO+9IA6wASLVuHUDQHw8jBwJM2awvzoXn8om69lZwqfAjoyMXLp0qe1GEf2O0bFjx+jXn5aW1qJFC39//wMHDjRv3lyn0/UZFDp31fIhYz5q0baNn79/g6ZN3gl7V3DOyY6dBiXZQLmR0MG2ArwMcSawLlhrXLzc2gni6GPmSHODrd6t22ymrOUDB8L69czYEidPUs7n9E9SUlKPHj0qVKhQtWrV4cOHFxQU0I9qMK0msIm3RlpaGutUJSUlMe73slYDgNu3b7do0eLRRx/V6XSdOnVq1qrludx0m0qcYi7cd/YfMTink5wGVPxeOtgA0BaocPgX8ktCQ6F1fryzwTPK+YCt3q379m2YO5e6433iROl1FxdbunbtnpSURIrat28/d+7cgoKCrKysUaNGjRw5khzSZsITsM1mSE6mHrUV1XnR5qrB6q3B7fvNcyKvXbvm7+9vC8Pw+aRJdLbpv6gF5NyRZDrYFrB2hbMGsNwE/eLl1hfWXud5ITzBVu/WTf2xu0B5qn39NaSlgdVq7du3r06ne+aZZ3Iferf4+fmRXbqkpKRqVRV44PGcX8+quQ322bOUK7/NKWLgQLu/o/xHQPbepUuXzncMCMK/Ie9qkmUBABxsC8U5N9hGsIbAxXQwZILhQrbhmdA7PAMMuQW2erdusxl27oSwMOurr47Q6XTvvvuun59fq1atbJPYu3fvjz76aPXq1TxjV3q3cFRwtntgZ2RQgfXGjoWYGMpoOWkS9O5N7d58PhEREfTfvayeknzaEa8OT7Y95twK0B7O5IIxDShfNwbn98D8A6T+AunFYFkGt3ouyt24kde1ugu2erdui8XSunU7nU7XosXU/fth//79fn5+tWrVunbt2u3bt0eMGNGqVasyZco0atQoLo6vhYKXiFVYyT2wf/sNgoMhP//BhRYXQ2io5ZtvcmxPKdisVlEc76FRvIA8YJs/59mFd7+A5E4QZwVwBDsDDBegqDdcaA9n+kBCdJp+QJhVT+Hv4uMZ2AJu3X///XebNm38/f3btGlz6NAhF8P14vD27dt1Ol31yjVnNs99o6719m3rm2++qdPp+vfvT1rNy8ubOXNms2bNSIk2E+6BPWcOjBp1X1ATJ37/6KPTWrce3C/pwxHZjk8pqFeaXrLNzXnjpk3CwsKIvR3uE05OyQCD6X6gESNY06GEZ3xij8EWZOuOj49/6qmndu3aVVBQsHfv3sDAwPh4vmY/txZJQQb8PQVCKq0pV8avZtWWSxbnjBhB6eSj7q/IKlWqkN/Yd+/e9fPzc6tx36vsHtgbN8I779y/tWgyQbt2d14J6t+rYPmLv1DegIcOuefIr2BZCsg2gTYV9O7a4XjGJ/YSbC+37gEDBqxYsYJM5tKlSwcMGECyQiWMYE38x7x5nOn85ZIfft7z6KN+1apV1+l0U6dOtXUxYsSIqVOnXrt2LS8v74svvujRo4dQXau0HffAzs+n7isOG0Y9KL93492PXr/a7x1Txo6TVEzKVq2genWfIVwktt3lnE98Yu/B9mbrrlmzJj0O7K1bt2rWrCkIDEU5cGqZtdBqzgIDkVuKWf/Bx+bPP1+h0+l69uxJOiooKPjggw+qVq3q7+8fFBSUnp5ODmkz4R7YAFTsy/HjH1jFP3qvOPG5N+HwYbhyhfoeOeJLhEvANlmvzvbzbv+d2L7DhaNHjxc6N5ELBbZnW3e5cuVKaC8KLCkpKVeunJcs3YyBrYNgZmX4Y6iZ8ezd6l2GKfdfn7B9+9+//uplP758uttg24Rx795DE9qCBdCsGZw//4Bt3yJcYrZZOW/xYkTDhiP9/f2bNm0aFha2cOHC6OhoOucCgu3B1l2zZs3U1FSCSFJSUmBgIMl6kNjxoXXBC9a9803/5jKfk0+4ow8JsxL/YHwqm0O8HoJt12JICISE2IFtw9sn9nAZ2bZxbotPbDKZz549u2rVqjFjxrRt25bO+dr+T9zJ2mxjUqh/+XuY9+/ff8mSJQAwY8aMb7/9duHChf369bNbHjwyxmKwgPUemNLBcCWHyTP5e/ftItPqNaXN4TNepbJwSAkBdkEBNGpEPZJDeHZMqFlLl51tx/jEZnMp500Cy/r7P9a06X/Cwl5fuHBMdPTiwsJ9ghDO51ZzP4sAACAASURBVOGws2fPBgYG7ty58/Tp0+3atXvqqaf430M2GyFhE6zuDL/2Ln1MnWDMSBy5XDJoqN39PwTbAefSAiHABoDLlynL2bZtXGyrWUuXl23u+MRnx1cpubvj/nb++Zgx77Rt29Dfv7xQnPPZug8ePNiqVSt/f/9Ro0bFxMS88cYbpevLScpspO5dzakJv3S1RG0xXjO5CGJz3ar/cLw5MtKuOQTbThz2GbfBZgTQCwp62N6WLVCnDuWP5rhds5aobQ+XkW3u+MSOv7HN5sPCcs5n6364DsDljm0Eaz6Y9syi7l0xtmVn2V8jDJ9PJj08SOBT2UyJ0PKegE073T45cSJ06UK97oGVZGeF6iFcRradxScGAEewGXq4IJzz2brtV4NdrigHoudar0Rb6PeunGHMKL90T99/kOW6w0Mx+FS2nYjtM4KCbTLByy/Dxx+7BzYBXg2Ey8U2iU9sP31UziXYAnLu1tZtGyr93tW5S3y3aDrb3y8xrfiZ5ZW8jk9lOwpHsyWCgg0AmZlQqxasXOkh2zbIlU24XGw7i0/sLthecu64dW/fvr1y5coXL150pOjiPqf3rujocqSPJpWEDrayvqMpNxc0/6yHo8gflHgCNuNnNrPt6GioUaPUa4VsyB4klEq4LGw7i0/sJdiecU627vPnzlauXPmRRx6pX79+VlYWAOSllN67um5xYRXjQDoV9Net+lGfmf/+m7nEMO9SAp6A7bJRYPVa8QBscoryCJeF7ZU7DLNmM5VSYcHmz3nkvu+2fdq8akDZWjWfXL9+fUBAwPNPN1nYMWtOLetVB98SboCdHV1/0DDhMyu+f9c1cQ41xAEbgHJZcea1QnD1IKEkwqVn+1895XrFCAwlKtgcnD//fG2dTle2bJlX65Wb0GrOyKpHHivj71c+4MC5eGegulV+uUjff7CFFv7IYfFigXMJiAY2H68VD8AmpyiDcOnZXrLRuGCR3aYtJdh0zsPDPylT5pE6dQInjn272eOdfx3cpWLFJ8qWLbvh8D63AHZWefbPpiVL7a7U+TLGI0wJeAK2i9/YpAv+XisEVw8SchMuMduJhfq+oRb66yblAhsg8vDhBQEBfrVrV3+1e9uqlSs8+XiZiBWjr1sKnLHKv/z4tZIBg6z37pHFhAn3JOA22O41767Xigdgk1PkI1xituevNS5bXrqVyQg2QGRk5KKyZcuUKfPIk09Vizyz5Hx4x7Pft0hOO82fYdaaYyabIyLcW2tYmy4BkcEGAM+8VgiuHiTkIFxKti/kl/QLtZIAVfKCDRBZ99maZcuV3XBoQSpEpULUleOT4yZWTfzra4+37k2Rhk/Go82MzqnbafHB9tJrxQOwySnSEi4l27OWm9asfbBpywu2yXSoQoDfudw9Nqpt/17L3+rx1n2lWP/ue5bLl3kt5ZISD+Pk8mpdzZXEB1sorxWCqwcJqQiXjO24bGrTtgVfkBfsc+dWNWj8LJ1qkvZs65632rhwkRtI4VPZrMKSBGwAENBrxQOwySniEy4Z298uMm24H59YXrBXr57Ud1B3AjMj4e7WffJmSf8w6507rGuVvRCf8WKVi1RgAwjvtUJw9SAhJuHSsP1PGsWAXu+2rzj9lpX36VGj35m28GMGz4ws/6173JfmXbtL7YKsS5ZRiGAzBGLLSgi2eF4rHoBNThGHcGnYtsUnlnfHbvdS4y3HFjNIpmdvwNFUiOKzdW+NNoz62GqxsC5Up4UINqtopAVbbK8VgqsHCaEJl4BtW3zi2LFPOr743vutmE8LNsvZpYJ9dJLp6RtwtBgKbWynQUzG8cVnJ9ZI/Wt6qsO97qsl+oHDLAl83x1cupjxqexSWdBS0oLtVqwVD+AU5BThCJeA7U+nm5b2CZYLbA7LmQ1vIxT1hQQjFKVBTCYUjYTLQfn79oS/mvB96xT7e92LfjPNneeeEm5bxvhUNg3n0qTkYAOAlF4r3qAuBOFis304saRPs19L7u7ms8EKXofbcpYKUeT9ZEWQPQmStkJmMZj3Qvrm43PjJ1Yn97pPp5eEDLTm5ZWuS/4pfCqbVVZygC2L14p8hIvN9rB28/6OOC44tHwa5Lac2ahuA7G2twV3gbPFYEqDmGLQ94WE4vyr5F73p9NNW7exrk/XhZmZ8PvvrqtprYZMYMvotSIH4aKyvSHslREjrlmtkXxQFLaOS8sZ2bEtYOoM8QYwZUDsHTD+H/VmQrPNTW3dwG6De50yGU1aY0/U65UJbCV4rUhLuHhsx42v8uHHyTExccJC67I1l5YzuipeDLnj4N8DcPs2GD6FpLYQe/+FhFFJhqMDh6TsnjT40vcti9POi7rWNdW4fGArx2tFKsJFYjtufJVth6PHTrjpEkVhK7i0nNHBvgX/3ISiQZDYGeLXQ1YHase2pELU4g2XZv6QDBBJQrJYLbh1C/AnSFawlea1Ij7hYrAdN75KSsHu90ffio+PFRZd7tZcWs7oYKdClAn0Jii2gjkFinrCOTMY4rJOhAzMys5+YCBwjKYmwALXahNyg61MrxUxCRec7bjxVa4V7t505NzkKancKAp7lNtyZrvdZQVreziTC0YT6N+GuMOQdxdMqyBtMiQXQfbkmSmbNl9kjAq3bkH+FikAbCV7rYhDuLBs28BOMR8dNDw9MfEUgxPxsi4tZ6kQVQTZX0ByJzhjBespuPs2XHgZ4iZDUh4U7j1z9v0R6UZjlOMIcev2nm0FgK0KrxWhCReQbRvYqRC1bt/5r6dfc+REjBI+ljPbpl0E2baf01lwzqaKF0H2NdOJISPTT58+wzE23Lq9wVsZYKvIa0U4wicNGNCsZYtzuemsIUT4FxKwk41HQ4dmJCef5KBFqEN8LGd031JGevmWi9NnuP4bxHPrtlrBrQfCvAFGLecqBmzVea0IQfgkf/8W1apd2bE51VzIn2RGTQJ2KkSt3JEwazZlZBb7y8dyxoCZZONzTvQbmJWZeYLnIPls3fhUNuMvjpLAVqnXineET2rfvmUF/5xqVQuGv591KMIDwulg/6s/FhKWlZYWw5MZj6vxsZwRkhmJqXOSf19/ya2uXW7d+IyXgsFWu9eKp4R/Pnx4s/rPp4wbY2jd0lK9mruE08FOhaglGy8tWHTVLWw8qMzHcsbg2Zbdfz72vQ/SDQYWm5nLYXBs3Qi2ssH2Da8V9wmn2G7c6Fz8yVvRh/K/+JQ/4cnGe9uGVLyUvYVQlFgY3Te09OawS1o8qMDfckZGZUukmI++P/qWN05yzrbuyZPvJCYmMha3lrNKUsXJPAj+hiD3SfPqpYIedUfYTr2WmHot0SXh5/My3goJLe/3eLWKtcuXr9DxtU4nrm+28TN/7eVly694QCzPUzy2nK3ckfDVtOs8e+GoRt+6z5w507Rp28ceq1yjRkM/v8cnTJhkMBjIUtJsQpFg+57XCj/UGWxzEP6vPr/Ocw0bNPysV6+SoCB46y1Ls2bzq1R7MjZjeypEXcg/3i80Kz8/moMNbw55Zjm7kH88JCxTqN//tq1786gXKlas0bbtFttLLHr2zP3Pf/p16/aWZnkmF65UsH3Va8UV4axsOxL+eeu29f4zkPFKlsZNpr8Z3NO2ac9afnXN2kRv6OU41zPL2TcLktb+KvCQ6td9pu2LD6i2SeOtt8xPPdXuzz//JEtcmwmlgu3zXivOCedgmxDe7Kl6nTpFM8Du3j2rYsXKSVcWJV1ZdCrm5z5BlzPPLrl3ZaHg3xdbPrvxj7G2jnj+u3/vb+8GX8w+/5OAg0mJ+e6Jx6syhBAUBC1a/DxkyAht8kyuWsFga8RrhY1wl2wHBtbt2jWFsabfesv8WNnHYmd3OPdjx3M/dpzUe+GCsGlXfvw/Yb+X5nTyf+zRmO/b23rh82/83P8Le3nz+tGjhR3JromtnqxSjyGEoCBo1273a68FkSWuzYSywdaU14o94dxsd+7co3XrDYw1/corsXWfa0LcV0h8YmFX9rlz5xo0bkR64ZNY+5dx8lRP4plxj9xgMPj7P/HGG3cZcmjQ4MsvvviS+1yfP6p4sDXotfKQcA621/++ukqVZ3v2zCVrulevkqdqdZqxJJxOmi0+sbCLePXq1X0HhdJ74U5fvKsPCbOkpgo7igetffjhx/XqvRcUZCVy6NIlsVKlwCTNv1Zb8WBr1WvFdr+Ng+1xY8dVqli7SZP5HTocat58WbXqjXoPHHLdWkzHzBaf2GgUEqpRo0dPWziX3gt3esZPxl9WCjkA0tbBgweLioo6dOhSu3bnVq3WvfTSvoYNp5ULeGLZ2hWkjmYTagBbq14rLtmOGDt6xH/qt36pS8jQ4Wv2bGMF7NPppn37hFze7V56acuxQ6x9ORZG/lsycIi1qEjIAQBAbm7u2LFjz5w5AwBWq3Xt2rVd3nqjcpPaoSMHB68PDj4QLHB/KmxOJWD7UqyVh5o2fx8YZ/t2cY9ut39bTceJrEArgAEsGWA4nFgydLjVbCZHvEqYTKYKAQGXCnLonTpLX7fqP5xgPnzYqx4dT87MzJwxY8bdu3fph6LSo9puaxubE3si68TzG5/fnLyZflSDafWArVWvFWf79s0Lpy0VK968m0W4AgDyU/Odd2DCBLiaBBlgGDvFfOSIMGvbLcvZb/sNn00Cq0BWs6tX4csvoV8/608/WbOymJdDwI7Nif31yq9PrnsyW5/NrKSlvKrA1qrXCivbtxfMKX7rTUJ1KuhtYNtWb0kJbP4TRo0CI1gj4g0fjhbmPfL8LWeXCvT9B1uSk4WBKTUVBg+G6GhLcbH11i2YMgUOHLBrmQ52bE7s0MihGlfIVQW2hr1WHNlm1cOD7t++TQX9LSi5VwD9+4MFIBX0IyeYY2LsSPAsw99yNnOZadlygTZrgNmzISLCQpzAb92C8HC7K2CAjQq52sDWsNcKne0L0YcYejhjxzYaYetW2LIV8sGUCvodMYaxEwTAjKfl7FhySehga0GBHXveZAYNgowMrgYYYKNCrkKwNey1QthuXrv2rR6v0/VwAjb5mR0UBDt3Qt59sK9b9e+PtsTHc7Hh8hhPy9l1q37MJPP+/S7bc6NC795g4gw37gi2xhVydYKtYa8VG9uTnn22ed26jHhp9N/YJhOcPg1DhoAZrDb+Nx0xTJ7iBkuOVXlazjYcMoybKJjNzDaMIUMgN7d0RFYr3LtXmgUAVrC1rJCrE2xte63AmTNQseLn48Y1a9WSzjYBOxX0aaDXl0BIyIPf2KmgTzHrBw23eBOMgI/l7HKRfsAQy7//2lHnfWbuXKCrABcuUHZB+ocVbC0r5KoFW8teKz/+CG9RjxwzYhgTsAHAYIQtW63Tp0Mx9SYdve27bp/h6+me/9LmYzmbs9IY/hOdOLfTubm5ERERjNOSk2HQIDh1CgwGuHoVRo6EgwftqjgDW7MKuZrB1qzXyuuvw2+/2dY1nW0b2Lbf2P37w7RpkJFlvQUlBOxkoz50qOe3oFxazmJSSwYMstp7jtjh5zJz4sSJCRMmMJxPbGedOQPjx0NwMHzwAezZw2yJA2xtKuQqB1uDXiv39XCg0cNg27bkLQB6sNCptuG9codh1mxPNm0+lrOxU8x//cVEjn8+PDx8xQoP3bw5wNamQq5+sLXmtfJQD6cDQ2eb7M+siX/1+pAwa1oa/WxeaZeWsz+PGsaMtVosvFpjVKL7fjMO8cxyg61BhVz9YGvNa4Wmh9MXPX+2l2w0Lljk9qbNbTn7V08p+Zcu0UfEN82hfvNtwolVPDYnlny1ppD7BNja8Vpx0MPpS58n24mF+r6hlmw3Pam5LWfz1xrnLXD7j8X/fkhdunTJY/Wbfu0ud2ytKeS+ArZGvFbY9HD6+ubJ9vy1Rnf9PTksZ7ZQLfn59IFIneYDtqYUch8CWwteK070cDpGfNi+kF/SL9TKH0Vuy9nEaebtO+hDkCHNE2ztKOQ+BLbPe61w6uF0mPiwPWu5ac1avsozh+Vs+wnDR2MEe96bfhVupXmCrR2F3LfA9m2vFVd6OJ0El2zHZVObdmEh/SSnaWeWsySDfuAwy/nzTk+U7AB/sDWikPsc2D7stcJDD6eD5JLtbxeZNmykn+E07cxy9tN64w9znJ7FOHDixImTJ08yCoXKugW2FhRyXwTbJ71WeOvhdFS42eYfn5jVchabURIy0Hr7Nr1Dp2lvnE+cNko74BbYWlDIfRRs3/NacUcPpy14pj85w2uFT3xiZ5azz2eY/txC74o97b3zCXu79qXugu3zCrmPgu17Xitu6uH0Zc+xb/OJT8xqOdt92vDBSCv3M9IAIIjzCf1anKU9ANu3FXLfBduXvFY80sPpDHCw7TI+saPlLNmoHzzCEhdH74ElLbb6Te/SA7B9WyH3abB9xmvFUz2cvvSdse0yPrGj5WzpJuN3M13cKouIiLDF/aaPQby0Z2D7sELu62D7hteKF3o4nSVnbHPHJ2ZYzuKyKZuZYwBgekfSpz0G21cVcl8H2we8VrzWw+mYsbLNEZ/Y0XI25Qe+N8no/Yqd9hhsX1XINQC22r1WhNDD6Vyxsu0sPjHDcrbvLPVeEYOB3p4i0t6A7ZMKuTbAVrXXikB6OJ0/R7adxSemW85SzPqhoyz//ENvSSlpL8H2PYVcM2Cr1GtFUD2cTiGDbWfxiemWs5+3GVlDpoWHh2dmZtIblz7tJdi+p5BrCWw1eq0IrYfTkWOwzRqfmFjOzuWW9BtoZUTtl8b5hD5mZ2nvwfYxhVxLYKvRa0UEPZzOBp1tx/jEdMvZVz+a1v1md4tLMucT+oCdpQUB25cUco2BrS6vFdH0cDoedLYZ8YmJ5exgQsmQYdaSktLzpHQ+Ke3VeUoQsH1JIdce2CryWhFTD6czQthmxCe2Wc5SzPoPPjYfP/7gDOWo3/RLEApsn1HINQm2WrxWRNbD6WAQtunxiW2Ws9W7DFO+LK27adMm1rjfpTXkSAkItm8o5JoEWxVeK5Lo4XQGbWyfSs8g8YnbvfTSun1RIWHWmzfpFZWYFhBs31DItQq28r1WpNLD6Zja2J6zMn/eAmPjxo3LPfbY1DmFq9fQqyg0LSzYPqCQaxhshXutSKiH02H9fNKkJi06PF1ngE6ne+SRR7r1OKDX048rNC042GpXyLUNtmK9ViTXwwmvFoulWbNmOp2uUaPQ8n7PlS/vf5Dx/jtSVUkJwcFWu0KuebCV6bUihx4OACaTqWHDhjqdrkOHLuXKHatVe3Xz5s3Lli07e/ZsJVHMMhYxwFa1Qq55sJXptSKTHn7jxg1/f/9y5cotWrToySd/XLYsOjQ0VKfTde/enQUmJRWJBLZ6FXIE+/7y3LIF6tSB06fhyhX5v/Lp4QCQlpZWu3btcuXKHThwYOjQoTqd7quvvlISwuxjEQls9SrkCPbDhTJxInTpAomJ8oMtkx4OADbnk8OHD7do0eLRRx/V6XTffvvtQwEp+n/xwFapQo5gP1yvyvFakUkPp/t+p6Sk+Pv7d+vW7aF0lP6/qGCrUSFHsGlLNjMTatWClSvl3LTl08N37LB7AVdubi5NNEpPigq2GhVyBNt+yUZHQ40acPiwbGzLp4fbC4JvTvfw87+f5R07dkxISOB7pqD1xAZbdQo5gu2wvhYsgGbN4Px5ediWSQ93kALfAp3uwRIyGo3Lli3r1KkT3zMFrScB2OpSyBFstvUVEgIhITKALZ8eziYFXmUEbAAoKip6/PHHeZ0mdCUJwFaXQo5gsy0xubxW1KaHAwABu7CwcO7cuS+//DKbQEUvkwZsFSnkCLaTNXf5MlSvDtu2SbpvS6KHnzhxQkBPsoc/sXXly5fv0KGDD//Gjs2Jjc2JVYtCjmA7AVv6WCuS6OGCRz4hO7ZzOUpxRLIdWy0KOYLNueyk9FoRWQ8XKfKJBsFWhUKOYHOCLaXXiph6ON35hPOC3T6oTbCVr5Aj2K6WsjReK2Lq4YKr33SRaRNs5SvkCDZ9lTpJS+C1IpoeXlhYGB8f7+TCfKdYyt/YNiuawhVyBJvf4hbba0VMPZzfFaq7lixgK1khR7B5L2jxvFbE1MN5X566K8oCtpIVcgSb94IWz2tFND2c97WpvqJcYCtWIUew3VnTInmtCKeHm0wmd67Hd+rKCLYyFXIE283FLXisFeH08PDw8K1bt7p5PT5SXUawlamQI9jur2xhvVaE0MNFcj5xXzSynSEv2ApUyBFs99eisF4rXuvh4jmfuC8a2c6QHWylKeQItkdrUSivFa/1cFGdTzwSjTwnyQ620hRyBNvThSiI14oXejiq3/SZUwLYilLIEWz68nAz7b3Xihd6eGZmpgLfeummBAWrrhCwlaOQI9jerS1vvFa81sO9G7pPna0QsJWjkCPY3q1vb7xWvNDDvRu0D56tHLAVopAj2F6vco+9VrzQw70etK81oCiwlaCQI9hCLHEPvFbc1MMLCgqEGKjPtqEosJWgkCPYAq11d71WeOvhNuv3xYsXBRqobzajNLBlV8gRbIEWurteK/z0cHQ+4Tk9CgRbXoUcwea5cnhU4++1wk8PR+cTHkJ/UEWBYMurkCPY/BcPj5o8vVZc6eHofMJD1nZVlAm2jAo5gm23PgTI8PFa4dTDT506NWHCBHQ+cWsuFAu2XAo5gu3W+uFXmdtrxZUenpOTw68brFUqAcWCLZdCjmCXLg7BUtxeK670cMGGoaWGlAy2LAo5gi3O8ufwWuHUw8UZje+3qnCwpVfIEWzRFj2r14orPVy00fh4wwoHW3qFHMEWc8U7eq3Y6+G5ubnFxcVijkArbSsfbIkVcgRbzKX/0GvlRmTkH/PmzZo4cXfLlsWrVtm6tDmf3Lt3T8wRaKVtVYBtU8j/uPzH3r17Z8+evW7dupSUFJFmCMEWSbAPm83MXFipSqUK1erXG9DghS/qVn3p6dr1Tp48ic4nDwUkzP+qADs2J3bGzhmP1az09DOdGzSYVL/+4IoVA7/7bpYwIrBvBcG2l4fQue3bt1evUr9bt+tBQWD7tmu3u0KFKgcPHhS6K023pwqwo1Kiqj1Zu3Wb9WQxvP56emBg69Wr1wg+eQi24CK1a7BOnQadOh0nE2lLNGjw2cSJk+zqYcY7CagC7NFTP36u3jDGYnj11YSqVWvSr/7ECejdm9oG+vSBuDj6ETfSCLYbwnK3an5+fkBA1aAgK2MuO3Y80rbtq+62hvU5JKAKsF/q0rVt2+2MxRAUBFWr1r1+/brt6k6cgL594cQJKnf0KISEwIULHNft9BCC7VQ03h+4e/duhQqVHcHu0OHvl17q6n372AKRgCrA7tTt9Rdf3OoIdpUqz9y8edN2Lb17Q0wMuSyKbc/eAYFglwpRjFS9ek07dDjMmMsXXvhk0qSpYnSn2TZVAfbHX39S5z+hjMXwyitxNWo8TSYuKIgkvUog2F6Jz+XJERER1arV69IlkUxnmzZ/1KjxdF5enstzsQJ/CSgf7E1Jmxr/3rhCjaotWqwgi6Fr15QaNZps2LCRXCkdbFKNHOWfQLD5y8rDmqtXr6lcOfC55/7boMHop5/u8MILzc+dO+dhW3iaEwkoGex/sv4ZHT262tpqqy6vunz5cvPm7Z56qk2DBqPr1etdqVJgePhi+jXRwbaVO5bQ6ztLI9jOJCNkeW5u7s6dOxcvXnzs2DGj0Shk09jWfQkoFuxNSZua/tm0+1/dbxY++BVtNptjYmIWL168ffv2rKwsxgQyfmPbLOSMOnyyCDYfKWEdpUtAgWDTN2r+4rNZxW32s5iYUgs5/xZsNRFsdyWG9ZUoAaWB7bhR85cauY/du/eD+178zyU1EWwiCkyoWALKAduzjVpw0SPYgosUG5RBAgoB25uNWlipIdjCypPZGrljERRE+QnSfQ+YVTHvhQRkB1shGzURIYJNRCFKgn6vgm4XEaUzDTcqL9jK2ajJEkCwiShESdDBBqBsIb17i9KRxhuVC2ylbdRkGSDYRBSiJBhgA1BP7eBHcAnIArYCN2oiWASbiEKUhCPGjiWidKyxRiUGW7EbNZl2BJuIQpSEI8aOJaJ0rLFGpQRbyRs1mXYEm4hClAQDY/yNLYqUAaQBW/kbNREvgk1EIUqCDrY3HoKiDM6HGpUAbFVs1GRKEWwiClESjPvYtsgYovSk7UZFBVtFGzVZBQg2EQUmVCwB8cBW10ZNphDBJqLAhIolIAbYatyoyRQi2EQUmFCxBAQHW6UbNZlCBJuIAhMqloCAYKt6oyZTiGATUWBCxRIQCmy1b9RkChFsIgpMqFgC3oPtGxs1mUIEm4gCEyqWgJdg+8xGTaYQwSaiwISKJeAx2D62UZMpRLCJKDChYgl4BrbvbdRkChFsIgpMqFgC7oLtqxs1mUIEm4gCEyqWgFtg+/BGTaYQwSaiwISKJcATbJ/fqMkUIthEFJhQsQT4gK2FjZpMIYJNRIEJFUuAG2ztbNRkChFsIgpMqFgCHGBraqMmU4hgE1FgQsUSYAVbgxs1mUIEm4gCEyqWgCPY2tyoyRQi2EQUmFCrBE6fhs+mZ3f/8OQPyzKOXTur5Y2aTCGCTUSBCVVKYMMGKlR72FB9j2Fn3+ljCRmob7G2K/191Kq8Kq8HjWB7LUJsQD4JpKXB22/DTz9BZNrRF7e+OGLHjDfeuTvyyxT5RqSUnhFspcwEjsMDCezbR23XeXmwO3V3wOqA7n91//GngrAwD1rytVMQbF+bUU1dz99/U2BnZUFmUeas+FkA1O49ZIidDOiBYunRoO0q+VwGwfa5KdXSBWVlQXAwfP896PXUZSckUNnwcDsRaAdm+mUj2HRpYFp9EoiIoF5gGhICw4ZRu/eoUXDvnt1VINh24sAMSkAtEkhKglWrYOFC2LMHDAbmqBFspkQwjxLwAQnQf2P7wOXwvARUxXkKCqupVQK4Y6t15nDcKAEOCSDYHMLBQygBtUoAwVbrzOG4UQIcw2YvowAAAGpJREFUEkCwOYSDh1ACKAE1SQCNZ2qaLRwrSoCnBBBsnoLCaigBNUkAwVbTbOFYUQI8JYBg8xQUVkMJqEkCCLaaZgvHihLgKQEEm6egsBpKQE0SQLDVNFs4VpQATwkg2DwFhdVQAmqSwP8DnEWbRRY/K/MAAAAASUVORK5CYII=[/img][br][br][/*][*][i][b]PSZΔ∼XYZΔ:[br][/b][/i]Az előbbi gondolatmenetet folytatva használjuk ki, hogy az[i] FCDΔ[/i] és[i] GHCΔ[/i] középvonalai [i]XP [/i]ill.[i] YS[/i], így XP/YS=FC/GC, és (XP)(SY)[i]∢[i]=[/i]γ[/i] másrészt[i] FGCΔ∼ABCΔ∼PSZΔ, [/i]így ezért a [i]Z[/i] középpontú γ szögű és [i]ZP/ZS[/i] arányú forgatva nyújtás, amely a P pontot S-be, így X-et Y-ba viszi át, vagyis PSZ[i]Δ∼ PSZΔ∼XYZΔ,[/i] így az előzőek alapján ABC[i][i]Δ[i]∼ XYZ[/i][/i]Δ, [/i]és ezt akartuk igazolni.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUgAAAFkCAIAAADNGDUpAAAgAElEQVR4Ae2dB3zTRvvH3UFL4S0UWl5a3rfl/5bSxQtdL+1bOumAvkAoEHaYZUMpq4yyQkvLCHsUaBll71X2KJuGkbAJJJABJMh2lp3heMTW86+k5Czbsi3Jkizb5w+f9nQ6ne6eu2/u0en0Ow3gH7YAtkDYWUATdjXCFcIWwBYADDbuBNgCYWgBDHYYNiquErYABhv3AWyBMLQABjsMGxVXCVsAg437ALZAGFoAgx2GjSquSmlpad98M/zddz/74os28+cvKC0tFZcPvkoNFsBgq6EVgl+GrVu3Va1a85VXfnj33T8aNtxeu3bLV199Mzc3N/glwyUQZQEMtiizhddF9+7de+KJmh99dDUqCtC/l18e2bp1x/CqaATVBoMdQY3trarTp8e9+OIQhDQTaN7cWrly9fz8fG9X4Xg1WwCDrebWUahsbdrEvPnmWjewo6Lguec+OnHihLdCREV5O4Pjg28BDHbw2yDoJRgxYvSrr07zBPvJJ+ukpqZ6Kx4G25tl1BCPwVZDKwS5DEePHn3qqZeaNSths/3OO/uffbauj5JhsH0YJ+inMNhBbwJVFKBz857PPvv5p59mMGz/5z9bqlZ9+tSpUz4Kh8H2YZygn8JgB70JVFCA1eDY4Jg2bcZjjz312GO1Hn308YoV3z57NsF3yTDYvu0T3LMY7ODaXwV3Xw2wsawY0dEwdSpx+3ZRo0awdaufsmGw/RgoqKcx2EE1f9BvzqIaAP7v/+D0aSAIWLIEPvmEo3C9ekFxMRVfWgrR0RwJcJRKLIDBVklDBKMYrlTn5kKVKnD/PgX23btQsyYkJ7uXatQo2LIFSkpg92749lv3s/hYPRbAYKunLZQtiSvVAHDoELz3HkU182/IEBg61L1I6elUZHQ09d/0dPez+Fg9FsBgq6ctFCzJBedzNbrr1KnQv78T7IQEePJJanDGv1C0AAY7FFtNljJHR8OiRU6wCQK++AKWL5flXjhTuS2AwZbbwiGTP5o5Q974unXw1lshU35cULYFMNhsa0RumD1zhsDOyqLmyc+fj1yzhG7NMdih23ZSltxt5gyxPX489Ogh5Y1wXspYAIOtjJ3Vfhe3mTME9vXr8MQTgL/dVHv7eZQPg+1hkvCLWA9Q4KdWnjNniO127WD2bD+X49NqswAGW20tInV5PN5Xc97Ac+YMgb1rF9StCyTJeR2OVKkFMNgqbRhpisWPas6ZMwQ2QUD9+nD4sDQlwrkoYwEMtjJ2DsZd+FHtueaMjTQTjouD1q2DUQV8T7EWwGCLtZzKr+NNNQB4mzlDhN++DdWrQ1aWyuuMi+e0AAbbaYvwCQmhGoBa++225gwhjQJffQWxseFjobCvCQY77Jq4FGCvsEr5mDlDYB87BrVqUV9r4l9IWACDHRLNJGMh/c6cIbb5qC/IWFCctRALYLCFWCsc03pbc4Z4RgFv6gvhaJWQrxMGO+SbMMAK+J05Q2B7U18IsAD4cjksgMGWw6qhlCefmTPENqf6QijVNmLKisEO/aYObE0Yn5kzBDZWXwiV7oLBDpWW8lLO1QCHvJziEc1/5gyxjdUXeNg1+Ekw2MFvA/ElEPi+2vNG/GfOENhYfcHTjCqMwWCrsFH4FSlgqvmsOUM8owBWX+DXPEFOhcEOcgOIvL0UVPNcc4aQRgGsviCy1RS8DIOtoLGlupVEVLN3CEDQ8glg9QWpWlK+fDDY8tlWnpzXcCgHi7uTiJkzhD1WXxBnc8WuwmArZmqJbpQjUT4eOwQgaPkEsPqCZM0gT0YYbHnsGgq58l9zxok6Vl9QcyNjsNXcOvKWTdCaM0+2sfqCvM0TWO4Y7MDsF8pXC1pz5gk2Vl9Qc+NjsNXcOjKWLZCZMwQ5Vl+QsYUCyxqDHZj95L76ulw3ELHmDPGMAlh9Qa7mCThfDHbAJpQvA+neV3uWMcCZM8Q2Vl/wtK0aYjDYamgFrjLISbXoNWeIZxTA6gtcjRf8OAx28NuAowQyUy16zRniGQWw+gJH86kgCoOtgkZwK4L8VEsyc4bYxuoLbg2ohkMMthpagVUG+anms0MAgpZPAKsvsNpPLUEMtlpagipHomTrwH3XSqqZM4Q9Vl/wbXDlz2Kwlbd58O8Y4JozxDMKYPWF4Deqawkw2K72iIyjANecIZ5RAKsvqK3jYLDV1iKyl0famTPENlZfkL3lhNwAgy3EWmGRVpI1Z4hnFMDqC6rqHRhsVTWHEoWRfOYMsY3VF5RoP373wGDzs5McqdYDFMiRr588JZ85Q2Bj9QU/plfwNAZbQWOzb6XI+2r2DVFY8pkzBDZBAFZfQHYObgCDHQz7B49qmWbOENtYfSEY/YnjnhhsDqPIGxU8qiVfc4Z4RgGsviBv5+GdOwabt6kkSRhUqsXtEICg5RnA6guS9JQAM8FgB2hAIZcHm2oJv9b0ATlWXxDSJ+RKi8GWy7Lu+ZYC7HGPU/5Y1pkzRDtWX1C+Zd3uiMF2M0g4H8o9c4bAxuoLQe9GGOygN4FyBZBpzRniGQWw+oJyjerlThhsL4YJx2j51pwhpFEAqy8EtwdhsINrf0XvLt+aM8QzCmD1BUWb1uNmGGwPk0gVQUqVkWT5KDNzhtjG6guStZzwjDDYwm3G54rVAIf4pFMujWIzZwhsrL6gXOt63AmD7WGSwCNU8L7asxKKzZwhsLH6gmcrKBaDwZba1KqkWpk1ZwhpFMDqC1J3L775YbD5WopXOrVSrcyaM8QzCmD1BV7dRoZEGGzpjKpiqiXcIQBByzOA1Rek62ECcsJgCzCWr6RrFFIO9lUG7+eUnzlD2GP1Be/NIuMZDLZExs2RKB95slF+5gyBjdUX5GlSP7lisP0YKDxOK7nmjI00E8bqC8r3Igy28jYPwh2VXHPmCTZWX1C+yTHYyts8CHdUeM2ZJ9tYfUHhVo90sDWuv1atWincAArcLogzZ4hwrL6gQEOzbxHpYCNb5OTkvPLKK/fv30cxvgLXfZ1U27ngzpwhtrH6gpIdA4NdZu3o6Oh169bxMr2631d7ViG4M2cIbKy+4Nk08sVgsCnbrl27Njo6mpeVQ43qYK05QzyjAFZf4NXBJEqEwQaCIF5++eWcHB5vokOQ6iCuOUNIowBWX5AIW//ZYLChWbNmO3bs4DTVrl27qlWrlpSURJ0NTarVMHOGwMbqC5zdTI7ISAd76dKl3bp147RsUlJStWrVHnjggbp16+oX6mEjZyq1R6pk5gyxjdUXlOkxEQ32nTt3Xn31VaPR6GnrpKSkmjVr1qpVa82aNZUfq1zvn/X0er1nMvXHqGTmDIGN1ReU6TMRDXbz5s1dX2NTRwCwa9euRx555Omnn755OCX1v3Bk4/HHHnuscuXKZT65Mi0j0V2Cu+YM8YwCWH1Boob1k01Eg+3NNvPnz3/wwQfr1q1L7NZnV4Dfn0yqUrnaww8/fOiQyuSOvFWAFR/0NWcIaRTA6gus9pEriMHmtuzRo0crV65cr169ba+feurBmjUeqvXz50l6gjuxamNVNXOGwMbqCwp0GAy2VyMfP0554A8/+PCTDz2d8HVK1luO3191bP2FtFq9XqK2E2qbOUNsY/UFubsKBtuXhefNm1ehQoV1dQ/s7EfCKShp5bjyRumkVo5z53xdpZ5zaps5Q2Bj9QW5OwkG28PC6wEKnZFWq9XWl9zxqiM7G+A+wDeQ91Hp0s9ssRMdhOo9c7XNnCGwsfqCs4fJE8Jgu9qVcxXKJsh43f7bDHoHACvAAihtbr/SxtyzrW3VatJicc1BTUcqnDlDbGP1BVl7CgabZV5OqgFAC5YvHDM+sBsM5YmPgKOdo6C9eckIU/ee9tOny+PV9H91zpwhsLH6gqydBYNdbl5vVDPnR0DiJ9bfVrK27bkL5EDS1tKWFFfQ72vzd+Mc9+6VZ6WO/6t25gyxjdUX5OspGGzatr6pBoDfobiJrV+r0uJiVluYAWaBvYW9cHzRhvX5HWJsy1eQJSWsBEENqnbmDIGN1Rfk6yAYbH5fd+SB40vH9q4lGzayBm2mWQ6AI9ph7m5Oj8/5cXZh1+72Y8fkay8BOat55gyxjdUXBLSokKQRD3YpwB5+BhsLOV1LOsaUms0e6dOA7Etav7Tmb80/nZQ9YIh51BhHRoZHMmUj1DxzhsDG6gsydYqIB5u/XQ+ArYVt9remnTu5rjEBTIPSFqWF3xcS+dr1e/I6drEtWUK6uO5c18kUp/KZMwQ2Vl+QqQNgsHkbthAcrR2p0wq6drfbbF6u2k2lKfmqJPtm9q087bQFBZ27lh4+DKSH/+7lesmi1T9zhtjG6guStTorIww2yxh+gz9ASc+S0bHFBw54T3oLyF6ktbU1b2ceYSPik/VfjygZ/q3j9m3vl8hwRv0zZwhsrL4gQ/sDBluIVY9Rznbi73lf9bHb7d4vLAKYTLvlUwq1BVrCRmw+mNuxq3XBQrKQtabN+/USnAmJmTPENlZfkKDJXbOIPLAD8YrN4GjrMP5sHDrG5GfqmwTYBo5WjpK+JfrbesJGpBm1M5cUdIwp3bdPCc88JGbOENhYfcGVSgmOIgzs1QCHA7PadDDHmP84l9N/kN3/k3MSkD1Iaxtr3j7KLSdsxPlU/dDRJYOH2m/eDKwYPq8OlZkzBDZWX/DZnmJORhLYfleh8DHgGcrHzknIGTjUfOYMjwuMABOpSwpmFmiLKLecsBHbj+TG9LDOmUtyiTLxyNNfkhCaOUNsY/UFf60q7HzEgC0J1QBgA7IjWTC7YPepnCHDfTxns5qBpLbOdrR0mAaY9OmUW07YiIxC7dxlxo4xpbt2ga/HdVY2/IMhNHOGwMbqC/zbl0/KyABbKqoZi84DS3sLUUz0GmC+dImPkek0V4DsSlraWnIP5zJsEzbi4h39iHGmAV/br0u6Z1BozZwhtrH6Au/O5D9hBIAtLdUAcIn2xk/lbD2cO2asw7+NUYp8gLHUKhfjPKO2uMwtJ2zErhO5Xb+yxs1w5OWhpAEFQmvmDIGN1RcCanXXi8Md7DWUGyzxz0GNvYVTCjPNRLdeFmHTYA5qabo9ym4abNLd1aGh+06R9udVxg6dS7duJQP0zENu5gyBjdUXJOyo4Q42j317xFhzCViiLdpCaulo7CQhgzZzs0QgO5OW9pbcE063nLARl+/pRsUW9x1gv3xZTKGYa0Jx5gyxjdUXxDe865XhDrZrbSU7ukF9rZl7OPeuiYjpYU1LE55xDsBI2i1fbCTM1HQa+rcvPqdbb8tPU2kxJuEZh+LMGQIbqy8Ib3DuKzDY3HbxE0tS60YLYwsJG/Hbtvyp04UP2gBgB1hO/YEoHlasy3K65YSNuGsilqwzdOhcumEjWVrqpyxup0N05gyxjdUX3BpU3CEGW5zdAFaCtZVVm6fNKNR2iLFlZYnN5wz1/szSyZITn4MGbSZwNUs3dnJRrz72hAQBmYfozBkCG6svCGhs70kx2N5t4/tMGjXY5u2hlpQtWWeYOy+Apao6gGFgi7IZlhnc3HLCRhxOyOnZ1/L9Dw6t1neBqLMhPXOG2MbqC/5b2l+K8AJb0rfB/kxHaZ4VjykmbESqQduuk43SJxb9swEspt3ykcU6rYtbTtiITDOxfLOhfWfb2nV+tisI6ZkzBDZWXxDdj9CFYQS25O+rkZG8BTaAraVNp6M4nLfcuHhxAIM2c4uT4GjvMMeYcxLc3XLCRiRpdbHTi3r0ssfHeysQhPTMGQLbr/pCVJS7BTxj3FNE2HG4gK081UDtH2BvYc/fnk/YiORsXftOpU59YtHdKAtgMO2WrzYQVudUOXr8Pnopu/dA8/iJDs6n+lCfOUNs+1Zf8MTYM0Z0C4THhWEBdlCoZtp/GBQPo7xxwkbELSpw0ScW3UGsAPOoPxlFY4t02e5uOeOZr9xOiaL+tpJ0E2AL9ZkzBHZCAtSsCadOwblz4PkRuyfGnjGizR8eF4Y+2EGkGgB2UKOr7h6F37X71KAtmcjZEerbb3NXc/albDRcswPJ2bofZhZ262E/ebKsK4bHzBnD9o4dEBVV9q9dOzjs+rGtJ8aeMeHBp+hahDjYwaUaAHLAEeXIX09544SN+HF2IYc+sejGuQPkAFr8dGM+p1tO2IiT17L7DTaPGeu4exfCY+aMIKhRulUr6N0b/vtfuH0bvv8evvwSUlKcdkTMswPO0zgEIS2NlCjDOnARfWIMmAaYGLAv3tFz6xOLyJa5xAwwk1ZZmlCozXN+N8IeurMsxNpdeR1ibK1bk717A/JmQzcwdy60bw+pqVC7Npw+DRYLdOkCP//sNKLn+OwZ40wdkaEQH7HV0Gb7qJWh+tSyD60nTCni1icOpKj7y/YkyL7O7ZYTNuJWnvbfr9kavmPfvDnk2Z44Eb76Cvr0gUqVoG1bynAjRsCkSU4LemLsGeNMHZEhDHbAzV5AbRJiWGFgRtEzKXpf+sSi75YGZB/aLd9W5vazB20m/Gxt++L1eT36lfQb4DhzJiTxvncPli6FJk2geXP49lu4eBHORYFWC9HRsGqV03aeGHvGOFNHZAiDLUWzT4KSr0oQaaN86xOLvqEJYArtlv9QqDW6u+VJWt3jVciL94iL94gl6/NatbVOmUrevh0yeF+8CMOHUzPhH34Iq1dDt24QEwPr18P3UdAthnLF2TJSnhh7xog2c3hciMGWoh2PULwhP/nktWw/+sSB3HMX5SCU9CrRJ5c5/8wflI378ho2sl7KJJh/8SnaCdMKWrct3bAB7t9XNd4bNkCzZlCtGnz9NSQllZlGq4WJE6FNG2jZEsbFAOdL+0CsGPbXYrClaOIS6hnYuNiIBm3/+sSB3DYFyK/oPQl2lYmfEjZi7I+F3foVI7CZwJ54fa+BJX36Ujt4q20u7cYNiI2FOnXgtdfgl1/AZOKwiN1O4Q1jAQR+4saRV4RFhQ7Y6wGUUtsX0wemgbmLmbCUrRU7nMBPn1jMnehrCgG+p9yEgqkFzJ4EzVqbpy40uIHNHP66KbdVO+vkH8mUFFXgvW8fdOwIVatSDrZfpdfYWIDT1DbG+CfIAiECdtDfV/s16p8UZjmJzjXefPWJ/ebsLQEJsLV8T4JU/bO17TtPZHOCfSmTOHNL+/3Mgi+jS1evptzaoIze6ekwcyY1Pj//PMyYQX2Ixuc3fTo9mI/mkxancVogFMBWP9UAYAVHB0fB3ALkjQvQJ3Y2h/DQdSC7k4UtrC0rUTNn3sBm4vef0/cdbPqqt/34cUXZPnmSendVvTr1wLx/v7CNUDZtoh+85wGI/uJduFHD4ArVgx0SVDMdYQ5YOlmIkjJv/L5VoD6x6N5khLQYOFWdzJpUcDlN65vtS5nEiu25bTpYJ05y3LwpL97Mu6sPP6TmuseNg3v3xNQwM5N63QU51EId/ONvAXWDHUJUA8AF2hv/0+mNC9Yn5t9urimnToHln4GpqSOnh+n6eb1fts+laifPMX7ZpnTFCsjMlB5v9rurTZvA667DrrXwc4Tnz/wYyOW0isEOLappDTOyC1kwzemNi9EndmkdvgfM15o5f4CpLVnQwnJ7S65fti9lEocS9QOGm7p2tx85IhnbnO+u+FYDp5POAmoFuxRgj3S1VCynRWBpS8kSoydtkfrEAguMvtbU3YCir6Hoc1vmFOPlDD+P3Az8q3fltO1kGTfecf26eLz5vLsSWCecPCALqBXsgCoVvIuvU99R5x51qoWL1yfmXQn3rzWzwDAPTE3s2b2Lr1/U8Rm6z6drpy40tGxT+uuv5L17wvAW9O6Kd51wwkAtgMEO1IIu15NA9iQLJ1GyxOifeH1il6y9HnB+rZmzH0ytSWOU5dZOXm75pUzij0u6waOKY7rZDx70z7a4d1de64BPSG0BDLbUFl0B1tZWbb7TGw9Un9hfAb3pnOmuQVF/yi2/F2e8fIeXW34pk1i/L6d9F8uoMY6rV7nxDuTdlb+q4POSWQCDLZkpyzK6TXnjaKd7ZtwOVJ/YZxl96ZxlgnEmmD63Z/ctvnaZl1t+KZNIzCBmLDa0bG37eRF5924Z3pK8u/JZD3xSSguoBuyAFT6ltEpgeZH9yaKxRcgVl0af2HuR0MyZt/VkubvB1JI0tLKk7M3h88jNpDl2RTdsbFGHzvbVq53fXUn27sp7dTzP3L0LFy6woveywjjoxQLqAHs1gKuolZfShkj0erC2tOr0LjqE0ugTexjAfeaM4PafdZehuA8UNbHdnWO4dJevW75oXd4771sefRQavk0eP+5xb6UidDpYtIh1s58ACliHOMhlARWAHXLvq7ns6BKXScsS73BRRBCnT3z8OCXod+KES/bsA86ZM+6h+y4Yp1JuuX5Q8dVrvtzy49d0wycW1H6+9NUGtrhFxlt52t+2UtsVrFpNWizsmysXZsunQBrAL8rdOkTvFGyww49qpiMMgeIRZbLEyCcXoU88ZQow/7x1L28zZ9xsE5C7HUwtHIY25uSDHG752j05X3YoqVLVEd25ZPcp5xI6wkbc1Ot+mFnUvSf1BajyP+obL/ZvFPsAhzksEFSww5VqANhGyxJnunjjQvWJLRbo1Any8qiPHL0Nlb5mzry45foLUNwTipra7iw0XKK/Gzl7WzsxzljvNVvtf9knTCtI8thjCP1tOnY5u+/X5u/GOcQt/ObogPyi3MHeAHCR35WRmip4YIcx1QCQTcsSb3TxxoXqE58+TSnv/vWLjaXEOjl/fmfOOIdu7R0o+AGKP7cndzX16WZ6orqjSQvzut1597n2HkFUM4EsC7F6JyWKunwFWVLCWSjpI93BtgBMkP4u4ZRjkMBeow7lYFlbcjSYBpXJEiM2BOkTx8VRHzkCwL59EBfHUVaeM2eebDPvrobVh90V4Xz90qSDTiUWVFTfgeQc7Y+zC7t2tx87xlEwyaPKvspm5zsJQKk/K+zbhko4SGDnhIp9AijnHlqWON1FmYywETz1ia1WaNfOuRtG+/ZgtboXRsDMWblb7vbdVWkqkP1p8dNNXvck8EH46aTsAUPMo8Y4MjLcyybtcdlX2exMkwBYuqXsMzgMob1hgMob0EjJmxhWlckSIzx46hOfPQvjxztrOHYstT+G20/QzJnX767MAHHUB6eFE73uSYAK7xm4byXW78nr2MW2ZAkp2fZGbvUEuHQJEhI8YhM9YnBEuQWCNGKX3z7M/z8RSno7ZYkRFXz0iWfNArQpFwAcOwazZ7tbi8/MGd/vrvaBo43D3MOcneR1TwJUfs/ArTzttAUFnbuWHj4sTCDFvUr4WCILYLAlMiRnNn9Q3nj2DXdU/OoTl5ZSWkKlLGkBq5Xay4odAwC+Z84Ef3eVWr4nAb0xsCe9fmPik/VfjygZ/q3j9m1Oc+BI5SyAwZbT1iZalvgXpywxYiMQfeLU1NRZs2a1adOzYsWfDh686DY3FtB3VyaAn2i3fDLHngSo8L4Dmw/mduxqXbCQ9Nz+Vk5b47xdLKAI2OUq8C53jpCDKWDuZvbcK1O0PvGyZSuqVq354otDX3/9t7p1x1Wt+o8hQyYxbEv23dXO8j0JUtxn/nwjjc6mGbUzlxR0jCndtw975sHp6PKDHd7vq/222ilqAMy+6O6NEzZChD5xYmJi1aq1Pv00DW0f27Rp7lNP/btfvy0Baga61yOZ3pOgjTVvt+A3YQjv86n6oaNLBg+137zpnj0+ltsCMoMd4VQzssTtHcZ5HN64CH3ili07vPbaUkQ1E2jU6Pjjj78p/XdXaE+C6QVssSfELc/A9iO5MT2sc+aS7M235O7WOH85wcZUM/1rFi1LbHZqqjBIiNAn/uc/637yyW03sJs3t1Ws+Der52vuwHs3CbCF3pOgXwnaJ5gnz+xkGYXaucuMHWNKd+0Cuz3wYnnkoPWIifgI2cDGVKO+lUDLEp9x+aaC6fdC9YlffbXhBx+cdwP7iy/yH3+8Orqb9IFr1J4ElmhL3gHxbjlhIy7e0Y8YZxrwtf36dTFlNJkgO9vLhd8ByPH3wsvdQiJaHrAx1ezGtwPZmSyIc8oSo9FMqD7xN9+MeOmlIW5gN6g//9MPP2HfUPqwAWA89eepYHaBttip+oQqwj+w60Ru16+scTMceXnCiun+VTb76hOhqWnLroLUYRnAToiAdeBCm2EhWNpZOJEQpE9sNBpr1nyuQYP5UVEkg3fDhlurPv7E7l5Vib0/kA7Wi2+hJfSbngRYR33ZYhpo0t8ROVvO8H+nSPvzKmOHzqVbt5KCPHOXr7LdCow393I1iAxgu94AH1EWuErLEh93yhKjIU6oPnF6evo773z0xBP/fLbm20899a8XXnghMfFXm2Hr7fmNbvz0eknWVXkNfgnILqSlnYUtsYzqIihw+Z5uVGxx3wH2y5f5Ftn9Gy/2dXMA8JM2yyAYbJYx5AuSQPYgCye7yBIjDEToE2dlZf0S/bebV5YAHEf/cv8cc3lEddmH7lyAMdSKOuMCI2FynxFEleIZ2Bef06235aepDq/Pz6xG8QW2HmAWK2nEBzHYSnWBZWBtY9UaOR5QxekTXx5WrbR4F6KaCSg0dNsBfgN7lL14SLHOVUyCJ8/sZHdNxJJ1hg6dSzdsJN3WzLq1jS+wAWA0QBhJYrrVXeghBluoxcSmv0XLEnuZWBahT8wJNoO3QkP3eWpS0NLBkuMqosSGln/4apZu7OSiXn3sHF9xlZuc46vs8lPU/w8AHGUfR3QYg61c85N9yaLxLrLEqN+nGrTtOtn4uKOouD7ABjiu0NCtBxhBu+W/GgmPF/WodvwDhxNyeva1fP+Dg9o61+PH8VU2Ow0JsIZ9HNHhgMFeD1AY0RYUUPm1YP3Sqs3h8MYJGyFUn9g32MoN3XaAXylnpHhEsY5w0XjjzzM7ZaaZWL6ZEkVdu450W3Rz9iwlJsP+paamNm3atFKlStWrV+/Tp09RURH7bCSHAwMbv68W1Hfu0t74Tu5lHkL1iVyEdAUAACAASURBVPmArdzQ/Sc4OjgsnSw5ZznW4bC55RlO0upipxf16GWPj3eauKTE8emnTVJTU1HUO++8M2PGjKKiIr1eP3DgwP79+6NTER4QALbdDmlpcPt2uUYPplpE3xkMxSPdZYlRXxekT8wTbOWGbgJgCKXNavjNQFgCnS1nbHL0UnbvgebxEx1ZWUCSZNu2bTUazbPPPptXvrqlYsWKaJS2WCzVq8u5Ak9EcwfvEr5gX74MPXuWSXDFxED8VLwKRVSjbaFlie9zu6yC9IkFga3Q0G0FWEi75aOL3TZCQX+8hAYyzcTK7fkdYqwff9xXo9F06tSpYsWKb7zxBsN2q1atBgwYsGLFiuTkZFHtEbYX8QJbq6WE9YYMgTNnKOmp0T2hVUtq9MY/wRbQgaOlI3+zuywx6u4/zi7csJHXSxuhYCs3dB8DRzuHOcackyiNW55lyar/xhsajaZ+g7G7DxQePHiwYsWKtWrVysjIyM3N7du37xtvvPHggw++8sorFy9itfGyLskL7DVrIDoaDAb6mtVQsga6dIGFCwX3anwBZYGRYBrsLkuMwOavTywObIWG7nsAg8DW0mZYayB4aJWj6nMGlm9ZrtFoatSssWHf7df7jDuafLRZs2YajaZDhw6oR+Xn50+ZMqV+/fooJsIDvMCOi4OBA2lDDRsJD38JvXuP6W8YN5bXwBLh9uWo/i5aljjD63JrnvrEosFWaOi2AMyh3PKi8UXeXgRwYswZOXfZ3EcrPvp0rQYTFh57o8ULGo1mIN0jq1Wrhp6xCwoKKlasyGHwiIziBfbGjdC6NVCvFktL4e23jR9GdWhetOQ/SynFvSNH5PnENnxbI58SHjKscZclRh2apz5xgGArNHQfosVPu5mzr3BoyKAq8wnMWLz5oYcqVnuyukajadbrQ6Z/9O3bd9y4cRkZGfn5+d99913Tpk3L+s2c8O0//GrGC2yDAWJioFcv2LUL9m0sGPD57XatS7U7z8LIkfDGG/DUU5hwftYuTzUeSvpyyBKj/s1HnzhwsBUaujPK9yTYLGZPAsYmmWbiq0HFg76dpdFoPm7y8eRTfRMJaguSoqKi3r17V69e/bHHHouKiiIIoszEawGulFs7Iv/PC2wASE+HYcPKZsUH9Ci5+XwzOHoUUlKof8eOYcKFdZ5DtCzxTa+DmF99YgCQCmwlhu6S8j0JYgu1+dzrc9AfNc7Aqh35Q8dSi/ZWbNkyb4XhYv6ZsUc6FVryvZrd/NeOZ15PRsIJvmAztigsLJ9CmzMH6teHq1fL2MaEC+osRZSDalzKIYSGurVffWIJwVZo6N5D1bqkZ4mn0DqqNWcgOUcb3bnkQvmsxIgJ1EdyG5J//vUCvWWhN8vHAvyFd6T+hIHtYqX27aF9exewGbzxGO5iJi8Hk8HcnUOWGPVsv/rEkoOtxNB9G8jepLWVNX+H1xd+yAIoMHl2wZxlzimJEROooTvTeg855NwmvgKwlvtMJMQGAHZREbzyCrUvO+LZM4C9dG+d6CQtS3zZqzfuV59YDrCVGLqLAX6k6l74E689CU5dz+7Q3ZRR6HTgGbApETW/Dvkob9YP//gAwAaA5GRq5mz7dl9sYy+dsxeZqVUclFaBzevqS9/6xPKBrcTQvYPek6B3id7nngR/7dfdd0jxtj9clGcQ2P4d8mUAtzitH/6RfMF2E9CLiio3zdat8Nxz1Ho0z+GaMwaP4eWWgxlgjjH7+NrRtz6xrGArMXTfBLInaW1jzdvD/VUMYSPW7c77epT7h67jpxSmletV+HHICwEmI3NHVkAA2F4NM2IENG4MN2/yZRuP4Ywpz9GyxOd8rbv0oU+sANiyD90F1Nw1JX4ax7Enwa08bduYkvOp7it5lqzPP856K+7HIS/22m3D+4QUYJeWwgcfwODBwsBG43nEjuGlQHYiC2ZyyBIj/9yHPrEyYMs+dJMAm6j186b+Jn2aC8NT5htnLOZ4VNlzOmftLpdB3v8MeXhDzFU7KcAGAJ0OatWCZctEsh2xY/gCsLTnliVGbHvTJ1YSbNmH7qtAdiMtbS25B8sep+OT9e26lCCXG1mDsBE3dLpD513cHD8OOVe/D/s4AWC7PWa7m+b0aahRw7lqBQ3IIgKRM4ZfphzR3BMuk0PsTkzYCG/6xAqDLfvQnQ8wjnbL5xQQRdqBI4o3e9GHc7MPc+jHIXfvrOF/LABs/8bgXLUiAmx0SdgT7qBGqsKfuGWJUQ/m1CcOCtjyDt0O6s2zo6Xj1pfm7/qZ/poSRxbgE8AOOZtQScEGoJaseFu1gnAVEQhjwn+lZYkLnO9pPTsxpz5xsMCWe+g2/wl/Pg95zay5x3w5Mp5Wwg65nGDzWbUiAmx0SfgRnkx924ieLT37KxPjqU8cXLDlG7p//RVWxAGMosVPfzYSJQLGbeyQI7YFjNh+nrFRlvxXrSBcRQTCiHCyN1lIr3/2RjVhIzz1iYMOthxDd0YGdO0KhYX07ploT4IsbiUpTnN5dchPoA4aEQG+YAszhtBVKyLARpeEAeGraFniXF/euKc+sUrAlnboHjMG9u9n9bVz1BtBak+CP12mwTmRZiK9OuSzAPSsnMM9KA/Yf30pK27VCsJVRCB0Cb9DyxK7vpv17Ltu+sTqAVuqofv4cerTYNJNmEcPMJxSgDTy3pOA2yHXUooukfOTDewAV62IABtdEoKEk4PI4lFeZYkR5Gx9YrWBHeDQXVICPXpQHx9w/EoBltDip+V7Etwp0u4+6Wtqjdshj6StdmUDW6pVKwhXEYEQInwTLUvsbycNtj6xCsEOZOhesQLmzeOA2hl1mt6ToLMlh16Ey3yVjf7kuQW4HfI9ABHzpC0n2AAg4aoVEWCjS9RPuJbavDJ/q/+vlJE+sWrBFjF0Z2ZSurdGo5Ni7tB9gG/oPQlWGr71sgsaIpzDIbcDfMedcfjFygw2AEi+agXhKiKgZsJHQPEQ/9440idWM9hCh+7x42H3bn5wle9J8Mf7Vr97EnA45FMBGBVtfncL3VTygy3fqhURYKNLVEj477Qs8V2XDyHQ+MMOMPrE6geb59B9+jT1AZHDIQSio3D9VdLcxZx90ZdSBYdDngGwSMiNQjatImDLvWoF4SoioB7C82hZ4rVODSA2zOwwo0+cOOTvnhvfM0Ol2v7rY79ui4VSv71+XTBAi74DWx+S2pNgna89CTgc8pOC7xWKFygCtiCtFRFwSnKJGggfC6b+XjcJYbM9KrZ4UZvoUAHbx9C9Zg3MmiUGnE2b4MZFgNn0ngQTirTeVwFwOORibhhi1ygFNgAouWolENSDSPgB2hv3qRbE4H3yWnab+istBbvVNjj7Lo/b0E0QlF59vncRYR8wOffKPgCOaIe5uzn7KrdbzuGQ+8g3XE4pCHZQVq2EFuGF4GjtMCz3743/JdPZ6+1Zf+z/0zdIKjxrM2y9Pb/RjZ9eL8m6+v33lF6euJ9OB2uRCGk6kP1I65fW/C3crxU4HHJxdw2dq5QFO4irVkKF8B+gpGcJn43sNnR5v1/fNJI8rkJ6/RYp988xa2M+69E8odRWKg0sJoBp1OfchZMKtQaOxbmCHPL//e9/e/fuRQXbu3dvs2bN0GFIBJQFWw2rVlRO+DGqd3rzKtmP2ReHVe0/6OaZMxf9UqTCBFbriV7d03eP7sYM3ZKhsodyeag9CTx2WRHkkCcnJ9erV89qtQKA1WqtV69eyO2/rTjY6lm1ok7CzeBo6zD+zKH1xaaaUtUeVnXX4b1Dht9VIbd+i7Rhw41p09IAjrs9dUtA+C0ge1F7EuTtdNFF46VDzrr9sGHD4uLiAGDGjBnDhw9nnQmNYDDAVtuqFbURPp2WJbb4+Q754rCqmfkrew3IuHQp0S9Iqkqg1/8ZE6PPzi6bIGA/dUsDTRGlOly2J4GrgoWLQ17k625Go7FOnTpXr1594YUXjP7XxPnKKijnggS2OletqITwM1SnzEnw86HixWFVswwrtx4+OWZshqq49VuYKVPSN29Ocksm/dC9DRytHCV9SvS3nGt+XBzyCQAWX9D98ssvVapU+fXXX30lUuu54IGt5lUrwSXcBmRHsmC2L1lixhXPMqzMNG/v1uvuzZvn3ThR7eGFC4l9+xI22wnPEko/dN8o35Ngr9Mtd86QXwTY4ItLh8Oh0WgcwtbE+cpQyXPBAzskVq0Ei/B5lCwxYfLljTMjNmHbtn7P6dhJ6Z6cqDCmtPRE//73ExIu+CibxEP3Xx+WMHsSzHDuSeB0yP1t7qXRBBWQAP4SBLvcobJqRWHCL9He+Clf3jgC+65pR0yPe2lpZ33QopJTW7cmTZ7s/8GB59BNkjw+CAMAEmAjvSfBAJM+nXLLnQ75LwBpvujBYPuyjp9zymutBEJpINfyX9PmALIrWTjFlywxApuwbfttW/zU6akqoddbMXJyqDkznS7eWwK3eD5D96RJfjqX8/SV8j0JDlMKDWUOeU4+/ORM4hnCYHvahHdMiK5akZvwJWCJtmhZ28d6vu7KMqwkbNsI27aMwp0dYrKyss64saGqw7i4tHXrbggqkt+hOzaWdzcDgHyAsbT46Tyjtlhb5pCPBZBojYyQosieNtiuOFNBSXYICoS0YF3rYwy/QcsS08OLG9LMIXvEJmzblqw7P3feLUHYKJn46tWE3r0Jq5VjzsxvMXwM3cLABgAHwBraLR9sun8na/KpvomHjsHvsmOm/A3UAXZ4rFoJ5K+DJ+GldrIXWRjL7Y3fNd3d3v3x28SvzIhN2LalGn5v1+k+ejnslxYlE9jtJwYNuh/IIjlvQ/eYMcabN28KxuYCkDGkpb3l+uELY490Kpyb//7778cK/iMh+LZKXqAasMNp1YpUhH+0ovQ9QpudxR6xb+pvtmzb7tGKlZ+s8o9HH6303sdvn09dwuA9b3ni4sXJShLL8147d16Pjb3DM7GPZOyh+8KFC//+d8NHHnmiRo2XK1b82/Dho5kVoHzhyQEYSbnl2xcv+7zrexqN5qGHHtqzZw/fy1WfTk1gh9+qlQAJ7zOVrHqcrNLW1Csm9+BmwpyZUZhR+18vvvTyyObNLVFR0KKFo3792dWfrHH53nLCti05e1f7ToTBcNoHG8qfMhhOd+mik+r5nxm6Nw98sUqVGg0bbmU2sfjii7x//avdZ5+1EIabHWA5jKw7UqPRfNmmWcOGDR955JGwYVtlYIfrqhWxhJOd800xyQUjB9re+Lfjyeqj33izzr9i3LZkebXepOZtGjODdtyiS7+tvKk8vT7uOGdO6qpVEhepbu1nG/6njGrGGi1a2J955u0tW7YIYrtRo0YajabryzETvutyb1NGw4YNH3roofDwyVUGdtivWhFK+GzC9qlBd+4skXxaf3Rrg2eef++9025gN2mir1LliYykHzKSfrhwamZ0ixu6yz8XpsxVw7+Efau7RCdlX10gYWHSz/z4+N+quxkhKgpee+3X7t378gc7Ly+vcuXKDz744O4Ju899dpiYdGfo0KEajeb111/nn4lqU6oP7BDSWhFKqYj0p9LsjQvyF90gkk8Tyadr/v3ZTz9Nd+vTLVrYH3n4kYvTGl6b8fa1GW+P+XLWnC6xKTPfD/q/mzM+7PbB5nWDBklbkl0j3vh7tTpuRoiKgrff3v3JJ1GCSLt//37D1xs+8uAje6L3jBk9RqPR9O7dO0TXkLpVXJVgh5zWighi+V/SI7+4530G7I8/aPzmmxvc+vSHHybWfv4VNMGG9IndWlr5w717Ydw46W9rtVofe+zx//2vwM0OL700/rvvxgu7nxUM/Q0Nn6Q8cI1GM2DAANJ9hyFh+akntVrBjsBVK95Q//m+7ROD7vR5Ivn0phVzqz1R+4sv8lCfbt7c8kytRlPmT0NgEzaC0ScObicrKKD2ALh7V5ZS9Os3uE6dHlFRJLJD48Y3q1atmZqaKux+CwFagvaAtnLlyg0aNAgbqgFArWCHutaKN0pFxJ9NdXxSkD8nmRm0h3/dr2qVWvXqzX733SMNGix+8qmX23TqfN96nw02o09sswnr5NKmXrAAli2TNsuy3A4fPmwymd59t/E//vHRG2+s/u9/D7z8cmyFyo8vXvmLsPsdA4gCWE1dpNfrKQ98qbAM1JxaxWDjVSvor0DfPFOMlgGbSD596Ouv+v2rzlvvfNixe/fVO1ezkUbhUbHFBw4ErePdugXdu4PJJHEB8vLyhgwZcuHCBerLDpJcuXJl4xb/e6LePzr37xa9Ljr6ULSA+90DaEetMKXWoqHf7wCn0UFoB9QNNl61wrC9NMvW2Kg/msCwbf7sQ8PKBYhhwkagPkgCaSNtOaU5J69lf9XHbrejM8oFSBKGD4ejRyW+o06nmzx5ckFBATvfE8SJhtsbJuYkxuvjX9j4wua0zeyzXsNmgEEA3ejV4+xEpTTq7JiQDasebLxqJSUFLtx2fFZgmHaLSD6tTTxIVnlcm5uCwAYA9KjZujUF1e1UMqc0Z+gY07FjQeiYBw/C6NEe21yLLcjt2zB+PLRrRy5YQOo9dq5HYCfmJK5KWfX31X/PNmf7v9UcgC8BrnAl/AnA5U8HV5pQiAsFsPGqlZQUGJxb0lZHJJ82zJhobv45opoZrqPK3/JYLLB5CzlwIJSSpYcTcvoPsis8y1tUBN26QZrPj5z5c3H3LpXb6dOOkhLy/n0YOxYOHXK5mg12Yk5iz+M9/TvkB+lH640u+TgP0gAEPqo7r1VTKBTAxqtWUlJgVWZpY2P2/gucfjgDNmEjsm3ZhUVkhw5AAvnX4cCh5jNnFO1uixfDkiWS3XH6dNi/34EWgd+/D/Pnu2TuBrZ/hzwDIBpgIq2+4JIT68CfrAorqXqDIQI2XrVy5ZajaUHBuCQ3P9xtxLbZYNs22LqNLLRTn4XtPpUzZLhyz9lpadQAW+RT/VMQCl27glbr6wo3sP045CaA/gA9AXxvxL0B4KKvm4bEudABG69a+TbH9tZlc7MmbD8cgY0es6Oi4PffocBOaSHetxK9BpgvXVKiK5Ik9Wh98KCU92rVCkp9qiB4gu3LIZ8O0Arghr8SWgAm+Euj+vMhBXaEr1rZeI+sEV84eQMn2ExPKy2FhATqVZOdtDPJth7OHTOW/UpHri555AiMGCHZnBlTyu7dIS/PWeC/5tsLC52HAMAJNrdDvod+tN7mcrnXA59ugter1HQipMCO8FUrZy9ChW0F05wq2Qy6zKw4ABA2Qm/Tmy1k+/Zlz9iUcJ+Z6NbLIkKMQFAvNZmovya3bgm6yH/iGTNcXIBr12DgQJerOMHmcMhvA7ShdhGghA0j4xdqYEfyqpWZM6HeUksnC1HiIkuMwKY2mrKRW7eR338PFtKCBvb1e/JiJ8k7aC9bBgsWBERMXl7e/v373bJIS4OuXeH8ebBa4fZt6N8fDh92SeINbBeHvAigN0AvAOke/l0KocqDEAQ7YletfP45TN5LbRLyp4ssMfs9docOEBsLWr1DX+oc2O+aiJgeVqleQXl247t3KfxcV454pvIVEx8fP3z4cLfFJ8wFFy7AsGEQHQ29e4OnwIkPsMsc8tTN8CNAawCpvQlf9VHBudAEOwJXrVy4AFWqQH4B2YUsmOa+SQjqSCSQFtLCppoZt3/blj91ulyD9tixwNpzFpWFb2D+/Pm//CLy3bEPsBmHvMeQHtbmVtjNtzBhky5kwY60VSszZ0ILWvpnEVja+pIlRh44O5BRqO0QY8vKkr7fnjwJQ4aAuG1w2Gu/xZXMN9jX469feP/Cml5rxGUe0leFLNiRtmrl889hDd1Br9OyxEcp1XtB/5asM8ydJ/HckdkMPXvCDb8vkLgQ8eF+cyXnjvMB9qX0S7mdcnXddPVX1ee7hpz7JiEZG8pgR86qFcYPZ55iSWqjucJJ3LLEPlBPNWjbdbJl81hJzb8jr1wJc+bwT+5MeePGDdHutzMXL6+7EnMSE7MTiZFEfov8a4nXBKwhZ2fNhBM8o0IjJsTBjpBVK8gPZzrVCrC2tmrztT4w5jw1b7lx8WLJBu2sLEpKwWAIZkf3NmKnLU0zNjXe2nyLgpznGnLOeiwCyOA8ofbI0Ac7ElatID+c6U63KW88b59za1hOjD0jk7N17TuVSoVibCzs3Bnk/s0JdtLJJMP/DJk/ZDJUC/6ok10nA8AU9nHIhEMf7LBftcL2w8v7FdmfLBpb5Imu35i4RQW/rZRg0I6Ph6+/hqB8711uA+r/nmBfun0pt0Nu9lfZF7MuIrA5lqywc/Ed/g5AueX2vosi4GxYgB3eq1bc/HCmcdeDtaVVp9f5JdktwbX71KBdXCygi3gmtVqhVy+4etXzjNIx7mDrE7VDtfkt869evsqmOiCH/ARACG4QEi5gh/GqFTc/nGEnk/LG83fku3HL5/DH2YUbNgY0aK9bB3FxfBmOj48/e/Ys39QC07mBnb443djUmLIjxZPqgBzy0QKLpYLkYQR2WK5a4fLDy7rNECgeUcyHZLc0AeoTa7UQEwO5ubw6byCLT/jcgA32jSM3DF8Y7k29x0k1EylyhnwOQKh9FhJeYIffqhVOP5zp8tvAFmXTZQr2xgPUJ548GbZu9Q9d4ItP/N+D9Yx9OeVyXts8fR/9hfsXfIAtcoZcDzCLT3FUlCa8wA6/VSucfjjTf7LBEeXI3yjGGxetT5yQQH2J4fsbaQCQZPEJH0qYEfuC7oJ2sDa/Vf6Va1d8Uy3eId/LpzgqShN2YIfTqhUffjjThUaDaZDJzdPmeShCn9hmg7594aI/dRG53W82PQzYGfMzjE2NyXuT/VIdkEPOvrHqw+EIdtisWvHhhzMdaw+1w7M+3fkhF0+qCRshQp940yaY4u+l7v79+xndb2V6/gniRI/pPQxfGO7OvMuTaiYZL9lDZeogz13CFOzwWLXiww9neoMRHK0chlUG/jyzUwrSJ87OpubMPAWA5emWfHONvxp/4IMDugG6C1o/j9Zu2HOrrPC9bQikC1Oww2DVil8/nOldE6GkdwkbV/5hQfrE06bBRm+SvcHq56WQ2S/zwAcHLt+87MYtn0ORM+TBqqzA+4Yv2KG+asWvH8609B+UN559I5s/z+yUPPWJL1+GPn0oGRN1/ZZAbpPcHtN78MGYM00YO+RhDXZIr1rx64czkJnAEe0w/mJk48o/zEef2G6nlMbOnVMX1NQmW1GQMieF2eKHk1u/kWHskIc72CG6aoWnH86wNgXM3cyEVdjn2Qz8fPSJt2+H77/noHr+/Pk6nY7jhAJR9wE6AIyCk5knAwFbzBpyn3LIClSd5y0iAOxQXLXC0w9nGvkUlLYozb4o0hv3rU+cl0fNmbmp9iuz+MRrD7YCfAPQBSCH4yMQv6O0ZwJhDvmPAK4SyF7LGdQTEQB2KK5a4emHM13HCo72DuM8kd64b33imTPLhFtQL1Vs8Qm6o3tgAbVbPVB76UoDtjCH/BaAPPt+u1czsOPIADu0Vq0I8sOZ5p8FlCyxWYw3TtgIb/rE169TX3FZLM4upuTiE+dd2aGjtO7/2rIo9lpxz6GYf4ywGfJQ2NwrYsAOoVUrgvxwpocnUN54zhkXWWL+U2ic+sR2OwweDH/+WYZQkN1vphQeu9VLBbawNeRrvWzBW2YqVfwvksAOlVUrgvxwphfZgexMFsS5yxLzZ9tTn3jXLmpjavTbtGkTp+43SiB7wAww0H23egnBFuCQmwFiZa9ugDeIJLBDYtWKCD+c6QILwdLOoi0WLITGwO+mT2w0UnpmmZkB9i5JL59F71bvqu4gIdjCZshjAf7CW8W/CANb/atWRPjhTPe6SssSHxcsS4xG9SXrDLPn2OrVqzd9+vR58+C339TUbQ/Qj9ab3IskLdgCHPIrAOXP+e5lUsdx5IGt8lUrIvxwpieRQPYgCycLliVGYN/Ku//c/3XSaDQPP1yhadPDZvWMSGn0bvWxHFvqSQ62AIf8R3UQ7KUUEQm2aletiPbDmdZdBtY2Vq1RjDeeZcnq0L2DRqNp0nR0jRqvPfroY4fd9r/z0oFkjzYB9KN3qy/guJXkYAtzyDlKpJaoSAVbnatWRPvhTHe6RcsSHxAsS3yv5N4LL72g0Wi+GT3q3aYpbzbc2aBBg4cffnj69OnB76fT6N3qb3IXRA6wBTjk3IVSRWykgq3OVSui/fDyvkT2JYvGC5YlTkhLqFix4sMPPzx59uS3B3Rad+ho586dqdG7SZPyjIP0/930o/UOr3eXCWwBDrnXogX5RASDrbZVKwH64UxHWgvWL63aHMHe+IWMC0/XerpChQoDf+7YulOURqOZMGFCkPtmCr397Y8cj9aoYDKBHQYOeWSDrapVKwH64Uxnv0t74zuFeeM3dDd6D+695dCWVxu8+uBDD2o0mh9++AHBE5xAEb1VfW8AnxLo8oEd6g55xIOtnlUrAfvhZQQOhuKRAmSJd5/c3W9ov5TcFMJGnE05W+HRh9/96O3gwIzuSgJMBmgDcBtFcQdkBTukHfKIB1slq1Yk8cOZzr+FliW+z1eW+Ldtv6E3XoSNmHZ0WFL2eW6MFIvdRj9a89h/Q1awQ9ohx2DTvfX0aahRA44ehZSU4PyTxA9nwNOBo6Ujf7MYWWLCRsxP/I4P2JryX4UKFRo1anT9+nXJqE+ip8H5zcfLDTYvh3w9gEOy2kuVEQa73JJz5kD9+tSGVEFhWyo/nKnNSDANFilLzB9s5lY2m23x4sXvvfdeuR0D+78RoAdAf4ASXvkoALZ/h/wowAFepVUyEQabZe327aF9+yCALaEfztRmFy1LnCFGllgo2ABgMpn+9re/sewoNkgCTKQXmfHekloBsP075CSA+jb3wmCzemGwVq1I6IcztckHx5cOwxoxssRCwS4uLp4xY8YHH3zAsqPY4Eb60fqQgMuVAdu/Qz4LQC+g2AokxWC7Gjk5GZ56CrZvV3TcltYPZyo0MpxdyAAAD+ZJREFUHkr6usgS7z65e/yU8ex5Ms4wf7CZp+xHH3303XffleAZ+wr98dYc1+bwd6QY2H4cci2AwJL7q1mg5zHYHhbcuhWeew4SEhRiW3I/nKnQIVqW+GaZENqPc36MWxTHSbJbJH+wPQwXQEQ+QFeAQQAstRY+2SkGtn+HXGXeOAabq/+MGAGNG8PNm0qwLbkfzlSoCBxtHMalRmbxycFzB90A9nYYBLAdAN8BtAO4x9UWPuOUBNuPQ74H4ITPsip7EoPNZW8lV63I4YczdZoMmc0y+w/tzyw+8UayW3wQwF5NP1of42oIf3EKg+3LIbfTf578FVix8xhsL6bW6aBWLVi2TN5BWyY/nK7T1iFb0xukZ18WJkusNNiJtOToQi+t4C9aYbD9OOSp/oqr4HkMtndjK7BqRSY/HKC4uPjKuSuOdg7jAmGyxDzB9m41IWdyADoDDAEQu3mQ8mD7cciF1F7WtBhsn+aVe9WKfH44U60ZYI4xC5IlVg5sO8BIekMPwmcT+DwZFLB9OeQ+S6vkSQy2P2vLt2pFTj+8rFbnaFnicwJkiZUDezn9aH3an/19ng8K2H4ccp8FVuwkBtufqeVbtSKbH+6sUimQnciCmQJkiRUC+wz9aP2rs6TiQsECW/0OOQabR4+SadWKdH54aan3reIWgKW9AFliJcDWAXQEGAHgvdQ8WoVKEkSwVe6QY7D5dSHJV61I54fPnz9/27ZtXqtxmfLGc0/wlSWWHWwbwDB6zkyKNZhBBFvlDjkG2ysR7iekXbUihR/Oa9sdB5DdyMKf+MoSyw72YtoJl2i37eCC7dUhv+Hed5Q/xmDztrm0q1YC9sMF7Hr5Ky1LXMBLCE1esE/SE2bSbUUQdLC5HfJVANJ9n867g7okxGC7mMPPgVSrVgL2w4XteplMbxJykJc3LiPYWQDt6S8c7X7MzP900MHmdshLACbxr4QsKTHYAs0qyaqVAPxwXu63R53I3mThBF7euFxgWwG+pnerz/UoXAARagCb2yGfIPiDlgDMwHEpBpvDKH6iAl+1EoAfrtPpxOx6uYqWJc71743LBfY8+tH6oh/TCj2tErA5HPKLABuE1kbK9BhsUdYMZNVKwH64mBLfoWWJd/mXJZYF7CP0o/U6MQX3fY1KwOZ2yEf5Lru8ZzHYouwbyKqVAPxwUWUtu4gcRBaP8i9LLD3YdwHaAoz3pfsvul7qAZvDIf8FIE10zQK9EIMt1oKiV60E4IeLLSt93SZalpjwI0ssMdhmgAH0bvWGgMru7WJVge3ukBcA/OSt4LLHY7ADMLGIVSsC/fCioqIAyud6qRbsUfb8rX5kiSUGeyYteHTNtSTSHakKbA6HfKt0VRWYEwZboMHckgtdtcLbD2dmv5OSktxuGNDhCCge4scblxLs/fSj9ZaAiuz7YrWBzeGQ+66AbGcx2IGZVuiqFX5+uIDFJ4KK/zstS3zXlyyxZGAzu9V/L8ujNaq0CsF2d8hRWZUNYLADtjf/VSv8/HBhi08EFT+PliVe60uWWBqwTQB96N3qCwWVT3BiFYLN4ZALrpYEF2CwJTAi8Fy14s8PF7f4RFgFxoKpv69NQqQBe6qv3eqFFdhnanWCrQaHHIPts+PwP8ln1YpPP/z8+fPDhw8Xs/iEfyGB2ozG1sKmT/HqjUsA9i760XqnoGKJTKxasIPukGOwRXYpjst8r1rx54fn5ORw5Cl5VCE4WjsMy71644GCzexWP0XycnNnqFqwg+6QY7C5e4yYWN+rVvz54WLuKO6aH6CkZwlhJdyEh5nDgMAupHer7+Nnt3pxpea8Ss1gB9chx2BzdhixkT5Wrfj0w8XeT9R1xyjpheyr3LLE4sEmAX7gtVu9qEJzX6RysJ0O+QIARRwyZCYMNjKFRAHOVSv+/HCJ7s0vGzM42jqMP3PLEosHeyv9aL2PXxkkSqVysJFDnpuWC/MkqjO/bDDY/OwkKJXnqhVXPzwvL6+khN8G0ILuyz/xdFqW2MLhjYsE+zo9DR7HvwTSpFQ/2E6HXNnNvTDY0vQwl1zKV63cO358/axZU0eM2P366yXLlzNpmMUnhYUyv+F1KZDHwRlaljiBQ5ZYDNgCd6v3KI34iJAAm3HIj/18bN/MfdOnT1+9enV6err4OvO7EoPNz05CU+l0c6tWq1rpybp1Or704ne1q//3n/+oc/bsWRkXnwgqoQ3IjmTBbA5ZYsFgkwAT6N3q7wgqgTSJQwLsxJzEyb9PfvTpqs/+/aOXXhpdt263KlVq/vjjVGlM4CUXDLYXwwQWvWPHjqeq1f3ssztRUcD8e/vt3ZUqVTt8+HBgGUt39TxKlpgwuXvjgsFeTz9aB6laIQH2ifQTT/79H2++tQ51hs8/J2rWfHPFCunE3zz6BQbbwyRSRDz33Evvvfcnakgm8NJLI0eMUPZJy0ddLtHe+Cl3b1wY2Jfpj7fm+riNvKdCAuxB4wY/X6eXW2f4+OPr1as/zbZOfDy0akUNA23awMWApWYw2GzbShM2GAyVK1ePiiLd2rJRo2MNG34szT0Cz8UBZFeycIq7EJoAsPPo3eq/Dqa4V0iA/d/GnzZsuMOtM0RFQfXqte/cKXuAiY+Htm0hPp5q15MnoX17uBbYt64Y7MARcc+hoKCgUqUnPMF+990//vvfT91TB/F4CViiLdpCFyE0vmA7AMbQu9VnBrECwdwJJDEnkee/9z77/D//2eYJdrVqz2ZmlpmvVSs4c8ZpyZMnwcceEM503kMYbO+2CeBMnTr/fvfdo25t+eIL34xuNA4mApyU92NGvgW/QcsSH3aRJeYL9ir60foE31vJlC4kRuzBE7957l+d3TrDhx9erFHjn8gsUVEoKE0Agy2NHd1y2b9//5NP1mnc+CZqzrfeWl+jxj/z8/PBBrAPYBwA6y+02+UKHZJA9iILY128cV5gJ9CSo4sUKqaP26gf7E2pm15d+2qlGtVfe+0X1Bk+/TS9Ro16GzZsRFVjg42SobMiAhhsEUbjdcmKFb898UTN559v+dJLg/75z3dffLHBlStXeF2pZKKVYG1l1eY5vXH/YGfTO28NBeovVLB/agb7nP7coNODnlz55PLk5cnJyQ0avP3MM2+99NKgOnVaVa1ac/78hWzjscFm4j1j2On9hjHYfk0kPkFeXt7vv/++cOHCU6dO2Wwq4MCzKmm0LPEepyyxH7DtAN/Su9VrPfMKQoxqwd6UuunfW/7dZG+TzOKyp2i73X7mzJmFCxfu2LFDr3ffkdDtGZuZIQ/EoBjsQKwnw7V2WqlXwedwciBZPMYphOYH7KW0E05P3spQecFZqhBs9kDNvz7MrDgzf3bmjHOGnH8Obikx2G4GUccheg5XgPANYGtp0+nKZIl9gR1PU71UHSaiS6E2sD0Hav7GQu+xW7Uqe+/F/1rPlBhsT5uoKYZNuFmegt2nvPH87WWyxF7B1tK71X8LIN2WeoHXRz1gixuoA7eAtxww2N4so7J4WZ/Qh0HxsDJvnBtsG8BQes4sW11mUQnYgQzUMhkUgy2LYdEbi6goap0ge+2BLPcLMNMd9CYh9yhvnBvsRbQTnhDgbaS/POhgq22gRibGYCNTSBlgv6tgz4tIeQ8mrysgwYqXHHBEOfLXU944B9gn6LUoq6Qve+A5BhdsFQ7UyKQYbGQKKQNssAGouZBWraTM3yUv9nO46DVtY8A0gJIldgeb2a1+DIDD5Z4qOQgW2KodqFG7YLCRKaQMuIENQH21I/uPTfg5gXfbR8sSp+pdwEa71ecJzE2p5EEBW80DNTI8BhuZQsqAJ8aeMVLezy0vG8ANtyh/hwX0JiErDC5gz6W/yrzs79rgnVcYbPUP1KgpMNjIFFIGPDH2jJHyfpLkNQlKvipxgn2YfrReL0nWcmWiJNghMVAjQ2OwkSmkDLhhLO8ztqCCb/D+bdkRSnqhRY+P9p7ZAndk3K1eUHl9J1YG7BAaqJG5MNjIFFIG2GBLskJQssKxn8PdZtpKYFXDVRqNpuoTVXJ65EB3AKNkt5UpIwXADq2BGtkZg41MIWXA7T02o4wh5Q0Cz8uD8O3bt1d4qEKtGjUqVqhYv0r9nFPKKtyLqpGsYIfiQI2siMFGpojUAE34xL4TK1So0Kh+owVfjVvxwaJKj1b6v//7v5SUFJUbRT6wQ3SgRu2FwUamiNxAenr6Aw88UKlSpYyUjC3tFmV8dfP7Sd9rNJoXX3xR5UaRA+yQHqhRe2GwkSkiOrBgwYLHHnusfv36OVdytm/eXqFChfr16xOZhFpUnLw0juRgh/pAjeyEwUamiPTAkSNHKlWqVLt2bconb9SI2qvEXq7ipMDXo6LMLyHY4TFQIytisJEpcAB27tz5wAMP1KxZ030HIo+ZNpUYSyqww2agRu2CwUamwAHKAkuXLiUIwqstGMLHq0LwDEAC+eEwG6hRw2GwkSlwIPQsEOCIHX4DNWpCDDYyBQ4EbIFipfXSRYMdrgM1akIMNjIFDgRsgRu0XrqCM23iwA7jgRo1IQYbmSKiA+3atTtw4AAywdGjR5s3b44OhQUUnGkTCnbYD9SopTDYyBQRHcjOzv7ggw+Q+Hnjxo1v3boVqEUQ4WsDzcnb9YLAjoSBGhkKg41MEemBzZs3x8XFAcDy5ctHjhwZEubgCXbkDNSo1TDYyBQ4AJ06dRo4cOAzzzzj/h5brbbhA3ZEDdSooTDYyBQ4ANevX9doNGPHjlXIFssDVWL0DXYEDtSo4TDYyBQ4AAMHDpwwYULt2rWVG7HRc7iouXQfYEfmQI06MQYbmSLSA5s3b165ciUAbNq0KQjP2GzC7/BtC06wI3mgRobDYCNTRHQgOzv7s88+czjKRIbff/99CWbFxVnUBlDM90pPsCN8oEaGw2AjU0R0oG3btgcPHkQmCOg9NspF5kBCAoz8PrtJv7PTFmtPZVzGAzXb3hhstjVwWMUW+Gu9Kus5fMMGSqq9S09z016XW7dxtI8xv7byU/Z+1CquiRJFw2ArYWV8D2ksUP4cnjUavmwJCxbA8ayT/9n2n747J/+vdUH/8enS3CUscsFgh0UzRlglDuylhuv80ZAyJKXurLpN9jaZuaCoS5cIs4LP6mKwfZoHn1SlBf74gwJbrwedURd3jlott2ABdO/uUla2UCxbDdolUfgeYLDDt23Dt2Z6PURHw08/gdlMVfL6depw/nyXCkcgzOz6Y7DZ1sDhkLHA/v3UBqbt20OvXtToPXAgFBa6FB6D7WIOfIAtECoWSE2F5cth7lzYswesVvdSY7DdLYKPsQXCwALsZ+wwqI7QKmBXXKjFcPrQsAAesUOjnXApsQUEWQCDLchcODG2QGhYAIMdGu2ES4ktIMgCGGxB5sKJsQWwBULAAnjyLAQaCRcRW0CoBTDYQi2G02MLhIAFMNgh0Ei4iNgCQi3w/1ScbXmqxoKbAAAAAElFTkSuQmCC[/img][/*][/list]
A dinamikus geometria lehetőségei olykor új problémák felvetésére sarkallhatnak bennünket. Például most is: hogyan kellene megadnunk a feladat adatait, ha el szeretnénk kerülni, hogy a négy adott háromszöglap pontjai fedjék egymást?[br] [url=https://www.geogebra.org/m/pX7a97q5#material/ku3acxnb]Erre itt próbáltunk választ találni.[br][/url]A kapott válasz eredménye egyben[b] [url=https://www.geogebra.org/m/swk9zjys]a propeller tétel következménye[/url][/b] is, amely már -talán - nem igényel semmilyen további magyarázatot.
Post sriptum kiegészítést olykor szokás - illik - írni egy munka befejeztével, ha utólag jutott a szerző tudomására az olvasó számára is fontos információ. Ez jelen esetben így történt.[br][br][url=https://kristofhuszar.github.io/]Huszár Kristóf[/url] az [url=https://eotvos.elte.hu/]ELTE Eötvös Kollégium[/url]ának a diákjaként közölt egy írást arról, hogy a komplex számok alkalmazásával milyen egyszerűvé, elegánssá tehető egy-egy makacs elemi geometriai probléma -mint pl. a fenti - megoldása: [url=http://honlap.eotvos.elte.hu/wp-content/uploads/2016/07/huszar_kristof.pdf][b]Az Aszimetrikus Propeller[br][br][/b][/url]Talán azért is készült a [url=https://users.renyi.hu/~p_erdos/1973-28.pdf]fent már említett [/url]cikk is, hogy megmutassa ugyanannak a problémának az elemi és a komplex számokat alkalmazó megoldását is.[br][br]A GeoGebra eszköztárában is ott van a lehetősége annak, hogy egy az egészen más koncepción alapuló bizonyításnak a szépségét, egyszerűségét is megismerjék olvasóink.[br][br][url=https://www.geogebra.org/search/Tarcsay]Tarcsay Tamás[/url] tanár úr mutatott erre egy igen szép, elegáns megoldást a GeoGebra CAS rendszerének a felhasználásával: [url=https://www.geogebra.org/m/v4xprvxy][b] https://www.geogebra.org/m/v4xprvxy [/b][/url][br][br] Végül hadd idézzünk egy mondatot [url=https://hu.wikipedia.org/wiki/Lov%C3%A1sz_L%C3%A1szl%C3%B3_(matematikus)]Lovász Lászlónak[/url] az [url=https://www.math.u-szeged.hu/mathweb/index.php/hu/]egykori munkahelyén[/url] - díszdoktorrá avatása alkalmából elhangzott - előadásából: [br][i][size=150][br]"Egy feladatra nem azért kell több megoldást adni, mert két megoldás meggyőzőbb mint egy, hanem azért, mert minden új megoldás a matematika szépségének más-más aspektusát tárja elénk." [/size][/i]


