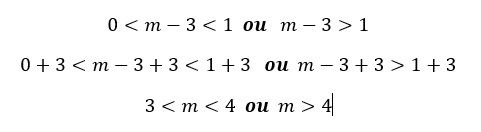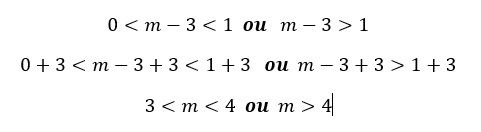
Restrição para os valores da base:
1. Restrição para os valores da base:
Relembrando conceito de função:[br]Função é uma relação onde cada elemento (x) de um conjunto (domínio) obedece uma regra a um único elemento de outro conjunto (contradomínio). Para cada valor do domínio, podemos determinar um único valor do contradomínio.[br][br]Com isso para valores de [math]a<0[/math] não teríamos função bem definida para o conjunto dos números [math]\mathbb{R}[/math] como domínio.[br]Por exemplo: [br][math]f\left(x\right)=\left(-2\right)^x[/math] não representaria uma função [math]f:\mathbb{R}\longrightarrow\mathbb{R}[/math], pois para [math]f\left(-2\right)=\left(-2\right)^{-2}=\sqrt{-2}\notin\mathbb{R}[/math], ou seja, esse valor do domínio não teria imagem.[br][br]Para [math]a=0[/math] ou [math]a=1[/math] a função seria constante [math]f\left(x\right)=1^x=1[/math] e [math]f\left(x\right)=0^x=0[/math], para [math]x\ne0[/math], funções já estudadas anteriormente.[br][br]
1ª Questão:
Para que valores de [b]m[/b] a função [math]f\left(x\right)=\left(m-3\right)^x[/math] é uma função definida em [math]\mathbb{R}[/math]?