Polygons [Grade 7 - Quarter 1]
Polygons
Table of Contents
- Lesson 1: Polygons as composite figures
- Decomposing Polygons into Triangles
- Composing Polygons from Triangles
- Composing Polygons from Triangles - Correct Answers
- Lesson 2: Drawing polygons
- Measuring Angles using Protractor
- Drawing Angles using Protractor
- Drawing Polygons (using ruler and protractor)
- Drawing Polygons (using protractor)
- Drawing Polygons (using protractor) - Answers
- Drawing Polygons (using ruler and protractor) - Answers
- Lesson 3: Categorizing polygons based on properties
- Sort the Polygons
- Categorizing Polygons
- Lesson 4: Angles in polygons
- Angles in Polygons
- Number of Exterior Angles of Convex Polygons
- Lesson 5: Applying properties of polygons in problem-solving
- Exterior Angles - Drill #1
- Exterior Angles - Drill #2
- Exterior Angles - Drill #3
- Exterior Angles - Drill #4
- Lesson 6: Angle pairs in polygons
- Angle Pairs in Polygons
- Lesson 7: Applying angle relationships in problem-solving
- Angle Pairs - Problem Set #1
- Angle Pairs - Problem Set #2
- Angle Pairs - Problem Set #3
- Angle Pairs - Problem Set #4
- Lesson 8: Sum of interior angles of polygons
- Sum of Interior Angles of Polygons
- Lesson 9: Solving problems involving polygons
- Polygons and Angles - Problem Set #1
- Polygons and Angles - Problem Set #2
- Polygons and Angles - Problem Set #3
- Polygons and Angles - Problem Set #4
Decomposing Polygons into Triangles
Description of the GeoGebra applet:
This GeoGebra applet enables you to select the number of sides for the polygon, ranging from three (3) to twelve (12), by adjusting the slider.
Task
For each polygon, use the line segment tool to decompose it into triangles and record the minimum number needed on the table below the applet. Based on these findings, determine the [b][i]pattern for the least number of triangles required to form any polygon.[/i][/b]
Measuring Angles using Protractor
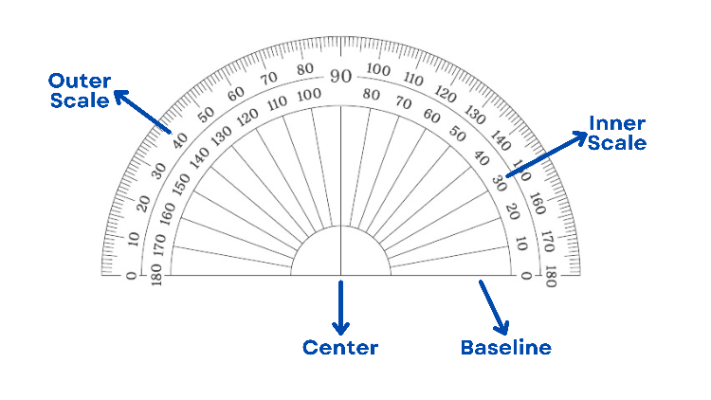
A protractor is a tool used to measure and draw angles. The image below shows the essential parts of a protractor.
Parts of a Protractor
[b][i]Center[/i][/b]: The point at the very center of the semicircle. [br][br][b][i]Baseline[/i][/b]: This is the straight line forming the flat bottom edge of the protractor. It serves as the base for aligning the protractor with the angle being measured.[br][br][b][i]Inner Scale[/i][/b]: This scale also starts at 0° at the same endpoint but increases counter-clockwise until it reaches 180° at the other endpoint.[br][b][i][br]Outer Scale[/i][/b]: This scale starts at 0° at one endpoint of the curved edge and increases clockwise until it reaches 180° at the other endpoint.
How to Measure an Angle using a Protractor
[b][i]Step 1[/i][/b]: Place the [b]center[/b] of the protractor on the [b]vertex[/b] [b]of the angle.[/b] [br][br]In the example below, to measure angle A, place the center of the protractor in point A.
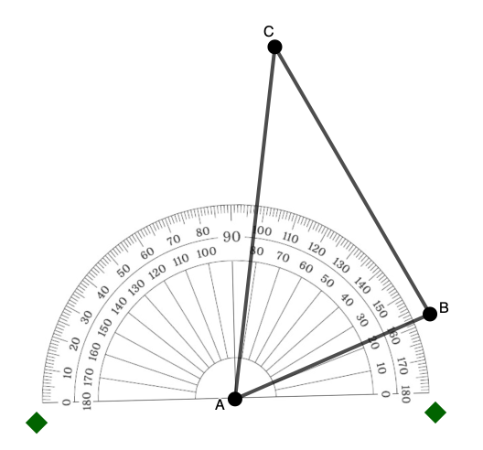
Step 2: Align the [b]baseline[/b] of the protractor with one[b] ray (side) of the angle[/b].[br][br]In the example below, the baseline was aligned with side AB.
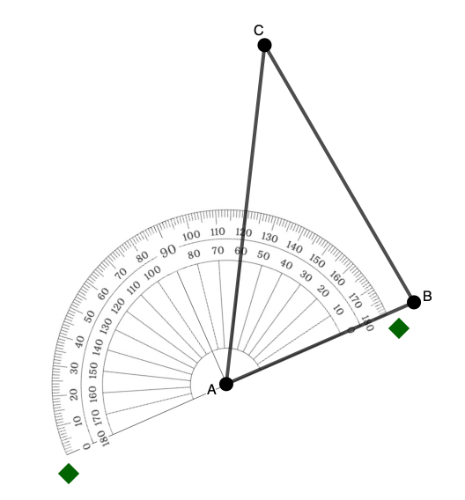
[b][i]Step 3[/i][/b]: Match the [b]0° mark[/b] on the appropriate scale of the protractor with the ray (or side) you aligned in step 2.[br][br]In the example below, the 0° mark where the ray is located is on the inner scale.[br]
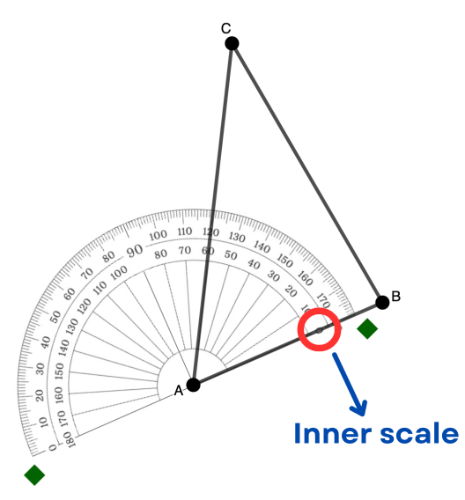
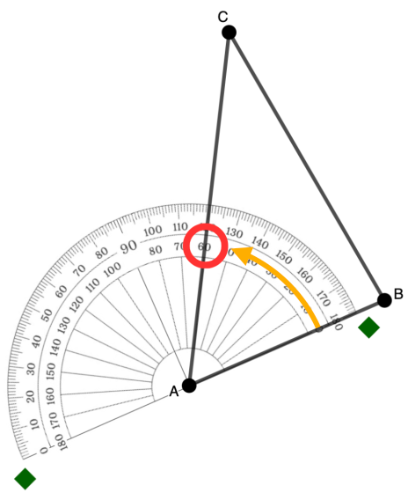
[b][i]Step 4[/i][/b]: Starting from the 0° mark, [b]follow the rotation[/b] from the ray positioned in Steps 2 and 3 up to the other ray (or side) of the angle. The degree marking where the second side of the angle crosses the scale chosen in Step 3 is the angle measurement.[br][br]In the example below, from side AB rotating to the side AC, the side crosses the inner scale at 60°. [br]Thus, angle A has an angle measurement of 60°.
Practice: Measure the angles of the following polygons.
[b]Drag[/b] the [b][color=#38761d]green points [/color][/b]to move or rotate the protractor. [br][br]To display the polygon and the input box for your answers, click the checkbox. If the measurement entered for each angle is correct, a check mark will appear beside the input box.
Sort the Polygons
Sort the given polygons in [b][i]two or more categories[/i][/b]. Write a [b][i]short description in each chosen category[/i][/b]. [br][br][b]Drag the [color=#38761d]green vertex[/color][/b] of each polygon to place them in their category.
Use the GeoGebra applet at the bottim if you have more than three categories.
Describe the category #1 .
Describe the category #2.
Describe the category #3.
Describe the category #4.
Describe the category #5.
Describe the category #6.
Angles in Polygons
In the applet, some sides of Parallelogram ABCD have been extended along straight lines. [b]Explore and identify the patterns[/b] in the [b]relationships between the angles of the polygon[/b].[br][br]Points A, B, and C are draggable to examine different angle sets.
What patterns do you observe between the angles in the polygon?
Exterior Angles - Drill #1
Solve for the exterior angle of each polygon on the figure.
Given the [b][i]measurements of the interior angles of each polygon[/i][/b], solve for the indicated [b][i]exterior angle [/i][/b]on the figure. Type your answer in the input box. A checkmark will appear if the measurement is correct.[br][br]Click the checkbox to solve for each type of polygon. Then, click the "New Polygon" button to generate a new one.[br][br]
Angle Pairs in Polygons
The sides of the following polygons can be extended.[i][b] Click the checkboxes[/b][/i] to show the [b]extended sides [/b]and the [b]angles formed[/b]. Additional angles can also be constructed using the segment [icon]/images/ggb/toolbar/mode_segment.png[/icon]and angle [icon]/images/ggb/toolbar/mode_angle.png[/icon]tools.[br][br][b]Identify pairs of angles[/b] with [b]specific relationships based on their positions or measures[/b].
Angle Pair #1
Determine one angle pair.
Angle Pair #1 - Description
Describe the relation of Angle pair #1 based on their positions or measures.
Angle Pair #2
Determine another angle pair.
Angle Pair #2 - Description
Describe the relation of the angle pair based on their positions or measures.
Angle Pair #3
Determine another angle pair.
Angle Pair #3 - Description
Describe the relation of the angle pair based on their positions or measures.
Angle Pair #4
Determine another angle pair.
Angle Pair #4 - Description
Describe the relation of the angle pair based on their positions or measures.
Angle Pair #5
Determine another angle pair.
Angle Pair #5 - Description
Describe the relation of the angle pair based on their positions or measures.
Angle Pairs - Problem Set #1
Angle pairs in a rectangle and line segments from its extended sides
Solve for the missing angles on the figures. A checkmark will appear if your answer is correct.[br][br]Click the "New Set" button to generate a new problem within that set of questions.
Sum of Interior Angles of Polygons
Description of the GeoGebra applet:
This GeoGebra applet enables you to select the number of sides for the polygon, ranging from three (3) to twelve (12), by adjusting the slider.
Task
For each polygon, use the line segment tool to decompose it into triangles. Then, determine the sum of the interior angles of each polygon using your prior knowledge of the sum of the interior angles of a triangle. Record each sum in the table below the applet.[br][br]Finally, determine the [b][i]formula for the [color=#1155cc]sum of interior angles[/color] of an [color=#1155cc]n-sided polygon.[/color] [/i][/b]
Scratchwork
Using the data from the table above, determine the formula for the sum of interior angles of an n-sided polygon. [br][br]Use the GeoGebra note for solutions and other scratchwork.
Sum of Interior Angles of a Polygon
What is the formula for the sum of interior angles of an n-sided polygon?
Polygons and Angles - Problem Set #1
Click the checkbox to display each set of questions.[br][br]Study the figure and read the given conditions. Solve for the missing angles on the figures. A checkmark will appear if your answer is correct.[br][br]Click the "New Figure" button to generate a new figure within that set of questions.