[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAfMAAAE2CAYAAAB1KntMAAAgAElEQVR4Ae2d349cdf3/e8HVx4tyIcZ4U/4AY2uIQAHbBgRaKrSgbsRIi6EqKkolUYwQ2zsTvSjREDQQukr8EaJUTKlyYcqFUa9swoV3pjHZJpiQtAkJMRr3fPNav+++58z7Obszc2Z2z/s5j5NM9n1eM2f2vB7PmfPY82NmtzVMEIAABCAAAQhUTWBb1WvPykMAAhCAAAQg0Ews8927dze//OUvF+Z22223NT/72c8Wpt89e/Y0P/3pTxem33379jXLy8sL0+/tt9/evPjiiwvT75133tk8//zzC9Pv3Xff3fz4xz9emH4PHDjQPPfccwvT7z333NOsrKzIP10mlvnS0lKzuroqn8yx+JnPfKb597//7dia7OnIkSPNu+++K+9zLH7uc59r3nnnHcfWZE/Hjh1rrly5Iu9zLD766KPN22+/7dia7Omxxx5r3nrrLXmfY/Hxxx9vLl265Nia7On48ePIXJIZo4jMx4BU8UOQecXhjbHqyHwMSBU/BJnn8NgzzyzkCJlLLDZFZG4TpWwEmUssNkVknqNE5pmFHCFzicWmiMxtopSNIHOJxaaIzHOUyDyzkCNkLrHYFJG5TZSyEWQusdgUkXmOEplnFnKEzCUWmyIyt4lSNoLMJRabIjLPUSLzzEKOkLnEYlNE5jZRykaQucRiU0TmOUpknlnIETKXWGyKyNwmStkIMpdYbIrIPEeJzDMLOULmEotNEZnbRCkbQeYSi00RmecokXlmIUfIXGKxKSJzmyhlI8hcYrEpIvMcJTLPLOQImUssNkVkbhOlbASZSyw2RWSeo0TmmYUcIXOJxaaIzG2ilI0gc4nFpojMc5TIPLOQI2QusdgUkblNlLIRZC6x2BSReY4SmWcWcoTMJRabIjK3iVI2gswlFpsiMs9RIvPMQo6QucRiU0TmNlHKRpC5xGJTROY5SmSeWcgRMpdYbIrI3CZK2Qgyl1hsisg8R4nMMws5QuYSi00RmdtEKRtB5hKLTRGZ5yiReWYhR8hcYrEpInObKGUjyFxisSki8xwlMs8s5AiZSyw2RWRuE6VsBJlLLDZFZJ6jROaZhRwhc4nFpojMbaKUjSBzicWmiMxzlMg8s5AjZC6x2BSRuU2UshFkLrHYFJF5jhKZZxZyhMwlFpsiMreJUjaCzCUWmyIyz1Ei88xCjpC5xGJTROY2UcpGkLnEYlNE5jlKZJ5ZyBEyl1hsisjcJkrZCDKXWGyKyDxHicwzCzlC5hKLTRGZ20QpG0HmEotNEZnnKJF5ZiFHyFxisSkic5soZSPIXGKxKSLzHCUyzyzkCJlLLDZFZG4TpWwEmUssNkVknqNE5pmFHCFzicWmiMxtopSNIHOJxaaIzHOUyDyzkCNkLrHYFJG5TZSyEWQusdgUkXmOEplnFnKEzCUWmyIyt4lSNoLMJRabIjLPUSLzzEKOkLnEYlNE5jZRykaQucRiU0TmOUpknlnIETKXWGyKyNwmStkIMpdYbIrIPEeJzDMLOULmEotNEZnbRCkbQeYSi00RmecokXlmIUfIXGKxKSJzmyhlI8hcYrEpIvMcJTLPLOQImUssNkVkbhOlbASZSyw2RWSeo0TmmYUcIXOJxaaIzG2ilI0gc4nFpojMc5TIPLOQI2QusdgUkblNlLIRZC6x2BSReY4SmWcWcoTMJRabIjK3iVI2gswlFpsiMs9RIvPMQo6QucTSKl68eLF54403msuXL7fqNcwg8xpSmn4dJ5H5+fPn117H8Vq+cOHC9L90C5d87LHHmrfeemsL12BzfzUyz7yReWYhR8hcYmkVd+7c2Wzbtq2JjWFtEzKvLbHJ1ndcmYe84zU8fNu3b19VYkfmk70+anv08ePHm5WVFbnayFxiyUVknlmo0enTp5vt27evbQRjXNuEzGtLbLL1HVfm8doNkZ86dWrtj9L4w/TEiRNrr+1rr722GqEj88leH7U9Gpl3SAyZrw9vx44dzdGjR9c2hLHxq21C5rUlNtn6jivzOFwbMh+e0h577KHXMCHzGlKafh2R+fTsGmQ+Gl7IOzaAcc48SX30o/t5DzLvZy6zWqtxZR6nivbu3St/bfpjNV7nfZ+Qed8T6rZ+yLwDP2Su4cXFbnH4MTZ0McWGcNTGUD9DP6rIvB85zGstxpV5/FEae+dqSn+01nBNCDJXCfrUkHmHLJG5hpfOJ6Yr2A8dOtRcf/31+sE9riLzHoczg1UbR+Yh6ZD5qGs+0vl0ZD6DQGb8FFzNnoGWJ4nyfXK0tLTUrK6uyvsci8i8TDUON8bGb/Acedp7KR/d7woy73c+XdduHJnHRW/pdJH6fem1XcPH1dgzVwn61Ngz75AlMi/hpXOI8cI6efLk2i0uEFpvg1g+Sz8qyLwfOcxrLcaReRxVik9kjJri/nht1zAh8xpSmn4dkfn07LgAbohduro3Nm7qVsOhyMGWkPkgDb/xODKPizdHXe8Rp5HidR5Cr2FC5jWkNP06IvPp2SHzIXax0YuNXzpXnu7e6LxjelzffiLzviUy2/XZSOZJ1oOnjAbXIO2V1/JHKjIfTM9vjMw7ZMph9gxvI2HHHsyojWJ+ln6NkHm/8pj12mwk8/SaVrJOnz0fdZX7rNd1Fs+HzGdBsb/Pgcw7ZIPMM7zYI4/bqClknj6qNuoxfasj874lMtv12Ujm6eK2dKQppL68vNzs2rVr7fB6ba9nZD7b10/fng2Zd0gEmf8PXvp4zqiP78SjavysOTLv8OaoYNGNZB6vWXXtRxxeP3PmTAUdtlcRmbd5uM0h8w6JIvP/wYsL39ShyEG08ZgaPr4zuM7IfJCG33gjmafXdby2061mCsi85vQ2XndkvjGjkY9A5iPRWNyBzC1iHNnERjIfuWCldyDzSoMbc7WR+Zig1MOQuaLiU0PmPlmqTpC5ouJT4xvgcpYTfxMC3wCX4bmN/vGPfzS333578+abb7q1NrIfZD4STfV3XLp0qbnnnnuaP/3pT9X3Mm4D7JmPS6rOx7Fn3iG3Rdkz/9rXvta6EOjIkSMdqNWzKDKvJ6tJ1vTJJ59svZ4/9alPTbJ4tY9F5tVGN9aKI/OxMOkHLYLMX3jhhdaGL13d+8gjj1y9KChdHOT288CBA825c+fs+0y5HTx4sDl79qx1v+njZul1nH5+85vf1G9yoyoyNwpTtDJTmd9yyy3NK6+8sjC3PXv2NC+//LJ1vx/5yEekzNNGkJ/6q2vhUheX97///dbv49guxx+n8fHRRdlGf/zjH29iZ2SR+l1ZWRGab5qJz5nv3r27+fnPf74wt1tvvbV56aWXrPv98Ic/jMxHfNc8wq5L2Ovl9b73vc/6fRzb5bvuuqt57rnn7PtMDtq/f3/z7LPPLky/8cfazGTOBXDyj6Kqi/HmVxvBhx9+2PpwbBx65jB7/nx1OhRf+8+nnnpKvp6//vWvV/0+HWflOcw+DqV6HzPTw+zIvN4Xwnpr/oUvfKG1AYycF2HiAjjPlNP3qqc/UuNw7H/+8x/PZge6QuYDMAyHyLxDqItwAVzCc+ONN64J/YYbbkgl+5/I3Dfim266ae31vHPnTt8mhzpD5kNAzGaReYdAF0nm+/btW9v4xUV/izIhc9+k0+s5rntZlAmZeyeNzDvki8w7wKtgUWReQUhTriIynxJcRYvxDXA5rImvZueceYbnNkobP/bM3ZLN/Rw7dqy5cuVKLhiP0uuZPXPfkJF5zhaZZxZyxJ65xGJTZM/cJsqiEWReILErIPMcKTLPLOQImUssNkVkbhNl0QgyL5DYFZB5jhSZZxZyhMwlFpsiMreJsmgEmRdI7ArIPEeKzDMLOULmEotNEZnbRFk0gswLJHYFZJ4jReaZhRwhc4nFpojMbaIsGkHmBRK7AjLPkSLzzEKOkLnEYlNE5jZRFo0g8wKJXQGZ50iReWYhR8hcYrEpInObKItGkHmBxK6AzHOkyDyzkCNkLrHYFJG5TZRFI8i8QGJXQOY5UmSeWcgRMpdYbIrI3CbKohFkXiCxKyDzHCkyzyzkCJlLLDZFZG4TZdEIMi+Q2BWQeY4UmWcWcoTMJRabIjK3ibJoBJkXSOwKyDxHiswzCzlC5hKLTRGZ20RZNILMCyR2BWSeI0XmmYUcIXOJxaaIzG2iLBpB5gUSuwIyz5Ei88xCjpC5xGJT3GyZX758uTl58mSTRLNt27bm2muvbQ4fPtxcvHhx7lz5r2lzR7ylv4D/Z76l+Of+y/l/5h0QI/MO8CpYdDNlfv78+TVxh8B37NjR7N27d+0W4yT1M2fOzJUaMp8r3i1/cmS+5RHMdQWQeQe8yLwDvAoW3SyZnz59ek3Y27dvb06dOlWQOXHixFWhz3MPHZkX6K0KyNwqzqIZZF4gGb+AzMdnVeMjN0PmcWg9DqXH3nfsnY+aYk89HhNin9eEzOdFth/Pi8z7kcO81gKZdyCLzDvAq2DRzZD50aNHx5J0HGIPme/atWtu5JD53ND24omReS9imNtKIPMOaJF5B3gVLDpvmcdeeQg6Dq/HeL0pDq/HY+M2rwmZz4tsP54Xmfcjh3mtBTLvQBaZd4BXwaLzlnk6Vx575+NMyHwcSuM9Jn1i4NZbbx1vAYNHIXODENdpAZmvA2eju5D5RoTqvn/eMj906NDannZIfaMp7cWzZ74RqfHuR+bjcar5UXzOPKc38fG8paWlZnV1NT+D+QiZewc8b5mni9rWu/AtEY7HhMh37tyZSjP/yWH2mSPt1ROyZ96rOGa+MuyZd0CKzDvAq2DRecs8fYZ8nI+bxUfWQuaxNz+vCZnPi2w/nheZ9yOHea0FMu9AFpl3gFfBovOWeToHvtHFb4FqkkPy06JF5tOSq2M5ZF5HTtOuJTKfllzTNMi8A7wKFp23zOOQeQh9o8Ps6Ur2ca5674IVmXeh1/9lkXn/M+qyhsi8Az1k3gFeBYvOW+Zpb3ujL4IZ93FdkSLzrgT7vTwy73c+XdcOmXcgiMw7wKtg0XnLPF3UFt8AN+q8efpSmTi/Ps7h+C5YkXkXev1fFpn3P6Mua4jMO9BD5h3gVbDovGUeCNJedwh9eXm5eeONN5oLFy40v/nNb9a+7S0Ow8fh9ajNe0Lm8ya8tc+PzLeW/7x/OzLvQBiZd4BXwaKbIfPAEJ+HTRfDDf+Mj6/Ne488RYHMEwnPn8jcM9fUFTJPJKb4icyngFbRIpsl80ASh9nj42dx/jztrYfkN3NC5ptJe/N/FzLffOab+RuReQfayLwDvAoW3UyZD+KIPfH0GfSNrnQfXK7rGJl3Jdjv5ZF5v/PpunbIvANBZN4BXgWLbpXMA804F8fNGiEynzXRfj0fMu9XHrNeG2TegSgyHw0vZBQXc8Vt1JXao5fuxz1bKfMgkM6lz/Pfng6SRuaDNPQ4jprExYknT55cuz3zzDPVvL6Ruc7UpYrMOySJzDW8tFc5fDFX/HOLzbgqW6/V5NWtlnmII1jGbTMugkPm679G4o+r+NRB+oRBfMogjddfsh/3IvN+5DCvtUDmHcgicw0vfY/4mTNnrsoo/jNYbPxiY7gZYtJrNll1q2U+2dp2fzQy1wzj9Zr+y1pcoDj4+o1xvM5rmJB5DSlNv47IfHp2fJ3rCHZxNXaIe3hKko89zRomZF5DStOtY5LzOP/PPJ3uGOdf1U63NpuzFDLfHM5b9VuQeQfy7JlreHEldnw+eniKjWEclkTmw2T6Mc+eeZlDnBaK12x8E1/tEzKvPcH11x+Zr89n3XuReYknDjvGxk9933j8Y5HN+FrScq2mq7BnPh23GpYad888fZ3u4KH1GvpT64jMFRWfGjLvkCUyL+HFXnfI/OGHH756xW9c+Xv99deviZwL4EpmfamwZ14mEaeL4o9QhwmZO6Q4ugdkPprNhvcg8xJR7JGHzIdvhw8fbl04VC7Zvwp75v3LZFZrNM6eefrXs+oo06zWYzOfB5lvJu3N/13IvANzZF7Ci3PlcSh9cIq99di7ic9L13S4EpkPpug1Hkfm6SgTMq8z+7hw8dKlS3Wu/BRrjcyngJYWQeaJRP4ZhyXVxULx8Z3YW6/pimBknnN1GyFzt0TLfpB5ZrItD8cbLS0tNaurq+M92OBRyLwdYjosGR9BG55q3MtB5sMp+syPI/N0JXtIwWHiMLtDiqN7YM98NJsN70HmbURp7zvEPTylc+lcADdMpj/zXABXZhGnjOKLjmr9SuLBjpD5IA2/MTLvkCkyb8NLX64xWA15x9XscYhdffZ88LF9G7Nn3rdEZrc+4+yZx29Lf6CG0OM72eP1HH+sxrimU0bRCzKf3eunj8+EzDukgszb8ELWw1exx3ycR48985oufovOkHk7X6e5cWUePYfQ4zU8/NpW14b0mREy73M63dcNmXdgiMzb8GKPZfhW02H1djfIfJiH0/wkMk99p73yeI3X9odp9IDMU5KeP5F5h1yReQd4FSzKnnkFIU25itPIfMpf1ZvFkHlvopjLiiDzDliReQd4FSyKzCsIacpVROZTgqtoMT6alsPio2mZhRwtksxvueWWtXOGN954o2ThWETmjqn+r6f4b2lxDvyGG27wbXKoM/bMh4CYzbJn3iHQRZH5E0880br455FHHulArZ5FkXk9WU2ypk8//XTr9fzggw9Osni1j0Xm1UY31ooj87Ew6QctgsxffPHF1oYvXdH7+c9/vrjYbfjit9rnDxw40Jw7d86+z5TTwYMHm7Nnz1r3mz4mmV7H6ee3vvUt/SY3qiJzozBFKzOVeRy6evXVVxfmFh/F+vWvf23d70033SRlnjaC/Cz/qQxM6mPygQ98wPp9HNvl+GPtJz/5iX2fyUH33nvv2ncBpHn3n9HvysqK0HzTTHzOfPfu3c1LL720MLc4j7y8vGzdb/xzFORUn5zIbLLMrrvuOuv3cWyX77zzzubZZ5+17zM56O67725+8IMfLFS/M5M5380u/yiquhhvfiWGI0eOWB+OjUPPHGYvvzcgHZKv9ee3v/1t+Xp2+f719TY2HGZfj0799830MDsyr/8FoTqIC8EGhf7AAw+oh9nVuADOLtK1hr7yla+0Xs/79+9v/vWvf3k2O9AVMh+AYThE5h1CXYQL4BKeN998s7ntttuaP/7xj6lk/xOZ+0b8t7/9rbnjjjua3//+975NDnWGzIeAmM0i8w6BLpLMA1McWn/33Xc7EKtrUWReV16Tru2jjz7avP3225MuVu3jkXm10Y214sh8LEz6Qchcc3GpInOXJHUfyFxzcanyDXA5yYmvZueceYbnOGLP3DHV3NMi/T/z6BqZ5+wdR8g8p4rMMws5Ys9cYrEpsmduE6VsBJlLLDZFZJ6jROaZhRwhc4nFpojMbaKUjSBzicWmiMxzlMg8s5AjZC6x2BSRuU2UshFkLrHYFJF5jhKZZxZyhMwlFpsiMreJUjaCzCUWmyIyz1Ei88xCjpC5xGJTROY2UcpGkLnEYlNE5jlKZJ5ZyBEyl1hsisjcJkrZCDKXWGyKyDxHicwzCzlC5hKLTRGZ20QpG0HmEotNEZnnKJF5ZiFHyFxisSkic5soZSPIXGKxKSLzHCUyzyzkCJlLLDZFZG4TpWwEmUssNkVknqNE5pmFHCFzicWmiMxtopSNIHOJxaaIzHOUyDyzkCNkLrHYFJG5TZSyEWQusdgUkXmOEplnFnKEzCUWmyIyt4lSNoLMJRabIjLPUSLzzEKOkLnEYlNE5jZRykaQucRiU0TmOUpknlnIETKXWGyKyNwmStkIMpdYbIrIPEeJzDMLOULmEotNEZnbRCkbQeYSi00RmecokXlmIUfIXGKxKSJzmyhlI8hcYrEpIvMcJTLPLOQImUssNkVkbhOlbASZSyw2RWSeo0TmmYUcIXOJxaaIzG2ilI0gc4nFpojMc5TIPLOQI2QusdgUkblNlLIRZC6x2BSReY4SmWcWcoTMJRabIjK3iVI2gswlFpsiMs9RIvPMQo6QucRiU0TmNlHKRpC5xGJTROY5SmSeWcgRMpdYbIrI3CZK2Qgyl1hsisg8R4nMMws5QuYSi00RmdtEKRtB5hKLTRGZ5yiReWYhR8hcYrEpInObKGUjyFxisSki8xwlMs8s5AiZSyw2RWRuE6VsBJlLLDZFZJ6jROaZhRwhc4nFpojMbaKUjSBzicWmiMxzlMg8s5AjZC6x2BSRuU2UshFkLrHYFJF5jhKZZxZyhMwlFpsiMreJUjaCzCUWmyIyz1Ei88xCjpC5xGJTROY2UcpGkLnEYlNE5jlKZJ5ZyBEyl1hsisjcJkrZCDKXWGyKyDxHicwzCzlC5hKLTRGZ20QpG0HmEotNEZnnKJF5ZiFHyFxisSkic5soZSPIXGKxKSLzHCUyzyzkCJlLLDZFZG4TpWwEmUssNkVknqNE5pmFHCFziaU5f/58s23bNnk7ceKEXqiHVWTew1BmuErIfIYwe/hU48r84sWLa9uqU6dOyS5imxXbs8uXL8v7+1I8fvx4s7KyIlcHmUssuYjMM4vBUbwp4sV/5syZNbGH3NMt3ji1TMi8lqSmW09kPh23WpYaV+axnYrtVWyj1HTo0KFmx44d6q5e1ZB5hziQuYZ39OjRZvv27frOiqrIvKKwplhVZD4FtIoWGVfm8biQ+agpRB5C7/uEzDskhMw1vHjx7927V99ZURWZVxTWFKuKzKeAVtEi48o8tlU7d+6UnW10CF4utEVFZN4BPDIv4cV5pfgrt6Zz42UX/6sg81FkPOrI3CPHUV2MK/PYXsVj1bTRIXi1zFbVkHkH8si8hJcufnv44YebkydPtm7lo/tdQeb9zqfr2iHzrgT7vfw4Mr9w4cLazse+ffta26q07Yr6eofg+0QAmXdIA5mX8NKVn/EGGL6Vj+53BZn3O5+ua4fMuxLs9/LjyPz06dPFdmp4uzXqEHzfukfmHRJB5iW8OP9Uw5Wf5ZqXFWReMnGqIHOnNMtexpF5XKy73p533BePqWFC5h1SQuYlvLiKvYYrP8s1LyvIvGTiVEHmTmmWvYwj89jrHnWxbjoEH3vvNUzIvENKyLwNr6YrP9trrueQuebiUkXmLknqPsaReex5j7pYNx2CD6nXMCHzDikh8za8mq78bK+5nkPmmotLFZm7JKn72Ejm6WLd2G6pKZZf7xC8WmYra8i8A31k3oZX24u/vfblHDIvmThVkLlTmmUvG8k8fVPlqG+ljMPvow7Bl79t6yvIvEMGyLwNL1748ZesurUfWcccMq8jp2nXEplPS66O5TaSeVzbs943Va53CL6PBJB5h1SQeRte+v714Z+1nHNqd9M0yHyYiNc8MvfKc7ibjWQe26VR26b48qvYjo3aax/+XX2YR+YdUkDmHeBVsCgyryCkDquIzDvAq2DRjWReQQsTrSIynwhX+8HIvM3DbQ6ZuyXa7geZt3m4zSHznOjofyOTH9MaLS0tNaurq62a88wiyfztt99u7rrrrubvf/+7c6St3pB5C4fdDDK3i/RqQ++8807zyU9+svnLX/5yteY+YM+8Q8KLIvMnn3yydVFbbAQXYULm3ikjc898v/vd7zbXXHPN1W3Wgw8+6NnoUFfIfAjIJLOLIPPl5eWrb4rBq9S/+MUvrl0gMnyxm9P8gQMHmnPnztn3mTI7ePBgc/bs2YXp97777mteffXVhen3/vvvb1555RXrfr/3ve/J7dUTTzwxyaa9ysfOVOYf/ehHm9dee21hbvEfdWJj4Nzz7t275ZtjUOyM9cfx4AIXXgP9eA28973vtd5Oh4Pio3YrKyvyD5GJz5nHhj++Am9RbjfffHPzwgsvWPf7oQ99CJmP+Ow8G+p+bKjJgRw2eg285z3vsd5Oh3PjmqaZyZwL4OQfRVUXf/jDH0qZf/azn7U+XBeHnjnMft46Yw6z++Ub/4dcif2RRx6pejs8zsrP9DA7Mh8HeX2Peeihh1pvkHvvvbe+JqZYYy6AmwJaRYtwAVxFYU2wql/96ldb26s4/RufxnGfkHmHhBfhAriE54Ybblh7g+zatSuV7H8ic++Ikblvvl/+8pevCt23y3ZnyLzNY6K5RZJ5XOwXh6/27NkzEaOaH4zMa05v43VH5hszqvURg4fba+1h0vVG5pMSG3g8Mh+AYThE5oahDrSEzAdgmA2ReTvQia9m55x5G6DTHHvmTmnqXo4dO9ZcuXJF32lYReaGof7/lpB5O1tk3uZRzLFnXiCxKrBnbhVn0QwyL5DYFJB5O0pk3uZRzCHzAolVAZlbxVk0g8wLJDYFZN6OEpm3eRRzyLxAYlVA5lZxFs0g8wKJTQGZt6NE5m0exRwyL5BYFZC5VZxFM8i8QGJTQObtKJF5m0cxh8wLJFYFZG4VZ9EMMi+Q2BSQeTtKZN7mUcwh8wKJVQGZW8VZNIPMCyQ2BWTejhKZt3kUc8i8QGJVQOZWcRbNIPMCiU0BmbejROZtHsUcMi+QWBWQuVWcRTPIvEBiU0Dm7SiReZtHMYfMCyRWBWRuFWfRDDIvkNgUkHk7SmTe5lHMIfMCiVUBmVvFWTSDzAskNgVk3o4Smbd5FHPIvEBiVUDmVnEWzSDzAolNAZm3o0TmbR7FHDIvkFgVkLlVnEUzyLxAYlNA5u0okXmbRzGHzAskVgVkbhVn0QwyL5DYFJB5O0pk3uZRzCHzAolVAZlbxVk0g8wLJDYFZN6OEpm3eRRzyLxAYlVA5lZxFs0g8wKJTQGZt6NE5m0exRwyL5BYFZD5fON8/PHHm23btl29XXvttc2+ffua48ePNxcvXpzvL2+aBpnPHfGW/QJk3kaPzNs8ijlkXiCxKiDz+ca5c+fONZHv3bu3SbcdO3as1ULs8xY6Mp9vvlv57Mi8TR+Zt3kUc8i8QGJVQObzjTP2ykPew9PRo0fXhH7o0KHhu2Y6j8xnirNXT4bM23Eg8zaPYg6ZF0isCsh8fnGeP39+Tdgh7uHp8gAs55EAAA2oSURBVOXLa/ddf/31w3fNdB6ZzxRnr54MmbfjQOZtHsUcMi+QWBWQ+fziPHXq1Jqw46eaYq99+/bt6q6Z1ZD5zFD27omQeTsSZN7mUcwh8wKJVQGZzy/OdCg99tCHp7TXHufR5zkh83nS3drnRuZt/si8zaOYQ+YFEqsCMp9fnOlCN/Ub0oVxp0+fVnfPrIbMZ4ayd0+EzNuRIPM2j2IOmRdIrArIfD5xDp4Tf+ONN5p0W15ebuI8eRxiV+fSZ702yHzWRPvzfMi8nQUyb/Mo5pB5gcSqgMznE2c6jD74GfM0jr3yee+Rp66QeSLh9xOZtzNF5m0exRwyL5BYFZD5fOI8ceLE1b3vGMctHXaPvfbNmpD5ZpHe/N+DzNvMkXmbRzGHzAskVgVkPp844/PjsSd+4cKFq79go6vbrz5whgNkPkOYPXsqZN4OBJm3eRRzyLxAYlVA5vOJMz5yFjIfnOLb3qK2a9euwfJcx8h8rni39MmReRt/+93Wvk/OLS0tNaurq/I+xyIyd0w194TMM4tZjZK01cfO0lXsg3vss/q96nmQuaLiUUPm7RyReZtHMYfMCyRWBWQ++zjPnDmztgce/2RleEqH2tV9w4+dxTwynwXFfj4HMm/ngszbPIo5ZF4gsSog89nHmS5+C6kPT2mvPf7JymZMyHwzKG/N70Dmbe7IvM2jmEPmBRKrAjKffZxxeD3OjY/6j2jpfiX7Wa8NMp810f48HzJvZ4HM2zyKOWReILEqIPPZxxmfMVdf4Zp+U0g+7h8l+/S4WfxE5rOg2M/nQObtXJB5m0cxh8wLJFYFZG4VZ9EMMi+Q2BSmlXl8z0F8I2EsH7dnnnmm9RHKPgM6fvx4s7KyIlcRmUssuYjMM4vB0Xrf8LVZFzcNrs+0Y2Q+Lbk6lkPmdeQ0zVpOI/O4niOu14jTQMO3zfh64Wn6HFwGmQ/SmHCMzDWwdFVynPdMh1XTz804fKrXavIqMp+cWU1LIPOa0ppsXSeVefovfvFzcBsVe+rx9cKx/er7hMw7JITMNbx4Q8z7f1Hr3zzbKjKfLc++PRsy71sis1ufSWSePmGxWf8TYHZdtp8Jmbd5TDSHzDWu+J5t9aUg+tH9rSLz/mYzizVD5rOg2M/nGFfmsRceh9TjK4Zrn5B5hwSReQkv/XvL+Gu39gmZ157g+uuPzNfnU/O948o8ruFZ76OSNTFA5h3SQuYlvHTx22Z8Trj87bOtIPPZ8uzbsyHzviUyu/UZV+ZxFDG+RthhQuYdUkTmJbx0/in+Yca+fftat/LR/a4g837n03XtkHlXgv1dflyZx1758Cds4n8DDF/Nvpn/mndaqsh8WnJN0yDzEl6ce4qL3+Kc+eBt+A1TLtm/CjLvXyazXCNkPkua/XqucWSejiIOnxKM8+hRi1vsucethgmZd0gJmZfwQuQOF5NEZ8i8zNepgsyd0mz30kXmg88U27MaPmMe64zMB5ObcIzM28DSlaHDf+m2H1XPHDKvJ6tp1hSZT0OtjmXGkXnaXo2Sdbo/vjejhgmZd0gJmbfhxUVvca6phi9YaK+5nkPmmotLFZm7JFn2MY7MY6k4hD7qavb43HncF+fQa5iQeYeUkHkbXvqYR7ta7xwyrze7cdYcmY9Dqc7HjCvztAMSX+O6vLx89dvfYofk8OHDazKvhQAy75AUMm/DiwveXD7mEZ0h83a+bnPI3C3R3M+4Mo8lQuhpD33wKvY4X17ThbvIPOc/8QiZt5HFX7O1HJJqr7meQ+aai0sVmbskWfYxiczT0rHtim1YuqV6LT+ReYekkHkHeBUsiswrCKnDKiLzDvB6vug0Mu95SxuuHjLfENHoByDz0Wwc7kHmDimO7gGZj2ZT+z3IvJ0g/8+8zaOYWySZ33bbbWsXg+zevbvg4FpA5q7J/q8vZO6b79NPP722vYpz4IsysWfeIelFkflTTz119Y0Rb47HHnusA7V6FkXm9WQ1zZoi82mo9X+Z73//+80111xzdZv10EMP9X+lZ7CGyLwDxEWQ+UsvvXT1TTF4peeXvvSlqxeKpAtG3H4eOHCgOXfunH2fKbeDBw82Z8+eXZh+77vvvubVV19dmH7vv//+5pVXXrHuN0Q+uJ1K42984xsdtvR1LDpTme/Zs6d5/fXXF+Z2++23N6+99pp1v7feeqt8c6Q3CT+3wWcbDHgf9Ps1cN1111lvp8O78cfaysqK/Mtj4pMNcT71+eefX5jbTTfd1PzoRz+y7veDH/wgskJWvAZ4DVT9Gvi///s/6+10ePdjH/vY7GS+tLTUrK6uyr8MHIuLcJj9mWeekW/i6D0dnnX9yWH2/Jlbx4w5zO6X73e+8x25vYrrX9ynmR5mR+aeL5dPf/rTrTfI/v37m//+97+ezQ50xQVwAzAMh1wAZxhq0zRxPc/gaY+bb765+ec//+nZ7EBXyHwAxqTDRdgzT0z+/Oc/N/GmiHMzizIhc++kkblvvn/961+bO+64o/nFL37h2+RQZ8h8CMgks4sk8+By5MiR5t13350EUdWPReZVx7fhyiPzDRFV/YD4XvVLly5V3cMkK4/MJ6E19FhkPgTEbBaZmwU61A4yHwJiNovMc6ATX83OOfMMz3HEnrljqrmnY8eONVeuXMkF8xEy9w4Ymed8kXlmIUfsmUssNkX2zG2ilI0gc4nFpojMc5TIPLOQI2QusdgUkblNlLIRZC6x2BSReY4SmWcWcoTMJRabIjK3iVI2gswlFpsiMs9RIvPMQo6QucRiU0TmNlHKRpC5xGJTROY5SmSeWcgRMpdYbIrI3CZK2Qgyl1hsisg8R4nMMws5QuYSi00RmdtEKRtB5hKLTRGZ5yiReWYhR8hcYrEpInObKGUjyFxisSki8xwlMs8s5AiZSyw2RWRuE6VsBJlLLDZFZJ6jROaZhRwhc4nFpojMbaKUjSBzicWmiMxzlMg8s5AjZC6x2BSRuU2UshFkLrHYFJF5jhKZZxZyhMwlFpsiMreJUjaCzCUWmyIyz1Ei88xCjpC5xGJTROY2UcpGkLnEYlNE5jlKZJ5ZyBEyl1hsisjcJkrZCDKXWGyKyDxHicwzCzlC5hKLTRGZ20QpG0HmEotNEZnnKJF5ZiFHyFxisSkic5soZSPIXGKxKSLzHCUyzyzkCJlLLDZFZG4TpWwEmUssNkVknqNE5pmFHCFzicWmiMxtopSNIHOJxaaIzHOUyDyzkCNkLrHYFJG5TZSyEWQusdgUkXmOEplnFnKEzCUWmyIyt4lSNoLMJRabIjLPUSLzzEKOkLnEYlNE5jZRykaQucRiU0TmOUpknlnIETKXWGyKyNwmStkIMpdYbIrIPEeJzDMLOULmEotNEZnbRCkbQeYSi00RmecokXlmIUfIXGKxKSJzmyhlI8hcYrEpIvMcJTLPLOQImUssNkVkbhOlbASZSyw2RWSeo0TmmYUcIXOJxaaIzG2ilI0gc4nFpojMc5TIPLOQI2QusdgUkblNlLIRZC6x2BSReY4SmWcWcoTMJRabIjK3iVI2gswlFpsiMs9RIvPMQo6QucRiU0TmNlHKRpC5xGJTROY5SmSeWcgRMpdYbIrI3CZK2Qgyl1hsisg8R4nMMws5QuYSi00RmdtEKRtB5hKLTRGZ5yiReWYhR8hcYrEpInObKGUjyFxisSki8xwlMs8s5AiZSyw2RWRuE6VsBJlLLDZFZJ6jROaZhRwhc4nFpojMbaKUjSBzicWmiMxzlMg8s5AjZC6x2BSRuU2UshFkLrHYFJF5jhKZZxZyhMwlFpsiMreJUjaCzCUWmyIyz1Ei88xCjpC5xGJTROY2UcpGkLnEYlNE5jlKZJ5ZyBEyl1hsisjcJkrZCDKXWGyKyDxHicwzCzlC5hKLTRGZ20QpG0HmEotNEZnnKJF5ZiFHyFxisSkic5soZSPIXGKxKSLzHCUyzyzkCJlLLDZFZG4TpWwEmUssNkVknqNE5pmFHCFzicWmiMxtopSNIHOJxaaIzHOUyDyzkCNkLrHYFJG5TZSyEWQusdgUkXmOEplnFnKEzCUWmyIyt4lSNoLMJRabIjLPUSLzzEKOkLnEYlNE5jZRykaQucRiU0TmOUpknlnIETKXWGyKyNwmStkIMpdYbIrIPEeJzDMLOULmEotNEZnbRCkbQeYSi00RmecokXlmIUfIXGKxKSJzmyhlI8hcYrEpIvMcJTLPLOQImUssNkVkbhOlbASZSyw2RWSeo0TmmYUcIXOJxaaIzG2ilI0gc4nFpojMc5TIPLOQI2QusdgUkblNlLIRZC6x2BSReY4SmWcWcoTMJRabIjK3iVI2gswlFpsiMs9RIvPMQo6QucRiU0TmNlHKRpC5xGJTROY5yollvnfv3uYPf/jDwtzuuOOO5vXXX1+Yfu+8887md7/73cL0u3///ubs2bML0+8999zT/Pa3v12Yfu+9997mzJkzC9Pv4cOHm1/96lcL0+8DDzzQvPzyywvT7yc+8YlmZWUlG3xgNLHMB5ZlCAEIQAACEIBADwgg8x6EwCpAAAIQgAAEuhBA5l3osSwEIAABCECgBwSQeQ9CYBUgAAEIQAACXQgg8y70WBYCEIAABCDQAwLIvAchsAoQgAAEIACBLgSQeRd6LAsBCEAAAhDoAQFk3oMQWAUIQAACEIBAFwL/DwEpwAn8W0Z3AAAAAElFTkSuQmCC[/img][br][br]Are these rectangles similar? Explain how you know.

[size=150]Tyler wrote a proof that all rectangles are similar. Make the image Tyler describes in each step in his proof. Which step makes a false assumption? Why is it false?[/size][br][br][list][*]Draw 2 rectangles. Label one [math]ABCD[/math] and the other [math]PQRS[/math].[/*][*]Translate rectangle [math]ABCD[/math] by the directed line segment from [math]A[/math] to [math]P[/math]. [math]A'[/math] and [math]P[/math] now coincide. The points coincide because that’s how we defined our translation.[/*][*]Rotate rectangle [math]A'B'C'D'[/math] by angle [math]D'A'S[/math]. Segment [math]A''D''[/math] now lies on ray [math]PS[/math]. The rays coincide because that’s how we defined our rotation.[/*][*]Dilate rectangle [math]A''B''C''D''[/math] using center [math]A''[/math] and scale factor [math]\frac{PS}{AD}[/math]. Segments [math]A'''D'''[/math] and [math]PS[/math] now coincide. The segments coincide because A'' was the center of the rotation, so [math]A''[/math] and [math]P[/math] don’t move, and since [math]D''[/math] and [math]S[/math] are on the same ray from [math]A''[/math], when we dilate [math]D''[/math] by the right scale factor, it will stay on ray [math]PS[/math] but be the same distance from [math]A''[/math] as [math]S[/math] is, so [math]S[/math] and [math]D'''[/math] will coincide.[/*][*]Because all angles of a rectangle are right angles, segment [math]A'''B'''[/math] now lies on ray [math]PQ[/math]. This is because the rays are on the same side of [math]PS[/math] and make the same angle with it. (If [math]A'''B'''[/math] and [math]PQ[/math] don’t coincide, reflect across [math]PS[/math] so that the rays are on the same side of [math]PS[/math].)[/*][*]Dilate rectangle [math]A'''B'''C'''D'''[/math] using center [math]A'''[/math] and scale factor [math]\frac{PQ}{AB}[/math]. Segments [math]A''''B''''[/math] and [math]PQ[/math] now coincide by the same reasoning as in step 4.[/*][*]Due to the symmetry of a rectangle, if 2 rectangles coincide on 2 sides, they must coincide on all sides.[/*][/list][*][/*]

[size=150]Statements:[br][list=1][*][size=150]All equilateral triangles are similar.[/size][/*][*][size=150]All isosceles triangles are similar.[/size][/*][*][size=150]All right triangles are similar.[/size][/*][*][size=150]All circles are similar.[/size][/*][/list][/size][br]If it is true, write a proof. If it is not, provide a counterexample.

Repeat with another statement.[br]

They are similar. What are the possible dimensions of these golden rectangles? Explain or show your reasoning.

[list=1][*]Draw 2 isosceles triangles [math]ABC[/math] and [math]DEF[/math] where [math]AC=BC[/math] and [math]DF=EF[/math].[/*][*]Dilate triangle [math]ABC[/math] to a new triangle [math]A'B'C'[/math] using center [math]C[/math] and scale factor [math]\frac{DF}{AC}[/math] so that [math]A'C=B'C=DF=EF[/math].[/*][*]Translate by directed line segment [math]CF[/math] to take [math]A'B'C[/math] to a new triangle [math]A''B''F[/math]. Since translation preserves distance, [math]A''F=A'C=DF[/math] and [math]B''F=B'C=EF[/math].[/*][*]Since [math]A''F=DF[/math], we can rotate using center [math]F[/math] to take [math]A''[/math] to [math]D[/math].[/*][*]Since [math]B''F=EF[/math], we can rotate using center [math]F[/math] to take [math]B''[/math] to [math]E[/math].[/*][*]We have now established a sequence of dilations, translations, and rotations that takes [math]A[/math] to [math]D[/math], [math]B[/math] to [math]E[/math], and [math]C[/math] to [math]F[/math], so the triangles are similar.[/*][/list][br]Explain which step is invalid and why.

Which statement provides a valid justification for why all circles are similar?

Which pair of polygons is similar?

[size=150]Select [b]all [/b]sequences of transformations that would show that triangles [math]ABC[/math] and [math]AED[/math] are similar. The length of [math]AC[/math] is [math]6[/math] units.[br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAARUAAAFdCAYAAAAt5fnjAAAgAElEQVR4Ae1dB5QUxdZ+CIhkHggoQRARCRIUQSQnUSSJICCScxJJIkqQpARBogqSRUCCIFmCiMRFkuSgoCBBkpJBYLn/+er9ve7Ozsx293So6r73nDkz013h1lddX1e89z/EwggwAoyAhQj8x8K0OClGgBFgBIhJhR8CRoARsBQBJhVL4eTEGAFGwDSpREdHU/v27alv3766UET4VatW0dSpU6lfv34i3rlz50Tc+/fvi//4dkug371798hNHdwqO+fLCFiJgGlSmTFjBv3nP/+hDh06hNUHjXXRokVUvXp1WrJkCXXs2JE+//xz8V2/fn2aNWsW1a1bl2rUqOFKg75y5QrVqVOHihQpQunTp6du3bq5okdYEPkmI6AQAqZI5cKFC5Q/f35BKvXq1QtZ3N9++41atWolwqFHc/fu3ThhQThPPPGEuD9kyJA495z4c/ToUSpTpgy1bNmSDh8+TMePH6dBgwbRvHnznMie82AEPImAYVLB8KBFixbUvHlzQQYVK1YM+mY/e/YsFS5cWISZMmVKSPDatGkjwmzdujVkGDtugNCge+nSpQm/ISA+9L7Kly9vR5acJiPgCwQMk8quXbuoRIkStHr1atEACxQoEI9U0EgxnEEDxZs/nKBXgEasNexwYa28N2zYMKHf5MmTY5L9/vvvBbGgB8PCCDAC5hAwRCpo+E899ZSYBzl9+rRolJkyZYpHCNOmTRP3cubMSVevXg2rGSZt8XFS0NsCMYL01qxZQ9u2bRNksnnz5nhlcVIvzosR8AIChkhl4cKFVLt2bdHwsFKCRolP7LkSNNgXX3xRXO/evXuCGCE8PuHkxIkThF6Ekc+xY8dCJgly1OZyhg8fTmPGjKGxY8cKnUFwTveaQirKNxgBBRHQTSromWB1ZO/evaKYaHgaqZw/fz6m6JhL0a5v2LAh5nokP5YuXSpWaLBKE+rTtm1biv3BqlIoAQmmSpUqhkS0cJishe6tW7dOkOi0OPzNCDACcRHQRSroSYwYMUIMEdBDQaO8c+cO5c6dWzRCNEZNtm/fLq6lTp1a7PvQrof61tMr0HozRr9D5YkyQD8QyNq1a2OCab2vQoUKxel9xQTgH4wAI5AgArpIZf78+ZQoUSJKkyYNZcuWjfLmzUvFihWjSpUqiYaJuQhNDh48KK6VK1cuwWEEJksnTpyoRXXsG6SYJ08eoedff/0Vk69GKsmTJ2dSiUGFfzACxhBIkFTQk8iVKxft2bNHDAm03gKu16xZUzTMBQsWxOSKhgniSZYsGd24cSPmeuCPU6dOUYoUKQjDpYRk06ZNYjJXm9TV840J2FACHcuWLSt0x7BOk9hDOoRhYQQYAeMIJEgqI0eOpFKlSgXtdTRq1Eg0TAyNNAHp9OzZU1wPtYkMYbD6MnDgQF1zFxhezZkzx9AHJBhOtB3BsXtZ6MFgSISJZiaVcOjxPUYgNAIhSeXvv/+mb775RjQybLMHEWiC3+hhYHUHjbBPnz5iuKCFQYPE9cyZMxMarXYd33/88Qd9/PHHNG7cuJjrWrpOfuPcEfbY4JiBph+GedA7KirKSVU4L0bAUwgEJRW8sdGTwJ4U7ENJkiQJxV7J0Ta+oQHG/gROeuJMD+5j+bZTp05UtWpVSps2rdgXojVkN9HEShY26eXLl4+KFy8uJp6x0qRn8thNvTlvRkBmBIKSChRGbwMfNLBgBKDd08IFC4O46NFgRWjnzp105swZ6RosdDx06BDt3r2brl+/HrSsMlcg68YIyIZASFKRTVHWhxFgBNRAgElFjXpiLRkBZRBgUlGmqlhRRkANBJhU1Kgn1pIRUAYBJhVlqooVZQTUQIBJRY16Yi0ZAWUQYFJRpqpYUbsQgNlTGArTPl26dKHRo0cTNoCyGEeAScU4ZhzDYwhgxzg2aX7wwQfi8/bbb4tNmjAyxsRivLKZVIxjxjE8hgBIJEeOHHFKhc2QIBoQDosxBJhUjOHFoT2IAMx0NG3aNE7J0EMBqcA0KosxBJhUjOHFoT2IAMhj1KhRcUqGoRDOqfHwJw4suv4wqeiCiQN5FQFtmNOsWTPq378/4RuO5eBeBvdYjCPApGIcM47hIQQ0zw/aJG2tWrXE/ApWgFjMIcCkYg43juURBDCXgjmV2IIl5mBDothh+HdoBJhUQmPDd3yAAIY5WP0JlGCTt4Fh+H9wBJhUguPCV32CQLAVHm3lB0MiFuMIMKkYx4xjeASBH374QQxzMNzRBJOz2FnLKz8aIsa/mVSMY8YxPIIAlpHRUwn8YOjDKz/mK5lJxTx2HFNxBNBDQW9F+zCRWFOhTCrW4MipMAKMwP8jwKTCjwIjwAhYigCTiqVwcmIyIQDzBS+//LI417Nx40aZVPO0Lkwqnq5e/xYOTuICJ2C3bt3qX0AcLDmTioNgc1bOIHD16tV4hAKCadeunTMK+DwXJhWfPwBeLD5c6wb2UvC/Xr16XiyudGViUpGuSlghKxAoVapUPGJh2yhWIJtwGkwqCWPEIRRE4MCBA3FIJXv27AqWQk2VmVTUrDfWOgEEJkyYIEhl8eLFVL9+ffH7559/TiAW37YCASYVK1DkNKRDIE+ePFSgQAGh1/fffy9IBeTCYj8CTCr2Y8w5OIzArl27BImMGTMmJufKlSuLa+fOnYu5xj/sQYBJxR5cOVUXEWjUqJEgkFu3bsVoMW/ePHGNLbrFQGLbDyYV26DlhN1CAMvHLVq0iJc9bM/iHou9CDDC9uLLqTuMwNixYwVxREVFxcv5s88+E/eGDRsW7x5fsA4BJhXrsOSUJEAAXgWfffbZoJrcu3ePsLScLl26oPf5ojUIMKlYgyOnIgEC6J1geIPl5FAyaNAgEWbmzJmhgvD1CBFgUokQQI4uDwLYhp84cWKKjo4OqRRWf5InT0758uULGYZvRIYAk0pk+HFsSRDA0Aa9lPbt2yeoEaznI+zatWsTDMsBjCPApGIcM44hIQIjRowQRKHHJKS2hb9SpUoSlkR9lZhU1K9DLgERZcmShUqWLKkbC20vCwiGxVoEmFSsxZNTcwEBWHXDcGb69Om6c9+wYYOIA3JhsRYBJhVr8eTUXECgdu3alDJlSsM5w9QkyOjSpUuG43KE0AgwqYTGhu8ogAC24oMYunbtaljbhQsXirjvvPOO4bgcITQCTCqhseE7CiAwZMgQQQyHDh0ypW2xYsVEfFOROVJQBJhUgsLCF1VBIGPGjFShQgXT6k6aNEmQyieffGI6DY4YFwEmlbh48D+FENDspMyZMycirR9//HECObFYgwCTijU4ciouIFCtWjVKnz59xDlrQ6hIySliRTySAJOKRyrSb8W4cuWKGLb06tUr4qJj9SdNmjRUqFChiNPiBIiYVPgpUBKBAQMGCFI5fvy4Jfr36NFDpLd+/XpL0vNzIkwqfq59hcueNm1aqlq1qmUlOHr0qCCVl156ybI0/ZoQk4pfa17hcq9cuVIQwKJFiywtRbNmzUS6R44csTRdvyXGpOK3GvdAeV988UVx1sfqomzZskWQCsiFxTwCTCrmseOYLiBw8eJF0fD79+9vS+41atQQ6WMimMUcAkwq5nDjWC4h0Lt3b9Hoz5w5Y4sGS5cuFem///77tqTvh0SZVPxQyx4qI6y2vfrqq7aW6IUXXhDEYmsmHk6cScXDleu1oi1ZskQ09hUrVthaNDhyxyHFcePG2ZqPVxNnUvFqzXqwXOXLlydsqXdC4DYVhp9YjCPApGIcM47hAgKYQ0HvAVvqnRDNPOWCBQucyM5TeTCpeKo6vVuYnj17ClLB6o8TcvXqVXGuqGjRok5k56k8mFQ8VZ3eLUySJEmoQYMGjhYQ54rQO9q8ebOj+aqeGZOK6jXoA/0xBEHjXrdunaOlxbki5Fu9enVH81U9MyYV1WvQB/rDSr5bzr9at24tiOXYsWM+QNqaIjKpWIMjp2ITAidOnBCNetSoUTblED7Z7du3i/xBLiz6EGBS0YcTh3IJgS5duohGjYlTtwTW+jEMunHjhlsqKJUvk4pS1eU/ZdGYmzZt6mrBtVPR/fr1c1UPVTJnUlGlpnyo5+zZs0UPQYbVlzJlylDSpEl9WAvGi8ykYhwzjuEQAs899xwVKVLEodzCZzNz5kxBcBMmTAgfkO+yOUl+BuRE4NdffxWN+LPPPpNGwfz589Njjz0mjT6yKsI9FVlrxud6dejQgRIlSkTwQCiLjB49WhDd4sWLZVFJSj2YVKSsFlYKE7Rt27aVCoibN29SpkyZqESJElLpJZsyTCqy1QjrQzNmzBA9gp07d0qHRp8+fYRu27Ztk043WRRiUpGlJliPGAQKFy5Mzz//fMx/mX788ccflDhxYsLeFZbgCDCpBMeFr7qEwMGDB0VPYMqUKS5pkHC27du3Fzr+/vvvCQf2YQgmFR9WusxFxnb4hx56iKKjo6VVc/fu3YJUMJnMEh8BJpX4mPAVFxHABG3nzp1d1EBf1q+//rogltu3b+uL4KNQTCo+qmzZizpp0iTRUPfv3y+7qrRmzRqh66BBg6TX1WkFmVScRpzzC4kAzBuUK1cu5H3ZblSsWJFSpEghm1qu68Ok4noVsAJAYM+ePeLNP2vWLGUA+frrr4XOkydPVkZnJxRlUnECZc4jQQRwEjldunQJhpMtQKFCheiJJ56QTS1X9WFScRV+zhwI3L17V7zxYdxaNRk/frzQfdmyZaqpbpu+TCq2QcsJ60Xg008/FQ3z6NGjeqNIEw6EmDVrVipdurQ0OrmtCJOK2zXA+YvhQ5UqVZRFYsCAAYIUd+zYoWwZrFScScVKNDktwwhoNmBVdtp19uxZSpYsGdWrV89w+b0YgUnFi7WqUJneeOMNypw5s0IaB1f1rbfeEr2VU6dOBQ/go6tMKj6qbNmKClMC2EHbt29f2VQzrA827KEsb7/9tuG4XovApOK1GlWoPJrRI68czGvYsKEglnv37ilUC9aryqRiPaacok4EYJqxZs2aOkPLH2z9+vWCVIYOHSq/sjZqyKRiI7icdGgEtmzZIhqg1/Z3YBUrbdq0oQvugztMKj6oZBmLWLduXcqRI4eMqkWkk+b3efr06RGlo3JkJhWVa09R3S9fvix6KR9++KGiJQivdtGiRSlv3rzhA4W5+8MPP9Bvv/0WJoTct5hU5K4fT2o3fPhwQSpnzpzxZPkmTpwoyvfdd98ZLt+0adNE3A8++MBwXFkiMKnIUhM+0uORRx4hGDnysmBoV6FCBUNFRO8EhyoRl0nFEHQc2M8IaCskMHLkZcHQDvtWfv75Z93FhC0ZkIn2rTuiZAG5pyJZhXhdHSwh58mTx+vFpIsXL1KqVKkIe1f0CMgEXgQgTCp6EOMwjAARXbhwQby9R4wY4Qs8unXrJsr7559/hi2vZkgb3xAmlbBw8U1G4F8EBg8eLBoZyMUPcvjwYVHeHj16hCzu33//LZzQjxo1KiYMk0oMFPyDEQiPQPr06alx48bhA3nsbpMmTQSxhCoWzgqBRGILk0psNPg3IxACgdWrV4vGtXHjxhAhvHl506ZNotzBhnzYj4LJXGyUwwS29ilSpAg1a9ZM/EdPRjXhiVrVakxRfV9++WWCPVc/SrVq1ShDhgzxio7JWZBKuA+IRzVhUlGtxhTU9/Tp06LhwJ6rH2Xx4sWi/F999ZWu4vPwRxdMHMjPCGhv5CtXrvgWBjicL1iwoK7yM6nogokD+RmB1KlTU6tWrfwMAcHhPIY5a9euTRAHTN5iu76qwsMfVWtOEb2XL18uGlNUVJQiGtunZu7cuUllA996kWFS0YsUhzOFQKVKlahYsWKm4notknaQct++fV4rWpzyMKnEgYP/WIkAzESiyw/H6yxEMPmAA4PwxuhlYVLxcu26XLb33nuPHnzwQbp165bLmsiTPbwwgmi9vKuYSUWe581zmsAXTqdOnTxXrkgKdOzYMUEqvXr1iiQZqeMyqUhdPeoqt2jRItF4du3apW4hbNK8ZcuWAhubknc9WSYV16vAmwqUKVOG8GGJj8C2bdsEqcQ+RBg/lLpXmFTUrTtpNf/ll19Eo5k5c6a0OrqtWK1atQgW8LwoTCperFWXy9S9e3fChrfo6GiXNZE3e23/zpw5c+RV0qRmTComgeNooRFIlCgRgVhYwiNQqlQpeuaZZ8IHUvAuk4qClSazynPnzhVDH/gWZgmPwJdffimwUvEkcriSMamEQ4fvGUagRIkSVLlyZcPx/BoB/oFgGsFLwqTipdp0uSwHDhwQb9558+a5rIk62X/yyScCs0OHDqmjdAKaMqkkABDf1o9A586dKWPGjPojcEi6ceMGPfzww4S9K14RJhWv1KQE5cD28969e0ugiVoqADNgp6LpyGBIM6kEQ4WvGUYAVs3QMI4ePWo4rt8jnDhxgrBi5hVCZlLx+xNtUfmfffZZz004WgSNrmTatm1LSZIk0RVW9kBMKrLXkAL6wbUneimwxcpiDoGdO3cKDMeNG2cuAYliMalIVBmqqtKuXTvKli2bqupLo3edOnUoe/bs0uhjVhEmFbPIcTyBwJ07d8QbduDAgYxIhAhovpHmz58fYUruRmdScRd/5XOfOnWqIJXffvtN+bLIUIDy5ctT8eLFZVDFtA5MKqah44hA4OmnnyZ021msQWD27NmCpFX25MikYs2z4MtUfvrpJ9EAVq5c6cvy21VoEDVMI6gqTCqq1pwEerdo0YLgdoLFWgSwAoTVNNilUVGYVFSsNQl0xvZyPPhwO8FiLQL//PMPPfroo4S9KyoKk4qKtSaBzhMmTBCkAj/JLNYjoLmKvXr1qvWJ25wik4rNAHs1+aeeeooaNmzo1eK5Xi6QddKkSQnkopowqahWYxLou3nzZtFL0eMXWAJ1lVWhY8eOlDx5cuX0Z1JRrsrcV7hx48ZUoEAB9xXxuAZ79+4V5P35558rVVImFaWqy31lcTwfE7RjxoxxXxkfaNCgQQPKlSuXUiVlUlGqutxXVlvu9LLbTvdR/leDdevWCRJfuHDhvxcl/8WkInkFyabe448/TtifwuIcArD5C8v7qgiTiio1JYGe69evF2/NDRs2SKCNf1TAAUMMObds2aJEoZlUlKgmOZSsX78+FS1aVA5lfKYF/AOpcsaKScVnD6fZ4p4/f168LSdOnGg2CY4XAQJYAUJv5fjx4xGk4kxUJhVncFY+l5EjR1LixInpypUrypdFxQLcv39fGHDC3hXZhUlF9hqSRL+sWbNS+/btJdHGn2oMHjxY9FZu3rwpNQBMKlJXjxzKaRbJoqKi5FDIp1pgCJoiRQqS3coek4pPH1Ajxa5duzaVLFnSSBQOaxMCXbp0odSpU9uUujXJMqlYg6NnU8HBNkwQTps2zbNlVKlgBw8eFPXxxRdfSKs2k4q0VSOHYkOGDKGUKVPSrVu35FCItaBGjRoRTonLKkwqstaMJHplypSJunbtKok2rAYQgP1a9B6XLFkiJSBMKlJWixxKLV++XDy8u3btkkMh1iIGgapVq1K5cuVi/sv0g0lFptqQTJfq1atTxYoVJdOK1QECixYtEoQP4+OyCZOKbDUiiT7w44Mu9qxZsyTRiNUIRKBYsWJUr169wMuu/2dScb0K5FQAeyHSp09P9+7dk1NB1oomT54siP/kyZNSocGkIlV1yKNMunTpqFevXvIoxJoERQAGnDp37hz0ntGL6J3279+f4CUxZ86c4hv7YmCYy4gwqRhByydhtfH6vn37fFJidYs5dOhQ0VuBT+tIBHWOF0mOHDmEsW3sS4LRbUwGM6lEgizHFQhUqVKFsLrAIj8Cf/31F6VJk4Y++ugj08r+8MMPgpiaNm1qOo3YEbmnEhsN/k1Hjx4VDxgMA7GogUCPHj3E/JdZbQsXLmzp8jSTitma8Gi8Pn36UJYsWTxaOm8WC+5RsVI3depUwwXUhrq7d+82HDdUBCaVUMj49DpOwWKyjkUtBJo3b0758+c3rDSGPJhHsVKYVKxEU/G05s2bJ954R44cUbwk/lN/69atou5WrFhhqPCYiLV6Zy6TiqEq8HZgLCXCzAGLmgjUqFHD8A7otGnTWu5alUlFzefHcq33798v3nTffvut5Wlzgs4gsGzZMlGHRs5qoZdSq1YtSxVkUrEUTnUTe/fddwk+fVjURgDGtBo2bKi7ECAU7E8xuhclXAZMKuHQ8dG9pEmTEmynsKiNwPTp00VvBca19Ih2xgtDX/zWBHtXYv/Xruv5ZlLRg5LHw+DQIJYkzT5EHodHueLlyZOHunXrpltvEAjmVvAMxP6YXWZmUtENvXcDwqUmHIGzeAMBuFMBOURHRxsqEEgEBINPJMKkEgl6HoiLBwkPoNGlSA8U3bNFuHbtmthhO3z4cFfKyKTiCuzWZ4qhC3wdGx3CwFRkvnz5rFeIU3QVgffee49gCtQNYVJxA3UL88SsPSbZ0NvAzkh8B066hcrun3/+EeHRXWbxFgJ4ueBZqFChgjCNsHnzZscKyKTiGNT2ZIQlwdjH00Eyevce4Hg7Hjy9KwX2lIBTtQOBTz/9VNQt6lf7YB+LE8Kk4gTKNuaBBwaHwmKLdkgs9rVgv2GO0Krj7sHS52vuIQAXHhqZaN+vvPKKIwoxqTgCs32ZYMjz9ttvx8kA/xM6JAaDyXjY1q5dGycu//EGAg899FA8UilYsKAjhWNScQRm+zLB8h/IAWb/MI7GCWPsOUhoj0HHjh2pSJEi9inGKbuKwJNPPhmPVLp37+6ITkwqjsBsbybacEfr5iZEKNevXxcP3Lhx4+xVjFN3HIHLly8TXKvgWcidO3cMsbz66qt09+5dR/RhUnEEZvsywWQrzm7AnijIBZO0+B/O9zH88CZKlIguXLhgn2KcsuMIbNu2jbCbFme4tA1ssOT3+++/O6oLk4qjcFubGYY7IJBRo0bFSRj/8aYKtWcF5gPbtm0bJw7/URuBL7/8UtQ57AufOnXK1cIwqbgKf2SZa/MpwVIBqQSuCiHcpk2bxMO3YcOGYNH4moIIwAQo6rtTp05SaM+kIkU1mFNCI5XAY+v4j4dM6wLHTr1NmzZUokSJ2Jf4t6II3L59m15//XVR12PGjJGmFEwq0lSFOUUwlMEqDowrYZs+vvEf1wMF7hxANhMnTgy8xf8VQ2DPnj1UqFAhevTRR6U7t8WkotjDFKgueiWa0ycQBiZq8T+w94J448ePJ+xfwAoBi7oIwH1KsmTJqGzZsvTrr79KVxAmFemqxD6FYG3dKheZ9mnJKYdDYPDgwaK32bJly3DBXL3HpOIq/M5lrs2/REVFOZcp52QpAo0bNxaEMmzYMEvTtToxJhWrEZU0vWbNmomhkaTqsVphEMBek+LFi4vtAwsXLgwTUo5bTCpy1IOtWpw7d0684cJtiLNVAU7cNAJLly4VZAJS2bdvn+l0nIzIpOIk2i7lhc1w2CR38+ZNlzTgbM0gMGLECPEyePPNN+nWrVtmknAlDpOKK7A7mynOgPTs2dPZTDm3iBDAfiKs5qnogpZJJaKqlz/yqlWrxMO5c+dO+ZVlDenkyZNi7gtL/7Nnz1YSESYVJatNv9JwLPXSSy/pj8AhXUMAtm0eeeQRgt2T7du3u6ZHpBkzqUSKoMTxcbAMXWj49WGRGwHN/GOdOnUIO59VFiYVlWsvAd3hoiFz5sx07969BELybTcRwIZEkH+vXr3cVMOyvJlULINSvoQee+wxwglWFjkRgD0bDE1BKFOmTJFTSRNaMamYAE2FKLCcjodVlb0NKmBqpY4wQZEzZ06C2UevmaFgUrHySZEoLRyJr1mzpkQasSoaAuiVgPBh3f7MmTPaZc98M6l4pir/Lcjx48fFQztv3rx/L/IvKRDAfiEQSqAHBCmUs0gJJhWLgJQpGZxkTchFh0z6+kEXGBuH8WkQClZ6vCxMKh6sXRjuGTBggAdLpmaRduzYIfxVZ8+enVavXq1mIQxozaRiACwVgmruOo4cOaKCup7XEbtiH3jgAapYsSJhWOoHYVLxWC3Dt3K9evU8Vio1iwMLfBjuwHPB/fv31SyECa2ZVEyAJmsU9E7wEMNOLYt7CERHR1ODBg1EXeCksd+EScVDNY43I5xJsbiHwIEDB+iZZ56hhx9+mJYsWeKeIi7mzKTiIvhWZ50hQwYaMmSI1clyejoRgFW2lClT0gsvvEAHDx7UGct7wZhUPFKnc+fOFd3tUF4JPVJMaYsBMsfQs2nTpr43hsWkIu1jakyxqlWrEgwjsziPQPPmzQWhYH8QCxGTigeeApzvwVtyxYoVHiiNOkXAEnHJkiUpVapUhJ4iy/8QYFLxwJPw/vvvC291HiiKMkVYuXIlYQ4Lk7K7du1SRm8nFGVScQJlG/PA/ofUqVPTyJEjbcyFk46NwOjRo0XPEPuBVDeoFLtcVv1mUrEKSZfS+eqrr8QDDitvLPYj0L59e4E326kJjTWTSmhslLhTuXJlatWqlRK6qqzk2bNnxVb7xIkT04wZM1Quiu26M6nYDrF9GWAsjwlaGExmsQ8BuIzNmjWrOBS4efNm+zLySMpMKgpXZI8ePahYsWIKl0B+1SdMmCCIGwavvGhQyY4aYFKxA1UH0rx9+zbBN8y4ceMcyM2fWXTt2lUQSvfu3f0JgMlSM6mYBM7taFOnTqUHH3yQzp8/77Yqnsv/8uXLVK1aNUEoEydO9Fz57C4Qk4rdCNuUftmyZalDhw42pe7fZKOioghuYmGU+vvvv/cvEBGUnEklAvDcirpt2zbxFv3xxx/dUsGT+WJVBxPfVapUoWPHjnmyjE4UiknFCZQtzgNGk8uUKWNxqv5ODruSQSgdO3b0lUElO2qdScUOVG1M89q1a8I8IY/1rQEZE95wNQpCwU5ZlsgRYFKJHENHUwCZYFs+JhNZIkNgz5499PTTTwun6MuXL48sMY4dgwCTSgwUavwoUaIEdenSRQ1lJdYSp1KdVpMAABbCSURBVIqTJk0qhpGw1sZiHQJMKtZhaXtKGzduFN30rVu32p6XlzMYOHCgwLFly5a+N6hkRz0zqdiBqk1p4jAbzvqwmEfgzTffFIQydOhQ84lwzLAIMKmEhUeem5cuXRKNAZveWIwjAE8DONKQLl06+uabb4wnwDF0I8CkohsqdwOOHz+eMmbMyN11E9UAq/Zp0qQRpLJz504TKXAUIwgwqRhBy8WwRYsWJTj3ZjGGwMcffyx6eA0bNiT09ljsR4BJxX6MI85h3bp1omHwW9YYlLAzg/0n8IfE4hwCTCrOYW06JzSO6tWrm47vt4gnT54US8XJkiUjWMZjcRYBJhVn8Tac259//inettw49EG3Zs0aypQpk9jUxgaV9GFmdSgmFasRtTi9Tz75hLJly0b37t2zOGVrkoPzsv79+8d84MfZLYdmsC2D4c5rr71Gp0+ftqaAnIphBJhUDEPmbISCBQtS7969nc3UQG6LFi0SDblcuXKEDxo1Pk7v+u3UqZPI99133zWgPQe1AwEmFTtQtSjN7777TjQUOAuTVXBiunDhwnHUGzVqlNDbiQnSCxcuCFMFILLJkyfH0YP/uIMAk4o7uOvKFX55cYJWZkHvBHoGCq5ho5mdgmMLOXLkEEaV2KCSnUgbS5tJxRhejoX+448/xNt+3rx5juVpJiP0ENAzCRStt2LX/Ap6JcgbPqTZoFIg+u7+Z1JxF/+QuQ8bNky8gUMGkODG7t27RcPGd6DArQUafbB7gWGN/n/nnXdE2hh6RUdHG43O4W1GgEnFZoDNJv/UU0/RgAEDzEZ3JJ7WGwmWWbh7wcLruXb9+nWCqwyQFY4tsMiJAJOKhPWydOlS0XAOHz4soXb/qoR5E8ypBBPcw3yHVbJjxw4C0WJ5fdmyZVYly+nYgACTig2gRprkG2+8QQ0aNIg0GdvjY9UHQ5BA+fvvv8UkbbB7gWH1/Nf8RVeoUIHYoJIexNwNw6TiLv7xcsekI7r32EQmu0BP7FMJlFq1alHatGkJ5BKp9O3bV+DRpk0bunHjRqTJcXwHEGBScQBkI1kMGjSIChQoYCSKK2G1idjYqzu4VqRIEUEokU7QYgK2Xr16glBGjBjhShk5U3MIMKmYw822WLly5aIhQ4bYlr5VCWNjG3oq5cuXFx/sScF/9FIiJRQMcUBOGTJkoAULFlilMqfjEAJMKg4BrSebhQsXioZ5/PhxPcFdDYNhD4gFH6z0oJcSu9diVjlYZUuePDm98MILxKYezKLobjwmFXfxj5N73bp1qUmTJnGu+enPRx99JEgVGLBBJXVrnklFkrrD8jGGD371P4MlaJQfc0osaiPApCJJ/fXr149gMtIPgmFejx49CI7RMNSDL6OUKVOyQSWPVD6TiiQViU1dI0eOlEQb+9SAmxH0SLRPkiRJxKTspk2b7MuUU3YUASYVR+EOntnXX39NaFynTp0KHsAjV48ePRpDJhqp4BvGqVm8gwCTigR1ifMssEPrdVm1alVQUsEBQRbvIMCk4nJd7t27VzQ02Fb1umASOnYPRfvdunVrrxfdV+VjUnG5ut977z0qWbKky1rYnz029CVOnFiQSqJEiWLI5cknnxS/4deYl5HtrwcncmBScQLlEHlgKzosv48dOzZECG9crl+/viCOhx56SKzwgDxgKhNzLBAY90avBatfbMFN/TpnUnGxDmfOnCmWUs+fP++iFvZm/cwzzwjCyJ49O8GaXSjZsGED5cuXT/Rm/LAKFgoHL1xnUnGxFmEKsUOHDi5qYF/WmCtCLww9kNKlS+vK6ObNm9S4cWMRB9/weWSlTJs2jV599dWY80rTp0+3MnlO6/8RYFJx6VHAuRY0uB9//NElDezLFlbZHnzwQVE+M5Owo0ePFnHhnmTlypWWKApjUjAapZ1Tgq0X4I//LNYiwKRiLZ66U+vevTvB6JDXpHnz5qKxJk2alCZMmGC6eNgM9/TTT4u0rDi1HezkNIjFbov/pgFQOCKTiguVd+vWLfrvf/8bUaNzQe0Es8TJYrz9M2fOTPv3708wfEIB7t69K9x/IE1M9oabk0korWD3NZswwe7xNfMIMKmYx850zClTpghbIZcvXzadhkwR0dizZs0qCOW5556zXDXNnSls1C5evNiy9NFTsdKOrmWKKZ4Qk4oLFVi5cuWgtl1dUCXiLLGCBfsn6E00bNgw4vRCJbB161YqVKiQyMcKLwOaHV1M3rJYiwCTirV4JphaVFSUaBhoJKrLW2+9JcqCTW3Dhw93pDgtWrQQedauXVuccDaTKQgFluVgpY7FegSYVKzHNGyKnTt3ppdeeilsGBVuVqxYUTTu9OnT05YtWxxV+dNPPxV5P/744zR//nzDecMLAD5WGOY2nLkPIjCpOFjJV69eFZvdpk6d6mCu1mZ17do1gh1dDHew5Hvv3j1rM9CZ2vbt20nbWNe7d2+dsUhM/DKh6IbLVEAmFVOwmYuEJdYsWbIo62oCk6SpUqWKGX6YQ8HaWDjdDYKrVq0aHTlyJGzisC7HhBIWIktuMqlYAqO+RMqWLUuqHvPHwUccBHzggQeEsWt9JXYmFMgaxIIVqFmzZgXNlAklKCy2XGRSsQXW+InibAsefBUtxFevXl3oDgdhVu1wjY9QZFewuQ0HEoFxIHFr+1FwL9gHHgFYrEOAScU6LMOm1K5dO0LjVEkwX5I3b17REPPkyUOYT5Fd2rZtK/R98cUXYzbgYUIWxBLqY4VrEdlxcVI/JhUH0L548SJh2zp8AqsiOJOEXb94s7/88suqqC30/OKLL8QwLWPGjMSHBp2vOiYVBzDHjlAsf2LbuQoC/zvYe4I5FFi9V1FwTKB48eKCFK1yFK8iDm7ozKTiAOo4E2Nk2dMBlUJmofkvxirP3LlzQ4ZT5YZmvR+nlIMdKlSlHCrpyaRic23BkhmGELAvIrtglyl0zZkzJ507d052dXXrh634GH5ionnSpEm643FAcwgwqZjDTXcs2F597bXXdId3I+CePXsI8w8gFLzRvSjYwwKnZSgjei8s9iHApGIftnT27FnxEM+bN8/GXCJLGgaV8Bb3S2Pr1KmTKCuGpNiVy2I9Akwq1mMakyJsrcLuqqyiGVRKkSIFTZ48WVY1LdcLJ6uTJUsmTld/9tlnlqfv9wSZVGx8ArAZy4pj+naoqA0F4G41oe3tduTvdprw4VyqVCnRa8EQ9c6dO26r5Jn8mVRsqkrsPMWQ4vDhwzblYC7Z2AaVnn/+eXOJeCgWTo2jnvACcPq0tYdgjFMUJpU4cFj3p0mTJtSgQQPrErQgpS+//FJ0+9GIoB/L/xCAL2sMAbE3Z8yYMQxLhAgwqUQIYLDoJ0+eFG+/RYsWBbvtyjVtghIOvdiCfPwqQA+uTJkyot7gHuTGjRvxA/EVXQgwqeiCyVigoUOHiiP2xmLZF1ozqPTII4/wikcCMMPLAXpysBXjRfcpCRTfkttMKpbAGDcR2FLFVne35fr16+J4ABoJDBqx6EPgm2++ibEbM2LECH2ROFQMAkwqMVBY82PJkiXizAxWF9wUGFTCPAEIpW7dum6qomTe8I5Yvnx5gR/mxrzi+cCJymBSsRhlPIBuT4L26tVLEBu8BA4aNMjiEvorOWAJYoZ7kLVr1/qr8CZLy6RiErhg0X799VfxAC5fvjzYbUeuwawiGgG23XMjsAZy9D5xbgi4WuEt0Rqt5E2FScXCuhk4cCAVK1bMwhSNJYW3KR58uAv9559/jEXm0GERuHTpEmkT3nXq1KELFy6EDe/nm0wqFtY+tuS7MbG3fv16SpMmjSAU9FRY7EOgT58+AmfYx5HVtKZ9pdeXMpOKPpwSDIUVA3jqO3XqVIJhrQyAVSYYo06SJAlh/M9iPwIgE80qHnqnLHERYFKJi4fpf+gS4wyJk/L666+LtyYe8IULFzqZte/zgg8nOIXDcLNmzZp05swZ32OiAcCkoiERwfehQ4fEw7VmzZoIUjEWFf5r8EBjHuWvv/4yFplDW4YADoyiHuAeBBO6LERMKhY8BX379hUnXi1IKsEkYFApQ4YM4kGGxXgW9xHAKtvDDz8s6gTPgt+FScWCJ+CJJ56gsWPHWpBS+CRgQBuH3vDBWR4WeRC4efOmcMGCXkvVqlXpxIkTppWDSxFMvgd+VLGxy6Riuur/F3HOnDmULl062226NmvWTLwJscozY8aMCLXm6HYhgIlzEAv2CWHy3ozApi7SCPyo4hWAScVMrceKU6NGDdttnmquJtAjYsdXscCX9CcOImbKlEmQAtzFGhWQh8q2gplUjNZ4rPCY38DbxK7TrOhC42Qx8gh8yEAuo0ePFudTcEalf//+TDix6sbtn/DxVLt2bVF3lStXpmPHjgmbxejZrl69Oqx6mIRXpVcSrCBMKsFQ0XkN+0LQoO0QDHFwdgd7UAKXqjG21ogGfoDxAengGlx7ssiDwMcffyzqJWXKlKIuUUf4lC5dmjAPE0xwH0MgVYVJxWTNwc/wY489RhMmTDCZQuhoHTt2FA8eHHphcjaYBJu0A7EE9miCxeVrziIAM5WYXNcIRfsO5hhecyaPXmjsiVpM3qoiTComawqmGTE0sbqytR4HCCsYcYRTV/WxeLiyqXTv1q1bhKHx/Pnz6cMPPyRsjNSIJPZ3MB/VsMoXO4z2W6UeKJOKyacVD4SV414YVMqePbt4oOCTxqiA3OBZ0EqdjOrgx/CY21q1apXoUb711ltily3OBWlkAJs28PwIM57aNe072LGKpk2bKt/bZFIx0RJ27NghHhCrrK9/++234qGDQ/RGjRrp1gjjbkzQdunSRSxrg1Cs7jnpVsbjAbFrOSoqitBDxaFC+JwGWWDeSyOJ3Llz0yuvvCLq4/PPPye4vIXtW8jEiRNjwiF8gQIFgm5DyJEjh5gjUxlOJhUTtdetWzeqUqWKiZjxo2hGgHAY0aitDm24gyETHkbsZWFSiY+xkSuYKzt48CCB6IcPH06tWrWismXLxiwRgxAw7MU13MNELKzs4ahGdHR02Kz27dsnrPV/9dVXdP/+/XhhUXdIXyaD6fGU1HGBSUUHSLGDYMYeD9XUqVNjXzb1G0MoPERZsmSJeFka3XAsReLtyaIPAZwoX7dunZhsx4uievXqlCdPnpgeBVbenn32WeFqBZOqs2bNEobDr1y5oi8Dg6G0SVrV9yIxqRiseLgHxdxHpC4c0FUGocCJlVWiPZRGJ3ityl/WdK5du0Y7d+4k7BHBAcA333xTGNPCcBN1gA/qA6QCa/oYqgDL06dPO1okEBd0wTaF2B/VlpeZVAw+NpUqVaJ33nnHYKx/g2OZEEvFeHhgusBK0UhF9TddJJj88ssvBHOeWEVp3749ob402yfAHGYh0WDbtm1L8HW9dOlSady+YtgDYgn8qFafTCoGnuCtW7cKMsBErRkZPHiwMEgN5+B4cMwKeiKBcyf4j8aCIZAf5Pz587Rp0yYxDMW81GuvvRbjjgTkgQ+GguiVoHeCXgp6K+i1sNiLAJOKAXyxZIgushnBQ48HHWdC8HaMRLS9DGg0WjcZhxpBKF4b+ty+fZv27t1LCxYsEL6UMBkNH0YaceAbtkxq1aolepCTJk0S81Nnz56NBGKOGwECTCo6wcPkHOyYzJw5U2eMf4Plz59fNAI4GcN+FCsE5IGxNno86DZ7gUx+//13cS5m/PjxBMfpFSpUiBkqgjySJk0qXJNiWANixTAHwx0WuRBgUtFZH9h3gFPCOCimV37++WexfwQNAiYHWf6HAIZq27ZtEwQNo0Y4eJctW7Y4vQ9YtINPY/gtmjt3riDNSCfHGX9nEGBS0YkznHf37t1bZ2gSRpuwJIm3a8+ePXXH81JA7NvA/g3s48B+jubNmwv3IbGHLunTpxdGjd59912aMmUKbdy4MeimMC/h4vWyMKnoqGGYNkBDwNhej2BXLMJjuDR79mw9UZQPg+VXrD598cUX1LVrV3EKFxPSsQkEy+c4LDlmzBjh3gLmAFi8hwCTio46xfIjJlr1CDZLoSHBB5DT7jr06BdpGMwJ7dq1i77++muxqoKJ68yZM8chDxyGxHI5DtPhUB0O1+GQHYs/EGBSSaCe4YkOJhwxrg8nMKgEE4IgFLhu8ILAjeuKFSuEMSj0vjQPiFrvA4fksPqEoQsmjTdv3sye+7xQ8RGWgUklAQBh0Bq9jnAyffp04cwLDr2waqGagDhBCCAGGNR+/vnn4xgUAolgBatFixbiNC5O5aq2IUu1OlFZXyaVBGqvRIkS4iRwqGAYGqHRYZ8IJhplFvhXxqE2GGTGSVv0qDBRqvU88I3eFoY0WHVBOIS/c+eOzMVi3SRDgEklTIXAnwsa2uHDh4OGKlmypLiPcyP79+8PGsatixiOwbkZfDvXr1+fcuXKFYc8UC70SNCzgulK7BZmp2Ru1Za38mVSCVOf6O43aNAgXgi4vMTJYjRMbNByUy5fvkw//fQT4aAjek3aRDF00z4wGoRywEQhiObkyZNuqsx5exwBJpUQFQzfuJiIDLRtAZ/FWCrFHpQ2bdqEiG39ZdjfQI8J29UxMVqxYkVKnTp1DHGAQHBQEQfo3n//faH3gQMHCPZBWBgBJxFgUgmBNoYNgYfzYHMDjReNOZRB6hDJGbqMcysYesFoE5ayNTOTWs8D3wULFqTWrVuLHgp2p6LH4pbgiAC7CHELffny9Q2pYLXCyIOPYQS8zWmCHgAaMyyswaygFYJt5zjxjCMAGGqBKGITB37DIBQOy0EXmCeUbe8LttzDNi50xeY3FkbAN6QCg8J48PUYvMHeDNgexY5PbDXXGk2pUqVMPzHY84Hj9+jtYMt/oCFkDKcw8YvdqNhYhqFOMJODphWwKSIIT8OWScUmkBVL1hekohkv0mtUGAfZ8EHPANbQYSGsSZMmuqr24sWLYgv6wIEDCS5R0dMI7H1gtQh2PjCEwiQrJn5VFMw3wegReivcU1GxBu3R2RekAsPQmusDfIcSNJJ+/fqJSVh8o6GAVIYNGxYvCvZuYBkWm+NAQHnz5o1HHmhwMJCNk7jLli0jTP56RTCcxN4crXfCpOKVmo28HJ4nFa2XgkYA2yOhPPjB321gjwLGf2AYGSdt4ZoBRpqwGS6YtzkYTGrXrp0YXsEau9cFOMb2McSk4vUa118+z5MKhjzaww9SwfxIoAT6ZNHIJbZtU+0aiAYrMui94PSyVUaXAnWS+T8MJAWujDGpyFxjzurmaVLBpKw25gesGN7g4Q8UWBLTSCP2N1ZjevToIU7aak6hAuP67T+Wj4FRoKU5XNOGQn7DhMsbF4H4LSzufWX/aUudGJZgKRkf2DfFwx94GA7kE5tMtN+XLl1Stvx2KY7VntiYatgCM+CL/yz+RsCzpIKhDnopGPvH/uDhD/ZGhUlDjUzwjc1vLPERiO0VMRBXDIlwjcXfCHiSVNBLwcoExv6BAsIItVcFZAMzBkeOHAmMxv8TQCAUWScQjW97EAFPkgreppigDSZ696oEi8vXQiPApBIaG7/d8RypYL4kXG8E3fNwe1X89gBYVV4MNwPnqqxKm9NRCwHPkQqGMHjAQwmGPqGGP6Hi8HVGgBHQj4DnSEV/0TkkI8AI2IEAk4odqHKajICPEWBS8XHlc9EZATsQYFKxA1VOkxHwMQJMKj6ufC46I2AHAkwqdqDKaTICPkaAScXHlc9FZwTsQIBJxQ5UOU1GwMcIMKn4uPK56IyAHQgwqdiBKqfJCPgYASYVH1c+F50RsAMBJhU7UOU0GQEfI/B/qFjolDW5r1AAAAAASUVORK5CYII=[/img][/size]

Two equilateral triangles are similar.[br]

An equilateral triangle and a square are similar.

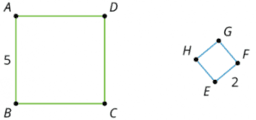
Find a sequence of rigid transformations and dilations that takes square [math]EFGH[/math] to square [math]ABCD[/math].[br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAdoAAADgCAYAAACkcqfQAAAgAElEQVR4Ae2dC4wcxZnHLQgk0Z3Pm0Qhd7m7rE8gBSHCbnRwOYVcdgMhARJlHY6XcMQ6QTkcEexcQnIiim59JuIOIp8fcCYGwjoQHAyyFwgkBgutscDB2Gb9CtjmsQaDbeLHmpffpk7/NjWMxzM9PTvd1dXdv5JaszvdXfV9v6+m/13VVdUjDAkCEIAABCAAgcQIjEgsZzKGAAQgAAEIQMAgtFQCCEAAAhCAQIIEmhLavr4+M2nSJNPf35+giWQNAb8I2Hqvul++zZ492wwNDfllLNZAAAKpExi20A4ODpoRI0YEW0dHR+qOYAAEXBFQfbd1v9rnD37wA1emUA4EIJABAsMW2u7u7tLFBqHNQKQxMTYCVlxthmrFqlenp6en9JuYOHGi3c0nBCBQcALDEtqBgYHggtLV1WXs3X3BOeJ+QQhIUCW0tW4u7X4do98JCQIQgMCwhNaKqy4q9m9QQqAIBKZOnRoIbViL1fb2hB1TBFb4CAEIHCbQsNDaO3Z7R2+FVt+TIJB3AlZEe3t7a7qqwVJhrd6aJ7IDAhDIJYGGhbatrS24iNhuMftcCqHNZf3AqQoCtv5rMGCtZG9GW1paah3C9xCAQIEINCS0uovXnbru6m2yQqtPEgTyTECDnlT/R40aFeqmFdp6x4Vmwk4IQCA3BCILrS4yo0ePDi405XfztpsMoc1NncCRGgSsgNrHJjUOC0Yg03Vciw7fQ6B4BCILrW25lrdmhSvqxad4aPE4bwTsb6DeTaUdMFVPkPPGB38gAIHqBCIJrVqzet6ku/RaW3t7e/US+BYCOSGg6Wyq/7q5DEt2gKAElwQBCEAgktBqmkItgS3/HpwQyDMBPXNVfdeNZ61UvmJa2HG1zud7CEAgfwTqCq29cOgiU+vC0draWvcClD90eFQkAvZ3oLoelmxrtvIRS9g57IMABPJNoK7Q2nmDYc+l7MWlXpdavlHiXZ4J2EF/YQJqfythN6V5ZoRvEIBAdQKhQmsHOtW7i7cXGF2MSBDIIwE7EKrac1fNKe/s7Ax6dSSydo55HjngEwQg0DiBUKG1LdWwVXBUpL0IhbV6GzeNMyDgDwH7Wxg3blzp1Xh6S48GAdpxClrMonzqmz/WYwkEIJAmgZpCa7vK6rVmZbxdyIK1XdMMJWUnScCKabVPjUamNydJ+uQNgWwTqCm06v5S13GUO3QNktKxdJlluzJgfW0Cqt+VW63BgbVzYQ8EIFBEAjWFtogw8BkCEIAABCAQNwGENm6i5AcBCEAAAhAoI4DQlsHgTwhAAAIQgEDcBJwL7YMPPmhmzJhhVqxYEbcv5AeBhgg88sgjZsqUKebJJ59s6DwOhgAEINAIAWdCq5HJxxxzTGkqhEZvfvGLXzQbNmxoxF6OhUDTBDRC+GMf+9gRdfEzn/mMWbp0adN5kwEEIACBSgJOhHbVqlVHXNTKp0h84QtfqLSJ/yGQGIGtW7eaD3zgA1Xr46c//enEyiVjCECguAScCO1VV11V9cJmBXfOgl+ZtduXssEg8Tow4afjQ+vi/Pnzi3s1wHMIQCARAk6E9pRTTgm9uH32239lvvXAx9lgkHgd+Ou2D4XWRa32RIIABCAQJwEnQmuXr7Mt2MrPi3/+efNfT17KBoPE68A/dp0YKrTTp0+P8/dFXhCAAASME6G96667Qi9uBw8eJBQQcEJg4cKFoXVx06ZNTuygEAhAoDgEnAitcH7ta1+reoGbNWtWcWjjqRcE9GKAyl4V/X/dddd5YR9GQAAC+SLgTGiF7c477zSfajvBjPzb480l4y5gLm2+6lKmvJk3b545pfPvzV/+zXGm45ufM48//nim7MdYCEAgOwScCq2w6FmsBj5plDEJAmkSsHXx3nU8l00zDpQNgbwTQGjzHmH8q0kAoa2Jhh0QgECMBBDaGGGSVbYIILTZihfWQiCrBBDarEYOu5smgNA2jZAMIACBCAQQ2giQOCSfBBDafMYVryDgGwGE1reIYI8zAgitM9QUBIFCE0BoCx3+YjuP0BY7/ngPAVcEEFpXpCnHOwIIrXchwSAI5JIAQpvLsOJUFAIIbRRKHAMBCDRLAKFtliDnZ5YAQpvZ0GE4BDJFAKHNVLgwNk4CCG2cNMkLAhCoRQChrUWG73NPAKHNfYhxEAJeEEBovQgDRqRBAKFNgzplQqB4BBDa4sUcj98jgNBSFSAAARcEEFoXlCnDSwIIrZdhwSgI5I4AQpu7kOJQVAIIbVRSHAeBZAkMDQ2ZRYsWmdmzZ5tJkyaZadOmBf/r+zwkhDYPUcSHYRFAaIeFjZMgEBsBCamEtaWlxYwYMaLq1tnZabIuuAhtbFWGjLJGAKHNWsSwN08EBgcHTXt7eyCuo0aNMhMnTjRTp041/f39pre3N/i/tbXVdHR0ZN5thDbzIcSB4RJAaIdLjvMg0BwBiaxtxXZ3d4e2WHVs1hNCm/UIYv+wCSC0w0bHiRBoioBaqeoqlsgWISG0RYgyPlYlgNBWxcKXEEiUgLqFJbLqFi5KQmiLEmn8PIoAQnsUEr6AQOIE2traAqGV4BYlIbRFiTR+HkUAoT0KCV9AIFECet6q1qwGPxUpIbRFija+HkEAoT0CB/9AIHECGlUc9mxWI441n7Z8y/rUHkFFaBOvWhTgKwGE1tfIYFdeCWgKj4S2p6fnKBcHBgaCfdpfvjHq+ChU9b+wF7e125fWP5gjIJAgAVsX7103PcFSyBoCELAE7Gjjas9nJagSYG1WkPPSxUyL1tYAPgtHAKEtXMhxOGUCVmjVRRyWtF+t2q6urrDDMrMPoc1MqDA0bgIIbdxEyQ8C4QSs0FbrOi4/U/trdTGXH5eVvxHarEQKO2MngNDGjpQMIRBKwHYJjxkzJvQ4tWQltPVavqGZeLQTofUoGJjilgBC65Y3pUHAdgnXE1E9m9UxeRhxrKgjtNT9whJAaAsbehxPkYBtrWqtY70WrzL19fUFIquFLfKSENq8RBI/GiaA0DaMjBMg0DQBtVKt2KrVqm306NGllwzY7/K0DjJC23S1IYOsEkBosxo57M4DAXUjS0w1QEqtV31q03NctWrz0m2sWCG0eaix+DAsAgjtsLBxEgQg0CABhLZBYByeHwIIbX5iiScQ8JkAQutzdLAtUQIIbaJ4yRwCEHiPAEJLVSgsAYS2sKHHcQg4JYDQOsVNYT4RQGh9iga2ZJHA/PnzzRVXXGEuvfRSc9ddd2XRBSc2I7ROMFOIjwQQWh+jgk1ZIHDw4EFz1llnBVNz7HQcfba3t5tNmzZlwQWnNiK0TnFTmE8EEFqfooEtWSJw7bXXHiWyVnAvv/zyLLnixFaE1glmCvGRAELrY1SwKQsEjj322JpCK8HdtWtXFtxwZiNC6ww1BflGAKH1LSLYkwUCGzduDBVZCe3ixYuz4IozGxFaZ6gpyDcCCK1vEcGerBD44Ac/GCq2e/fuzYorTuxEaJ1gphAfCSC0PkYFm3wnsOXtfeaUSybUFNpLv/Nvvrvg3D6E1jlyCvSFAELrSySwIysE1mx723z1jmdMx/8tNZ/43FeOEtu/OPmfzDm3PGG2vrM/Ky45sROhdYKZQnwkgND6GBVs8pXA717YYc765bJAZC+5b63ZueeAWbJkifnZz35mfvzjH5vfP/Ko0fcS4QvnrjF7Dhzy1RXndiG0zpFToC8EEFpfIoEdvhP4xVOvBgIqEb16wfNm/6F3q5q8ffd+c/6vB4Jjxz+8wVQ/quqpuf4Soc11eHEujABCG0aHfRAwZveBQ+Z7v99QEtmblm+ui2X9zt3m7FuXB+fc+BSLVwgYQlu32nBAXgkgtHmNLH7FQUCDni747epAMM+etcwseGln5Gz7X95lOmcuDc5Vl3PRE0Jb9BpQYP8R2gIHH9dDCQy8/v6gp/NmD5jnduwOPb7azlkDWwKh1XNd5VfkhNAWOfoF9x2hLXgFwP2qBNQC/dItTwciedHctWbb7uGPIP7RwheDfDRS+bW39lUtrwhfIrRFiDI+ViWA0FbFwpdNENCqSKNGjQrNobe3N5gWM3HixNDj0tipZ6oa8KRNz2b3Hmxu5LAGTY2d/2yQ3zfnrDZv7z+Yhlupl4nQph4CDEiLAEKbFvl8ltvf3x8IaEdHR6iD3d3dwXF9fX2hx7ncWTnoacrSV2MrftfeA+brd60MxPaK360zNQYsx1aejxkhtD5GBZucEEBonWAuTCE9PT2BgOozLLW1tQXHDQ4Ohh3mbF/5oCd1GScxeOnFoT3my7cdHon88ydeceabLwUhtL5EAjucE0BonSPPdYFdXV2RWqpRupddgSof9PSVX61IdNDSk6++URqJPG/9dlcuelEOQutFGDAiDQIIbRrU81tma2trILRDQ0M1nbTdyxLltFP5oCdN43ExWKl39etBF7Jazk9vfjNtBM7KR2idoaYg3wggtL5FJLv2qBtYLVWJbViK2r0clkez+7Ra0w1/fH/Q03cfWh8sTNFsvlHPv7Z/MBDbc25fYV5+oxhv+UFoo9YOjssdAYQ2dyFNzSENbJLQ1mup2u5ltWzTSBr0JGG1I4uvX/KK82USD777rum+/7nAhq67V5k396U/ElnxWLRoUc2t2efpCG0atZ0yvSCA0HoRhlwYYVuqo0ePNp2dnTW3lpaWut3LSQFR17Bd6Uldt/NTfE4qcZXISvAluhLftJK6+nWTFLbVG+BWz3aEth4h9ueWAEKb29A6d0xTesIu1OX7NOrYddKgJw12krCpy3bZlvSfj6rbWLbIJnUnp5Xsc3PFRYJabaNFm1Z0KDfzBBDazIfQGwe0SIXENCzZ7mXNo3WZygc9feM3q8wrb/rzXFQDojpnHl6Favaa111iKZVleyOabbWWMqzyR3jNqHJCs1/Zi9va7UubzYrzIdAUAVsX7103val8OLnYBAYGBgKRrddStRf0qVOnOgFWOejp2w+s8+J5aKXzc/7056BVK8HVFCDXyfZGJPncHKF1HVXK84YAQutNKDJtSNQlFV1c0C3IykFPkxa/7PWKTNc98XIgtlrUQotbuEy2NyJsWlaz9iC0zRLk/MwSQGgzGzqvDNeaxeo2luCGJfucNuyYOPaVD3pSK3Huc9viyDbRPLQso5Zn1PNaLdeoZRtdpKjTspq1BaFtliDnZ5YAQpvZ0HlluF1SUV3ItZLtXq63DnKt86N+Xz7oSa3DJa+574qNamvlcXrhgF48ILHViwj0QoKkk6vn5ght0pEkf28JILTehiZThkVpqUbtXm7GcU3Xsa+3+/qdK81Lu9x2wTZjuz1XrXG9Uk9iq1fsJZ1sb8S4ceOqzqFtdrSxtR+htST4LBwBhLZwIY/dYTs1pF5L1V7Q63UvD8dAtfv+Z8n7Kz2Nnfess67X4dhb7xy1yu0Ng14en2Syz83tzVLlZ1xvWEJok4wieXtNAKH1OjyZME4jiHVxrjc1xF7Q42ohWTiVg55+8thL5oCDLldbflKfeumAWrWdM5ea/pd3JVVMEDsbP8WwcosrXpGEVs8XwpanCns2UUnIXtyY3lNJhv9dE7B1kek9rslTXhwEjhz0tNTctnJrHNl6k4ddj/nsW5eb9Tt3x26XfW5eb1pWHAVHElp7N1bZrLb/1+s2KTfUXtwQ2nIq/J0GAVsXEdo06FNmMwTKBz1JiBZvSq7V14ydzZyrLvHxD28IWrbn/3rAbN+9v5nsjjrX9kaoWz/pFElo7ai6yma1/b+R5w724obQJh1a8q9HwNZFhLYeKfb7RKB80JME6PkEWnu++LvnwCFz4dw1gdhect9as+/godhM0wpdaiw2ol/DLTyS0MqYuJrX9uKG0A43ZJwXFwFbFxHauIiST5IE1ML77yWvBKKj55cSnp173Mw3TdKvenlvfWe/Obf38Ejkqxc8X+/wyPttA7KRR5+RM684MLLQNtI9XFHGEf/aixtCewQW/kmBgK2LCG0K8CkylMCDDz5oxo4da8444wxzzTXXmBWr1x7xejsJjot5pqFGOty5dts75qxfLgtuMm5avjmWku2jz1gyq5MJQlsHELvzSwChzW9ss+zZZZddVhoNa8VAnyde9tNAaG5eEY/QZI2RXo6glry2RwZ3NmV+1GlZTRVSdnJdobUGxfXA2F7caNGWRYE/UyFg6yIt2lTwU2gVAvPnz68qslZwH1qfzhtuqpiayldTn34tENqzZi0zauUON0nXNMZIny5SZKGtfJnxmDFjzLRp00yjCzHbixtC6yK8lBFGwNZFhDaMEvtcErj44otDhfbuu+92aY6XZanbXK3a82YPmNffiXckclIO1xVaPSi2bzfQXVXlVJ+WlpaGRm3ZixtCm1RIyTcqAVsXEdqoxDguaQKnnXZaqNCqFVb0tPfgoWAgmMT24nvXGo1M9j3VFVo5UG11DLVkFXTbpRG1CW4vbgit71Uj//bZuojQ5j/WWfHw6quvLl1T7bW1/HPhwoVZcSVRO//8zn6jqU0S2+//Ib6RyEkZHUlowwq3a3hqTlKUZC9uCG0UWhyTJAFbFxHaJCmTdyMEVq5cWVNoP3nSyY1klftjg5HIsw6PRJ6y9NXA371795o33vDvjUVNC60dLNXe3h4psPbihtBGwsVBCRKwdRGhTRAyWTdM4JZbbjlKbI//5Inmsz/pNQsHhxrOL88naPSxWrVtP7rd/PM555e4nXDCCeahhx7yxvWmhVZdyOra0HPcKMle3BDaKLQ4JkkCti4itElSJu/hENi3b5/RwKfJkyebxx57zPziqVdLo22f3T780bbDscX3c66Z/UBJYMu72fX33LlzvTC/aaG1LdqoC1rYixtC60X8C22ErYsIbaGrQSac16pQVz68PhBbrZKUldG2LuBqBkylwNr/jzvuOBcm1C2jaaG1o5C1QHOUZC9uCG0UWhyTJAFbFxHaJCmTd1wENLpWyy6qq1SfWRhtG5fvtfLRM1krqrU+161bV+t0Z9/XFVoNctJ82cr1IPW/vZPQmpFR59PaixtC6yzGFFSDgK2LCG0NQHztHQG1ZO1o2zjX/fXO0YgGvfXWW3WFds2aNRFzS+6wukJrW6y17ha0P6rIyg17cUNokwsqOUcjYOsiQhuNF0f5QUDPaLUyklq2enZb9PSRj58QKrY+8KkrtBJRvUZI03gkqnbT/1HnzpY7ai9uCG05Ff5Og4CtiwhtGvQpsxkCGn0sodX28As7mskq0+fOWPaaOfX7M2oK7e233+6Ff3WFNm4r7cUNoY2bLPk1SsDWRYS2UXIc7wOBWQNbAqHVW21Wvv62DyY5s0FvLrJLMXbOXGrG/+8dZuTIkUcIrov3zEZ1GKGNSorjckcAoc1dSAvn0L8/+kIgtl/51Qqz+a19hfBf7+C1g8LOnrXMPLbx/bnFGzduNOvXr/eOA0LrXUgwyBUBhNYVacpJioBadpfN+1MgtmPmrDbv7Pd/3d9mWDy3Y3dpMJheKqD/s5AQ2ixECRsTIYDQJoKVTB0T2LX3gPn6nSsDsf3Og+vMIU26zWFSy1UtWD2XvmjuWrNtdzbe3KNQILQ5rJC4FI0AQhuNE0f5T+ClXXvMl29bHohQz+KN/hvcoIV6Hq1nsRJZPZvVG3yylBDaLEULW2MlgNDGipPMUiaw5LU3TOfMpwMxmvvctpStiaf4A4feNT9c+GLgk0RWL37PYkJosxg1bI6FAEIbC0Yy8YiABFaCJMGV8GY5qUt87LxnA380snrBSzsz6w5Cm9nQYXizBBDaZglyvo8Efv7EK4E4qStZXcpZTLLbPnf+6h3PmDXbsj19CaHNYi3E5lgIILSxYCQTzwhoMJQGRallK7FSyzBLafGmXaXnzRf8drXZ8nb2py0htFmqgdgaKwGENlacZOYRAU3z0XQfia2m/2gaUBZS7+rXS8+Zv/vQerP7QLYGPdVijNDWIsP3uSeA0OY+xIV2UAtYaCELia0WtvA5HXz3XfOTx14KbJW9N/xxk8nGrUE0qghtNE4clUMCCG0Og4pLRxDQ0owaSCTxumn55iP2+fLPm/sOmsv7ngts/NItT5v567f7YlpsdiC0saEko6wRQGizFjHsHQ4BvXRAQqtNLyPwKb3y5l7zjd+sCmxT63sgp2s2I7Q+1TpscUoAoXWKm8JSJDBt2WuBmOn1enrNng9p2ZY3zTm3H+7a1vPk13K8VjNC60ONw4ZUCCC0qWCn0JQIfP8Pzwdie27vM0YvkE8zqXtY3cRqZX/7gXXm7f0H0zQn8bIR2sQRU4CvBBBaXyODXUkQ2HfwUOmtN/96zxqzJ4URvRr8bOf5SmQnP/FybtdmLo8hQltOg78LRQChLVS4cdYYs2PPgdLbb658eL3Tkb1qtar1KoHVylV5WSYySsVCaKNQ4phcEkBocxlWnKpDYMPO3ebsWw+PRL5+ySt1jo5nt56/2nm9ei6b9eUhG6WC0DZKjONzQwChzU0ocaRBAo+/sqv0Npy+DTsaPLuxwzWS2M7n1QhjjTQuWkJoixZx/C0RQGhLKPijgATuWLU16MbVoKTlW95KhMDvXthRGvSkubKaM1vEhNAWMer4HBBAaKkIRSdgV2NSd27cLc0bn9oUCLmeyaocrf5U1ITQFjXy+G0QWipB0QlI/OyqTOrWjaPFqfWJv/f7DaVBT2o5Fz0htEWvAQX2H6EtcPBxvURA4mpXZ5LoNtPy1Jt29MYdtWLPvnW50Zt4SMYgtNSCwhJAaAsbehyvIKBuY7tKk7p5h5P0zli9O1Yie/6vB8zzO3cPJ5u65wwODpr777/fTJo0yUybNs0MDAzUPSftAxDatCNA+akRQGhTQ0/BHhLQgCi7WtNtKxvr7l3w0s7SywvGznvW7NwT/ztwJaidnZ1mxIgRR23t7e1eCy5C62GFxyQ3BBBaN5wpJTsENNXn8IISS42mAEVJ099bR1nn/XDhi+ZAAu++lchage3u7jZ9fX2mv78/2Lq6uoJ9LS0tZmjIr5cmWH4IrSXBZ+EIILSFCzkORyCgd8Eefsa6zGhxi1pJL5O/esHh9ZM7Zy41tzyzpdahsXzf09NTs9VqxVbH+JgQWh+jgk1OCCC0TjBTSMYIaBKOlme0z1q1bKNaisuXLy95oq7hS+5be1iQZy0zj21MtyWpFq5avB0dHSUbffoDofUpGtjilABC6xQ3hWWIgF44oBcPnP6f95q/+/y5pW5bidn4H/1Hab3k82YPmOd21G71unJZ3cgIbRlte3Fbu31p2bf8CQH3BGxdvHfddPeFUyIEPCfw8o43zXEfOeEIkbXPST96xrnmorlrzbbd6b5uzyKcOnVqYCddx+8RsRc3hNZWET7TImDrIkKbVgQo12cCN9xwQ1WRtWL7zKrV3pjf2toa2KqpPz4muo59jAo2OSGA0DrBTCEZJXDmmWeGCu2UKVO88My2ZjUgyteE0PoaGexKnABCmzhiCsgwAQ0ssq3Xap833XRT6t7ZZ7Nq0fo6tUeQENrUqwoGpEUAoU2LPOVmgYCEtJrA2u9eeOGFVN3Q3FrNnR01alTNaT+pGlhWOEJbBoM/i0UAoS1WvPG2cQKnnnpqVbGdOHFi45nFeEaWRFZuI7QxBp+sskUAoc1WvLDWPYEdO3aYCRMmmGOOOSYQ3JEjR5oZM2a4N6SsxKyJrExHaMsCyJ/FIoDQFiveeNscgc2bNzeXQQxnZ1Fk5TZCG0PwySKbBBDabMYNq4tJIKsiq2ghtMWss3htDC9+pxZAICMEsiyyQozQZqSiYWb8BGjRxs+UHCGQBIF6U43sSGh9+rg6FEKbRK0gz0wQQGgzESaMjIFAb29v8KJ0vSy92qb9PieNcpbYRtl89AWh9bl2YVuiBBDaRPGSuUcEylt81f5Oe7qOR6gSMQWhTQQrmWaBAEKbhShhY7ME9HxT4trW1lZ6Wbp9abr99HWN4GZ99+V8hNaXSGCHcwIIrXPkFJgCAXWlSmhptaYA/70iEdr02FNyygQQ2pQDQPFOCHR3dwdC6+OzSycAPCgEofUgCJiQDgGENh3ulOqWgLqM1aJVFzIpHQIIbTrcKdUDAgitB0HAhMQJSGS18D4pPQIIbXrsKTllAghtygGg+MQJ2NfItbe3m0WLFh210cpNPARBAQitG86U4iEBhNbDoGBSrAS0eINatLU2Pb8lJU8AoU2eMSV4SgCh9TQwmBUbga6urkBkJagS3cpNLV5S8gQQ2uQZU4KnBBBaTwODWbERaG1tDYSWebKxIR1WRgjtsLBxUh4IILR5iCI+1CIwNDQUiKzElpQuAYQ2Xf6UniIBhDZF+BSdOIG+vr5AaNV9TEqXAEKbLn9KT5EAQpsifIpOnIAdCKVPUroEENp0+VN6igQQ2hThU3TiBOyr5RjwlDjqugUgtHURcUBeCSC0eY0sfomAFqnQtJ5q82f1HQOk3NUThNYda0ryjABC61lAMCc2AhLRWnNn7fesfRwb7roZIbR1EXFAXgkgtHmNLH5JaCvnzFb+T4vWXT1BaN2xpiTPCCC0ngUEcyCQUwIIbU4Di1v1CSC09RlxBAQg0DwBhLZ5huSQUQIIbUYDh9kQyBgBhDZjAcPc+AggtPGxJCcIQKA2AYS2Nhv25JwAQpvzAOMeBDwhgNB6EgjMcE8AoXXPnBIhUEQCCG0Ro47PAQGElooAAQi4IIDQuqBMGV4SQGi9DAtGQSB3BBDa3IUUh6ISQGijkuI4CECgGQIIbTP0ODfTBBDaTIcP4yGQGQJOhXbevHnm1LM/ZT564vFm3FVjzbp16zIDCkPzRWDBggWm7dx/MB/5h+PNVy/7F7Ns2bJ8OYg3EICANwScCe2FF15YdZHr2bNnewMDQ4pB4Morr6xaF2+88cZiAMBLCEDAKQEnQnvPPfdUvbDpLRLHHnusU4cprNgE9How+/aSap9bt24tNiC8hwAEYifgRGg7OztDL26XXH+m0fMyNhgkXWe2R/cAAARnSURBVAfOuOCk0Lp48803x/4jI0MIQKDYBJwI7cknnxx6cfts90jzrQc+zgaDxOvAJ077UGhdnDBhQrGvCHgPAQjETsCJ0I4fPz704jZ5zkRz77rpbDBIvA5cdPV5oXXxvvvui/1HRoYQgECxCTgR2uXLl9e8uJ1++unFjgDeOyWwadOmmnWxtbXVqS0UBgEIFIOAE6EVypkzZx51gZPIrlq1qhik8dIbAnfffbf58Ic/fER9POmkk4wGSpEgAAEIxE3AmdDK8L1795o5c+aY66+/3ixevDhuX8gPAg0RmD9/vpk8ebJ59NFHGzqPgyEAAQg0QsCp0DZiGMdCAAIQgAAE8kAAoc1DFPEBAhCAAAS8JYDQehsaDIMABCAAgTwQaEhoBwYGggEjGjSibXBwMA8M8AECEIAABCCQGIGGhHbUqFFHjNS0S9i1tLSYSZMmmaGhocQMJWMI+Eigt7fXaOUz/QbKfw/jxo0z/f39PpqMTRCAgGMCkYVWrVldSDTXsKenJ9gmTpxoOjo6SheY9vZ2x+ZTHATSIaDfw+jRo0t1v62tLfgt6Peg34h+K/qdkCAAAQhEFlrduevi0d3dfRQ1dSHb1i538Ufh4YucEejr6yu1YPV7qPYIRb8DenhyFnjcgcAwCUQWWrVeJbRTp06tWpQuONzFV0XDlzkiIFG13cS6+SRBAAIQqEcgstCqa0xCqi6zaskKbS0hrnYO30EgawTsoxLdeJIgAAEIRCEQWWglstqqJXWR2bv8at1o1c7hOwhkjYC6g/Ub0GMSuoWzFj3shUB6BKorZ4U99gKju/nKpH0aBKULEF1plXT4P08EbK8Nrdk8RRVfIJA8gUhCq+5g26Kt9tnV1WU0QIQEgTwTsAP+aj0+ybPv+AYBCAyfQCShtXfy5VMY7DNbdRlrziBdacMPAmf6T8BOb9ONJgkCEIBAIwQiXTXsvMDK568SVyvCzKFtBDvHZo1A2OOTrPmCvRCAgFsCdYVWYqq7eHWb1Uq2dauLEQkCeSSgRyP6HVQbp5BHf/EJAhCIj0BdobV38noOWyvZKQ+shFOLEN9nnYD9HdBzk/VIYj8E3BOoK7QST93Jh4mobdEyIMp9ACnRDQErtDyjdcObUiCQJwJ1hda2Vmt1C5dfgBgQlaeqgS+VBOyoYxZlqSTD/xCAQBiBukJrLy6VIqr/9cYeu1BFWIs3zAD2QSArBGzvjuo8U3yyEjXshED6BEKFVqOM1VVWb0Nk0w8kFrghYB+T6DcxZsyY4GZTN5ya4qbntwyWchMHSoFAlgiECq3u2nXhqLZpWo+60CpbullyHlshMBwCurG0PT3lN6H6jpvO4RDlHAjkm0Co0ObbdbyDQHMEdCOqMQra6EpujiVnQyDPBBDaPEcX3yAAAQhAIHUCCG3qIcAACEAAAhDIMwGENs/RxTcIQAACEEidAEKbeggwAAIQgAAE8kwAoc1zdPENAhCAAARSJ4DQph4CDIAABCAAgTwT+H9GlNskBX+PrAAAAABJRU5ErkJggg==[/img]

Select [b]all [/b]true statements given that angle [math]AED[/math] is congruent to angle [math]ABC[/math].[br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAPsAAACnCAYAAADXPioqAAAYtUlEQVR4Ae1dCdQO1RvnL4qIkC1bvsiuopTTYjkkp6QUHaUs2dKCKBVaLF+ILPmiKEsHKaWolJMsiQplJ5IklBJJi+35n9/t3NeYb+b95v2+OzP3zjzPOXPeeWfu3Pvc33N/c5e597m5iIURYARigUCuWOSSM8kIMALEZOdCwAjEBAEme0wMzdlkBJjsXAYYgZggwGSPiaE5m4wAk53LACMQEwSY7DExNGeTEWCycxlgBGKCAJM9JobmbDICTHYuA4xATBBgssfE0JxNRoDJzmWAEYgJAkz2mBias8kIMNm5DDACMUGAyR4TQ3M2GQEmO5cBRiAmCDDZY2JozqY/CDz11FP09NNPJ44lS5b4k5CCWJnsCkDkKOKJwO+//065cuWiOnXq0PXXXy8O/K9YsSLhnm7CZNfNIqyPMQi88847guzff/99QmecFy5cmFDj6yZMdt0swvoYgwAIXaFChUz6oqa/9957M10P+wKTPWwLcPrGIoCm+y233HKG/l9//bWo7V977bUzruvwh8mugxVYByMRQHO9YcOGicG5Xr16UZEiRbRswgNgJruRxYyVDhsBWYPbB+dAeF2Fya6rZVgvrRFAMx0j71aRg3MPP/yw9bI252dqq41arAgjoDcCIDRqdbu4XbeHC+M/kz0M1DlN4xHA4JxTDS6/t+uYQSa7jlZhnbRHAE14+4j7Cy+8IJr2+P6uozDZdbQK66Q1Ap9++qkg9aWXXipG4/EL8us6mUaCyWSXSPAvI+ARAUyFBeHth8fHQwvGZA8Nek6YEQgWASZ7sHhzaoxAaAgw2UODnhOOGwKzZs2iDh06UJ8+fWjt2rWBZ5/JHjjknGAcERg4cKAYxMNAnjxWrFgRKBRM9kDh5sTiisC5556bILkke9Ar45jscS19nO/AEPj5558zER2Eb9KkSWA6ICEme6Bwc2JxQyA9PZ3y5s3rSPYRI0YECgeTPVC4ObG4IAAi58+fX5Ack24GDBggJt3IJnynTp0Ch4LJHjjknGCUERg9ejQVLFhQkLx27dqUkZFBp06dovXr14trL774Ih04cCAUCJjsocDOiUYNgbFjxwrHFai5a9asSSD1iRMnEtns37+/qNkTF0I4YbKHADonGR0EJkyYQMWKFRO1dvXq1WncuHF07NixTBksX768+L6e6UaAF5jsAYLNSUUHgYkTJ1LJkiUFyatWrUpjxoyhv//+2zGDs2fPFuE2b97seD+oi0z2oJDmdCKBwOTJk6lMmTKCvJUrV6ZRo0bR0aNHk+atZcuW1KBBg6RhgrjJZA8CZU7DeASwdh1NcfTJ09LSaOTIkXTkyJEs87Vt2zbxzJQpU7IM63cAJrvfCHP8RiMwY8YMqlSpkiDsRRddRMOHD6fDhw97zhN8y+M7uw7CZNfBCqyDdgjMnDmT0ExHTY6NIDA5JjtbOiGOLl26aJE/JrsWZmAldEFgzpw5VK1aNUHycuXK0dChQ+m3337Llnrz5s0T8axatSpbz6t+iMmuGlGOz0gE5s6dK76PoybHANzgwYNzPPnljjvuoFq1ammDB5NdG1OwImEg8O6775L0IYdPadh+ef/+/TlWZdeuXaJWxyc5XYTJroslWI9AEViwYAHVrVtXELJ48eI0aNAg2rt3rzIdhg0bJuL2MmKvLNEsImKyZwEQ304dAbhSRg3pJtg6CR5bsE8afvE/KFm4cCHVr19fEBH7smGByp49e5Qnjymzd955p/J4cxIhkz0n6PGzmRDApyb0e3E4iXTDjM0UEBa/IJ3fhF+0aJGY2AK9ChUqRE888QTt3r3bScUcX/vwww9F/pGmTuJsEZ00ZF2MQACfpVBTY0skuVmCk+L4jGXf5hj/8awfgpfLddddJ8hXoEABwoIU9Kf9lPbt2xO+yesmTHbdLGKwPqippU91p5odGx/iOghoFVnb474qWb58OTVq1Eikd/bZZ9Ojjz5KO3fuVBW9azz79u2jPHnyiNF810Ah3WCyhwR8lJOV5LXn0e06wjm9BOzPe/n/+eefU9OmTUV8Z511FvXt25e2b9/u5VElYTBXHnlROdinRDF2S6UKRo7HioAbqZM170EQtAyyK19++SU1b95cEC137tzUu3dvwrz0oAUj/C1atAg6WU/pcc3uCSYOlAoCbmSXg3dOcWWX7GvWrKGbbrpJkBxxYGfVLVu2OCXh+7XFixcLPd5++23f08pOAkz27KDGzyRFwI3sWDkGQjoJrqPm9yrr1q0TA314DseDDz5ImzZt8vq4L+Huu+8+KlWqlC9xq4jUGXkVMXMcsUXAjezyun1BCf6DsLiflWzcuJFat24twuOZnj170oYNG7J6zPf7Bw8eJPiG79evn+9pZTcBJnt2kePnXBGQpHYKAILa9y+XNb79JWB9fuvWrdSmTZsEyXv06EGo3XUR+JxD3sIYJ/CKAZPdK1IczjMCyciOXVAwF10SG7/477Y7CkbS27VrlyB5t27dfJ+A4zmjloDwRHPttddaruh3ymTXzybGa5SM7CA3Jt6gFsREGvzivyS/zDy+ud9zzz0JkqM/vHr1anlbq1/s2YZ8TJ06VSu97Mow2e2I8P8cIwDiZtX/xn003+3hMIW1Y8eOCZJjMwV8VtNZMG5QuHBhnVUUujHZtTdRPBTEJBR4dEENiQMLZHRx+pDMAn/99RcVLVqUunfvniyYFveY7FqYIb5KYNNDEEWSHE13zIIzRV555RWh+1dffaW9ykx27U0UTQXh6umBBx5IkPzuu++mzz77zLjMNm7cmOrVq2eE3kx2I8wUHSUPHTokZrnJmhwj7cuWLTMygxgwRD7Gjx9vhP5MdiPMZL6Sf/75Jz3yyCOJmhyOHeyDc6blsk+fPpQvXz5Cv90EYbKbYCWDdcSWSFheKmtyOGH85JNPDM7Rf6qfPHmSSpcuTXfddZcxeWGyG2MqsxQ9fvy48AYjSX7bbbeRbp5bcoLo9OnTxQsMi19MESa7KZYySM+BAwcmanJ4ofnoo48M0t6bqjfeeCPVqFHDW2BNQjHZNTFEFNR45plnEiTHslP4YouiYOENWizwIGuSMNlNspamug4ZMoTgFQYEQI33/vvva6qpGrUef/xxkVfMETBJmOwmWUszXZ977jmCfzeQvFmzZjR//nzNNPRHHTiTvPXWW/2J3MdYmew+ghvVqLFdMdZug+RNmjQh7GkWF8FecMg3dpIxTZjsplksRH3hSea8884ThR3+3nV1v+QnRK1atRJbOPuZhl9xM9n9QjZC8Y4bN04s9kCNds0119Bbb70Vodx5z8q3334rXnTos5soTHYTrRaQzhkZGXTBBReIAn711VcTmrBxFmxphRfejh07jISByW6k2fxVetKkSWJ2GAr2lVdeSbNnz/Y3QUNir1q1qnBXbYi6mdRksmeCJL4XpkyZQmXLlhW1F/yfz5w5M75g2HKOATm8/F5//XXbndN/4V0HWzSjBYBD5Q43p1PJ/hmTPfvYRebJadOmUcWKFUVhhj+4GTNmRCZvqjLStm1b0dpxiw/+6vEywMAlznH4vVmlmy5u15nsbsjE4DpqqbS0NFFIa9WqRSA9S2YEfvjhB4ERfNM7Cb5SwC2V3WuuU9gwrzHZw0Q/pLTRB7/kkktEAa5WrZrwBReSKkYkm56eLrByq6lB9FQ2uAgr00z2sJAPId0333yTqlevLgpulSpVCH10lqwRgPdbbPvsJFiTj+a73TuuU9iwrzHZU7QABl3kAIz1V+cmHHSrXbu2KJRotsNvGos3BBYuXChww2dIJ8H+dajZQXrpGhvjHigbugmTPUWLSONiIMZ6wC2ybvLee+/RZZddJgorBuDwSY0lNQSweUWRIkXo2LFjjg+iPABblAW8VNHUxy9eABik00mY7ClaA0bFGm2d5YMPPqArrrhCkLxcuXL00ksv0alTp3RWWUvd9u/fLxb6YIMKN5E709qb8XJLK7fnwrjOZE8RdbyxYWAdBU4iMNMNfcgyZcoQ9h87ceKEjqoaodPo0aMFlkuXLnXVF2UBFYBdZF/ebVDPHj6I/0z2FFBGfx1E0s1RIny6Yc46dCtRogRhLrtbszOF7MY+KGYPooWUTCSp7TW7vJ7s2aDvMdlTQBx9MRDKOjCH87BmSi1ZsiQxKFSsWDExe+uff/5JIUcc1A0BSdbhw4e7BUlcr1ChgtjBJnGBSHT1nGp8a5igz5nsKSCOARc042FE6xE02bGZAtaR48WDwSM0N01xZ5wC3KEG7dq1q+iv//rrr1nqgaY6ygVG4Xv16iUG7PBfpyY8MsFkz9KUpwOA4G5bC58O5d/ZypUr6YYbbhAkL1SoEMGJBPyxs6hFABtZYN1+Km6i8cLHxBr04TE4Z2/Wq9Uwe7Ex2VPADTVpGDOlsI9YixYtBMkLFChAcAf1xx9/pKA5B00FgQkTJgisFyxYkMpj2odlsns0EZpkIHuQTbO1a9dSy5YtRbrw9TZ06FAtawyPEBoTDLPlatasaYy+XhVlsntECjU6yB6ErF+/Xjg0RHp58uQhuGjGRogs/iOAHWSBu44z4HKa+2BKb0611OB59NVRCOyHyplzmzZtImyPJNMYNGgQHThwQIPcx0cFrGwD/kEPugaBMJPdI8povuNzjP1QMRCzbds2wkaHkuRPPvkkmeaT3COMWgfDvnRww4WtqqIoTPYQrfrdd98R9iWXJO/fvz/t27cvRI3inTRWAcIWs2bNiiQQTPYQzLpr1y7xCU+SvF+/fvTTTz+FoAknaUWgadOmwpmH9VqUzpnsPlrz+eefp5tvvllMtNi6dSvt2bOHOnfunKjJsb/37t27fdSAo/aKwJo1a4RdHnvsMa+PGBcucmRHHxrTSO1H0AMu1oE21OBymyScP/TQQ4TanUUfBPr27SvIji8hUZXIkV1+IpNNZPkb5Eq1zZs3J2pvmT5+69evTzt37oxqWTI2X1j+i6XA2JQyyhI5srstOQzSiNiq2Epyea6bM4MgMdE5LTjehI0mT56ss5o51o3JnmMIT0eAKay9e/d2JDoKU9SmX57Oudln2Ese6/9Pnjxpdkay0D5yZIcXmaBr0KNHj5Ls84HUnTp1Et5hcufOLYiPRSuY6sqiHwIbN24UNsI4StQlcmTHyjQ4/pMHlhxiIowf8u+//xK+jctmOmbZob8OgZcYXIfDQhZ9ERgwYICwE5YNR10iR3Y4mEC/XR5ymqvK2h6unjDLTZIcE2M2bNhwRlm56qqrXN0PnxGQ/4SKwMUXXywqhlCVCCjxyJHdCTc5Qq9ixRpeIpLkmOK6bt26TEmuWrVKhGGXzZmg0eoC/OjDluPHj9dKL7+UiQXZAR6MmpNFK88++yz973//E/HgG3qyF0fPnj0J687ZRZRfxVZNvK1bt6bzzz8/NsuGY0F2TLQB2bPTdx82bBjly5dPPI8FEphplUyOHz8uvJx069YtWTC+FzIC27dvFzbt0qVLyJoEl3zkyO60Cg39dvgEc7rnBvWIESMof/78okBghB/eYryI9BcehwEfL3joGmbw4MHCtnEaQI0c2VGDYyQezgeszv8wcOdFRo0aRfhUhnjw/fWLL77w8lgiTOPGjalevXqJ/3yiJwI1atQQMxr11M4frSJHdvSl5Ug8fjE456VGHzt2rPDUCpJj2iQ8lqQqmFeN5xEXi74IYFss2AmttzhJ5MieqvHwPbx48eLC+FjiuHz58lSjSITHUlUUooMHDyauyROMF6DFAdfPOFq1apV0kE8+x7/qEYDX2HPOOSd2Kw5jS/aJEydSyZIlBTnR9MYquZxKqVKlqH379pmiQT8eYwZoZUhPNxgHAOmDXo2XSbmYXfjxxx+FXz/MjYibxI7s+PZ94YUXCpJjth22TlIhb7zxhojz448/dozO3pXAf7QC8AJgCQ4BNN2Bu9cxnOA08z+l2JAdtWv58uWFobEvmhspsws5BvOqV6+e0uPYNgjjCizBIXD55ZdTrVq1gktQo5QiT/bp06dTpUqVBMmxwymWn6qWHTt2iPjT09M9R43mO2qY7Hz795wIBzwDAbzggTlcc8dRIkv2mTNnUuXKlYVxsRunn8tL5RRa9Ae9CvrsderU8RqcwylAAKsRQXa47I6jRI7s6DtXq1ZNGBVNtnnz5vluV7QcMPXSq6CfjgE7HpzziljOw/3yyy9iCnMqdsp5qnrFEBmyz507V2zZgzc3akz8VyX4du82Wj9//nzxYvH6UpEj88nm1qvSm+M5jQDmPqBsoMUXVzGe7CAZtsqFIbE/15w5c5TaEktjQVCM3jotk23Tpo3YotdLokx0Lyj5E6ZBgwaE5axxFmPJjj543bp1BcnRbPfDsT9qX+snGvwHYaXs3btXpA8HCFkJEz0rhPy7v3TpUmEnOBqJsxhHdoymw0sravIqVaoQnAXmRDC4Zm9So08NcsoJMDJ+9LGt38WHDx8u9MD2TckEcUHfMWPGZHJx7dY9SBYf30sNgR49egj8vS5mSi12c0IbQ/ZFixYRmmIgTVpaGk2bNk0JylgRh5FxKfYaGPdBckyCQTPeOjkG3QYv7ocxeQd6ux0ybf5Vj8Dhw4fFmnXsbx930Z7sixcvFu6dQJSKFSsS9uNSKai9ETcIjRoe59amO8iN2hwtACvRMfMOYeM84KPSDn7FNWnSJGEn1eXGL339jFdbsi9btowaNWokDFW2bFl6+eWXfcMBNW+HDh3EXHXU7F4E4UuUKOElKIcJEQGUIUyPPnLkSIha6JG0dmRfsWIFYfUZas3SpUsLl8x+Q4WaHOmhye5FDh06JBZTYK82Fn0RkL4Anb6i6Ku1f5ppQ3Y4iUD/F6RDjYmlp0GJ7FN7nacu3UTbB/aC0pfT8YYAnJegPKGVyEIUOtlXr14tPMLAKMWKFQvc8QNqc0zCQb8cS06t/XK3AoKvAXhBsOiLAJx9omWIZjzLfwiERvZvvvlGOHAAyUGy0aNHB24T+8g7VqFZP605KbRy5UpRW0R9XzCnvJt0berUqcJOQbYQdccncLJjMwXMTwbJ4ett5MiRoWAk++nWkXc04zHin0zuv/9+KliwILuJTgaSBveaN29ORYsWpf3792ugjR4q+EJ27H0G905WoLds2UJt27YVJIfX1lSWg/oBFWpwK9GRBprwILzTAhWM5uIzHYjevXt3P1TiOBUgABu++uqropx17dpVQYzRiUI52eHuCf69UHPjgP/0du3aiXP4Xx8yZIhx6GHHkLx58yby1LFjR+PyEAeFpRcaWfbYTmdaXSnZ5VxxCbb8xU4qpjoMQC0v82H9xXxrFn0QQPfQah95ntWmHvrkwH9NlJIdy0olyPzrPj2WsQkOm3HjxvnPIkNSUEp2fEZzKshwm4xNG0w8Onfu7JgnDDKamJ+o6gxvsU5lDz7iWf5DQCnZEaXsn0vg8U3adLn99tvPKEhwWMmiHwJY7CLLHX6bNWumn5IhaqSc7MjLjBkzCDuZ4hvnyZMnQ8yeuqTx3Raf3TIyMtRFyjEpRwDzH7Ck1c+1FMqVDihCX8gekO6cDCPACKSAAJM9BbA4KCNgMgK+kh2TVjAgZLpgWq11YMurc0nT822y/pgABc9A0juQyXlRpbtvZMdMJsx5x0CJ6YI8YLEMFr/IFXKYVsur3vSzLF7MsA1sBlvBbjjnZa4+rnqT7p4AtMmkkJ5srHnARBsUIq+r5PSjRDQ1whRolDe7VyFUPDjiLr5Uu3LWmSQKfk0VWYDs+su82efX28Px/2AQwMsYRM9q1WIw2uiZii9khwNHud5bblWsZ/az1gotFJkXe2hZi9iv8//gEYCN3OwUvDZ6pqic7LLGkyvHYACvHmB0hAhr3N36e0x2PSwmW5Je/QfqoXXwWignO8ht9eWG/1ZXzcFnMfspop8HQrs11Zns2cdW5ZOwD2zB/fLkqColO96sAB3bMTVs2FAcGBk1tXllb6VYoZQFzDpwZ73P58EhgJYjyh1LcgSUIoQmL2pxgC8PEN1UQyAPyJOTIJ9u95zC8zX/EGCye8NWGdkxCorBOHtTStaO3tTRKxQI7dQFkS0Yt+a9XrmIvjaylSXHiaKf4+zlUAnZQXB8c8Yb1i6S7Pg1TfDysuYJhQnLddFS4U88+lgT5Q+2QtfRXtnoo2X4mighOwjhVKvL7IEcppFdjvBi/EFuCY18oFtiWl6kHaL8i9odZRBjRNitBz7jQX7ryzrK+feSNyVkR+FPNlCF+6Y1sVBDQG/rYVoevBSAKIWBfUBu2f3COdvstIWVkP10dHzGCDACuiLAZNfVMqwXI6AYASa7YkA5OkZAVwSY7LpahvViBBQjwGRXDChHxwjoigCTXVfLsF6MgGIEmOyKAeXoGAFdEWCy62oZ1osRUIwAk10xoBwdI6ArAkx2XS3DejECihFgsisGlKNjBHRFgMmuq2VYL0ZAMQJMdsWAcnSMgK4I/B+0YOto1BM6NQAAAABJRU5ErkJggg==[/img][br]