Gleichseitiges Dreieck durch Abbildung (A1)
Aufgabe A1:
[b]Der Punkt B(8|–3) ist Eckpunkt des gleichseitigen Dreiecks ABC. [br]Die x-Achse ist die Symmetrieachse des Dreiecks ABC.[br][br]a) Bestimme die Koordinaten der Punkte A und C [u]durch eine Zeichnung[/u] in deinem Heft. ([math]x,y\in\mathbb{R}[/math])[br][/b] (Mit folgendem Applet kannst du die Konstruktion Schritt für Schritt mit >> durchklicken.)[br][br]
[b] [br]b) [/b][b]Bestimme die Koordinaten der Punkte A und C [u]durch Rechnung[/u].[/b][br]
[br] [br][b]c) Welche Abbildung hilft dir, die Koordinaten des Punktes C zu bestimmen?[/b]
Abbildung eines Punktes durch Drehung um den Ursprung
[b]Der Punkt A(x|y) wird um den Drehpunkt Z(0|0) mit dem Drehwinkelmaß α gedreht. [/b]([math]x,y\in\mathbb{R}[/math])[br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMwAAAAnCAYAAABDoaezAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAAAiCSURBVHhe7ZzLyw5fHMDP+9tLLn+AvBZkoeRSSFEuWchGr2Kh2LyUhYRcsqBEVsptoWzkUiJFWLB4JYQosnBZWZL4B/zm833m+/zmnffMmTPznBnP8/7Op05znjMzZ2a+t3OZM8/QnwQTiUS8+CfdRiIRD6LDBODp06dmaGioMB0+fDg9MjLoRIcJwIcPH2Q7NjZm6OF+//7dDA8PSxnbvXv3Sj4y+ESHCcC7d+/M6OioWbFihfzevXu3+fLli+Rv3bplZsyYIfnIJIBBfyQcFy9eZBJFEnkf7t2792fRokVyzrRp0+S8pJXq1vP27dv0yMjfJjpMQDBsNfKRkZG09D8oX7duXfqrgzoYDpO0St06Dh06JNtTp06lR0b6gegwgaBFyLYS/M6TdxgchDJSthXRMuqL9BdxDBOIo0ePmlevXkn+7t271nFLIm/z4MGD9Jcxly9flm3iGGbBggWSVxKnMzdu3Eh/RfqF6DABuH79urlw4YLkky5Ud/BfxuvXr2W7efNm2cL9+/dlu2TJEjN79mzJR/qH6DA9wgzZrl27JJ90t8z+/fsljxMtXrxY8lU4duxYmov0I9FhemTnzp3m58+f0oW6evWqlKkTrV27Vn4r69evl5Tn169f5sePH3IO9SnUs2XLlvRXpC/oDGUidWAGCxEWpWvXrqVHdmDAn509Y6A/PDwsx7KP30wWaNno6Kh18iDy94iLL1tkzpw55uzZs2bDhg1pSWTQiA7TEoxpIHaxBps4hmkJHKXfnYVJChaLXrp0KS1pBxanct225MN4URfGMk6sQuMOw0reUMaiq4JPnz6dltQHQdFFoi4EGDHd90hr1qyRrYuvX7/KJAUy7BWdXt+0aZNss4TUufLx40fZsjBW33/52oO3wyAg9UrfByBybNy40SxcuNCcO3cuLe0PENSVK1fM48ePzdKlSytHmkHCR3cYJrCItOz9D91LXrbCo0ePZNsLDx8+FONtq4V59uyZbE+cOCFb8LYHxjA+MLvD4ZrK1jgx68MSkeySj14ZGxvzunZVmI2iXuqfjPjoTmf8ymSgx+VnAOtSptMmdK62WTQD6bIHL4fRm84m2+JCRRcOlgm/Kk0IT1Ehsr5rMuGrO56/bO0aq6pDy18dsMh4m9A59WGjLorswcthdFGheh6JCm3ogsKi/b3QpMNo3TzjZMJXd5SXtRq8H3JF5jpwLy6Zh9a51lcWGIvsoXQMQ3+VwWByw2bWrFlpaTFnzpyR7Z49e2RbBPUyyKJPzTbbZ2Q9le7T6dgyOJ+36Jwzffr0CZ8F02/XPjyJfn0W1n/RL2dNWH7foOKrO2THs7vGENSVGJmMcVwfxFGXzrahh6z+sjrS5USfP382+/btk3xV6uj827dvXuO0QntIHccKkYSIolEFL+cUUlELose7IJJpPfn69HsQTXi6UhRtOIdrZs8j5SOmRluSLUrqtym+H341Ac8WYnxQR3cudBzkGpPa9KDXJ+kKBlJeh0U0rXMXNntwtjAsP2ed1MGDB70+s2WmheNZaevizp07Jnkw+QZeYaYET161apVEgEQgUu6z8vf58+cSHROBdL+lB66TRZ+hKErOnz9ftrdv35ZtGTrlaVsfVpfEmCX6agSuS1XdlaGfGuQ/Q8iS1UNizFLGPbx48cJs3bpVynTfsmXLZH9dQunchdUeUseZgI5FNEJAWZTS/b7RA7JRh2u5ol9RtMmiEw4k6s6i13JFST3XB72fOhHbhQ6uEyWnJdWoozsXdZ6Te9frcR/Ze6lCGzp3ofUqhS1MchOyLYpQL1++THO9kV3RSz9UV/zWZfny5WnOdP+IAujv8jtRujNK9gOsNUsMRPrPtF5VX6y2pTsXK1euTHOdVubJkydBWjobberc6jB0NWiCk6hgduzYkZaOByGEIPsgOE+vQp07d26a66Av5G7evClbDDE0dCezg8sQ6cCBA9269ctMH9rUnYt58+alufFv1JugTZ1bHUbfgCLYmTNnTlBiSKZOnZrmOm+ke4XZDxSk/P79WyI00Zp+bBOKI4IlrXXQpEqm7iLDt9Gm7lxMmTIlzY2P+k3Qps4nOAzTgEQ1mxGEjs44SHZwy3VDwHSg8v79e/neHo4fPy7bfodpdQwcZfMfAL6tbpu6K2NkZCTNddCo3xRt6Xycw+CVR44ckXwvAuYLwjK4FkKlG0b3QQkhWNauKawNItKcPHmy1PCqjhWagH73tm3bxFnOnz+flpYTSncufOVDEKSFw3EVXb/VFHV17sL6vEn06ZIIWmYEmLu2ofs1JU1tuqdD2WwKMxV6HrMozGAwc6Jz/CTK2c++/MyGz4wJ6HGaiu4nT53ZoNDwbHXew/SquzL0vCKYBWN2T99doDvNk1TXyLbK8zWtcxc2e+hKgIfQi9mEnjdsku3BERz7bGSvwXHqENlyTbYH9hUe96r1cB1f41Cj+psvLusQSncu9Hx0kAf52urOl5PQB/fjS9M6d2GzB7FsnffPpvziNBSRP4aUbwVoISinzjwacWytBw7CPh6WOmxC9RUeUA/HVjF+fcYQwm6LkLpzoU6Zrxuoh33IPO+IanQknK7KNaFpnbuw2UNxG1sTjSohmsQ8vsJTI0JBvmjdOGvEDoEOo6zSQvRKkzp3UWQPwR0GiEJczNbK9IKP8IhgKJXoUEWxHM95g9S6tI0apa2VaYomde6iyB4acRjQC1Ztgl3YhKfdAZTJfq5Z9bqubmRkPBoMq46B6tKUzl247KExhwEuzIPwsCE83yY8HRdpqiI46qPrGFLY/wd0PIN+m26RQ+vchY89FK4lCwHvEfhj7jdv3nRfJIUm+84n6b/K9x8+b3Z5abp9+3azevVq8+nTp0aXbkw2WCWcOIrkkXnb1NW5C197iP9LFol4Y8y/ClikniSImOgAAAAASUVORK5CYII=[/img][br][br][b]Gesucht ist die Abbildungsgleichung[/b], d.h. ein Ausdruck für x' bzw. y', in den man die Koordinaten x bzw. y und den Drehwinkel α einsetzen kann.[br][br]Die Zeichnung und die folgenden Schritte helfen dir, die Abbildungsgleichung herzuleiten.[br][br][list][*]Die Zeichnung zeigt die Drehung von A auf A'.[/*][*]Die Zeichnung ist ergänzt durch 2 rechtwinklige Dreiecke ZQA und ZPA'.[/*][*]Die Katheten der Dreiecke sind entsprechend der Punktkoordinaten beschriftet.[/*][*]Die Hypotenusen der Dreiecke sind gleich lang (z LE).[/*][/list]
Schritt 1:
Betrachte das Dreieck ZQA. [br][list][*]Stelle eine Gleichung für [math]cos\;\varphi[/math] und eine Gleichung für [math]sin\;\varphi[/math] auf.[/*][*]Lösen anschließend nach x bzw. y auf.[/*][/list]
Schritt 2:
Betrachte das Dreieck ZPA'. [br][br][list][*]Stelle eine Gleichung für [math]cos\;(\varphi + \alpha)[/math] und eine Gleichung für [math]sin\;(\varphi+ \alpha)[/math] auf.[/*][*]Löse anschließend nach x' bzw. y' auf.[/*][*]Wende die Additionstheoreme auf [math]cos\;(\varphi + \alpha)[/math] bzw. [math]sin\;(\varphi+ \alpha)[/math] an.[/*][*]Multipliziere aus.[/*][/list]
Schritt 3:
Die Terme [math]z\cdot cos\, \varphi[/math] bzw. [math]z\cdot sin\, \varphi[/math] kommen in den Ergebnissen beider Schritte vor.[br]Setze die Ergebnisse aus Schritt 1 in die Ergebnisse aus Schritt 2 ein.
Musteraufgabe:
[b]Der Punkt A(6|2) wird um Z(0|0) mit dem Drehwinkelmaß α=36° auf den Punkt A' gedreht.[br][br]Berechne die Koordinaten des Punktes A'.[br][/b][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAATMAAADPCAYAAACZfzaIAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAAEe8SURBVHhe7Z0JvIzlF8cPImv2XQktlCzZUtpDxU0hKiX/ZKm0KUqUkooULShb2YmEFJI20T//0iIVsofKWsjuPv/n+7zvy9wx996Ze2fmztx5vp/P+5mZd5l531l+c855zjlPjkWLFimxWCwJT3Jyshw7dkz+/fdfady4sbs2jtAnr4JdPv/884Dr01pCPebDDz9U+o00t4G2p7ZE49yi8Ros2emYRL9+llCPyarzOnLkiPrnn3/UmjVrUqyPlyVnjhw5JNhFKRVwfVpLKMfMnTtXmjVrJocPHza3PA60X6Al0ufGEo3XYMlOxyT69bOEekxWnxcEWh/rS0hiFskF4UpKSpIPPvhAvvjiC3PL41AEzS52sUviLjmNDGcx2qWU5s2bGwHDIgNuecx6tlssFktaZLmYBRIyDytoFoslWLJUzBAoz7X0FzIPT9DYzwqaxWJJjSwVs2+++UbmzJmTqpB5sJ392N9isVgCkaVi9vTTT6crZB7sx/4Wi8USiJgYALBYLJbMEjdi9v7775vh165du8qBAwfctSmZNGmS2Wfw4MEmh8ZiscQXP//8s3svdOJGzOrWrStXXHGFfP3117Jp0yZ37QkOHTokX375pZQtW1Yuv/xyI2oWiyUyMCgXroVcUhLl4d1335V//vnH3A+VHJQ0uPdjBkRLn5f7yIG6sbFjx8r48eOld+/eJ9WObdiwQfr27SvVqlWThx56SPLmzetusVgswYA3g6js3btXWrVq5a4NzMiRI917madevXpSu3Zt+eijj+S9996TSy+9VG6//XZ3a/Dk0BcQtJiRmY/VEwoZOQarKtBpLVmyRK677jrzRg8dOlQKFCjgbhHp2bOnDBo0SEaPHi0dO3Z016ZNqOcWrevPTsck+vVDqMdk1XlhMOzfv1+2bdsmlStXdtcGJlxiVqRIEWnTpo2xxvr06SOlSiXJ5s0zzO+5SpUq7l5BgpgFC1ZcqGTkmNROa9euXeqmm25S2vpSK1ascNcqtW/fPnXttdeqmjVrqpUrV7pr0yfUc4vW9WenYxL9+iHUY7LqvCjW1laZWrt2rbsmekycOFE9+OAzasQIpXr2HK6GDBnibgmeuBrNRMUbNWokv/76q4mdeeg3X7S4mX+ZM888011rsVjiAX6/ixYtknLlksxjbv1/48EQV2KG+4lgEeRfvHix6bsEn3zyiTZNN8vVV18tp556qllnsVjiAxLiixSppZfa5nG+fBWkdOnGZnAgFOIuz6xq1arStGlTWbp0qQn642t/9dVXUqtWLTPiabFYYp+tW7eaFCuMEqywsmUdq8yjbNnmsnv3wZAELeJill4gMVQI+nuuJm/EmjVrzMBAjRo1tJqXdveyWCyxxsaNG2XatGnyzDPPmKVLly4mM2H79qOSP38Fdy+HXLnyanezubHaduzY4a5Nm4iL2emnn+7eCx+IWc2aNeX77783IzL79u2T+vXr6zcgl7uHJVYI959ZajRs2NC9F1kIcVhEli1blu6ycuXK46GgiRMnyvPPPy+bN+/VItVCGjQYon+3OeXYsTyybdt6eeedJvLHH0vMvh4lS16hjZdKRtCCIexitmvXLhkwYIBxB4lxXXPNNbJw4UIz7BsuCPITO5s/f77JO+M1Klas6G61RJJQf8zlypVz7wVP/vz53XvBkydPHvdeZInEn3M8Eki8/Jdjx44ZT+qHH34wCe3nn99KChbsKErVktWrv5BNm1ZIiRLd5JxzPpVTTikjc+d219bbIvcVHBgMYCAATyw9wipmf/31l9x1110m8a1Xr16yYMECfaLnSMuWLYNW12AgyE+wH7P1xx9/NJZawYIF3a2WSMKIsv42ijz3HCMyIuXLiyxf7m49mVy7d4tcdJGz71tvuWv9YNSqgnYzPvnEPMyXL5+5DRqel+fndXxdEm+9tt4zjN9zG9HkfBk1d8/XcjIlS5Y0Rgd5a++8847Uq3eX5M3bxN0q8u23w6VQoepSrFgL87h8+fH6u3WuFr7R5rHHaaedr/epH1TsLKxixgv++eefMm7cOLnzzjtNlv6QIUPkP//5j8yaNeu4yRkOvPImW74UXcyfxh9/iP5AMaFEtm9nOMoRuIywbZtI794irVuL/iDNqr///tvcxiJHjhzhyydyxx0iffsSyXa3JBY0TE1rueqqq4xVhlVVpEgZ7Zk1cI8ULVgj9Gf8h/7tPuWucShSpIP+Ovyq3c+N7hoHBgOIjWPdpUXYxIxRRdw+hIuSIg+sqFdffVXefvvtFBn74YKRTVxaS3QwqS/ff89fq0ibNqJ9B0fYELhQQQCxfFauFG3Si/Y1zGrck1jF1BBynh06oLoib7whcvSouzVxIHyQ1lK4cGGzH4XjBQumDAF9//14bW1doz/n3drAWXZ8ESmsrfIi2tsaIbt2/e/4sn//Ri1o1xvvzvyZpELYxAyL7LfffjPCgpt52WWXaRPxNFOq8N1335HS7+4ZHlD8zz//3MTLIiGSlsDk4oerP1/JnVuE+jn9D2yEbVHKWIeHwmX0ylL8y1PWrRP9Lydyyy0i553nrhTz3QkJ3+cPId7Gjy5d/J6bhgYGBjZuvdUR4zTc7ESHZPZixU58tkuW9NWCdEiL1EJZu7bLScv+/btlz55ftYU2NcWyZ88X+j/jaJrhqkwXmhcrVkzOPvtsE+Rr0qSJ1KlTx4wq0qqH+MKoUaPkp59+Mu15KCZdp7/AO3fudI8+AUXkLB4IlT+ocm79IyJH5bXXXjNfLIZ2S5Qo4e5hiRSkvTAymQcr6rrrRBhwmT2bSLDIDTeIJCWJjBsne5KTzZ8aI8xnnXWWCQPkfOIJkalTRebNkwNnnmk+x9MKFRJ5/nmRgQNFm/Ry8MILtce6XUoUKSL5XnpJpF8/RyinTJGd+vtETuEZZ5whJfLmlRydOzvP99RTovr0kRzaBTHnpEUxWT8nr80fXC59PkKdrv4uHWvUSHJo7yEnwsl36+OP5UD9+voHtNZ8H7E4+R4XZ6CqRQvRK0XmzsUUS/Hcf2gLlEEuri2fvk5vG9exe+9ec+2ptaiKdTA4gi00D5Zhw4bp3+w5+l5wkwr/888wrSNOtkLImKKmIEmr/mvx4sWIomrWrJnSH7i7Vin9RVGtW7dWHTp0MDWUwZDaafXr189sYylUqJDSAqmSk5PNtrTOLTVCPSYarwGxfIwaNowPSKn+/ZV+8/mAlbrqKqU/EKWWLHF3OgETy6oxY5S65BJnX48tW5SqW1epxo2V2r3bXeny11/Oc/I6L7zgvA5wO3q0s57t7AfbtyvVoIFS48c7jz14Xfb1vc5XXnHW9eqljh096q70gX1z51aqUyelDh066bmZIPc4e/Yo1aKFUuecwwZ35cmE+j5n1ecfidrMjz/+WL388ghTcxnM0qNHjxT6EQphT81glLFMmTLuI8dyYzISrDP+1TIDLizPd8EFF5g4HC6sDfxHEW2RyIwZIlhV2r03o3z689Afuui/c2ebX/yIf3kTD1u82NnXw4u7EUx34yvHKVXKWF1StKjI6687+wK3rMc9HDTI2Q+wzBlhJCifHlde6RyvrbOcXI8vnPv77zv3W7Yk3+Ok596zZ4+5NfA+aOtOVq8+cY6WFGDtrlq1TA4eTH9Eed++iWYU1Fc/QiFsYqYtJXPipbwvmAt+Lm4nt5kN7N58883GJVi+fLkZaDjFDRhbosT//ifCiBK95Aj8ezRv7ggEw+cbU45E4XYFBIEABov8/pCMm3bJJSIPPeSMFiJcNOTs1ct5jAta26nj8wgUugiIdg/liiscIcVF9oWRVWJ/uDg1argrU5JCzMBzhzjOT8izM7QASm/hsyf/k5HNn3+erF15/ceWCvnz/6pF70vzu84oYRMz4lbly5eX9evXaxteG/IuWE7EMIrqf1kEzxKn8EP9+GMCl8wuQ46Gu0Fz7rki117rWCgffeSudAgYP9q/3wn+M4hQqZK78gTkK5oRw65dnbgZFh9xrAULRNq3F2nb9iQBJNAcFAwQEN/jOrgeXwEikP/jj45YB5scTL4ZibTEEvX33HICxIw8s7b68yLr4KuvHtWGzef6Ld8iyclH9EewR3+M6MVMWbp0uOlnlpn4d9jEjAAxHSLJNaOMwYOgLiMQ1E4WL17cXWuJO7C4sLzOOed4PthxSNfwOv8iPP7umz+I2dq1jjUX4DvByLjBczcRzh9+cF67Z8+UQpoR6tVzngtrCmsMEDUC/nQoxtIMNnyBIOOOkhzstn5OBPxTMQItVP2QH4agkTj/8MMPy44dS7WV9rz2yrvp/44e+v9vuH62bTJw4MDMV1c4obPgSC/I+Msvv6gGDRqoevXqqbFjx6rZs2er5s2bm3VsC5YQT8sQjaBpNF4DYvIYL/Cf3kLwfN4896BUXsMLqlesyJfGXXmCFMcQDL7sMue5fYP+fgR8nUADAEBgnwC/77muW6dUtWqBByR8OOl10rkWCOl91oS6P4TjmGg1Zzx69KjasGGD2rFjh7smPIR1AIBk2enTp5vyIvrx4/8S0JswYUKKRFpLnIH7ROkOVsgFFzhB70ALLiPum/4OiJuPZZJsQ4T0GwPW0siRJ3LYPv1U5M03Mx+bwpIiwA+eq0n8jPo/XGhKtiwRgxg6sbRwe2phH83EVGSqN/KCCMq+9dZbZmDAEscQS+JHz8gjorZ0aeBl4kRnhG/+fJFVq8yhXiZ4KBwfzVqyROSVV5zBBp6TWx6zPrMQ4Cd4j0AyuEA8TrtGZrQzFHCpqQfVf9qBXGZL9Ai7mPkTy3V2liDAaiEORoqFtlpUWj9YBILYGSOObr2mKUz3hyA8GfXE4byYlQ9GzFjPqCVWIXGypk2dWx6zPsBxIUGAn3NlnkZGaL/5xhnlZLQzFKg35r0hjQSLz5JlRFzM6GphiWO8dAUsLm21HEnLxSMwT84ZuPWalLSdBGLm9TkLMAdqfkQBdxKrqV07pwgdcA3JTA+Hu0mAn0A/Af8BAxxRY5QzhHIoA8LNe0R9cGYHJiyZIuJiZolzEDJysmiBc9556ZfqYEExUujWa6Y6fyl5ZMTGsIj8RYmWPbiTlEw98sgJgUEsevRw3EG2Z6a1D1APynUx+k68j1HOUPH+rKkntXmPWYoVM0vqkELhFfbeeKMJjJuM/rRAgBA0mD5dcvIcgfBiVogeaQ0eVIk8+6yzDiHzTc4FkmUff9zZzn5uVUlGBhoU8TwC/kC6SaipAYRQqPNkcKtOHXdlfENe6PEBmDgjbmY0t0QXkhcpLPdtlEg/OpKiU8u2p6icUSpfYSHHyLe5ACNZPG+Z0qUlJ+7dM8+YEqJjjRubAm4GDHy7xvKaHM+2QOdEYTTbTaKtC+fAQJRvofkhbYFRVE7eIzDBLLlQOSmXwtpzz2GTdntZ0oLkcBoPnkJFBMnCnTqJ0teyTZ8jiaKx3MIoPWgCcPDgQbnwwgvN+xNXuCkaQRGt/JcQT8sQjXOL1vVnp2P0j9u9FwCKsynS7tJFqYMH3ZWkeaWe55UaAc8rtTwzD69IvmFDpbZtc1emzRKvmJ4C+u7dlSpXTqkff3TWpUKo71lWfZY0bdB/DqY5xLYg349YwrqZloiyZcsW914AGASgFg9X1k3lgIgOGmE1sZAHN2WKM5JJX7Igy2iO50Z5FREU0fv0YotncDGxnLGssdCwhuMJK2aJStu2UnnECPdBGlAH+dhj7oMww4giYsBIIE0O3YGAiDbbpH6UtBAGJrp1E7n4Yme0NMjyJVM7yHnSe4/zpLdaNgr8I2i4+XwGhAhw36mtjgesmCUiCNS0aXI6lklaQuXuJy++GDlB8+ovSeVwk2EzEswPGpJbySUjyM2gxqhRwReVa8zoLEnEvC9088hsPWGMgZjRjYYZssgRxFJj0Ic4IvFSukgTowxlmTFjRsD1aS2hHsN5WTFLRF54wRmBg9SEyhMyoJsqx0QKRhI3bDhewM58EmEBq4+omW9hPJbVwoVOUfjMmTTccjcEh3G9LrzQcYu9nLpshidoDLSQJ0jHG9xrShOZ0IY2X6EsdMsJtD6tJdRj2N+KWSJCrGrOHNlPGgX4C5q/kBEbyhm9r0q0RgO9kc1Q2JbZyoM4AUHLqT9z0jRwOxE2rDXucxvKEo1jEF8rZolKlSqyws9C264tmcM33ZSlQhZNfvnlF/de8MRL/CgcIGieqHmL/+NglmgdY8UsgTlAHhEjia6glXz7bclD7AqyuZBZsh/2m5roaAtt3n33yQGfEbnt1GFaIbPEGfbbmuDgahV6/nnJ51MfWZKSpUcfdR9ZLPGBFbMERiklB1u0kEZ0ftCsKF5c/qSVDQwZ4owGWixxghWzBKZIly5yIRPoapaVKiW9GzaUP8m7IokVmG3c68hqscQ4ttA8QSn30ENyNpOEaL7W1liPatXk0ssvN7Po5NOWWvXHH5f8bsH137Vry/KXXxZlY2iWWMYp0QyOaBXAhnhahmicW7SuP9LHHLzhBqcAWy/fliqlbmjeXPXp08fd6kIReNWqx/czs4+vX5+w75lHNI5J9OuHUI9hf/tXm4CMqFRJNhcsaCyyfvXrS978+eUO/9nAqV9kRBOXkzSNvn1N2+rTgp2f0mKJMlbMEgxmz1q4bp30a9DAuJYqRw5p3769nEN3WH88QWOhxXTv3lKO+8wJYLHEGFbMEoiff/7ZTPsHf2prLFnfXnnlldLM67YaCATNi5XVrCnrunQRoSnhG2846yyWGMGKWYJAveMbfgJE4TBWWSgcJnVj4ECnpTZtq9ObE8BiiRJWzBKEESNGnNQOukmTJhmfiJX+/LS/eeIJZ4YiiyWLsWKWAHz22Wcyn0l0fWjdurWc7z9ZSKh06ODMNdm7tzPDkcWShVgxy+bQKdTfvaxRo0bI7mWqtGghcuedIn36ONPGWSxZhBWzbA5Cxmw7HvSlCpuQeWCdMf0bsbTMzmVpsWQQK2bZmGnTpsl3333nPnJINQ0js9StK9Kvn8jo0SIffeSutFiihxWzbMqKFStk4sSJ7iOHdNMwMguzFCFo06efmDzYYokSVsyyIUwT5h8nq1ChQvjdy0BUqiTy9NMic+c6k5RYLFHCFppnQ2bOnCnf+AXj27Vrl/nRyxDIs2uXVBw/XnbXqSM7Lr3UXWuxRBC3TjMoolEwCiGeliEa5xat68/MMZ988olKSkpKsYwbN85s8yfi5/bnn2rLjTcq9d577orgiPZ7FgrROCbRrx9CPYb9rZuZjfjjjz8im4YRKqVLy0Zee8ECkfffd1daLJHBilk24s0335RDhw65jyKUhhEih4sVc3LQGBDwS9y1WMKJFbNswqeffirff/+9+8iBtj4RScMIlfLlnSoBZlD/7DN3pcUSXqyYZQOWL18uC5ml2wfSMJrTtidWOPNMp44TN3jpUnelxRI+Ii5m1atXd+9ZIgFuJe6lL+W1JXQnJUaxxrnnivTqJTJgAP2I3JUWS3iIuJhluCuDJShGjhwpmzdvdh85ECcrRqwqFqldW6R7d6f06fff3ZUWS+aJqJh9++232rs4U5YsWeKusYSTTz75RD7++GP3kUOrVq2kYcOG7qMYhbyztm1FXnxRhDk6LZYwEDExo1tD//79ZePGje4aSzjZsmVLwDSMmHQvA0FZVYMGIoMGuSsslswRETE7evSojBo1yjQDLFu2rLvWEk5otnj48GH3kUiePHmyPA0jZG6/XaRECZHXXnNXWCwZJ+xippQy3Roopxk8eLCUKlXK3WIJF1OnTpUf3DkvPZjvMibSMELlgQdEtm/notwVFkvGCLuYrVy50lhl3bt3t1ZZBPjxxx9l8uTJ7iMH0jBiPk6WFgwIfPqpiK3HtWSCsBSaFypUSKpUqSLJycnSpUsXueSSS/Qf7gOyevVqadu2rQwbNkzq1asn69evlz///NM9KiVjx441i4c+L/eexYM0DN7LHTt2uGvw0kpIp06dzGcQz+TfuFEqjxwpa7t2lQPMLWCxhIpTphkcaRV/HjlyRA0YMEDde++9at++fWadttJUzZo11eLFi83jYAnxtAyhFqZCqMdE4zUgtWNeffXVk4rIv/rqK7Mtq88tNULa/+OPlf4CqUXz57srgidWrx8i+p65JPox7B82N5NymlmzZkm3bt2kQIEC7lpLuCDD3z/LPy7SMELhmmtEm/BS4b333BUWS/CERcwOHDgg7+kv4Ndffy3nnXee5MiRwyxVq1Y1MZ5GjRpJrVq1ZNWqVe4RllAgKTau0zBCoUMHyXHkiFPHabGEQFjEjLSArl27minNfBfaNp999tkyfPhwGTp0qJQrV849whIKpGHQPdYjb9688ZeGEQJbWrZ02gbZGk5LCIRFzHLlymUsLzrE+i5169aV/PnzGysC6yzeg9RZwRRtoWDd+oKQxWUaRpAc5Xty330iw4aJ7NzprrVY0ibsqRmW8EEuGWLmC38SMdUNI1Iw29P114s2690VFkvaWDGLUf7999+T4mR0w/jPf/7jPkoAbrmFcW3mzHNXWCypE1ExO/fcc411Qd6ZJTRGjx5t2mD7QrPFokWLuo8ShK5dnVmefvrJXWGxBCbiltnff//t3rMEC91G6IjhC2kYF198sfsogaAcrksXeh05VprFkgoRFzP/4LUlbSjOnz17tvvI4YILLsieaRjBcvnlIlWrOoJmsaSCjZnFGDRbPHbsmPvIScPo0KGD+yiB6dRJ5LvvRL7+2l1hsaTETgIcQ5DhTyWFL4xcJqR7GYBCK1dK2TlzZM2DD0pynjzuWovFxS1tCopo1FhBiKdliMa5RfI1li1bdrzeUouXuX355ZfdrekTjeuHLH/PRoxQatgw98EJYvX6IdRjstO1QDSOYX/rZsYAe/fuDTgpyV133eU+shyH94Q47P/+566wWBysmMUAY8aMOak1EmkYRYoUcR9ZjnPKKSLk2vm0i7JYwIpZFrNgwYKT4mSXXXaZjZOlxUUXOdPWjR/vrrBYrJhlKRs2bDgpy580jGuvvdZ9ZEkVUlXmzhX57Td3hSXRsWKWhdBe3D8NI6HKlTIDLjidQyZMcFdYEh0rZlkE7ZF+8ivRIU521llnuY8s6UIh+tGjIn5zh1oSEytmWQDlSsxg5Qu5dUlJSe4jS9C0aycyebLkQNQsCY0Vsyjzzz//mGaLvtC0smPHju4jS0icf75pF1Tar6W4JfGwYhZl3nrrLTPbuy/UXRYuXNh9ZAmZW2+V4l99JfL77+6KyEEr+FC5nNrSEMjIdyHU1wByGUMlljvgWDGLIvPnzzftxH1p2bJl9pqUJCsoVky2XXWVyDvvuCsiR+nSpd17keN8rM0okJH47Cnk+cUoVsyixLp1607K8icNwxaRh4ftV1zhpGmEuUsLxXXk595wgzEAZc0ad0MQHD4sMmiQSL9+IgcPuitd2MY0B3QHv/FG5/npdPThhyLJybndvdKH5+X5772XdlvuyiDgutauFXnxRacHJq9/000ijz7qTL3g321pzx5n26hRIj4D8DGFLTSPEqRhMAmyB5PAMHlvRkx9S2CKLlsmRX74QdaHIf5I9QWT8fz7b3556ikRIgPJyY7wtG+vZOfOHVo7f0sx0Qww5wUWD000SYObNEnM8WeccUB27dolJUuWlKNH88jgwU5FVk5tTpQo4RzL3M68Rv36ziTvIvu14Kw1x/nDvBvMA1GoUEktmDmEApLnn+f59pjJt+lU7E++fPnMNRUpUlTmzTshTPqU9fk6wuhNuYCh27kzz3dQdu/eLcWLF5fly/PISy+JPPww56hk+/btWtzXnPQeZBlunWZQRKNgFEI8LUM0zi2jrzF+/PjjReTe8v7777t7nEw0rgWicUzUz+uRR5QKctLpYF6Hp9Ifl+rfX6lOnZTq2lWpbdvcjWmwebNSd92l1GuvKXX48DF3rVJHjyo1cqTznI8/rtT27e4GzaZNSnXr5mx79113ZTocOKDUM88odc89Su3e7a5Mh5UrlbrlFqVat1bqs8+USk521nO7fLlSd97pnIP/V/TQIaVefFGpBx5QascOd2UQROM7wP7WzYwwv/76q0yfPt195GDTMCJIq1YiM2a4DzIHruCiRY711KQJYQGRLVuYaMbdIRX4Oyb1bf9+keuuE225nPAxMc6pXitTxrFwPKsMTj/dsYbobrRuncihQ+6GMENLOAy3Zs2cvpc5cjjrueUaaR3HNTOmwjV4cF4Up/AecA3+rmhWY8UsgmCef/DBB+4jB9Iw7r77bveRJewwmILf5DfQkhE2bRLtWjHqR7DcmTCKH/kXX6T8kfvDj50oSY0auJdOVxQP7QkbIbn6aqcjuD+IybvvivToIXLqqe7KMIJA/vOP8xZxfp6Q+cL0tgULOvsh6L5UqeI0/UXMcItjCStmEeTtt982guYLAf/TTjvNfWSJCESyZ850H2QcxhIQnnr1nOqp884TqVRJZOVKJ3ieGgTQCXM1aOBYM/v27TPrERLGKFhXvbpZFRDtNbn3wg8C+cADIlOnitSqleyuTQkhsNTCYHnzJgdtoUYbK2YRYu7cuScNYpCGcREdHyyRpU4dR338upGEAlbJ4sWO8CBmWDCkf9Wq5VgrfLSBRvWw2L79VvQfliN8cMj1FwmwM5DANgLuCMLAgSI33+wMLDCy+eWXDAIEMJciwMaNG917J0BHcS8PHBCpVk3Ef97uo0ePGiHmfaGLeazE/sGKWQRghMc/y9+mYUSZFi1E/CaGCYVffnHiW7hUnigBOaMFCjjuot9MgAZcL0QKsSpWzFnnjfYhFAgg1hGxuIcecoSPuBn7k/NLKsfrr6ftxoYLJs/xh/MhPYRrJE6YK5e7weWwVvKSJZ1rwzr1czyyFCtmEYA5L31dhVP1t9d2jY0yWGf8IlGNEEFw+FGTJoGrSHzJgxgYsSbcSNxJfxAz8r3Irc2b11nnfRfI1cLjROxw8xgcoCUbXaDeestJrUAoMCgRlAh6mwHBbXz1VcfaouT1nHPcDT4gzFiWZcs678H27e6GGMCKWZgZr7+dv/C37gPlSlWInFqiCyPGfgMwwYDFheWF9VG7trvSBfeKgQDADcUd9QWhguLFTwTwcc2A5HkvgR4L7/bbyf1yHuPG4r7dc4/zGrh6iF8kYTAKEE3c2wEDHLG94w5HaAMNDtCyivW5czvuNu5orGDFLIx8/fXX8i5DUT7UqlXLzLBkyQIY2cTMwMwKAS+Az0JmPdnxvgtuIOCG+v1vBSQZE0+DhedZazQSRrT84T8P6wyLh9ePJGeeeaaxQvHGSeIltMdAe8uWJ7uXHlwLIo1YQyBXO6uwYhYmdu7cabL8feGfzwpZFkMyFan4QUKs6vvv9Q9D/zJInSAtI9DCYAAaxUCAf/qCP56biXh5NeSeReYP6wOlbESCI0dyG2HGxUWgevVy3q5AFplHjrQ2ZjFWzMLE2LFjZfvq1SkionSNpbzFkoVccw3DdkEXVRLUJvUCwSIYTzwr0NKzpyNO5KEFiKOnwLPMEAyvTt1zR/3Bbdu2zRHT1KyjcEDKycsvO/E5rpV4HWVU6WkVZVRYcF7ZE7GzWMGKWRggMfYL8ppIIlq1yvgfpGE0IHpsyXpIW58/332QOrhcnqXl5Zb5s8VVIS95FFEgduYF6xEGwE30iss9ywxx4iuBUP33v2LiU/7gtuK6MdDgWx0QTrA+hwwR+eYbJ8j/zDMilSu7G9OBrhm8T1w3Yp6ahZkV2ELzTPL777/rf+o3zGzbOfSXNof+26quP/BHLrpI1nfuLIci9Y20BE0u/eut9txzsvKJJ+QoI5x++BeVI0R9+zIB1GHTHMB/GsDK+pdPg4CZM3PKuHGOgNG5onjxZNm8Oaf06eO4k/37I1x7TUF6Tq1gvIZSBYwVtGIF33MnRsXoIHrHOqwlRkOpAGjYkOfbbM7Bn1ALzdmf8y5TpozW9ZwyciQxMzHnmtZXlID/H1pdmXyH4nkGsvbsyWuOA64xd+7d5hoPZPVogP7XCJpQiz8hI8eEeFqGaJyb//7afVA9e/ZUSRUrqqRSpVRSyZKqdbVqam3p0krpx+qcc9TaLl2U2r/fPSI4ovU+Z8V7FgwROWboUKWmTXMfOPgfs2CBU2DdvbtSe/a4K/3wPeb3308UZXMs/PuvUr17K9WmjVKrVjnrfvnlF+eOy5YtJwrKb7zRKWDv0MF53KKFUmPGOAXpwRBqofmuXUrde6/zWuktgZ7zyJEjasUKpVq1UmrAAIro3Q1pEI3vAPtbNzMTkIbxKxXF+BNocKlScmevXlKZ4SAe67/YChSZ8xdML7O0amAskaVxY5E0WmvzEeL6ASON/pnvgSBeREUAePWahEhJ58BIIeIABSl09IGMCPqIMbkUwX6sKqyxmjVFnn7ameM4UvGyrVudKoSMgoXH4LDnipOiEStYMcsgX331lcxgmjO+HQhXvnxyeatW0pyA85NPOhPV6vU5CP4SgH7tNadNAn4MQRZLdCE4ROIYLSMCQMoEH8377zuNN4IBwSGLn2Nwt7yxHuJivBQpHghcoFpcYk2tW4tQKMLxhFyffdYRx0OHTnTZCDc0sSV7iNdMbxk+/OS44Z49OUxyLa41NZqxhBWzDEBTOrL85eefHSHTS7n69aUz2YYeBD0qVhRFtBdBI2mIqeX4JvC3TJ8VZmiKpXqQ7A6tKjJRrxks/NAxxrHMaOUT6oj2j2HulpsaTK4TKl6ZF//Z5MPFElbMMsC4ceNkBynarpDRiOou7RsU8g0u0zNG//UeoEkVY/IIGr4H7UUBW3/iRGdmbiK3lshz5ZVOLgW5DxGE9Aa8WgwyOhHlzBmaL3bQGwaNMD+E2PYC15JxOf0fbcQ61oi4mDGCkp14X9vfi957zwlyIFDaDm+pLbL6/nUvcNNNcoR4Ce0HuGV/xI92Ax6M75O0ZIkoJh6GX8ivMI2Rci9ullmwznBX8WpDmTcgluF/gK9umzYnKgBiiYiL2elYJtkEugyMJsiB74Ao6R9H9aZNpUPbtu4efhQqJDsuvdS5j6WGXc5xlNjwzSCDEnc0hme8yQ5QAPDCC069oxEzovUBSLFfGKCPPj3QiFFFydiKGOTE8R9OJ41Y7WIVVjFT+of6nZbu2267zUyAQOCzjZZx1rEtniHfhh5lJhmIa9HLqWefLZ2oFk6D3Qz5eD1k+LsmuYfjSaPGUou1wEM2Y8kSZyAZKKT+ape2hPnz4HP0gY/W24+E0nBYUwwq9O7tLF5NZrjxBi4CBevDCY4F0RBCvZEaac0sYRWzRYsWmcx3IG1hypQp5j7r2BbPcD3bSJlGhBCjUqWkQ+fOUolU7fSg86kH3zjEjcADY/KkX1siBt0pMH49jKBVvNVpE+HiK2SENxEHDOlw4d9tOBL8TdgjCmyLcLwxM4RNzMg4pj6xibZDKbhu1qyZWRj1Y7ZltgWa/ioeWLx4sczUYpabLyVC5qZhNGN0LBhIIPK1zUnRoNcL7iYCSbtRS8TA008haJ9fJF997lSHBxKycKccLCekEGGiNQLKBD2xStjEjHQFyh4aNWokBXxG9UgYrF+/vtkWrVGacPLXX3/JmDFjTPUx5UqIWdm6daWLbxpGMHjWGVFhpsQh+EDTKIaIsBKsoEWUkwTtwIMyfdSpERcyS/QIm5jRG2n+/PnSnrRmH+hMSa1YoUKFTJFqvEEaxk4CL66QSYUKZnalggFq/NKEucW8qas9mEqaVgVYaCTSWkGLGLhhe/Z8KKefPtVdI7Jpj2Mt58mjrJBlA8JWaE4Ba+HChU1XTfxqRjFLlChhYmV0Wn3yySdN6+itW7eaHvn+4IayeOjzcu9lHbiXH0+aJHm1dUYmP0XKF2kL63rylcJIRe3C5tXvi8qdW7Zp15XFknmYFemnn36SFStWpCjWLljwCW2JNXMfkTnzg1x/fegJpJbYQntOmBvB8cUXX5j4V7AsW7ZM7rvvPqlTp468+OKLKdzPtKABXKijn6GeG6R1DK2vH3/kEadTH+eSM6cUbdhQxg0b5u4RHP/973+lIR1P04LgLQMBZGRrQfv+2mulNi1OQyDc158aoR4T7fMi2L5EW9IsP1OhcRLX66Wrc9eHxx93ajLTIzu+Z6EQq8ewf1hHMz0QIiyrdu3aSY0aNeTZZ58NWshiAVxj5rwUgp0ImV7ynHWWtCDOFQkY4bz/fqehlrZsy8yb54x0WoICAaNW9nGtSHgBI0eOTFfIcuY8IhUqLDH3wYxyhim/zJI1hF3M6KpJSkarVq3MMmTIECnmzbkVJ5CGseqjj050wyhZUu7q0kXKRrKfMZUS3boZMTuVKX4QU0uq7Nq1S+bMmXNcwGiQ6T+RTEpOCBkxsmefzS1t2x49OW3DClrcElYxI142fPhwefjhh7XX9IxZcsdSj5AgIMY3W4uZqd9DyEjDaN1aro9GHIsE29tukxxYaPyq3Dw9iwPzLFBO9thjj5k5SEkBSlvARC688EK55JLn9D1HyBi17Ns3x/Fg/0mjnFbQ4pawiRmu5bRp04xLiTVGrIzRyzyBpqCJUUgfeYvZHWh/7bqXZevUka5+I7QRpWlT2UMNDNOTIWbhKhaMU3wFjDkVyFtML9cJAevUqZO8+eab0rjx07JkiaNcqaVf+AtauCoALNElbGLGVO9YZZUqVZK1a9eagP/AgQOPL3yxGF2KZXAvd/G37BWEly8vd3fuLAWiPCnJThJs+RNA0HA3Eyx+Rmua2bNnS8+ePYMWMFpSewL29NNPS1JSkpkdy6sASC+PzBM0b79wVgBYokPYxIwsZ0aQli5dqr8MT5lYhu8ya9YsOUQpUIzy3nvvyZIZM5yZVxGz006T1vqHVI/s/ShziNgcc34hZjR/TID42Y4dO4yA9dCKwp8ficormSYpDbDAyPljDgZEzxMwfxCq57SnmV4eWbD7WWKTsInZDTfcYFzN1BYSaik+j0XIQxpLNwzmDNPnSiEy3TDa33yzu0cWgJhhHhA/w9WM89rWQFA1wp8cAkYOIgK2yus1nQq1a9c+LmBYYHzvmFwkPWg0GwzB7meJPcI6ABCIjHSzjCZYiyZZlx8RQqaXPJUrS5cOHdw9sgg61CJoiBnLnDnuhvgGAZs5c6Y8+uij0rFjRxOjDEXAGFQKVsAsiUXExSzUbpbRhjjZauZU9NIwSpSQjvfcIxXpw0bfE6xJ3L7SpaUmvYLJCUurnwv9UZgNwz2uzvXXO21+ihYNfBxBGlJX6G3GDBn69rxGjZz12o0SEgdxN3G54lTQqAjxFTBy+ChxSwsrYJZQibiYxTII7RzSMMjrQshIw9Cu5XUIEGKEKBGIR6C0pZSfPsjMRIGgIUD+I7UMFLAeEXSPy4OAUZPKLcexeDWqJBIzwSLChSUG+rYw4sl6tmOd8boIGrNMxLil60GBPnFIxAhRClbAEDsvtccKmCUUElbMmJnaNFv0usbqpay2hO7p0sURMfLj2MZjLCYau5PYylAXOWgIkLcfIGSIGMJHb2G6zyJsHMfxTzzhzMmPGLIftxzD/mSrN23qCGDduk58DHFjO/3SPHeTqa4RtBjFEzAsMEYWcd+ZJDktatWqZQSMkXAErEWLFtqQtQ0rLaGTsDOaT5o0SdbPmye5/v3XtPZh5vG77r9fmmnLrCgdLpjFhy6ypEXwGFFhgIDHNFacMEGSL7lEtm3YIH/rdaeff74UwIIi/oYA0gmDJoxYeMyXSS80osv6x3707LNln35cSG/LxTR0NLSkowb5bAsWON0zpk6VZC1sW3/7TX7/9Vc5Y/JkyaeF4ZgWuHXaDT6IWxoDkInPAArlQ+kJl8dZZ51lZuM+99xzrXBZwocKAYQvVDJyTIinZQjldd59912VdOGFqmmxYmYW8qSzzlLjXnvNmb752DGlNm1SqnZtpXLnVmr0aGcdHDzozIzN+iZNlNq505nSmWmlk5OVWrhQqaJFlapYkRNy1sG+fUo9+qhj/7VsqdTevSemrB42TKm77nKem+fimP79nWm1jxxxpsjeutWZMrtxY6WaNVPq9dedY32I1mfDMX/88Yd5Dx955BGVlJSU5nLxxReb2yeffFLNmjVLacFznyl1onktoRKNYxL9+iHUY9g/4dxM8uHG0ZFPu3ym2eIpp8j511wj7ZmRFZcRt5BZyumWQQNGrDMaKGoLZC9Jv1hPxNSYQ4xSGtxEYmB00aURO/vQWeOyy8wMsOt4HuJlvXo5M1xQXYB1x+vw+lh7WCe4rTyP55ayj9eiG6pXd56T2BnWWxS6l/pCdYQWMBMD69y5s+nzll4MDBfyev1eDdPvR79+/YwLWaFCBXerxRJeEkrMDhw4YH6EplbFsZMkj3YFu951l7MDQsGCiJA5iWghcIx0arfxMLeIF4F53EgGDhAf1iFSNFjkGESHxFt9bGlcTfYhfvbJJ44IVanivA7ngPuKe8bU157AERvDteW12c+DVkI8L0sUYmcI2PTp000MrIt2nRn5Tc+VrFmzpskZ8wSMzsPZaYYuS+ySUGLGj/E3rBom49WicaRwYbn7vvukomctsB4rTFseRnSIY2FxuekTxbCYdu50WgORac6AAOIDzPbDwACdYxkYQODy5JECjF56I5VAIB/h2rvXeS0C/xzLFD685uDBIkOHipCwi2j5Vk1Qs4mFhsAxmXA6llFGoHmmr4BNmDAhXQuMNk+egFGbe6N+36yAWaJNwojZp59+Kh+ShrF9uyNA+fPLeVdeKdf6do1lPeVMiBLWEfdxERl51FZTjqVLRdq1c1zQu+92xIVjsKi8HzxBfgSQauVzz3W2IXrUydCEEWFjHZYdLimpB5MmOS4rI5lTpkgyBeaUUbEd8fPF1zrDEgwDjOzSJAAB69q1a1ACdoG2XD0B69+/vxUwS5aTEGKGa/Q23TAYOUR89FK2Vi1piVWUFqRKEMd6/HHH5aMV6bJljlCRaoH1hagA4gR//eXExh57zLHomOkcYezTx7HCEAlPIDmGUU4sw1mzHGvtyy9lHakbCJ/3nL5QOY1ViMhlQswQsM8++8wI2D333CMTJ05MV8Cqa6vwuuuu04bjUK3Nz1kBs8QUCSFmuJf/MKWbF6fSYtBZ/4BP9U969QXrybOgiJXhPlat6riIPXs6AX0sMMSO7QgW0GCRgD4Z+7iN5Jxt2OAMHOAaIoyIFoKGGALuLeK1a5e53c6gQGpwTlhniBlW5sKF7ob02bx5s7zzzjvHBezjjz9OV8DOP/98U8SNgD3//PNy6aWXyhnBzBVqsUSZbC9mxH+WMq88mfNYUYULy80dO0qdGjXcPVIB0UO4OOaVV0RwMXEFESSsLawz4luICq4jVhjoH7+8+qqTY6ZFaocWEFMORe4YAwMMApAkiwhi7WUEyp0QQ147nQJ0XwG79957TX5degJ2nnafPQF74YUX5KabbrICZol5srWYUa40wU3DMOKkxaP61VfLHaRhpAUuIEF8RIq4GYu2wnaTLkFcCyFj+9SpzkgkFh6jlYCLSVIt1poW0A1MzkoQnyRXrDusMqw2LCzfgYFQ4LU864zaV67PB9zqqfrcMipgAwYMsAJmiTuyrZgxezrupTDFmBsny6NFpiuB+9RAlEqUcOoniVtxSxoGFpoWNDLxjatKkJ/gP1YXgwXASCd4JUoIjX7NIwgZ98G/vwyCllGwzrgunlu7ixRzM/cCAkaX38mTJ6crYBX1+0H76ddff90KmCXuybZihpCtIfkVIeJHX7KkdLr/fjkjtcJlBAjhIg7GiGW1asx577hzrgvJFHgGXE9ExBM98FqTYqkRA+P59P65cCc9C8wTF8+99AYPMoJ+vU2VK8sUbZU9OmiQ9oRfMWKWnoBVrVr1uICRetGyZUsjahZLvJMtxWzhwoUyzy8N48o2baTpFVe4ewSA/VgQJ+opcQUpREeIEDQtQCYBFnFiMAGhO/tsxyLjOOJouKDUlHIsAqhftwSWDhYfVhzxMkYiSbtAyDIgZhv180yZNUseffJJ6fbddzJl61ZZvXOnnJJGS3JqID0Bo525FTBLdiTbFZrTuWEMXWN/+klyuqOX+bVLeL+2ytIcvdSU1z/68toVzEX6BZn8MGaMSIsWjqghPvQ+Y4Je2lmPHi3q9ttNZcCpCB5lTA884MTG9DaT4Io1R7rGQw85MbYHHxTRltQuLbSUOhk3NB3+1Pv+tGqVsbq2rF0rubS1mUtbfzm91A39Goe05UmxvAcpE4xEUtDNbPMWS7bHrdMMiowUjB46dMi9FzwhnpbBO7d+/fqppHPPVUmlSztF5DVrqmUffeQUa/stX82YkXLd9u0nir3HjVMqb17HXitTRqn69Z1bHlNoPmiQUwjuFYNTjL5/v1I9ejj7sFSt6hSse89DcTqvw75//53ytX0Wzmv90qVq8vDh6pGOHVVSvXoqqVo1lVShgnNNLKVKOdfIUqWKalSnjurevbspAF+/fr15L9IjI59nqMdE4zUgOx2T6NcPoR7D/hF3M6M51RwpCN+QfErOFlZUkSLS5u675cJgZ6jA0vHSMSgyx52ktAlIyQAekzv2yCOOteYODpg4GdYZEy+S+4U1R34Z1QKka5C0S4oIVhL7svix4fffjQs5VO/7gLYkp2i3cDWTEfM81IFS/sRrsjCaWr68nKUtyDsHDpRuPXrIyy+/bCZePvPMM91ntFgSh7CJGW2RGzduHPTSu3dvOUj6QpjABZv0xhsp0zCuvFJu1z/ukECcSJ8gwI+biMtKQizPyS2PWc929mPAgG3efWDCYEQVwWLbt9+K/Oc/TsoH+7Av6zXrN21yYmBPPXVcwHYgnIzCpiZg111nBOy1GTNksBY+BMy6kpZEJ2xilpXs1eLwERYMI4mIhF5yn3GG3ONZVaGCCFFQTlAdaw3h0tbaYdYjLqwnWx/h8/AEjfIk1hOv4xgE27P42Kb3Wbdx43EBe/CBBxwLjFicK2Am1ucnYFWuvVbaa6vPCNjbb1sLzGLxI2xiRo4S5TGpLQsWLJAnnnhCTj31VLMkJSVpr0y7ZWGANIzduHOelVSypHTWInF6gDkUgwZXE3HCOiKX7K+/ZNm8eY7IsR6BCwRiR7UBI6kcw4iofo51y5fLFIq5tYA95AkYzxfAAjtKrlqFClJZC9gdL7wgr777rgwZO1Zat25tBcxiSYWIW2beLOZMDkxM54i2UpjgokGDBmZ9ZkEkP5o4UXITJ0PIChSQq9q2TTsNI0qs1RbYx4sXy6N9+8pDDz54soBhsXkWGC23tYBVatpUGnXqJK9Ony6vaAG7+eabzSzxFoslbSIuZvny5ZM1a9aYpE7mqKTbaPPmzeV4AmomWK9FYdzIkSaHK4frXpapXl26UtSdRazdsMFxIbWAPawFbNF778lqrLM0BOxMLWC3P/ecEbBXx40zqSlWwCyW0Ii4mNHdlVbLO7V7dvbZZ8stt9wip5B4GgZwL/dStI1AIGbly8s9998veb2i7yixxlfAHn5YpgwdelzAcuNy+goYMTAtYBWbNJF2/fsbAXtNC1ibNm2sgFkSgl9//VUuuugi/V9+mqkh9ofeg8SE2Yd9gyWiYnb06FEjOPTdL168uHTv3l2KeQXZmYTSnWVMiktQPTlZjhYsKG21+1o72DSMTLJGC5UnYN19BYzp6YiXuQKmfATsDC1gt2kBe2XaNHldvy9ttTtsBcySaFSrVk0eIolcQ2ODDaQeufz5558yePBgYwSxD/sGS8TETGlL6YMPPpDZs2ebgD8nxhRj4eDbb7+VKaRIUCKERZYnj5xeu7a0Y8q2CPL7H384Avb000aYUxMwXwusYJ06cuuzzxoBG6oFDMu0Mp1nLZYEhnDTnXfeKUuWLJFRo0YZw4eFkrsPP/zQlNwx4BUKERMzAv6jKenRhDPg/49227D2/NMwWiQluXuEl9VaqDwBGz5smBPE1292qgJ2+ulyeuPGcku/fkbA7u/dW2699VYrYBaLD8TSH3jgAaMLzHa/aNEiI2KIWbNmzYyYhRqOClttZq5cuUzaQNmyZU1gvk+fPiZORsoGU5PRkmft2rUmJyw90qrNZMbsFfqic+/aZYL+h4sUkRvat5f6FG+HiU1bt8oqLVar1qyRLXo5Zf9+M1mwyf+CHDnEvGn6NjlvXjmiRayYFtTz9AdDX7BymUkJsVgSCOJjL730kpQvX94k0R8+fNikcDHLV8g4lU3BEUy91LZt21SXLl3UNddco7SgKS1i7pbgSe205s2bp5IaNnTqEalNPPNMNeSZZ47XM/rXOKa3+B6zavFipxayc2eV1KCBUwtZrlyKWsimRYs6r125skqqW1d1bddOTZgwQa1Zs8Y9w5MJtcYMstMxiX79EOoxiXT9+/fvV926dTO/eZYBAwaoI0eOhPw67B9WNxNlJaCHBValShVjRubOaGtoP3jO8b5xMk3ZCy6Qe7TfnVGwwDwX8tFHHnFcyA8+cFxI0ih8M/ELFpRDpUpJuauvljbPPCNDpk6VNyZOlNtvv91cq8ViCR3cTUYtoZD2cGhNldFsh7CJmRZHmT9/vnz99ddm5JKOpyVLlhQmkg0HxMn20SeMTHnETLtyXYNo6+PP8RiYFiRSRtITMGJgZbWA3awFr3PfvvLmpElWwCyWMPHbb7+ZOBkQgiIflXUZIWxi5gX8scR8Ry4LFy5sbjMDPey/Z9TQTcOgG8YtnTpJbQq+g8BXwBBZI2Bz5kg+epKlImBlrrpKWmvxwgIboV//jjvusLEwiyWMkH7x2muvGe0YMmSIWbjPOhLsQyUsYuZl+AcqVcqsmP3vf/+Td0aNSpGGUePKK+W2m25y9whMCgHDhdRvEAKm/dXjAqaoQvARsNJawFo99ZQMnjJFRk6eLO3bt7cWmMUSIUjbGjdunBkkbNeunVm4zzpSNkIlLGL2008/mZHLZG01McN1kyZNArb98V2YDXs3llYasH28vjAjZFhkWsxMN4wuXdw9UpKqgOFCUiAeIAZWWgtjyyefNAI2SgsYuS/hyoezWCyBwZXEACKJ/hH9WyUkxdKtWzf90yxopogM1d0Mi5hFCuJkm1BoitWxyrT4dH3wQSnvzYSk8QTsdS16xwXs/fdTFTASWUtdcYXc1KeP3K1FbJQWMfrjWwGzWKIDaVoIGS6lvyd32WWXmSkPKWNiH/b15RltqJCPFoiwiFl67X8CLW+99ZYULVrUfYaTmTt3rnwybRr1DY6QaSG6um1baawvNpAFtgvR8wSM9jyegDHjkhawklrAbuzdW17S1tfoqVPNG1ZBr7dYLNGDgULcywkTJsiV2ivid+g7esl95nqtXbu22Yd9Ocajbt26plFFIEELi5ilBRn7wUKDRZS6SJEi8qA2N7evWeMImSZ/5cpSTIvfo/36BbTAcuCG+glYicsvlxu1BTZo0iQZowUM15YJPiwWS9ZAt5zbbrtN9uzZYxJmSZb1h3UMBrAP+/p22KE6gDLJQIIWcTFjVvFgYA5HRgy//PJLKV26tOTQCr1cX8xSLYa/6O1/btsm04cNk9VaqQNZYMdo9KgFrLi23FpoC+zFiRPlrXfeMQLGVGsWiyV7kJqgRVzMgmHkyJHGraxRo4aZUZtp0kieu+jii+VA7txydN8+OQ13MxUXspgWsFq33y4DtVn6tnZNO3bsaCa7tVgs2ZNAghYTYsYIaKlSpVKYk5BTC1aVs86Svf4upDZDi156qST16mUEbKwWMC4ulHYhFoslvvEVNJL1UY8T0bUsAhG7mhmNAkDw7zPtW5fVt3/rxynHNiwWS6JDY4q///5bciIWwS6ff/55wPVpLcEcQ8A/tYxf1hcsVEg+WrFC9gU41lsidW6+S0ZeAwKtT2uJxrWwRON6stO1sETj3LLTtbBE8nqwzL744gvT6DQm3Mxrr7021RrOrVu3mtSP85lI12KxWFyIlTHL25w5c6Rhw4axIWZPPfWUbNmyxQiXL6zbtm2b6Y0Wr5CQm53ITtdjryV2Se96fIWM2BnEhJgx8vjZZ59JgQIFTFYwZim31HVyP56z862YxS72WmKXtK4nkJBBTIgZUNJAUTn9/ekFvmzZMvnvf/8rderUcfewWCyJTmpCBjEjZh5ehj7T0lksFosv33zzTUAhg4iLGQmwiYydyCR2yU6J1YnyPXv66acDChlEXMwS/cec3cQ8OwkAZXPZhez2PcvI/LphF7Pff//dzMZE62xma+rRo4eZ2DPRIAfmu+++M4WyvBfM3sys5axjW7zCtRDX5LPNSAO9WGDXrl0yYMAAI8wkbF9zzTWycOFC048vHqH+me8W3zE+H35/vhPrxgPEyQcOHCjPPvuseewvZsHoSljFjDeQOSI3bdokI0aMML2HSGijpcd25phMIJgHkLn/gL5szMAOrGNbvEITzv79+8vGjRvdNfHFX3/9ZZoPMGVhr169ZMGCBSZOy+dCLCbe4I/lxhtvNB0maKvF747fH5NNZ7SXfrQhMZ75OJ577jl3TUqC0RUS78MmZlgbfEHy5MkjY8aMMbMR07WVFrjr1q2T92nXkyDQUG7s2LGm4y6zNePjszBHwuWXX262+Tediwf49+R6+FIxP2o8QsY4/+h8L/l+0vWYdjP01Zo1a1bcfS70BiSU4/3mWBAG4FpjGTQDbcDiYia3QHPqBqsrpHGFTcz4ZyCV4qqrrkox8Qc99FnHKAQTGCQC/FtQ0dCoUSPJS2siF9yA+vXrm21MyxdP8KWaNm2a+RwHDx5sGgPEG/TWYwYxhIumBJ67f+qpp8qrr75qZtYm1zGe4A+GJqN8tzy4j6Wyjw7NMQzuPtYVOaU0YuzUqZO7xZlUHILVFT63TM9ozhtHGgX/dpi2Dz/8sLnl35sT4o3m3/zdd9+VyZMnG4VdvXq17N+/332Gk0lrRvNYh0AsC7NU8WPhA6OSgdZGzBHYs2dPU+mAlXbs2DHjCsSysBEkr1SpkvkX5IvHaFKZMmVMLRzdTurVq2dmsI/luKj3HeVz4LwRLtxl2jITb6Kc7vHHH5datWqZ9czRmpHZgaIJcSN+WzQ4xFIh1sQUiMT9Jk6cKIMGDTLizJyUhASIOcUKCA+fB+eKVYzbz/cM7aAxIxU/O3bsML+XUHSFH1zQIHypsXLlSlWzZk2lfVl3jYP+51D6zTXb2CcY9PW694InrXNLjVCPychrLFu2zL3nHF+xYkWlhcxdE5hoXAsEe4wWZHXzzTcr/eNX+gt4/LNevHixu0fqxNK16H94VahQIaX/LNXVV1+tpk+frmbPnq2aN29uPpdYuZ5Q9ufzYH9taZrfDQv3uRa2pUU0rgWCOYaZzbt06aL69etnHmvvxtympivgqyvaggvfjOZMM3f48OHj5qHFAasGqGh47LHHTOyMf5h4ATeG5pnMnENLc/+ec/EEljBxGSwDrBfiLzfccIOJv2BhYi3HW8yMzsx0acaqJEbGrEZ4AXzXmDUtXvG+Z8HqCvuHTcxwqzD1+MJYTkDsQv8zmTkB6aSLOxBPcRncGALjTAEWb/Gk1KB3Hq4yPxIgDYASGX784ZqBPxowFSOuMtfjDTQh0DNmzJDzzjtPnn/+eRNzike04WVug9UV9g+bmKGczKwSyDcnEMk/e0YS4eIZYgKkZLRq1cosxAfi6T0gsMpIEl08+XHw78dCftaPP/5oBjiwCFatWuUeEdtoF9PEarzBC2JoHnx/sULj6c+Y39qKFStMagbxJQ/+dOi+qt2vuBJnXzwxC1ZX+K2FTcx4UlwqgsHeiQBfEL7sBCyzyz97MHDdw4cPN4FL8mJY4u36+Ufs2rWr6Wjiu+CiIQpc39ChQ1OMMsUyJUqUMAFm7zvqO8UZPwymPkTw4pHs5hEhTpCarmBV++oKv7ewiRkjRjRIwy3x7UvGKBjrGFXJnz+/uzZ7w5tOGgMuJdbYfffdl+KHEy/wr4jlxeiy78LchXyWuM1YZ/EiAIyYXXrppSa2hNXi5coxYkbCLNdDhnm8wKh59erVTZzMc5mBuB/XSP5ZPKbQgCfOqekKI86+uoIXETYxw/0g7kDKBUPEDJl6iYmoJ2ZvosBQOFYL/yi86S+++KIp1fCWN998M+ZzgFKDf8B4BXEmkxz4Xk6aNMkkXZLfRCoAVig5Z/ECliQJp1QxkDs3c+ZM0yKH62Hdgw8+mOZE27GMZ4UFqyvkEIZNzADXY+rUqeaWEZa+ffuajHd+vNmpqDc9li9fbuoWSQakiy45TL4LAfVYz2NKDV8LIB4hWRZLBouS7ycigCtD0mY8zu7VtGlTE9cEfuDt27c3idrMBH7ZZZeZ9fFOMLrCYAgKGDQZyTHJCPrc3HvBE42cmWhdfzSuBTJyjDb13XvBEcvXkhGicW7Z6VogI8esWLHCvRccvEZYLbNAkAGfyGD+ZicIxGYX4q2kLC3iNQUjNXD7QyXiYhbPiXvhgHKZ7ARJjNkFwgDZhe+//969l7hEXMwsFoslGmS60DwSMPyvz8t9ZLFYLEHgxs+CIlrBvxBPyxCNc4vW9WenYxL9+iHUYxL9+iHUYz7//HP1f7qoOXuw3ueyAAAAAElFTkSuQmCC[/img]
Aufgabe zum gleichseitigen Dreieck
[b]Die Punkte A(0|0) und B(6|–3) sind Eckpunkte des gleichseitigen Dreiecks ABC. [br]Berechne die Koordinaten des Punktes C.[/b][br](Diese Aufgabe knüpft an die Lernumgebung "[url=https://www.geogebra.org/m/fdsh23km]Gleichseitiges Dreieck durch Abbildung (A2)[/url]" an.
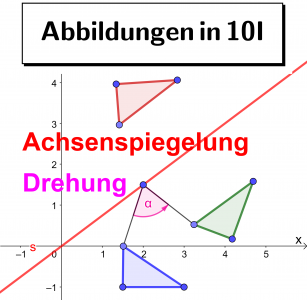
Achsenspiegelung am Beispiel Trapez
Aufgabe:
[b]Die Punkte A(2|–1), B(6,5|–1,5) und D(1|2) sind Eckpunkte des gleichschenkligen Trapez ABCD.[br]Die Ursprungsgerade s mit der Gleichung [/b][math]y=\frac{1}{3}x[/math][b] ist die Symmetrieachse des Trapez ABCD. ([/b][math]x,y\in\mathbb{R}[/math][b])[br][br][br]a) Zeige mit Hilfe der Werkzeuge [icon]/images/ggb/toolbar/mode_midpoint.png[/icon] (Mittelpunkt) und [icon]/images/ggb/toolbar/mode_angle.png[/icon] (Winkel messen), dass die Gerade s die Mittelsenkrechte der Strecke [/b][math]\overline{AD}[/math][b] ist.[br]b) Zeige rechnerisch, dass die Gerade s die Mittelsenkrechte der Strecke [/b][math]\overline{AD}[/math][b] ist.[br]c) Erzeuge den Eckpunkt C durch das Werkzeug [icon]/images/ggb/toolbar/mode_mirroratline.png[/icon] (Achsenspiegelung).[br]d) Zeichne das Trapez ABCD.[/b]
Weitere Abbildungen
[b][size=150]Mit welchen Abbildungen kannst du die Koordinaten der fehlenden Punkte bestimmen?[/size][/b]
Parallelogramm
Der [b]Punkt D[/b] wird berechnet mit der ...
Dreieck
Der [b]Punkt R[/b] wird berechnet mit der [b][color=#38761d]Drehung [/color][/b]und der ...
Aufgabe 1
Berechne die Koordinaten des Punktes D.
Aufgabe 2
Berechne die Koordinaten des Punktes R.
WeMaBy 10I 159/3
b)
B[sub]n[/sub] und Trägergraph
c)
Intervall für x
d)
Punkte C[sub]n[/sub]
e)
Trägergraph h[sub]C[/sub]
f)
Maß des Winkels B[sub]1[/sub]A[sub]1[/sub]D[sub]1[/sub]
g)
Flächeninhalt des Trapez A[sub]1[/sub]B[sub]1[/sub]C[sub]1[/sub]D[sub]1[/sub]