[center][b]The Poincare Disk is one of many models of hyperbolic space. [/b][br]The four most common models of Hyperbolic space are: the Beltrami-Klein model, the Poincaré disk model, the Poincaré half-plane model, and the Lorentz or hyperboloid model[color=#0000ff][br][/color][color=#38761d]The Poincare Disk is a model of [br]2D hyperbolic geometry in which all points are inside the unit disk. Straight lines are represented either by circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle.[/color][/center]

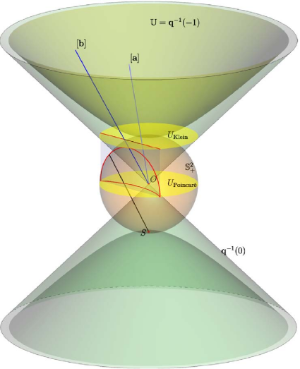
[center][color=#6d9eeb]The large blue portion is a hyperboloid used to display hyperbolic space[/color][br][color=#ff7700]The orange ring is the Beltrami-Klein Disk [/color][br][color=#9900ff]The purple disk is our Poincare Disk[/color][/center][br]The parabolas created in the blue hyperbolic space are projected as straight lines on the orange Beltrami-Klein Disk, but they are projected as arcs of a circle on the purple Poincare Disk

[list=1][*][color=#38761d]A line is represented as an arc of a circle [/color][/*][*][color=#38761d]Diameters are also used inside the disk[/color][/*][/list]

[color=#38761d]A line is represented as an arc of a circle[br][/color]

[color=#38761d]Diameters are also used inside the disk[/color]

This can be created from any point along the boundary of the disk