IM Geo.3.5 Lesson: Splitting Triangle Sides with Dilation, Part 1
Here’s a triangle [math]ABC[/math] with midpoints [math]L[/math], [math]M[/math], and [math]N[/math].[br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUgAAAEDCAYAAABXi52cAAAgAElEQVR4Ae1dCdhV0/q/NE8qlQapiKSBlFBuKo0izSFNpAhJSKY0IKSZy5UhPaE0J4k0XmQss8itbqgbcQtFaVj/5/f2X1/nfN8537fPOXtYa+/f+zznOefsYa33/b3v/u291/CuvykKESACRIAIJETgbwm3ciMRIAJEgAgoEiSDgAgQASKQBAESZBJguDl8CKxatUp17NhRlSpVSv3tb3+T7759+6pdu3aFz1ha5AoCJEhXYGQhpiMwYsQIIcU+ffqoBQsWKJDltGnT1ODBg01XnfoFiAAJMkDwWbU/CEycOFHIEYRIIQKpIECCTAUtHmsdAnh9xis1nxStc50RCpMgjXADlfAKAf30yHZGrxAOd7kkyHD7N/LWNW3aVHXo0CHyOBCA9BAgQaaHG8+yBIGSJUsqdNBQiEA6CJAg00GN51iDAIbzkCCtcZdxipIgjXMJFXITgapVq7KDxk1AI1YWCTJiDo+auWh/RC82O2mi5nl37CVBuoMjSzEUgS1btsgYyHr16qnVq1cr/Mf3pEmTDNWYapmEAAnSJG9QF08Q+PjjjxV6s9EeqT9nnXWWJ3Wx0HAhQIIMlz9pDREgAi4iQIJ0EUwWRQSIQLgQIEGGy5+0hggQARcRIEG6CCaLCgcCM2bMUM2aNVO1a9dWd999dziMohVpIUCCTAs2nhRWBObPn5/VkaM7dPr16xdWc2lXHgiQIPMAiLujhUD37t1zECSI8s8//4wWELRWECBBMhCIQAwCnTp1SkiQv//+e8xR/BkVBEiQUfE07XSEQP/+/XMQ5OWXX+7oXB4UPgRIkOHzKS1KE4F169apAgUKqGOPPVZVrlxZFS5cWMjy5ptvTrNEnmY7AiRI2z1I/V1BAHO1S5cuLYT44IMPZpVZrFgxVahQoaz//BEtBEiQ0fI3rU2CwCmnnCLkePXVV8cdMX78eNnetWvXuO38Ew0ESJDR8DOtzAWBxo0bCwledNFFCY+qWLGiOuaYY9TOnTsT7ufG8CJAggyvb2mZAwSuvPJKIcdatWolPXrJkiVyzAUXXJD0GO4IJwIkyHD6lVY5QGD48OFCfOXLl1cHDhzI9Yw6derIse+//36ux3FnuBAgQYbLn7TGIQKzZs0SwitatKj6/PPP8zzr+++/l+Nr1KiR57E8IDwIkCDD40ta4hCBjRs3Ss80hvO8+OKLDs9SqkWLFkKS06dPd3wOD7QbARKk3f6j9iki8Mcff6iyZcsK0d17770pnq2ks6ZcuXIpn8cT7ESABGmn36h1mgicfvrpQo49evRIq4S+ffumTa5pVciTAkWABBko/KzcTwSaN28u5NakSZOMqsUMG7RdUsKPAAky/D6mhUopDABHVp7TTjstYzxGjRolZfXq1SvjsliA2QiQIM32D7VzAYGHHnpICA1tj2iDdENQVr58+dSePXvcKI5lGIoACdJQx1AtdxB49dVXpWMF86nfe+89dwpVSs2cOVNIN9nsG9cqYkGBIkCCDBR+Vu4lAlu3bpW2QkwTfPrpp12vCq/reG3fsGGD62WzQDMQIEGa4Qdq4TIChw4dUhUqVBACu/32210u/UhxGGAOgsQsG0o4ESBBhtOvkbeqbt26Ql5dunTxFAud6GLevHme1sPCg0GABBkM7qzVQwTatm0r5Hjeeed5WMuRog8fPix1VapUyfO6WIH/CJAg/cecNXqIwMCBA4WwTj75ZA9riS+6W7duUid6yynhQoAEGS5/RtqayZMnC1GVKlVKIUO4n4KlGkqUKOFnlazLBwRIkD6AzCq8R2DVqlUyLhFEtXLlSu8rzFbD0KFDhZwHDBiQbQ//2owACdJm71F3QWDHjh2qePHiQlBTpkwJDJWSJUuq/Pnzq4MHDwamAyt2FwESpLt4srQAEMAKhBhuM2jQoABqP1rl1KlTRY927dod3chfViNAgrTafVS+QYMGQkrt27c3AowqVaqIPtu2bTNCHyqRGQIkyMzw49kBItChQwcho/r16weoRXzVb731lnE6xWvIf6kgQIJMBS0eawwCt956qxDRSSedZIxOWhH9VLts2TK9id+WIkCCtNRxUVYb86rR5ohhNT/88INxUPzyyy+iX9WqVY3TjQqlhgAJMjW8eHTACHz44YcKQ3nQW4xMPabKpZdeKiQZZK+6qdjYpBcJ0iZvRVxXDP7GIHA8PY4dO9Z4NJAvEvpS7EWABGmv7yKnOaYPghz79+9vhe033HCD6HvLLbdYoS+VzIkACTInJtxiIAKNGjUSsmndurWB2iVXqVixYrLEbPIjuMdkBEiQJnuHugkCl19+uZAjUpjZJuPHjxfdO3fubJvq1FcpRYJkGBiNwD333CMEU7FiRaP1zE056I6s5ujdptiFAAnSLn9FStuXXnpJiAWvqd988421ti9ZskRIHs0EFLsQIEHa5a/IaIt1XrDQ1rHHHqtmz55tvd21a9cWknRz4TDrQbHAABKkBU6KmopYmrVMmTJCKFiDOgyyadMmsceNdbnDgIctNpAgbfFUhPSsUaOGkEnv3r1DZXWLFi3Erueeey5UdoXZGBJkmL1roW3NmjUTEsF3GAWdNeXKlQujaaG0iQQZSrfaaVSfPn2EHGvWrGmnAQ601jaid55iPgIkSPN9FAkNH3zwQSFHPF3t378/1DYXLlxYFSlSJNQ2hsU4EmRYPGmxHYsWLZLeahDH+vXrLbbEmeroeMKUyauuusrZCTwqMARIkIFBz4qBwNatW1XRokVlvOP06dMjA0rZsmXlprB3797I2GyjoSRIG70WEp0PHTqkypcvL09Td911V0iscmbGzJkzxe7mzZs7O4FHBYIACTIQ2FkpEKhTp46QBOZaR1EwJhKv2l999VUUzbfCZhKkFW6yV8m1a9eq3bt35zCgTZs2Qg6NGzfOsS8qGz766CPBALNsKGYiQII00y+h0ArLISCHI7LwfP7551k2XX/99UIM1atXz9oW1R+4QeApcs6cOVGFwGi7SZBGu8d+5d5++22FtVmQWRtJGyZOnCiEcPzxx6s9e/bYb2CGFmBaJQjS5mxFGUJg9OkkSKPdEw7l0FPdpEkTIQIknyhYsKACcVKOINCtWzfBBmNBtfz0008KmcgxBIoSHAIkyOCwD23Nw4YNU0gQ++eff2bZuGPHDlloC09Lbdu2zdrOH0cQwEJkxYsXlz8gSqR4A1ZDhw4lRAEiQIIMEPywVj1t2jS5uM8555ysPI6VK1eWbQ0bNpRvDpKO9z6IEISIpWzxjSmJGzdujD+I/3xHgATpO+TRqHDFihWqQoUKMs5RD2fp2LGjGP/EE08ICeC1+7vvvosGILlYuXDhQnXuuecKJkhm8dZbb+VyNHf5iQAJ0k+0I1YXnoD0Mq3ozY4VrGl93HHHqRkzZsRujtRvDIHS62fjaVv37l988cWRwsFkY0mQJnvHct3QyYDXRUwlxPfIkSPjLPrss8/i/kftT79+/aSH/6mnnsoyvUqVKoLVtm3bsrbxR3AIkCCDwz7UNeOiBymWLFlS7dy5Uw0ZMkT+gxQoRxDYvHmzOnz4cBwcaJoAbmeffXbcdv4JBgESZDC4h7pWrLuCXtn8+fOrN954I8vWCRMmyMV/2WWXZW3jj5wINGjQQHCKxS7nUdziBwIkSD9QjlAdu3btymp3BCFml7lz56rff/89+2b+j0Fg+/btQpB43aYEiwAJMlj8Q1d7tWrV5OIeOHBg6Gzz0yDdeTN58mQ/q2Vd2RAgQWYDhH/TR+D8888XcmzXrl36hfDMLATy5csnT+NZG/jDdwRIkL5DHs4K9XS5evXqhdPAAKzCUzg6bG6++eYAameVQIAEyTjIGAEku8WFfOKJJ2ZcFguIRwBTDjF3nRIMAiTIYHAPTa0vvPCCLJeAecRbtmwJjV2mGPLoo4/KzadTp06mqBQpPUiQkXK3u8Z+8cUXqlChQgptZZguR/EGAaRCwxREjBCg+IsACdJfvENTG/IYlilTRp5uxowZExq7TDRk/vz5gjM6wSj+IkCC9Bfv0NSmE1Bcc801obHJZEOwLAPaed99912T1QydbiTI0LnUe4MuvPBCuVhbtmzpfWWsQRD48ssvBfNTTz2ViPiIAAnSR7DDUFWvXr3kQq1Vq1YYzLHKhhYtWgj2zz77rFV626wsCdJm7/ms+/333y8XKNayxprWFH8ROHjwoHTWlC1b1t+KI1wbCTLCzk/F9AULFiisJ1OkSBGF1z1KMAgg0zjaIjH2lOI9AiRI7zG2vgYsuoWcjiDImTNnWm+P7QYULlxYblS222GD/iRIG7wUoI54lcYrNZ5ahg8fHqAmrFojMGLECPFHjx499CZ+e4QACdIjYMNSrB5ewovRLI+iHRJP9LErR5qlYTi0IUGGw4+eWNGqVSt5UsHiWhSzEJg+fbr4pmnTpmYpFjJtSJAhc6hb5gwYMEAuwBo1arhVJMtxGQGMiUTTBzvNXAY2pjgSZAwY/HkEgfHjx8uFh9e4ffv2ERZDEXjnnXfET2eccYahGtqvFgnSfh+6asGyZcsk+QSSUHzwwQeuls3C3EegcePGQpKzZ892v3CWyHyQjIGjCOzYsUOVKFFCBiNztsZRXEz+hQw/eM2uUKGCyWpaqxufIK11nfuKI+EtLrahQ4e6XzhL9AwBnc39gQce8KyOqBZMgoyq57PZjaUSQI5du3bNtod/bUAAy+wiaTHFXQRIkO7iaWVpegU95hu00n2i9G233SY3uH79+tlrhIGakyANdIqfKmFBKDw5nnzyyX5Wy7o8QKBkyZIqf/78HpQc3SJJkNH1vXryySeFHEuVKqV+/fXXCCMRDtOnTJki/mzTpk04DDLAChKkAU4IQoW1a9cqtFvhs3r16iBUYJ0eIFClShUhyR9++MGD0qNXJAkyej6XxZ/w1IhX68cffzyCCITX5KVLl4pfuT65Oz4mQbqDo1WlVKtWTS4iLkhvldscK1u/fn3x7+uvv+74HB6YGAESZGJcQrv13HPPlYunffv2obUx6oZt3rxZfHzSSSdFHYqM7SdBZgxh+gUgr9+qVasSFjBx4sSk+xKe4GAjxjjitRpPGJRwI3DJJZeIrydNmuSKodOmTVP4RE1IkAF5HMQIsmrWrFlCDbAPyxy4JcOGDeNThVtgWlJOvnz5FIb+uCFVq1ZVuKFHTUiQAXkcwYbgBRFu2bIlTgtNnphn64Ygd+Axxxwj86y3b9/uRpEswwIErrvuOomvQYMGZaStnu+d7G0no8INP5kEGZCDOnTooAYPHqwS3ZlBntjuhnz22WcKmXnwNPHaa6+5USTLsAiBYsWKqYIFC2akMd5kcCN364adkTI+n0yC9BlwXR0IEO2M+KBXOVZAnvhkKnv37lVlypSR4H700UczLY7nW4jAmDFjxP+ZxJObN2zbICRBBuCx2FcWvF7j7hz7+qLJM1PVkA0cZSM7OCW6CFSsWFGaWHbv3p0WCFjWIROCTatSQ04iQQbgCP3KoqtG8GG9Y0giwtTHpfKNdWRAjpx2lgpq4Tx21qxZEgvnnXdeWgairRxvOlEUEmQAXscry1lnnZVVMwgTM1vwZJmdPLMOSuFHz5495YKoW7duCmfx0DAjoFenxBTTVMStG3YqdZp0LAkyAG/glQUdNLGCuzTGmWUnz9hjnPweNWqUkCNeqyhEQCOwfv16iYtTTjlFb3L0jZjEm0hUJbqWB+hxTYaxKoAwMX8W5Klft2P3O/k9d+5cWSu5aNGi6ttvv3VyCo+JEAIXXXSRkN0zzzzj2GrEZezbjuMTQ3IgCdJnR3788ccSpPiOFb0dPdrpzFjYtGmTAjFiMXkQJYUIZEfgjz/+kM4ajGxwKpncsJ3WYfJxJEifvQPywxNkIsGdGq8z2ckz0bGx2w4ePKjKly8v544ePTp2F38TgTgEdPv0nXfeGbc92R/EI27amPEV+0l2fNi2kyB99iiG8yR7QsQ+tEGmKroBPt1X81Tr4/F2I1C4cGGFT16CTkPEY/ZPsvjNqzwb95MgbfRajM4tW7aUJ8fmzZvHbOVPIpAcgbvvvlti5oorrkh+EPcIAiRIiwPh2muvlUCvWbOmxVZQ9SAQQDsk2qv37dsXRPXW1EmCtMZVRxSdPHmyuuaaa1Tnzp2FHMuVK6cOHDhgmRVUN2gEpk6dKvGDWVs33HCDmj9/ftAqGVk/CdJItyRWSs+OQcM5PngC+OSTTxIfzK1EIBcENmzYIPGjYwnfw4cPz+WMaO4iQVridwzdiQ1m/btv375q5MiR/BCDlGIAa6DrGNLfyPrz119/WXJF+KMmCdIfnDOuBXNhdSDz+8gTNHFwH4f//Oc/GcdqmAogQVrizY8++ighQWZPtmuJOVQzYAQee+yxHPEU5RkzydxBgkyGjGHb9RojyAyun5w6depkmJZUxxYE+vXrlxVHOp4wKoISjwAJMh4PI/8hZT6CuHr16mrPnj3qgw8+UC1atFBly5ZVP/74o5E6UylzEbjvvvsknp588km1bds29emnn6oCBQooZB+nxCNAgozHw7h/jz/+uARz6dKlFebSakHvNUjztttu05v4TQTyROCpp56SuBkyZEjcsVgjHfGEIWSUowiQII9iYdyvf/3rX3JnR+/iO++8k0O/3r17S1Bj3RkKEcgLgVdffVXiBc01iQQ5ArB2EeUoAiTIo1gY9et///ufJNHFXR13/USyc+dOCXgkIKAQgdwQQAIU5Ag97bTTkh42fvx4iadWrVolPSZqO0iQhnocGVRAjrfeemuuGiIrC45bvnx5rsdxZ3QR+Omnn1SDBg3k6fDw4cO5AlGlShWJp++//z7X46KykwRpoKexdghIz2kvNV7BW7dubaAlVMkEBC677DKJp6+//jpPdRYuXCjHnnnmmXkeG4UDSJCGeVnPsW7YsKFjzaZMmSJB/eKLLzo+hwdGA4GBAwdKbLzyyiuODa5fv76cw3XUlSJBOg4b7w8cOnSoBCZec1IVvJJjyQYKEdAIPPDAAxJP48aN05scfX/11VdyXuXKlR0dH+aDSJCGePe5556TdPjHHXec+vnnn1PWat68eRLUUV2eM2XAQn4CktqimSbdNdEvvvhiOX/ChAkhRyp380iQuePjy16sOIcMz/nz51fLli1Lu87GjRtLTyV6wCnRRQAxBHLEEgnpyv79+6VTBzfsKAsJMmDv7927V2bEIKAzffp799135cJwut5IwKazeg8Q+PLLLxWaaE488cSMS8egccTlTTfdlHFZthZAggzYczVq1JAgRNJSN6Rr165y53fSY+lGfSzDHAR2796tGjVqJPH0+++/u6IYph9iGmJUhQQZoOd1Atx27dq5psXWrVvlAuGUMdcgtaYg3BzxxLdu3TrXdEauUZSJoUJRFBJkQF7v0aOHBJ4XKab0vNo1a9YEZB2r9RuBwYMHSzzNnDnT9aorVKggZf/666+ul216gSTIADyks6lUqlTJk9rRwI67/qWXXupJ+SzULATGjh0r/h41apQnik2fPl3KT2VsrieKBFAoCdJn0F9++WVZCwRtO15mb37kkUckqOfMmeOzhazOTwQwOQA3w6uuusrTavXa62+//ban9ZhWOAnSR498++23qmjRotKJsmjRIs9rPuGEE1QU7/qeA2tIBatXr5YOFD98rEdInHzyyYZY748aJEh/cFYHDx5Uui3noYce8qXWGTNmyNPFP/7xD1/qYyX+IYCbLRIoly9f3rdKmzZtKvGEJWOjIiRInzytX1GQ6t5PwfRDrH3s1rAPP3VnXYkRQOJkTVY7duxIfJAHWzGMCEt+HH/88R6UbmaRJEgf/NKyZUu582KZBL9lxYoVUjc6hijhQECPgEBCZb/liiuukHgaNmyY31UHUh8J0mPY9WyEWrVqeVxT8uKRQRpTGTdt2pT8IO6xAgGd0OSZZ54JTF/EUqFChQKr38+KSZAeov3www/L3RadJUGKzs5y/fXXB6kG684QgUmTJkk83XHHHRmWlNnpt99+u+hx+eWXZ1aQBWeTID1yEtb/QPKJIkWKKMyPDVr69+8vQY3eSIp9CGC4FobzdOzY0Qjly5QpI+2RGHMbZiFBeuDd//73v6pEiRISQF7MbEhH5V27dskF5jRLeTp18BxvEFi7dq3caL2YdZWuxnq1TUyXDbOQID3wLhKN4m4/YsQID0pPv0joA738GIOZvpY8MxYBzK0//fTTJeNT7HYTfp966qkST2FeVZME6XKknX322RI0Xs9sSFft4sWLqwsuuCDd03mejwgcOHBAYYVB3NRM7GB7/fXXRTcQeFiFBOmiZ9FbjGA2+bVDLxwfpcG+LrrY16L69u0r8bR06VJf602lMr3AnClNSano7uRYEqQTlBwcc+ONN0ow57busINifDkEd3y8Hu3bt8+X+lhJ6gjcc889Ek+TJ09O/WQfz9iyZYvoGfRIDa9MJkG6gKxeVRA9e3/99ZcLJXpbxOLFiyWosagTxTwEnnjiCfEPbro2iF5WdvTo0Taom5KOJMiU4Mp5MBIGYF1qDJz98MMPcx5g6JbmzZsrrDfy3XffGaphNNVCBxqaadq0aWMNAMgzgKzjSMQSNiFBZuBRLI5VqlQpGc7z7LPPZlCS/6d+9NFHciEOGjTI/8pZY0IEcIPF8LA6deok3G/yRkxCALFfffXVJquZsm4kyJQhO3oCUj8hKIKe2XBUo9R+oacd+oMsKcEisH37doWEJrjh2to2XLJkSUnlFyyS7tZOgkwTT917h3VAbJVt27YJQUZhypjpPtLrUNs8phBp/HDDRXKWsAgJMg1PdunSRQIBJGm76OQHr732mu2mWKv/gAEDJJ7mzp1rrQ1acSw5C5LEAPcwCAkyRS/qifrVqlVL8UwzDz906JC8FmWyyLyZltmhFdaRAaGMGTPGDoXz0HL27NliT926dfM40o7dJMgU/IQUU0gYiraWMK3wNnHiRAnq559/PgU0eGimCDz99NOCOwaEh0mQpBmkj4QttgsJ0qEH0ZGBPHgYzoChPWGTk046SSFnJZ4oKd4jgCaNsLXXadQ++eQTse3EE0/Um6z9JkE6cN3evXslWQACGllMwihYbRH2YTVEircIfPrpp7JsQc2aNb2tKMDS9Rzy8ePHB6hF5lWTIB1gWKNGDSGPm2++2cHR9h6CTqeyZcsqpGujeIPAzz//rPAKivGOv/zyizeVGFAq1kDKly+f2GmAOmmrQILMAzoknsCT1aWXXprHkfbvxhonsPW2226z3xhDLdDT8qKQuLh3794ST7ZMmUwUMiTIRKj8/zY9kBopzKIiSKgLksRrIMVdBHRCk+nTp7tbsMGlFStWTDLrG6xirqqRIJPAM3z4cCGKMDQ0JzEx4eaNGzeK3T179ky4nxvTQwDDeHDjQZaeKInOStS+fXsrzSZBJnAbctsde+yxCsllMQUsaqKfdN58882ome6JvXhiBDmamkTZE6NjCq1QoYLYj2U/bJNIE2Qih3399deSlQQNzFGdXYIGdlzQrVu3ti2ejdN3+fLlgmWUB+Lr8Z7nnHOOcf7JS6HIEiRy12G0f2xbG9I26bvduHHj8sIu1Pv1K+GLL74Yaju9NG7Dhg0KiWRtSKLsJQ4oG0OacNNFR6BNElmCfOeddxSmC2JWjB7xj2wqcCLmxlKUQgJgDEmhpI7Ab7/9pvDEhGV/v//++9QLCNkZa9askWvLtim6kSVIxB+SxephPPoOx9fKo1fmtGnTJKgxFZGSGgKdO3cW7FasWJHaiSE++u9//7tggnWRbJFIESTaFxG4f/75Z5x/qlevLo7DIGlKPAJohqhYsaLCAGeKMwRuueUWiacnn3zS2QkROerHH3+UXAalS5eOs/irr74ytgMrUgSpn4gaNmyovvnmG3HSww8/LMGM8VpR7mmMi9iYP1hRD7jceeedMVv5MxkCaLsGXhxsnxgh5E8FPkizh5vukCFD5D+W/1iwYEHikwLcGimCBM545UFHTPny5RUWrcqfP7/0Wv/73/9WerGkCy+8kGu1xARl27ZtZdoY7vSU5AhgeBgu/iuuuCL5QdwjSV8wSgTD6PTNBMuXmCiRI0g4AYOhdUompC+LTVSKDht03LRo0cJEfwWik87Ocs011wRSvw2V6mmaaGejJEcAKQNxfYEY0WGDZi+TJZIECYdghgychM/IkSPjfIShPzt27IjbFvU/IEdgFcZUb5n6dtOmTRJPWKPo8OHDmRYXyvNfeeUVpZcpwRsJSBIPJ6YvkxxJgsTcalzsmEyv20D4dJT7dYkGdmAWhaQduSMRvxcLbDVq1EiW/jX9aShec//+ffDBBxI79evXV/PmzZOKJ0yYINtMf+KOHEHiAseF3rRp06wI0Rm1sdgQiICSGIF7771XsENafcoRBLDgGeIJT0iU5Agk6tE/5ZRTBDs04ZgqkSLIm266SRyC/I7ZBXe2yZMnZ9/M/9kQwMBnjAKgKKXXJ4r6rKt0YwE3FdxcEl2P6Zbp9nmRIcgpU6aIMzDWkcsKpB9GyKiOoA5rZnWnyOh4wphHSvoIYLYR4umll15KvxAPz4wEQa5cuVLaiAoVKqRMfpz30M+uFn3qqaeqqlWrKkyni6LgbQMXtc1ropviN4xHBpblypUzRaU4PUJPkBhfVapUKekxmzFjRpzx/JMeApog7rvvvvQKsPis9957T2IJHTMUdxBo166dkCSWwDVNQk+QGHqBO9Rdd91lGvZW64PB9Fjl8dtvv7XajlSUR9IJPDljBUikhKO4g8Aff/whq4Wifds0CTVB6nFX3bt3Nw136/VZu3at3Hiuv/56621xYgDGNyKxCRIpr1u3zskpPCYFBK699lqJJ9PWCA8tQXbp0kUA56tQClGa4qGYUoenc6SOC7vo9YkwnZDiDQIYPI4bkEkSSoLERHhcuHi9pniHwObNmwVnLPQVZkHzDOLpoYceCpNVjV8AAA0OSURBVLOZgduGJNbA2aRpvqEjSMz1xBQmdMxglgPFWwT0TCQTM7G4YTkGOOOixRhaivcIVK5cWfDesmWL95U5qCFUBIkpTeg4KFCggEIbGcV7BJBbEwRywQUXeF+ZzzUsXrxYbAv7E7LPsOZaHUaaIJ7q1KmT63F+7QwNQe7du1dhEDjAtSljsV+O9rKesWPHhg739evXy9hZzhryMnISlw1yxHWMG1TQEhqCxHQlgIpXPor/CFSqVElhAHn2bO3+a5J5jZiPD1tgE7M6ZY5nqiW8//77ci0D/6AlFASJMXkgxw4dOgSNZ2Tr169G999/v/UYNG/eXOLJthX4rAc+xgDtg0cffTRmq/8/rSdIPfyiQYMG/qPHGuMQwLxapM7funVr3Hab/vTp00fIEctzUIJD4JdffpEs9sg6HqRYTZAjRoyQYMbMBkrwCLz55pvij0GDBgWvTBoaDB8+XPTHUhyU4BG48sorxR833HBDYMpYS5AYsItBpSVKlFC421DMQOCyyy6ToP7www/NUMihFk8//bToHZWZQQ5hCfwwLKaHdaOCEisJEotHFS1aVIBbvnx5UNix3gQIfPHFF0I0SCRri7zxxhuic/v27W1ROTJ63nHHHeKboDLZW0eQBw8elFUJ0SnDBe3NvE6uu+46CWosgGa6gNBxs8VyABQzETjhhBMknoJY+dA6gtRjpAYOHGimN6mVNHngBtasWTOj0cAFV7NmTYULEAtvUcxEQC/HHERHrFUE2apVK7mTYFU0itkIYKVIkORzzz1nrKKtW7cWHZcuXWqsjlTsCAKnnXaa+GrNmjW+QmINQfbr108Aqlu3rq8AsbL0EcB8+Fq1aik0i5gmOr0W5u5TzEdg2bJlcv0jH6efYgVBPvzwwwJOxYoV/cSGdWWIwD//+U/xG/xnkuisMdnXQzdJR+qSE4Hzzz9f4glx5ZcYT5BY+Qzd/Ojut3kAsl8ONa0ePEFijvz27duNUO3555+Xi6x///5G6EMlnCPw3XffZWXqcn5WZkcaTZBIcY9xjhjvuHDhwsws5dmBILBo0SIhpFtvvTWQ+mMrXbFihehy8cUXx27mb4sQwHRitG1jyV0/xGiCxAwZgPHggw/6gQXr8AiBli1bih+DXFESq+dhGuSZZ57JPKEe+dmPYvfv3y8pDQsWLOhHdcpYgsS4NJCjaWtU+OKVkFWCPJ3wZc+ePQOxbM+ePZJfsEyZMuqzzz4LRAdW6h4CmHqIeOrWrZt7hSYpyUiCxKh5AICMHpRwINCrVy/xKXoj/Ra9rKgJ+QX9tj2s9ZUuXVri6cCBA56aaBxBIrU9yBEDeCnhQQAN7PArxh76KZhbjXr97Pn0076o1vXII4+IXxs3buwpBEYR5JQpU8TocuXKeWo0Cw8GAb2YGnJH+iFjxoyReEKWHkr4EMCYSNz8Pv74Y8+MM4YgV65cKSnusaYMklFQwocAXofQuF6vXj3PjXvhhRfk4rn66qs9r4sVBIPAnDlzxMeYZeOVGEGQmBOLNgWsRvjSSy95ZSvLNQCBCRMmSFCPHz/eM22QCTyI13nPDGLBSRHAzRa+xg3RCzGCILF+NYy89957vbCRZRqGAPyNWVE7d+50XTMsF4reagxQZ55Q1+E1rkCMSgB3YDKCFxI4QerpQ8geTIkGAkh2jKAeNmyYqwb/9ddf6uyzz1YlS5ZUtiXsdRWIiBWmk45ghQG3JVCC7Nq1q1woYVxT2W1Hha089D7my5dPffnll66ZpmdZcNaVa5BaUdDu3btVgQIFVJEiRVzXNzCC1D2a1atXd90oFmg+AqtWrZKbo1udKFgHB0+ljz/+uPnGU0PXEdCLrfXu3dvVsgMhyGeffVY6ZNAxY2IqLFcRZmFJEejcubOQGsgyExk7dqyUc9ddd2VSDM+1HAHkbUBHr5viO0Fi2hmG8mC4B9uJ3HSlfWV9/fXXQmyXXHJJ2srPmjVLynD7ySFthXhiYAjoVSkvuugi13TwlSD37t0rvU14FWKiUtd8aHVBN954oxDcyy+/nLIda9eulXPdvCBSVoInGIUARkeAXzZv3uyKXr4S5Omnny7K+5WqyBWEWIinCPz6668SEw0bNkypnh9++EGVL19eIaaQFo9CBIAAmu9AkLVr13YFEN8I8sILLxTFO3Xq5IriLCQ8CDzwwAMSG5hq6lRAqEii/N577zk9hcdFBIEzzjhD4gm5SDMVXwgSaa7A6qk+JWRqHM+3BwE8DWJuLYZs5CVdunSReJo7d25eh3J/BBF46623JD7cWKLFc4LE4E2Qo9+L7UQwLqw2GW3SiJO8ZlMNGTJEjps8ebLV9lJ5bxFo0qSJxAlGOGQinhIkehixXAIyOf/222+Z6MlzI4DAWWedJSMcNm7cmNDaiRMnStBjDC2FCOSGANZAwkSE4sWL53ZYnvs8I0hk5ClatKgsuJXpOLc8rTD8AKzHotdkSfbbcBN8UW/JkiVCgAMGDMhR37x582Rfjx49cuyL2gbEENbXQaZ0/EY77I8//ii/P//886jBkdReZBzHWwlygqYrnhAkBn9XqFBBlEul4T1dI0w/r1mzZkovFIXeNT1mD+1umjhNt8Ev/dq2bStx8/bbb2dVifGyCPSmTZuqw4cPZ22P6g8MhsZSukj2AVzQPLFhwwb5zWmWR6MCPITph3iSTFdcI0gMu0CqMuR1rFOnjjgLY9woSpEgnUfB+vXrJXaw3Ma0adPU8uXLVeXKlRWmpCJTD0XJbBESpLNIuOWWWySekBQH/JTqkDBXCBKBjDtZ7AfrgFCOIECCTC0S8JQdG0t4Aoh9okyttPAdzSfI1HyKWXux8ZTKJBVXCBJLJMQqgN/I1DN16lR+pk5VNWrUkKdq4FGpUiXVqFEjwQWdV61atSJGMXFy991354glxBNSozGejlxPIEjMY9fJh9FkM3r0aMENb23E6SjvdO/ePUc8IQeEU8mYIL/44oscCmQnS/6Pf7omHsSDMRBsDDhdxyZjgkSjObJoZHc4OiXGjRvHz7hx0n6GVRqBBzqvGjRoIL+BG2YYEaejcaLnZmePp4EDBxKn/7+e8ASJJqxRo0bJdYenpDvuuEN+I30c4+loPCERSvZYQsfN/v37HT1EZkyQqEWvRqgVOffccxUSU1COIMA2yNQi4dprr40LardyRqamhblHsw3SuW9AhGjS0tyEb4yndSquECQqw9oQSFaKlcYo8QiQIOPxcPIPoyGwsBd6sSnxCJAg4/Fw8g/jaB977DH16aefOjk86xjXCDKrRP7IgQAJMgck3JABAiTIDMBL8VQSZIqApXN4r169FD4QfOuB4vjNgeLpIBrtcxA3ixcvlum7+L169Wq1bds2ia1169ZFGxyXrXedIDEmEk9Mu3btcllVFhd2BDAlFbEzePDgpKZi7REcs2DBgqTHcAcRiEUAbY6IGXz69u2rRo4cqZxOf3aVIEGKpUqVkgZRpwrEGsLf0UYAmZ+wZCumFCaS2AkJjK9ECHFbIgQQT/ggvvBBUhR01uB3XuIqQaJCKILKeYfPC3ruz46ADmTETyJByjy9tGui/dxGBBIhkKjnGm8ieJjLSxJHYl5nJdiPebKoEHd2MLQTdk5QDDdFGAEdyIkIEq9JIEi8foNIKUTACQIYEI54yv7GAX5KFGfZy3SNIMHIOnDxnVs7UnYl+J8I6EDGjTZ7QOumGwQ5Y4uxkgoCulkm9hzEU7169RQ4Ky9xhSCzB3UsWealAPcTASCAQEb7IwRPirF3fN10g30gTxxLIQJOEAAXVatWTTpm0DnTsWPHrDcRJx3JrhAk7ur66RFKI6DB0BQi4BSB2JsqYkk30eimGzxhgjRBkE7n0Tqtm8eFFwE09+l4wlst/oMwY2/AuVmfMUHqoEWluisdv5283+emGPdFC4HYdmuQpSZI/MYHopdciBYytDYTBBK9cSC20F/iyxNkLEOjYnwQ0FDMiQKZGM9zw4MA4kXf1RFDuOvjSRGv3XiKhCCuYt9UwmM9LfECAf3wpuNH16G363jT2xN9Z/QEqRtAsyugG9ydKJBIKW6LFgI6YPUNFUPEQIT61UijgbZJkCeFCDhBALGi27Vjj9dvIjreYvdl/50RQSJg9etPjoI5FjI7JPyfBAE9hEfv1oSJ4NZBjG88ZXJ8rUaJ33khgDGzsW8ciKHnn39eXq+T8Vb2MtMmSM3O2Z8edQUIbt7tNRr8zg0BBHJswGoyBHFq0aSZLN70cfwmAhoBPMDhphr7SZWX0iZIvEbn1puIfQxm7Sp+54ZAoljJ3jyDWMq+LbcyuY8IIF5iP+kgkjZBplMZzyECRIAI2IQACdImb1FXIkAEfEWABOkr3KyMCBABmxAgQdrkLepKBIiArwiQIH2Fm5URASJgEwIkSJu8RV2JABHwFQESpK9wszIiQARsQoAEaZO3qCsRIAK+IkCC9BVuVkYEiIBNCPwf3mh3Hh0fxzsAAAAASUVORK5CYII=[/img][br][br]What do you notice? What do you wonder?
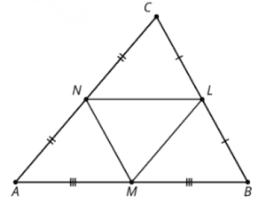
Here’s a triangle [math]ABC[/math]. Points [math]M[/math] and [math]N[/math] are the midpoints of 2 sides.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAU4AAAEFCAYAAACMzA7GAAAgAElEQVR4Ae2dCbiN1f7H63DI1CEz+RuiZIgI4RoqEpKhUpQhUnTKUDTRNZRc3WOoRN1MXREhQ+lx8aBudd3ILNLTI1dXqWuOkFr/5/ur97TPPvsce+93Wut9v+t59rP3ft81/H6ftfZ3r/d913CRYiABEiABEkiIwEUJxWZkEiABEiABReFkIyABEiCBBAlQOBMExugkQAIkQOFkGyABEiCBBAlQOBMExujmEVi3bp3q1KmTKlq0qLrooovkvXfv3uro0aPmOUOLtSBA4dSiGmiEWwRGjhwpYtmrVy+1ZMkSBRGdNWuWGjRokFtFMt8QEKBwhqCSw+ripEmTRDQhlAwk4CQBCqeTNJmXNgRwGY5Lc/YstamSQBlC4QxUddIZi4DV2+R9TIsI350kQOF0kibz0oZAixYtVMeOHbWxh4YEiwCFM1j1SW9+J5CWlqbwYIiBBNwgQOF0gyrz9J0Ahh1ROH2vhsAaQOEMbNWG27GKFSvywVC4m4Cr3lM4XcXLzP0igPubeKrOh0N+1UCwy6VwBrt+Q+vdvn37ZAxn3bp11fr16xW+433y5MmhZULHnSNA4XSOJXPSjMCWLVsUnq7jfqf1qlOnjmZW0hwTCVA4Taw12kwCJOArAQqnr/hZOAmQgIkEKJwm1hptJgES8JUAhdNX/CxcJwJz5sxRLVu2VDVr1lRPP/20TqbRFs0IUDg1qxCa4w+Bd955J/MBkvUgqW/fvv4Yw1K1J0Dh1L6KaKAXBLp27ZpNOCGgP/30kxfFswzDCFA4DaswmusOgc6dO8cUzpMnT7pTIHM1mgCF0+jqo/FOEejXr1824bzrrrucyp75BIwAhTNgFUp3Eifw2WefqdTUVJWSkqIuv/xyVbhwYRHRZcuWJZ4ZU4SCAIUzFNVMJ3MigLnsxYoVE6EcO3ZsZrSrr75a1atXL/M7P5BAJAEKZyQNfg4dgSpVqoho3nfffVl8X716tRyfOXNmluP8QgIgQOFkOwgtgSZNmog43njjjTEZtGrVSpUpUybmOR4MNwEKZ7jrP7Ted+vWTUSzRo0aOTL4/PPPJU7kJXyOkXkiVAQonKGqbjoLAs8884wIYunSpdXPP/+cK5TevXtL3OPHj+cajyfDRYDCGa76Dr238+fPFyEsWLCg2rFjxwV5nDhxQuKnp6dfMC4jhIcAhTM8dR16T/fu3avy588vw47mzp0bN4/hw4eLeO7ZsyfuNIwYbAIUzmDXL737ncDp06dViRIlRABHjBiRMBeM8+zSpUvC6ZggmAQonMGsV3oVReCqq64S0ezevXvUmfi+Tps2TdKvXbs2vgSMFWgCFM5AVy+dA4EbbrhBRK9Zs2a2gFSqVEk1btzYVh5MHAwCFM5g1CO9yIEABrZjlaNq1arlECP+w8uXL5e8Erk/Gn/ujGkSAQqnSbVFWxMiMG7cOBE63NvEPU4nwp/+9CeFPdsZwk2Awhnu+g+s9++++666+OKL5Sn6hg0bHPMTC4KgB5uRkeFYnszIPAIUTvPqjBZfgMD+/fsVxmlCOF9//fULxE78NJaby5cvnzp79mziiZkiEAQonIGoRjphEfjll19kfjl6hUOHDrUOO/p+6NAh6XU++uijjubLzMwhQOE0p65oaRwEateuLaJ2++23xxE7+SgQTYjzvn37ks+EKY0lQOE0tupoeDSBW265RcSsUaNG0adc+Q7hxGIhDOEjQOEMX50H0uMBAwaIaFauXNkz/yZOnChlfvzxx56VyYL0IEDh1KMeaIUNAi+++KIIWNGiRRVWdPcyYIWlFi1aeFkky9KAAIVTg0qgCckTWLduncqTJ4/sGeTHdMgFCxaIaC9atCh5J5jSOAIUTuOqjAZbBL777rvMjdVefvll67Dn7/Xr11dXXnml5+WyQP8IUDj9Y8+SbRLAjpR4QPPII4/YzMlectzjhB1+irc9D5g6UQIUzkSJMb4WBNDLg1h16NBBC3tuu+02VaRIES1soRHuE6Bwus+YJThMoGPHjiKaOm3f+/XXX4tNTz31lMPeMjsdCVA4dawV2pQjAWvgeYUKFXKM49eJhx56SMTz4MGDfpnAcj0iQOH0CDSLsU8A885xeX7ppZeqb775xn6GDueAFZhgHzZ4Ywg2AQpnsOs3MN5t3LhRhhzlzZtXvffee9r6ha2EIZ6bNm3S1kYaZp8AhdM+Q+bgMgEMasfgdgjSCy+84HJp9rNPS0tTN998s/2MmIO2BCic2lYNDbMIYBolRLNfv37WIa3fZ8+eLfZiTVCGYBKgcAazXgPjFfb4gWia1oOrUaOGwkpNDMEkQOEMZr0GwissGAzRNFGA1qxZI7a/9tprgagLOpGVAIUzKw9+04TA8OHDRXjKli2riUWJm9G6dWvZyz3xlEyhOwEKp+41FEL75s2bJ9teFCpUSH3xxRfGEti9e7eI/6hRo4z1gYbHJkDhjM2FR30iALHJnz+/SklJUW+//bZPVjhXrLU98ZEjR5zLlDn5ToDC6XsV0ACLAAaQFy9eXHppo0ePtg4b/X748GHx58EHHzTaDxqflQCFMysPfvORAJZmw8Ognj17+miF80WPGDFC/NqxY4fzmTNHXwhQOH3BzkKjCWAVdYhmy5Yto08F4ju2E9ZlJadAAPXZCQqnzxXA4pXq1auXiGb16tUDi+PVV18VH1etWhVYH8PkGIUzTLWtoa/W3O6SJUuqs2fPamihcyZhBtR1113nXIbMyTcCFE7f0LPgZcuWydPzAgUKqM2bNwceCKZg4nYEpmQymE2Awml2/Rlr/f79+xUE8+KLL1ZvvPGGsX4kanizZs1U+fLlE03G+JoRoHBqViFhMOeXX35R2FYXva+wrZiOnjX8HjduXBiqOrA+UjgDW7X6OlarVi0RD8xFD2O4++67paeNcasMZhKgcJpZb8ZajVWO0ONq0qSJsT7YNfzAgQPCYODAgXazYnqfCFA4fQIf5GJz2tYCs2cgmldccUWQ3Y/Lt8cee0xYfPnll3HFZyS9CFA49aqPQFiDwez9+/fP4sukSZNEKC677DL1448/ZjkXxi8YeoU/kTvuuCOM7hvvM4XT+CrUz4Hx48eLKLRr104dO3ZMYW3KPHnyKMye+eijj/Qz2CeLrD+TDz74wCcLWGyyBCicyZJjulwJvPXWWzJGE7OBChYsKEKK2TMMWQmUKVNGNW3aNOtBftOeAIVT+yoyw8BXXnlFZWRkZDEWvUv0NHFJ2qlTpyzn+OU3Alg6D3zwR8NgDgEKpzl1pbWl2EgNAjBo0KBMO6+99lo5Zi0VN3Xq1Mxz/PAHAUzDxHRMBnMIUDjNqSvtLR0zZowIZefOnVX79u3lc4MGDcTue+65R76HbcB7PJWGnjn+dCZOnBhPdMbRgACFU4NKCJIJ1ta4EIJy5cplce3JJ58UgXj++eezHOcXpTp27KguueQS9euvvxKHAQQonAZUkkkmYldHiCbmoJcoUUKtXr06i/m8XM+CI/PL3r17hduwYcMyj/GDvgQonPrWjXGWbdiwQaWmpspr1qxZqmHDhiIGM2bMMM4XPwxOT08XXphZxKA3AQqn3vVjjHVHjx5VRYsWlR8+xiciYJA3BnijBzpy5EhjfPHLUIx5BSvcD2bQmwCFU+/6Mca6SpUqyY9+wIAB2WweMmSI2rVrV7bjPJCdAO7/QjzRe2fQlwCFU9+6Mcay66+/Xn7smCnEYJ8Aeu433nij/YyYg2sEKJyuoQ1HxnfeeaeIZt26dcPhsAdeYmFn9DrfeecdD0pjEckQoHAmQ41phADGZOIHzhXNnW8QNWvWVEHevM55Yt7mSOH0lndgSnvzzTdlyFHhwoXVvn37AuOXLo5gGBf+lDCVlUE/AhRO/epEe4t27typ8ufPL/PQly5dqr29phqIRZ/T0tJMNT/QdlM4A129zjuH7R6sueecAeQ838gct23bJr3O4cOHRx7mZw0IUDg1qASTTKhWrZr8mPv06WOS2cbaCs64ZP/hhx+M9SGIhlM4g1irLvnUvHlz+RG3atXKpRKYbTSBgwcP8o8qGooG3ymcGlSCCSb06NFDfsA1atQwwdxA2fjMM88I+61btwbKL5OdoXCaXHse2f7ss8/KDxd7oWNPdAZvCZw/f14exrVt29bbgllajgQonDmi4QkQWLJkiWyBUaBAAU6b9LFJYNsR3Ot8//33fbSCRVsEKJwWCb5nI7B//37ZLyglJYVbO2Sj4/2BKlWqqDp16nhfMEvMRoDCmQ0JD4AALslxaY5eDu6xMfhPYPny5VIf06dP99+YkFtA4Qx5A8jJfUz5g2hyibOcCPlzHCMbSpUq5U/hLDWTAIUzEwU/WARat24totmsWTPrEN81IYDl5vCHhv2dGPwjQOH0j72WJT/wwAPyw7zyyiu1tI9GKdWtWzepo5MnTxKHTwQonD6B17HYCRMmyA8SewWdOXNGRxNpk1Lqq6++knqKtWg0AXlDgMLpDWftS1m1apUs2oHFOz799FPt7Q27gUOHDhXx3LNnT9hR+OI/hdMX7HoV+t1336kiRYrIMnHcWE2vusnJGlym415np06dcorC4y4SoHC6CNeUrLEQMX6Ejz/+uCkm006l1OTJk6Xe1q5dSx4eE6Bwegxct+Kw5QVEE7tRMphHoGzZsrINs3mWm20xhdPs+rNl/a233iqiic3WGMwksGDBAqnDOXPmmOmAoVZTOA2tOLtmDxw4UH5wlStXtpsV0/tMoEGDBqpChQo+WxGu4imc4apv8XbatGkimtiG9vjx4yEkECyXcY8Tt1vGjx8fLMc09obCqXHluGHaJ598olJTU+W1fv16N4pgnj4QwNP1PHnyqJ9//tmH0sNXJIUzRHV+9OhRhV4meidTpkwJkefBdxUb6KFeBw8eHHxnNfCQwqlBJXhlQqVKleTHhfubDMEjkJ6eLvX79ddfB885zTyicGpWIW6Z07BhQ/lR3XbbbW4VwXx9JnDo0CGp47vuustnS4JfPIXThzoeOXKkWrduXcySJ02alOO5mAniOIgxmriMq1evXhyxGcVkAuPGjZO6/vjjj012Q3vbKZweVxEEEyLWsmXLmCXjHLarcCo88cQTUh6HqzhFVP98ihUrprgkoLv1ROF0l2+23NHbTEtLEzHbt29flvOWqOIhjhPhjTfekPnnmIeObWYZwkFg1qxZ0r4WLlwYDod98JLC6TH0jh07qkGDBqmKFSsqiGhkwHccdyJs375ddkbEEBVu8OUEUbPyqFWrlqpatapZRhtkLYXT48qCMOI+Jl54yh0ZIKp42Q2nTp1SxYsXl17HX//6V7vZMb2BBFasWCH1j4VAGJwnQOF0nmmOOeISHPcwcUmOy3Trs5XAElXre7Lv1apVk7yxmjtDeAm0adNGdikNLwH3PKdwusc2W8546AOxtAJ6l7169ZKvsYTUipfIOx4KoAz8aBjCTWDjxo3SFvCAkMFZAn/8ip3Nl7nFIIB7mJH7YkNIMZMHPdFoUY2R/IKH7r33Xvmh1K5d+4JxGSEcBPr27SttAotVMzhHgMLpHMsL5tSiRQt5MBQZEU/Y8RQ0WlQj48TzefTo0fIDwfqMDCRgEcAsIlyB9OjRwzrEdwcIUDgdgBhvFpZIRsbHE3YsJgxRtS7bI8/H83nRokUqJSVF7md9+eWX8SRhnBAR+POf/yzi+dlnn4XIa3ddpXC6yzcz9y1btkjjxXtksI7jCTt6nokG7HhYsGBBEU4IKAMJRBM4ffq0uuSSS1SrVq2iT/F7kgQonEmCSzQZRBE9zlgB9z1xORUtqrHiRh47f/68Kl26tKQdM2ZM5Cl+JoEsBKZOnSrt5N13381ynF+SI0DhTI5bwqkwBCmnHiXORQ+Gj6eAmjVryo8h2Uv8eMpgnOAQuOKKKxTaDIN9AhRO+wx9yQGXXeil3nDDDb6Uz0LNI4BbOWgzr776qnnGa2YxhVOzConHnPvvv19+ANWrV48nOuOQQCaB5s2bKywCwmCPAIXTHj/PUr/44ouqT58+qkuXLiKaJUuW5DYJntEPTkEffPCBtB88aWdIngCFM3l2nqW0ZgPhMgsvDD3aunWrZ+WzoGAR6N69u7SjY8eOBcsxD72hcHoIO5mirPtSlmha73igxEACyRDYvXu3CCdu+TAkR4DCmRw3z1JhFSVLLCPf33zzTc9sYEHBIzBs2DBpV7t27Qqecx54ROH0ALKdIjZt2hRTOKMXQbZTBtOGj8Dhw4elXbVv3z58zjvgMYXTAYhuZoGGjZ7mxRdfnCmgbdu2dbNI5h0SAhMmTJA2tXr16pB47JybFE7nWDqe0yOPPCINGwOXf/zxR/Xpp58qrLEJEeUWsI7jDmWG5cqV4yZ+SdQ8hTMJaF4kmTJliogmxtxhrrEVDhw4oPLmzav69etnHeI7CSRNYM6cOdLOZs+enXQeYUxI4dSw1j/88EOVmpqq8uXLp2Jt84rpmbh8//e//62h9TTJNAINGzZUZcqUMc1sX+2lcPqKP3vhR44ckcWNIYyvvfZa9ghKqXPnzqny5cur2267LeZ5HiSBRAisXLlS/ojHjh2bSLJQx6Vwalb9WF4Oovnoo4/mapm12s3y5ctzjceTJBAPgc6dO0u7O3PmTDzRQx+HwqlRE2jUqJE0XjTieEK9evUU0jCQgF0CmzdvlraXnp5uN6tQpKdwalLN1hz0Bg0axG3R4sWLpbG//vrrcadhRBLIicDDDz8s7QmLYzPkToDCmTsfT85aszj+7//+L+HyMKYzen/2hDNhAhJQSmHEBm4T4U+cIXcCFM7c+bh+dubMmTIu89JLL1X/+9//Ei7vo48+ksb+3HPPJZyWCUggmgDaEcQTIzsYciZA4cyZjetncF8Je8FgXOaqVauSLq93796qQIECilvAJo2QCX8ncPbsWVmvs3HjxmSSCwEKZy5w3Dx16tQpVaJECfl3x0IedgJ2tkQvATONGEjALgEMg0N7mj9/vt2sApuewulT1V555ZXSOB966CFHLHjiiSckv23btjmSHzMJN4HatWurihUrhhtCLt5TOHOB49Ypa2Hidu3aOVbEiRMnVPHixVXXrl0dy5MZhZfAkiVL5I8YC4EwZCdA4czOxNUj1urb2BLY6TBx4kRp7HbulzptE/Mzl8Att9wi037N9cA9yymc7rHNljP2ecG9I6xI41aoUaOGatGihVvZM98QEbBGbDz22GMh8jo+Vymc8XGyHWvBggWyV1ChQoVcXRJu7ty5Is5Y9YaBBOwSsHZU/e9//2s3q0Clp3B6UJ146l2wYEGVJ08etWzZMtdLxF7r3DrYdcyhKGDv3r3yR9ytW7dQ+BuvkxTOeEklGe/8+fOyZBcu0ceNG5dkLoklW7NmjTT2jIyMxBIyNgnEIPD0009Le8JC2gy/EaBwutwSatasKY2ub9++LpeUNfu7775bBjJzC9isXPgtcQJoQ5hgwXvnf7CjcP7BwvFPrVq1EtG86aabHM/7Qhnu2LFDysY8eAYSsEtg8uTJ0p6WLl1qN6tApKdwulSNffr0kYaGp9x+hUGDBokNX3zxhV8msNwAEahatarCxA0GpSicLrSCv/zlLyJYpUqVciH3+LP8/vvvFZ7i9+zZM/5EjEkCORCYN2+etOtXXnklhxjhOUzhdLiuV6xYIYt24J7Qrl27HM498eyef/55aexc7SZxdkyRnQDucxYpUiT7iZAdoXA6WOHffvutNCps3/vWW285mLO9rKpUqaLatGljLxOmJgGlFPZgxwiR4cOHh5oHhdPB6r/88sulUWEXSp3CjBkzxK6FCxfqZBZtMZTAPffcI+3p8OHDhnpg32wKp32GksO1114rjQmNSseA9RXr1q2ro2m0yTACWIELvU6sAxvWQOF0oObbt28vDQmrHuka3nvvPbFxypQpuppIuwwiMGTIEGlP27dvN8hq50ylcNpkiV0B8e9brVo1mzm5n7xTp06qbNmyilvAus866CUcPHhQ2v3NN98cdFdj+kfhjIklvoMvvfSSNB6sg3nu3Ln4EvkYa+PGjWLvM88846MVLDooBDCFGJ2GlStXBsWluP2gcMaNKmvE9evXy1qF+fPnVxAkU8KDDz4oqzTt37/fFJNpp6YEsA5D+fLlFVaLD1ugcCZR40eOHFFFixaV3SnxxNqk8J///EdWaXrggQdMMpu2akpg+vTp0us07XdgFyeFMwmClStXlsby+OOPJ5Ha/yTWgspc7cb/ugiCBY0aNZKNB4PgS7w+UDjjJfV7PDQS3Ne54447EkypT3RsAYtV6Dt27KiPUbTEWALLly+X38SYMWOM9SFRwymcCRC7/fbbpYFAPE0PmG+MP4B3333XdFdovwYEunTpIu0J216HIVA446zloUOHSsOoVKlSnCn0j4ZB+9dff73+htJC7Qls2LBBfh/9+/fX3lYnDKRwxkERN74x/zwtLU0dP348jhRmRFm0aJE0dtzgZyABuwQgmriKwXYbQQ8UzgvU8KZNm9Qll1yiUlNTFYYgBS1gC1g87GIgAbsEvvrqKxHODh062M1K+/QUzlyqCPdrSpQoIY0hqFMV//nPf4p/Y8eOzYUET5FAfASsERvr1q2LL4GhsSicuVQcVrvGpcfAgQNziWX+qV69eskunIcOHTLfGXrgK4GTJ0+qyy67TF133XW+2uF24RTOHAg3b95cRPPWW2/NIUZwDltbwAb9DyI4Naa3Jy+//LL8dubOnau3oTaso3DGgGetN4inzmEJGMyP3nVYV7sJSz175ec111wj0zG9Ks/rciicUcSxAAYEBHNwwxQwWgCXWHfddVeY3KavLhFYsGCB/I5eeOEFl0rwN1sKZwR/bHeRkpKiChcurLBsVtjChAkTpLFjewQGErBLoG3btjKMD4uBBC1QOH+v0T179sgDkjx58qj3338/aPUctz9XX321atmyZdzxGZEEciKwdu1a+SMePHhwTlGMPU7hVErhH7FMmTJSyRkZGcZWphOGv/nmm8IB7wwkYJcARmzg1hdW5QpSCJVwzp49W2E9yuhQq1YtqVwutfYbGfQ40fNkIAG7BHbu3Cm/rTvvvNNuVlqlD5Vw4kY1/v1w7wVraiK0bt1ajuGd4TcC1hawuOfJQAJ2CVjrPPzrX/+ym5U26UMlnKA+f/58WcgXvczOnTuLaNasWVObCtHFEDxdx1P2IM3N14Vt2OzAxIqCBQuqpk2bBsb1wAvn6dOnVXTP6ZNPPlHFihUT0cRK7gzZCWA8J3rnpi7WnN0jHvGTgHW1t3jxYj/NcKzswAtnv379RAAGDRqUCQ1rUObNm1eGHkEcsDYlQ3YCmEkEPmFY7Sa79zziNAHsBBuUBWUCL5yofKxMDQHApTlWcClSpIiIJpZVu/fee+Xck08+6XQ7MT4/6xILT0YZSMAugVmzZslvDbvDmh5CIZyoJDxRh3jmy5dP3p999tnMunvqqafkWPfu3TOP8cNvBLBqErhhFSUGErBLACM2sEyj6SE0womKqlq1qogAKi56dsy0adMUNy+L3ZxxeYV1OxlIwC6BFStWyG/Q9Cu80AgnVjlCz6lhw4bywueZM2fabQehSG9tAYtbGwwkYJdA165d5bf4/fff283Kt/ShEM6HH35YKgrrayKcOXNGWRuvjRo1yjf4JhWMvYnCtFqUSXVjmq0bN26U32OPHj1MMz3T3sALJ25Eo3eJldx/+eWXTMfxYciQIWrYsGFZjvFLbAIYiQCOHIEQmw+PJkYgPT1d2tOWLVsSS6hJ7EALJxYZwMOg/Pnzq61bt2qC3FwzsA879mPHvuwMJGCHwNdffy0rJ9144412svEtbWCFE1MqMcgdu1P+/e9/9w1wkArGwzP0OrGvDAMJ2CUwevRoaU94YGRaCKxw4kkwfuQYasTgHAEshIKl94K22o1zhJhTvAQwq+/yyy9X1atXjzeJNvECKZx4kAHRxNM7BmcJ7N+/X3rxsVaZcrYk5hYGAlOnTpXf6t/+9jej3A2ccFpPyxs3bmxURZhkrLW9CJ6OMpCAXQKNGjVSaWlpdrPxNH2ghBNPyNHTDMp8WE9bQgKF/fTTT7Lwc6dOnRJIxagkEJsAxgfjdzty5MjYETQ8GhjhxCBtPAjCakcYp8ngLoEpU6ZIY3/vvffcLYi5h4KANUHlxIkTRvgbCOHE015Mo0xNTVVYMo7BGwJ169ZVvCXiDeugl/LBBx/IHzFWMzMhGC+cp06dksHt6Oq/9tprJjAPjI0LFy6Uxj5jxozA+ERH/CPQp08faU+7d+/2z4g4SzZeODGNEqKJWUAM3hNo06aNqlKlivcFs8TAEYBg4rfcrl077X0zWjibN28uoDGjhcEfAh9++KHUwfPPP++PASw1UASeeOIJaU9r1qzR2i9jhfOee+4RwPXr19cacBiM69mzpypUqJAyebWbMNSTCT4ePnxYFS9eXOH+uc7BSOHEsAV06StUqKAz29DY9sUXX0h9RG5PEhrn6ajjBLBHGH7fOk+VNk4433rrLdn2Attf4N+JQQ8C1hjaHTt26GEQrTCaQO3atVWpUqW09cEo4fz8889lm1FstKb7PRBta9wlw44ePSpjaO+++26XSmC2YSIwZ84c6XWOGzdOS7eNEc7z58/LbBV04SdNmqQlzLAblZGRIY2df2phbwnO+H/TTTdJe9JxGUNjhLNWrVoCsX///s7UCnNxhcBVV12lbrjhBlfyZqbhIrBy5Ur5zT/yyCPaOW6EcLZu3VoAcsMw7dpPNoOsS6y5c+dmO8cDJJAogW7duslvf9++fYkmdTW+9sJ5//33CzjcLGYwgwDG19aoUcMMY2ml1gQ2b94sv/8uXbpoZafWwjl+/HiBVrZsWa2g0ZjcCaxatUrqbeLEiblH5FkSiIPAwIEDpT199NFHccT2Joq2wrl8+XKFp+cYWI3FcxnMInDnnXfKQGZTVrsxi2yP7l4AAAj3SURBVG64rD1w4IDoANbt1CVoKZwAhXGaKSkpaunSpbqwoh0JEMDmeBgBgSl0DCRgl8Bzzz0n7entt9+2m5Uj6bUUTswIwo9u7NixjjjJTPwhYO1n/+WXX/pjAEsNDAEMSapatao2swW1E8569eqJaPbu3TswlR5WR7799ltZJ5V1GdYW4KzfWDZSl3HcWgmntQo0xwE62+D8zO3ZZ5+Vxq7TjX0/ebBsewSaNGkiu6zay8V+am2E07qsM3GrUPvVENwcfv31V1WxYkXVtm3b4DpJzzwjsGTJEvkjHjp0qGdlxipIC+F8+eWXBUbJkiVj2chjhhPA1q+4xFq8eLHhntB8HQhg/V20J9wK8iv4Lpxr165V+fLlk3thWMSDIZgEGjZsqHD/moEE7BLAbR8IZ/fu3e1mlXR6X4XzyJEjqlixYrI75bx585J2ggn1J7Bs2TJp7FOnTtXfWFqoPQFs6gbx3LRpky+2+iqc2P8czo8YMcIX51motwQ6dOigypcvr86dO+dtwSwtcAT27t0r47xbtGjhi2++Cef1118voolJ/AzhILBhwwapc6zgz0ACdgk8/fTT0p5wNeN18EU477jjDnG4adOmXvvL8nwmgEVbMJUWs8MYSMAOgWPHjskVTLVq1exkk1Raz4XT2mLhiiuuSMpgJjKbAJYHw+0Zrqtqdj3qYv3kyZOlPU2bNs1TkzwVzhkzZsiDIDwQworuDOEkMHz4cGnsft3YDyf14Hp97bXXypY6XnromXB++umnMuQIQ482btzopY8sSzMCp0+fVqVLl1adO3fWzDKaYyIBjMjx+iGzJ8J56tQpVaJECXFu+vTpJtYNbXaYwEsvvSTtYcWKFQ7nzOzCSODmm2+W9oRNA70Inggn9qHBP4Lf06S8AMoy4idwzTXXKMw9ZiABuwRWr14tGtOnTx+7WcWV3nXhxDYKEE1elsVVH6GKtGDBAmkbM2fODJXfdNYdAvfee6+0p507d7pTQESurgqn5UiDBg0iiuRHEviDADbi4wiLP3jwU/IEtm3bJsLZpk2b5DOJM6VrwolBzuhpYmUcBhLIicD69eulnYwbNy6nKDxOAnETGDJkiLSnf/zjH3GnSSaiK8I5f/58mQ516aWXKu45k0y1hCsNrkwKFy6sfvjhh3A5Tm8dJ3Dw4EF12WWXKbd3xXVcOLHCUcGCBWV2yLp16xwHY2qGjz76qMKLITuB3bt3Sy9h8ODB2U/ySDYCP/74o7QlTGFlyE4AVy+42p01a1b2kw4dcVQ4Mai9TJkyYjSGmzD8QaBmzZqqZ8+efxzgpywEHnvsMWk3XtzYz1KwgV/QM4cwcGhf7MqDDmEkD3qebgXbwvnNN98oDEDFupq1atWSCk1PT3fLXmPzpXDmXnVYYjAtLU3dcsst0lPYvHlz7glCfJbCeeHKx58K/lz69u0r+uT02gi2hBNdYRgX+WrXrt2FvQphDArnhSvdGrpmtadBgwZdOFEIY1A446t0TO222hLeneyh2xJObHURaRg+Y+UjbJXAV1YG5cqVU40bNyaXHNqGtURYdHvCvuxsS1nb0sSJE+V3h1s/ZJOVjcWja9eu2bQJQupUSFo4cS8qupHze9beN3mQB9uAXm1gy5Ytjmhn0sKJ3QuLFCmSTTyxm2FGRgZfUQzw0Kx+/frkEsXFaiu4Lx5LZAYMGEBmUcxGjx4trNCrsvjxPavmtG/fPlt7KlCggDp79qy/wonSrYUarAaPDbmwoAdDdgK8x5mdSfQRLHJstSW833fffdFR+F0pGe8KPk7eswsaWAgkbo1FtqdJkyY55mbSPU7Lgu3bt6spU6aohQsXWof4HoMAhTMGlBiHMDpjwoQJas2aNTHO8hAI8OFQ/O1g0aJFCtuPYzqmk8G2cDppTJDzonAGuXa99Y3C6S3vWKVROGNRceFYjx49OADeBa5hzBLTmNGeMM+fwR8CjgknxnS2bNlSebWQqD+4WKobBDA1F20nt3GbvXr1kjhLlixxwwTmGUACuKeJdoVX79691ahRo5RT08AdEU6IZdGiReVGrFOGBbAe6VIOBLCSFmYN5bRHduREC7avHCDycDYCaE94oX3hVadOHdEofLYbHBFOGAID8QSLPQK7VRK+9FYDR/uJFbA0YceOHaV9xTrPYyQQiwDaU/STdFy5oJNnN8RuqQnkiu1eYQh6AlB0J9Q8geIZNQAErAYeSzjR8CGcuIyHwDKQQDwEMNAd7Sn6CgX6FKudxZNnZBzbwgkFtxo03nO7TxVZMD+TAAhYDdzabz2yoVu3gHCMbYvtJREC1u2dyDRoT3Xr1lXQLLvBlnBGN/ZIEbVrGNOHgwAaOO5vIqBnGSmc1i0gnEMvAXEZSCAeAtCiSpUqyQMhPBTq1KlT5pWLEw+wbQknegFWbxPOoKFD0RlIIF4CkX+2aEvWrR7rFhB6pBBTCKdT84zjtY3xzCWA24ZWe8JVML5DSCP/mO14l7RwWo0ZxliP/PHZifsHdhxiWrMIRN4Xh4hawonPeCHgPifblVn16re1sa5Q0LbwPMbXHmekosMgvNDQYbAThvkNnuV7QwDtxeoFoA2hl4CeJS7f0etEQLuKvLLxxjKWYioBq1NntR/LD+u41d6s48m8J9XjtG68Rhtm3eh3wrBknGEaswhYDdn6o8VQNgikdYlleYN7nxBVBhKIhwDainXfPDK+deVitbfIc4l+Tko40ZCty6joAtGD4FjOaCr8HouANdTIOmcJKRq91bjxzjZlEeJ7PAQw5jfyCgVtaPbs2XKZnpNuxZNvZJyEhdNS8+jeppUpGj17BxYNvudGAA08siFbIglBtYIlpjm1Nyse30nAIoCOHf5sI19O61LCwonL8dyebuIcG7lVhXzPjUCsthJ9mwdtKfpYbnnyHAmgvUS+3CCSsHC6YQTzJAESIAGTCFA4Taot2koCJKAFAQqnFtVAI0iABEwiQOE0qbZoKwmQgBYEKJxaVAONIAESMIkAhdOk2qKtJEACWhCgcGpRDTSCBEjAJAIUTpNqi7aSAAloQYDCqUU10AgSIAGTCPw/V3crN1C4AZ0AAAAASUVORK5CYII=[/img][br][br]Convince yourself triangle [math]ABC[/math] is a dilation of triangle [math]AMN[/math]. What is the center of the dilation? What is the scale factor?
Convince your partner that triangle [math]ABC[/math] is a dilation of triangle [math]AMN[/math], with the center and scale factor you found.[br]
With your partner, check the definition of dilation on your reference chart and make sure both of you could convince a skeptic that [math]ABC[/math] definitely fits the definition of dilation.[br]
Convince your partner that segment [math]BC[/math] is twice as long as segment [math]MN[/math].[br]
Prove that [math]BC=2MN[/math]. Convince a skeptic.[br]
[size=150]Here’s a triangle [math]ABC[/math]. [math]M[/math] is [math]\frac{2}{3}[/math] of the way from [math]A[/math] to [math]B[/math]. [math]N[/math] is [math]\frac{2}{3}[/math] of the way from [math]A[/math] to [math]C[/math].[/size][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUsAAAEMCAYAAABN6pRKAAAgAElEQVR4Ae2dB5QVRRaGJQuSGbIwuEhGQHKUIUmSnHMWYUkOYZag5CwCoghIzuASFgUkRxEWESSLiyAsIkOSKChQe/5ae3gz8ya89zpUd//3nDnzXr/uqlvf7f67uru67guCRgIkQAIkECeBF+JcgyuQAAmQAAkIiiV3AhIgARKIBwGKZTwgcRUSIAESoFhyHyABEiCBeBCgWMYDElchARIgAYol9wESIAESiAcBimU8IHEVEiABEqBYch8gARIggXgQoFjGAxJXIQESIAGKJfcBEiABEogHAYplPCBxFRIgARLQVSyHDx8uRowYEfG3fv16EraAwLp162QMdu3a5bX227dvR8QIn2kk4CYC0KmYjo3YOOgmlqj8hRdeEJUrV474w/dixYoJHpCxhUD/34oWLSpjgZ3Cm2E5YpMmTRpvP3MZCTiWwIIFCyJ0ytdG6iaWU6dOjXbwHT16VDoGB2nmEdBOWh06dIhW6YULF2RMIKg4sdFIwC0E0GnLlSuXCA4O9mvf100sGzRo4NUBHLgx9XDcEiQz26n18MHcmxhCQPEHsWRczIwM67KaAPZ3CCVuU0GXfDXft4ihBjgR9eDTnEJvhmYOAfTwEQuIJs6inqb19LXeJeJDIwE3EECvMm3atAJXuVqHwtd26yKWcARK3bBhw4gHBx07dpSX5bwE9zUkga2PXiN6+ZowepaGniZOaNrOwpOYJx1+djKBvn37yk4E2qh1FnAc+GK6iKV28EV9uDNt2jRffOG6OhDw7OHjBKYJImKEBzo4sUEw+XBHB9gswhYENHH0vJLCsWGJWGr3AjzJoWeDAxKXhTRzCGg9fG0nAH/tM+5RarGI6f6yOV6yFhIwlwCutiCOISEhEX/4HvW2YVxe6dKzRI8SB2BU03qaUZfzuzEEIIzYCTQDf9wGwR96nJp59j61ZfxPAk4koB0TuAyHOGp/OAawzBd7fmT5slWUdWPqQfrjUJSi+dUHAtgR0IPUDCcwLEMctHvH2iWJ1uPU1uV/EnAigZg6bP5cXQUslt4OPlwO4gEPejm4HKeZQwA7AC45NINQ4gkgdhjNtBEKiBGNBJxMQOtVeusY4NjACzO+WMBiqR182v0ADFeBSKI343lD1RenuK5/BNDD13qQKAH3KBELz51F62n6VwO3IgH7EIAGeXYePD3Xjg3PZXF9Dlgs0bPEwRj1L66K+bv+BBADzx4jPnsKJWpET5+9ff3Zs0S1CGj7vufx4Omh9rvnsrg+ByyWcVXA30mABEjACQQolk6IIttAAiRgOAFdxXL06NGiQoUKokWLFmLHjh2GO88KYiewdetW0bx5c1GxYkUxduzY2FfmryTgYAK7d+8WLVu2lPo0cuRIv1qqm1i2b99ePkzAAwXt7+DBg345xY0CJ7Bv376IOGjx6Ny5c+AFswQSsBmBb7/9Ntqx0Lp1a59boYtYhoeHR3MGB2iZMmUi3hX3nBSYn59PkGwUi5IlS3qNSVhYGGPiMUG1UfxZrvH7eHwZlytXzuuxcOXKFZ8EUxex/Omnn7w6kyVLlojXi7ShRfz//JUrI1lkzpzZa0yw4xhZL8s2J77kHH/OWbNm9Xos/PDDD+aLJWosX758NIdWrVrlkzNcWT8Cy5YtixYPz8Hp+tXEkkhAbQJr166NdiyULl3aZ6d16Vmi1rNnz4o333xTOpUwYUKBvzNnzvjsEDfQjwAeuAUFBUXsKBMmTNCvcJZEAjYh0KdPH5E+fXr5h9uD1atXF6dOnfLZe93EUqv5/v37Yvny5fIA7dKli7aY/y0k8ODBA1GjRg2RO3duC71g1SRgPoGJEyeKZMmSiX/961+ycuiTv6a7WGqOlChRQgrm3r17tUX8byEBDJ3AWZW9SwuDwKpNJbB06VK5z8+aNUuXeg0TS7xmh4Ozfv36ujjKQgIn0KZNG5EqVSpx48aNwAtjCSSgMAHoT8qUKcX777+vm5eGiSU8rFevnhRM3GClWU/g9OnTMh6hoaHWO0MPSMAgAnjKnS9fPtG1a1ddazBULOE0epcYrkJTg8C7774rYwLhpJGA0wjgnmTVqlVFnTp1RCD3J71xMVQsUeHbb78tD87Zs2d7q5/LTCaAS3Bcirdt29bkmlkdCRhPAPs15qk8d+6c7pUZLpb37t2TYvnqq6+Kx48f694AFug7gfHjx8uY4KEPjQScQgBvp2XKlEkYtV8bLpYIBF5LwuX4mDFjnBIX27cDw4gwnIhGAk4g8NFHH0mNwbBFo8wUsYTzuPTDTN6XL182qi0s1wcC8+fPlzvX6tWrfdiKq5KAegTWrFkj9+UpU6YY6pxpYjlnzhzZIF8zqhnaepcXjgdvngnOXI6DzbchAcxsljFjRtG/f3/DvTdNLNESPM7H5TjTGhge13hV8OWXX8p4fPzxx/FanyuRgEoEcJWKhzmtWrUyxS1TxfKLL76QB6c/c8mZQsOFlSAjJGZl4cM3Fwbfxk1++vSpqFu3rsxceu3aNVNaYqpYokWYWgq9S8ziTbOewL///W8ZDz3fdLC+VfTA6QQwJDFPnjymXqWaLpZHjhyRByefxKqzO3fr1k0kSpSID9/UCQk9iYUA0kKkSJFCbNy4MZa19P/JdLFEE3AZjt4l5lykWU/g4sWLMh7vvPOO9c7QAxKIhcDcuXPlvvrZZ5/FspYxP1kilr/88otsMG7O0tQgMHToUBkT9PxpJKAigc2bN8t9dNSoUZa4Z4lYoqUDBgyQDZ82bZolDWelkQk8fPhQvv3QuHHjyD/wGwkoQOD48eMiODhYWHn1Y5lYgj9mU8+ePbu4e/euAuGgC9OnT5cnMJzBaSSgCoGbN2/KtDWY7vHRo0eWuWWpWGLEPe5d4hKQpgaBwoULyzzjanhDL0hAiGbNmglkK0ViRCvNUrFEw7NlyyaSJk0qfvzxRys5sO6/CKxYsUKewBYtWkQmJGA5gX79+kmN2L9/v+W+WC6W2sGJcVM0NQhUq1ZN5M2bVw1n6IVrCUyePFmeuFWZv8ByscSegC42LscPHDjg2h1DpYbv2LFDxmPSpEkquUVfXERAS3qo0gNgJcRSS6bVqFEjF+0OajcV79umTZtW3L59W21H6Z3jCEAPUqdOLQYNGqRU25QQSxDBky70LrWUlUpRcqEzJ06ckPHAEC8aCZhFAM8uChQoINq1a2dWlfGuRxmxxDTwEMuKFSvG23muaCwBTKeHmCCXEo0EjCaA/Pa4X44/DBdSzZQRS4Dp3r27PDjxShPNegKYzQXv4LZv3956Z+iB4wlgP0OvElc1KppSYolsbOjJYN5LmhoExo4dK2Oyb98+NRyiF44kMHjwYJlNYcuWLcq2TymxBCXMKALBRFItmhoEcuXKJWrVqqWGM/TCcQQw+TSO+QULFijdNuXEErSQqyd9+vQiPDxcaXhucQ4zvGBnRq4TGgnoSWDdunVy38IVjOqmpFhq+XpCQ0NV5+ca/0qXLi2KFy/umvayocYTwMTTmTNnFn//+9+Nr0yHGpQUS7Qrf/788oyD2UZo1hPAkC70Lj/99FPrnaEHtifw3//+V558McvVkydPbNEeZcVSS6al4ngrW0TWACffeust8fLLL9tm5zYAAYvUgcCzZ89EvXr1RNmyZcWlS5d0KNGcIpQVSzS/SpUqsjeD1+9o1hP45ptvZDzwEI5GAv4SwJyUOOkija2dTGmx/O677+TBySex6uxSnTt3lrNEYbZ7Ggn4SmD06NHymF67dq2vm1q+vtJiCTpt2rSRcFeuXGk5LDogxPnz52U87HJTnjFTh8D8+fPlvmPXPPXKi+XVq1cl4BIlSqgTdZd78o9//EPG5NixYy4nwebHlwAGmydJkkQMGTIkvpsot57yYgliAwcOlAfnjBkzlAPoRofu3bsngoKC5AzWbmw/2+wbgZMnT4pXXnlFdOzY0bcNFVvbFmIJZokTJxY5c+bkk1hFdqAPP/xQnsBUfj1NEVSudgMTYmBynJo1a4o7d+7YmoVtxFI7ON9//31bA3eS8wULFhSVK1d2UpPYFp0JtGjRQiCv05kzZ3Qu2fzibCOWQJMjRw45C46dxmaZH1Lzaly6dKnsXS5ZssS8SlmTbQjgDTy8uuyUoX+2Eks8EcdbJD169LDNDuN0R0NCQuS0Wk5vJ9vnGwEtc6uTTqS2EkuEq1SpUlIwDx065Fv0uLYhBLZu3SrjgYODRgIgoCUhnDhxoqOA2E4s9+zZIw/Opk2bOioQdm5M8+bNRYYMGcTdu3ft3Az6rgOBvXv3ytxNmGXfaWY7sUQAGjRoIAUT74/TrCeA8Za4PRIWFma9M/TAMgL/+c9/BB76NWvWzDIfjKzYlmKJpEY4OPkk1shdw7eye/XqJWOCA4bmPgIPHz4UNWrUkMOEnPoqrC3FErsiXsaHYKo+u7JbDhscIMmSJROdOnVyS5PZTg8CGHAeHBwsvv32W4+lzvpoW7HU8vUUKlTIWRGxcWtGjRolT2AHDhywcSvouq8Ehg4dKhImTCg2bNjg66a2Wt+2YgnK2sE5adIkW0F3qrOYxBVjYevWrevUJrJdUQjMnDlTniBnzZoV5RfnfbW1WCIc6dKlE5kyZRLoadKsJ4CDBrdH1q9fb70z9MBQAtrs+W55q872Yqkl08JkGzQ1CGCGKIyHpTmXAO5NZs2aVXTt2tW5jYzSMtuLJdqD4QoJEiQQeEpOs54AJnZF7xKJ52jOI3DlyhVRsmRJUadOHVdd0TlCLDdu3CgPTrtPAeWkw6p27dry6aiT2sS2/J8AxjkXLVrUdZ0TR4glQli1alUpmHjDh2Y9gf3798t4jBkzxnpn6IFuBHr27CnSp08v3HicOUYsjx49Kg9OZCCkqUGgQ4cOInny5OLatWtqOEQvAiIwduxYeYzh3W83mmPEEsFr27atDObnn3/uxlgq1+Zz587JePTp00c53+iQbwQWLlwoY+nmCVMcJZa//vqrDGiZMmV82xO4tmEEtJQgx48fN6wOFmwsgW3btokXX3xR9O/f39iKFC/dUWIJ1trBicGyNOsJ/Pbbb3IsbMuWLa13hh74TAD5c3Lnzi1atWrl87ZO28BxYokAJU2aVPztb39zWqxs257JkyfLHv/27dtt2wY3On7r1i3xxhtvyD/edxbCkWI5depUeXCOHDnSjfu4km3Oly+fHLGgpHN0yisB9CaRlREPT2kOFUsEFjOgpEqVSty4cYNxVoDAokWL5Als+fLlCnhDF+IiMGDAAJlRddOmTXGt6prfHdmzRPRWrVolD87evXu7JpiqN7RSpUqCs0SpHiUhtEyqc+fOVd9ZEz10rFiCIZ6K47W7EydOmIiUVcVEYPPmzTIe06ZNi2kVLreYgNbJwIxetMgEHC2WyAcCseST2MhBt/JbkyZNRMaMGcWDBw+sdIN1eyGwb98+OXIBE2vTohNwtFiiuVq+ni1btkRvPZeYTuDIkSPyBDZkyBDT62aFMRM4f/68KFy4sKhfv7549OhRzCu6+BfHiyVywqB3Wa1aNReHWa2mI+87YnLhwgW1HHOpN7///ruoWbOmeP3118VPP/3kUgpxN9vxYgkE2sG5ePHiuIlwDcMJXL58WT5pddNciIZDDaCCzp07i6CgIIHJT2gxE3CFWOL+GHoyRYoUiZkEfzGVwPDhw2VMDh06ZGq9rCwygffee0/GgfMpRObi7ZsrxBINHz16tNwpMCyCZj2BP/74Q2TLlk3eI7PeG3d6oKUAmT59ujsB+Nhq14gluGTIkEFOhf/s2TMfMXF1Iwh88skn8gT2xRdfGFE8y4yFAJjjaissLCyWtfiTJwFXiSUG2WIHGTx4sCcDfraQQLFixUTZsmUt9MB9VSN/Tvbs2UW7du3c1/gAWuwqsQQnDI9InDixQB4RmvUEcK8MJ7B58+ZZ74wLPPjll19E6dKlRZUqVcTNmzdd0GL9mug6scS7rjg4+SRWv50o0JLefPNNzhIVKMR4bt+oUSPx6quv8q22ePLyXM11YonGV69eXQrm4cOHPVnws0UEkM8FJ7Dx48db5IE7qu3Vq5dIliyZ4Asa/sXblWKp5evB2z00NQggJUjKlCnF9evX1XDIYV7gRIQTEtJD0Pwj4EqxBCrc3MbOs2HDBv/IcStdCZw5c0bGo1+/frqWy8KEwMsY2NfHjRtHHAEQcK1YYuZn7EDly5cPAB831ZNAaGiojMmpU6f0LNbVZSF/TooUKQQuwWmBEXCtWALboEGD5ME5Z86cwChya10I4Ols6tSpRevWrXUpz+2F4KSTJ08egYc6T548cTuOgNvvarEEPWStww5FU4PAhAkT5Als165dajhkUy9u374tQkJCRMmSJcWlS5ds2gq13Ha9WGIiWlyOI4E8TQ0CGNqCEQs0/wmgd545c2Zx8OBB/wvhlpEIuF4sQQNJmdKmTSswVRXNegLz58+XJzDM2k3znYCWDnrt2rW+b8wtYiRAsfTI18MnsTHuJ6b/gAdvnCXKd+zalRLeu6fpS4Bi+RfPcuXKyd4MZoymWU/gyy+/lPGYMWOG9c7YxAPt1dGhQ4faxGN7uUmx/CteyD+Ce5dt2rSxVwQd7G3Dhg1FlixZmOYgHjHGxL2YVatjx47xWJur+EOAYulBrXHjxlIwOWO0BxQLP+J1VJzAMEEtLWYCSAWBWxZInXLnzp2YV+QvARGgWHrgwyU4Dk5M7EBTg8Dbb78tEiZMyOEvMYQDycVq164t8ubNK/AWFM04AhTLKGx79uwpBXP16tVRfuFXKwj8/PPPIkGCBKJ79+5WVK98nZg9K3ny5GLHjh3K+2p3BymWUSL48OFDKZbIdEdTg8CwYcNkTDBpLe05AS2P0ZIlS54v5CfDCFAsvaAdM2aMPDiZm8QLHAsWYfwrBljjtT3a/wngFV3cMpo0aRKRmESAYhkD6IwZM4qXX345hl+52GwCH330kRQHTN7sdtPy53BcsLl7AsUyBt5Ic4AzNy4BaWoQeO2110SFChXUcMYiL44cOSJy5MghmjRpYpEH7q2WYhlL7DEcAzNLY1ICmvUEVq5cKU9gbp3A9urVqzK5G3LoIJcOzVwCFMtYeG/evFkenHwSGwskk3/CWEK3zhKF3mTWrFkFH3SZvNP9VR3FMg7uGHOJy3FOSBsHKJN+3rlzp4yH2x5s9OnTR7abM/ubtKN5qYZi6QWK56Jjx47JnRRv99DUINCqVSuRJk0acevWLTUcMtiLiRMnyn1w1qxZBtfE4mMjQLGMjc5fv3Xo0EHurNu3b4/H2lzFaAInT56U8ejfv7/RVVlePsZQ4soGYypp1hKgWMaDf3h4uNxhK1WqFI+1uYoZBPr27StjcvbsWTOqs6QOnJyR8bJLly6W1M9KIxOgWEbmEeO3sLAweXAiUx7NegI4gb300ksyS6f13ujvwenTp0W+fPnkPAUPHjzQvwKW6DMBiqUPyJAlL3/+/D5swVWNJIDUrrhE3bt3r5HVmF72b7/9JqpUqSIKFCggfvzxR9PrZ4XeCVAsvXPxuhSvP+LgxA13mhoEkBKkZs2aajijkxdt27aVl9979uzRqUQWowcBiqWPFHPnzi0nWfVxM65uEIG5c+fKE9g///lPg2owt1jtds+KFSvMrZi1xUmAYhknosgrYOo29C7d8CQ2csvV/VamTBnhhFmitPffp0yZoi5sF3tGsfQj+Hg/GYKJ189o1hPAQG3EY+bMmdY746cHWv6c0NBQP0vgZkYToFj6QRhpJ3Bwtm/f3o+tuYkRBOrVqyeyZ88u/vzzTyOKN7TMr7/+WmCWq2bNmhlaDwsPjADF0k9+TZs2lYL53Xff+VkCN9OTwMGDB2U8RowYoWexhpd14cIFUaxYMYHsohgORVOXAMXSz9ggSRR6l8h/QlODAAZvJ0mSRFy5ckUNh+Lw4vHjx6Ju3bpy3lS8VktTmwDFMoD49OrVSwomclzTrCegncCQR8kOhmRsOOFyQmM7REsIimUAcUK6A+zsJUuWDKAUbqongcGDB8uYHD16VM9idS9r5MiR0k8MfaLZgwDFMsA4afl6PvvsswBL4uZ6ELh//74ICgoSuKesqmn5c0aNGqWqi/TLCwGKpRcovi5CMq3g4GBfN+P6BhGYOnWq7LVt2bLFoBr8Lxa3bBInTiy6devmfyHc0hICFEsdsM+fP18enLi0oqlBoGDBguKNN95Qw5m/vMDICZxUa9WqJfBwh2YvAhRLneKF4R+YBYcHgU5AAyxm2bJl8gSmSk7tX3/9VZQvX14UKlRIYLgQzX4EKJY6xeyrr76SB6ddnsTq1GyliwkJCVFmligMOE+dOrXAAHSaPQlQLHWMGy6v8HT84sWLOpbKovwlsG3bNhmPDz74wN8idNkO+b2xX+CVRpp9CVAsdYzd999/Lw8KvramI9QAi2rRooVIly6duHPnToAl+bc5EqtBKDG9H83eBCiWOsevU6dO8uA4cOCAziWzOH8IaCewQYMG+bN5QNto+XMGDhwYUDncWA0CFEud43D9+nUplrhfRlODQO/evWVMzJx1fMeOHfIeZcuWLdWAQC8CJkCxDBhh9AK0t0jWrFkT/UcuMZ0AptJ78cUXRceOHU2p+8yZM/LBEqbyc0u6XlPAWlwJxdKgACArX+HChQ0qncX6SmD06NGyd2n002jcG61WrZrImTOnQMpemnMIUCwNiqU26/WMGTMMqoHF+kLg6dOnUsDq1Knjy2Y+r4s5ThMkSCC2bt3q87bcQG0CFEsD45MnTx6BVyFpahCYPXu27F2uW7fOEIe02y8LFy40pHwWai0BiqWB/LVUATiIaGoQwAxRRswSpV1JjB07Vo2G0gvdCVAsdUcaucBKlSqJhAkTirt370b+gd8sIYBeJcY9opeplyGzJMp855139CqS5ShIgGJpcFDwQAEHEsZf0tQggPuWeADz7NmzgB3CeFrcasGM50+ePAm4PBagLgGKpQmxad68uRTMs2fPmlAbq4iLgHYCwxPyQAyvtRYvXlwUKVJEXL58OZCiuK0NCFAsTQiSlu4AGQhpahDAmEuMvcRsQP4YZpdCPPEq5aFDh/wpgtvYjADF0qSA9enTR/Yud+7caVKNrCY2AnibB7dH8HaPP4b7k9jeqCfr/vjEbYwlQLE0lm9E6Y8ePZLj78qWLRuxjB+sJYD3xSF4x48f98kRpIPAdh9//LFP23FlexOgWJoYv3HjxsmDDBPT0qwngLdtcBmNmYnia8i1BKEMCwuL7yZczyEEKJYmBzJr1qwid+7cJtfK6mIigLkuIX7bt2+PaZWI5Rs3bhRJkyYVrVu3jljGD+4hQLE0OdYLFiyQB+fkyZNNrpnVxUQgf/78okqVKjH9LJcjte4rr7wiMG7WqrkxY3WQPxpOgGJpOOLoFWC4CVIM0NQgsHjx4lhvj1y7dk1UrFhRiiWHf6kRMyu8oFhaQB0pWnHpFxoaakHtrNIbAWSCREZIb4Z7mkhfy5EM3ui4ZxnF0qJY4y0SCGZ4eLhFHrBaTwJawjnkHPe0d999V8Zp6dKlnov52YUEKJYWBR3DVSCWrVq1ssgDVhuVQNOmTUVQUJBYv369wGuMWv6c8ePHR12V311IgGJpYdC7dOkiBfPYsWMWesGqNQKffvqpjAdOYtpf9+7dtZ/53+UEKJYW7gA3btyQB2X16tUt9IJVawRef/31CJHUxHLIkCHaz/zvcgIUS4t3gKFDh8oDdPPmzRZ74u7qtURzmkhq//Hgh0YCIECxVGA/wDCiokWLKuCJu13Inj17tJ4l56h09z7h2XqKpScNiz7jHWP0ZObNm2eRB6wWBMqVKxdJLDFPJTI10kgABCiWiuwH+fLlE9myZVPEG/e5gXuTOGHhnW/Mc4k0ERzW5b79ILYWUyxjo2Pib1pqgjFjxphYK6sCAWTghFDyYQ73h9gIUCxjo2Pyb5UrVxZJkiRhegITua9Zs0YKZbt27UyslVXZkQDFUqGoYSA0ejg9e/ZUyCvnuvLNN98IzAIVEhIiHjx4IIYPHy4w0Yk3w3JO9OuNjHuWUSwVi3XLli2lYF66dEkxz5zlzs8//yxT4mK6PMyafvv2bck9bdq08nPU1gYHB0sxjbqc391DgGKpWKwvXLggD9pGjRop5plz3Pnjjz9EgwYN5NyUe/bskQ1DrzFNmjTyL2rvUhPSXbt2OQcCW+IzAYqlz8iM36Bfv35SMJkIyxjWPXr0kHyXL18eUQEuwXHPuEOHDvKyPOIHIeTlN26P0NxNgHuAgvFH5sBEiRKJChUqKOidvV3S8udMnDgxUkMglH379hWY5BfCiB6+ZhBSvjSg0XDvf4qlorGfMGGCPGj5UEG/AM2dO1cy9ZbREZfg2uV31PuTWo9TP09Ykh0JUCwVjhpev8ubN6/CHtrHtU2bNsk84Q0bNozmtHafGL1KGOa0zJUrV8R6nkIasZAfXEeAYqlwyBctWiR7QjNnzlTYS/VdwxR4eOpdokQJr2/loEfpeU9SE0880NEuyzUhVb+19NAoAhRLo8jqVG7JkiVluladinNdMcifg5mDMmXKJGKaNxT3KnGp7Wl4Wo6HPVGF1HMdfnYXAYql4vHW8vUMGzZMcU/VdE8bt4rL8JgMQomHOJ4GkcSYS29C6rkeP7uHAMXSBrF+66235GXi/fv3beCtOi5q+XNmz54dq1O4BPf2IA33KjXBjLUA/ugKAhRLG4T5xIkTUiw7d+5sA2/VcBF52SGCcfXItXuSnkOFtBbgMjwmIdXW4X/3EKBY2iTW3bp1kwcuXs2jxU5g2bJlkhXELi7D2zkxvZmj/Yb/NBKgWNpkH7h586YUgNq1a9vEY2vchPClS5dOVK1aVWBwP40E9CJAsdSLpAnlvPfee1IwtfeZTajSVlX88MMPonDhwiJPnjyR3sCxVSPorLIEKJbKhsa7Y3jgULx4ce8/unjp3bt3Rc2aNTOHQrAAAAjnSURBVEXy5MnF119/7WISbLpRBCiWRpE1qFwMUMdDhxUrVhhUgz2L7dSpk+SyatUqezaAXitPgGKpfIiiO1igQAGRI0eO6D+4dImWP+eDDz5wKQE22wwCFEszKOtcx9q1a2Uv6sMPP9S5ZPsVp2XGxOBxGgkYSYBiaSRdA8uuUqWKnBjCwCqUL1o7aTRu3Fh5X+mg/QlQLG0aQ+SPwb3LAQMG2LQFgbl98OBBgVmZSpUqJW7duhVYYdyaBOJBgGIZD0iqrtK6dWspmDdu3FDVRUP8Qv6c0qVLiyxZsoiTJ08aUgcLJYGoBCiWUYnY6PvFixelWLZp08ZGXgfm6p9//ikwJyV61ZhkhEYCZhGgWJpF2qB6QkNDpXDg/XE3mJY/B7Oe00jATAIUSzNpG1AXMhUmSZJE4IGP02306NHyxBB1OjWnt5vtU4MAxVKNOATkhTbDjpMvS+fNmyeFkjMvBbSrcOMACFAsA4Cn0qYYpI7B6k60zZs3ixQpUogaNWqIp0+fOrGJbJMNCFAsbRCk+Li4ZMkS2fNauHBhfFa3zTpIBYGJMfLnzy8uX75sG7/pqPMIUCwdFFMMpwkKCnJMi8LDw2VunJdeeklgXCWNBKwkQLG0kr7OdW/btk32LseNG6dzydYU16pVK9mezz//3BoHWCsJeBCgWHrAcMLH+vXrS4F59uyZrZujDYni+++2DqOjnKdYOiqcQr7RggHbvXv3tm3LMHsQ2oCEYzQSUIUAxVKVSOjoR/fu3aXYXLlyRcdSzSlq+fLl0vdmzZqZUyFrIYF4EqBYxhOUnVbDxBLomTVp0sRObovdu3eLDBkyiLJlywrMfE4jAZUIUCxVioaOvuAtFwjm4cOHdSzVuKKQP6dIkSJyJqGzZ88aVxFLJgE/CVAs/QRnh83Sp08vypcvr7yr9+7dE7Vq1ZLijif6NBJQkQDFUsWo6OTTrFmzpABt2LBBpxKNKUbLnzN//nxjKmCpJKADAYqlDhBVLqJQoUIiV65cyro4dOhQKegjR45U1kc6RgIgQLF0+H6wfv16KUboZapmn3zyifSta9euqrlGf0ggGgGKZTQkzltQrVo1kTJlSqUatm7dOpEwYUKZ61spx+gMCcRAgGIZAxgnLT506JDswakyDyTe88YsSQULFhRXr151Emq2xcEEKJYODq5n09q2bSsF8/fff/dcbPrnS5cuiTJlyohUqVLZZliT6ZBYoZIEKJZKhkV/p5DkC+Muu3Xrpn/h8SzxyZMnEflzkMaWRgJ2IkCxtFO0AvQVaXMhmOfPnw+wJP8279mzp6x/+vTp/hXArUjAQgIUSwvhm101MiMmS5ZM1K1b1+yqxZgxY6RQujXPuenAWaHuBCiWuiNVu8ApU6ZI0dq/f79pjmKwOXq0LVq0MK1OVkQCehOgWOpN1AblBQcHi+LFi5vi6VdffSWHLeG1y4cPH5pSJyshASMIUCyNoKp4mcuWLZM9vdWrVxvq6ffffy/y5s0rhwmdO3fO0LpYOAkYTYBiaTRhRcvHNGhZsmQxzLvr16+LkJAQKco7d+40rB4WTAJmEaBYmkVasXp27NghhWzatGmGeKblz1m0aJEh5bNQEjCbAMXSbOIK1dewYUORKFEi3T3q37+/FGI8AaeRgFMIUCydEkk/2nH69GkpamFhYX5s7X0T7Wk7UlvQSMBJBCiWToqmH23p0aOHFMzbt2/7sXXkTVasWCHLqlOnTuQf+I0EHECAYumAIAbSBC1fT7t27QIpRubPyZgxo3jttddEeHh4QGVxYxJQkQDFUsWomOwTJt7FoPFTp075VTOGBRUtWlSkTZtWHDlyxK8yuBEJqE6AYql6hEzyLygoSFSvXt3n2u7fvx+RPwcTDdNIwKkEKJZOjayP7ZozZ47sXW7fvt2nLTt37iy3mzFjhk/bcWUSsBsBiqXdImagv7jfiAl542vDhg2TQjlo0KD4bsL1SMC2BCiWtg2d/o4jCyTuXS5evDjOwmfOnCnXxeBzGgm4gQDF0g1R9qGNNWrUEOnSpYt1C+TPSZw4sahUqZJ4/PhxrOvyRxJwCgGKpVMiqVM7Dh8+LHuMEydO9Foi8vnkzJlTpte1ahJhr45xIQkYTIBiaTBgOxbfvn17KZhRfb98+bLABBx4RXL37t1Rf+Z3EnA0AYqlo8PrX+Mgirh32bdv34gCnj59Kho1aiSXL1myJGI5P5CAWwhQLN0SaR/biSfcEMyxY8fKBz7aa5Hjxo3zsSSuTgLOIECxdEYcdW/FwoULpVhCMLW/QF+J1N1JFkgCJhKgWJoI205V5c6dO0IkNbHs06ePnZpAX0lAVwIUS11xOqMwTIShCaTnfwwVopGAWwlQLN0a+TjajTd5PIUSnwcOHBjHVvyZBJxLgGLp3NgG1DIMPEeOcU0wS5UqJW7evBlQmdyYBOxMgGJp5+gZ7Dsux1euXCk2bdpkcE0sngTUJ0CxVD9G9JAESEABAhRLBYJAF0iABNQnQLFUP0aWeojcPBhzOWLECIFskPh/9OhRS31i5SRgBQGKpRXUbVLnggULZKqINGnSiAYNGsjXH5E+onLlyjZpAd0kAf0IUCz1Y+mokvA0HE/CO3ToIPTI/OgoOGyMKwlQLF0Z9tgbDXFE8jH0JmkkQAL/J0Cx5J4QjcDUqVMFLr3Zo4yGhgtcTIBi6eLgx9R03JdkrzImOlzuVgIUS7dGPpZ2417l8OHDY1mDP5GA+whQLN0X81hbfOHCBflgZ9euXbGuxx9JwG0EKJZui3gc7dXEEsOGaCRAAs8JUCyfs+CnvwhoQ4YIhARI4DkBiuVzFvz0FwHcr4RgYqwljQRI4P8EKJbcE6IRwJAhPA2HYBYrVkyEhITI/3xzJxoqLnARAYqli4Lta1PxDjjGXKKnif+4n0kjAbcSoFi6NfJsNwmQgE8EKJY+4eLKJEACbiVAsXRr5NluEiABnwhQLH3CxZVJgATcSoBi6dbIs90kQAI+EaBY+oSLK5MACbiVAMXSrZFnu0mABHwiQLH0CRdXJgEScCuB/wGkO1gucT4wCQAAAABJRU5ErkJggg==[/img][br]What can you say about segment [math]MN[/math], compared to segment [math]BC[/math]? Provide a reason for each of your conjectures.
Dilate triangle DEF using a scale factor of -1 and center F.
How does [math]DF[/math] compare to [math]D'F'[/math]?[br]
Are [math]E[/math], [math]F[/math], and [math]E'[/math] collinear? Explain or show your reasoning.[br]
IM Geo.3.5 Practice: Splitting Triangle Sides with Dilation, Part 1
What is the measure of angle A'B'C?
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAVEAAAE7CAYAAABkGbJ+AAAgAElEQVR4Ae2dB7QTRfvGP6RLlQ6KFBHhj4h0ERBRioL0jlTpTXpTelGkg4ACgjRBQECaSJVeBQQpUqQJIr1LE+Z/nvm+wdzc5GaT7G62PO8599xkMzvlN5snszsz7/sfQSMBEiABEgiZwH9CPpMnkgAJkAAJCIooLwISIAESCIMARTQMeDyVBEiABCiivAZIgARIIAwCFNEw4PFUEiABEqCI8hogARIggTAIUETDgMdTSYAESIAiymuABEiABMIgQBENAx5PJQESIAGKKK8BEiABEgiDAEU0DHg8lQRIgAQoorwGSIAESCAMAoaK6Ndffy369esX5e/kyZNhVJenkgAJkIC1CBgqosmSJRMlSpQQffv2Fe3btxd58uQR//nPf8SiRYusRYG1IQESIIEQCRgmohhxQjB/+umnKFWDkEJYaSRAAiTgBAKGiShGmxDRa9euReHUsGFDimgUInxDAiRgZwKGiShu4TNlyhSFDUanyZMnl7f3UT7gGxIgARKwKQHDRBS37JkzZ34yqVS5cmUpqng2SiMBEiABpxAwTERxK6+ef0JQMSp98803xd69e53Cju0gARIgAWM820MofU0qVapUSY5OyZ0ESIAEnELAkJEo1odCRL1t1KhRPo97p+N7EiABErALgehKp0PN8dzT1zImHMfaURoJkAAJOIWAISKKZ6HeE0hqdIpZexoJkAAJOIWAISKKW3nvP4xAKaBOuWzYDhIgAUVAdxHF4nrsUvL84355hZv/SYAEnEZAdxF1GiC2hwRIgARiIkARjYkOPyMBEiCBAASCFtFdu3aJpk2bijJlyohhw4YFyJ4fkwAJkICzCQQlor/++quIEydOlEkjOBShkQAJkIBbCQQlot26dYsioGoG/ty5c27lx3aTAAm4nEBQIorbeCWcnv+3bdvmcoxsPgmQgFsJBCWi8+fPjyai8ePHl8datmwpTp8+7VaObDcJkIBLCQQlomCEmEmJEyd+IqaYXJowYcKT0B/16tUThw4dcilONpsESMBtBIIWUQUIs/S4pYdnJmXTpk0TRYoUkcfhP3Tnzp3qI/4nARIgAUcSCFlEQaN69epSMNevXx8FDm77S5UqJT/D/3Xr1kX5PNJvsKsKdfYOXRLperF8EiAB+xEIS0R37NghhbJx48Y+W758+XI5UsWIFSPUJUuW+Exn1kHEfXr11VdlndXEGLzv01G0WT3AckjAeQTCElHggMu7WLFiif379/ulg1FfnTp1pHjlzp1bzJ49229aIz/AmlY4QVF7+TESxeMIxH2ikQAJkEAoBMIW0WXLlklx7NSpU8Dy1W4njAKzZMkiJk2aFPAcoxP488JvdLnMnwRIwBkEwhZRYMiZM6dImTKlOHv2rCYqBw8eFB9++KFIkCCBSJ06tYDH+3/++UfTuXonUqGdeUuvN1nmRwLuIKCLiE6dOlWORgcNGhQUtVOnTomePXuKFClSiIQJE4qBAweKmzdvBpVHOInhrg/PSD1XGISTH88lARJwHwFdRBTYUqVKJV588UVx586doClevHhRQIAzZswoxbh79+7i/PnzQeej5QSMOBF1FI8U8CzU2wO/ljyYhgRIgAQUAd1EdMiQIVKYsPA+VIMAjxw5Urz00ksyrzZt2ojff/891Ox8nufpNBqTTCqUM5c7+cTFgyRAAgEI6Caijx49ksJXqFChAEUG/njr1q1i4sSJIl++fDJPzKrHNPsfOEf/KSCeCF2C57I0EiABEgiWgG4iioI7d+4sRe/bb78Nth5P0j9+/Fj06tVL/Pbbb/LYzJkzRfHixWW+1apVE9u3b3+SVq8XWKZFl3560WQ+JOAuArqK6F9//SXF7p133gmZImbLZ8yYEe38hQsXirJlyz7Jf+3atdHShHIAI1E8G2UQvVDo8RwSIAFdRRQ469evL4Vu5cqVQdM9fPiwgM/SW7du+T0X+VatWlWWUaxYsaB2QWEWHvv7sfgff99//72cncdzUT4T9YucH5AACcRAQHcRxbNLzHzXrVs3hmKjf3T79m3Ru3dvsXv37ugf+jiyadMmAY9RKAvLlLQ8QsAte548eeQ5OA+vMTuvdjD5KIaHSIAESCBGArqLKErD7TxECjuUtNq4cePE4sWLtSZ/km7Pnj2iRYsWsrxs2bKJKVOmPPmML0iABEjAaAKGiOiaNWukqLVt21ZT/XGLPX36dE1p/SXCRBS2niZKlEikS5dOjB07VmB0SyMBEiABIwkYIqKoMJYnwXlzoHWeENDJkyfr1sY//vhDzu5jOynK/+STTwQW89NIgARIwAgChononDlz5GgUzzl9GSaPcAsf7gjUV944homiTz/9VMDVHbxMffTRR3z26Q8Wj5MACYRMwDARRY2wjfP555+PNvON8CEQVzP8iz58+FCMGTNG5MqVS4o6HJ/AAQqNBEiABPQgYKiIQrwwwaR2A8FT04IFCwT2xmNCyGz76quvRMGCBWWdmjRpwvAlZncAyyMBBxIwVETBC96ZsARp48aN8pZ61qxZEZ/wwaMG5YSkVq1acs2oA/uWTSIBEjCBgOEiii2cGI02aNBAHDt2LOgmYScRBM/b8MyzUaNG8jN8Pnr0aO8k8hkoopNi8sqXYUlVuXLlZP3Kly8vEM6ERgIkQALBEDBcRG/cuCFFqmTJksHUS6aFv08IMP48DQKKCSMslsejAggtnIh4urWDyzu8R1rk4/mZZ154jSVZNWrUkOVgH/28efO8k/A9CZAACfgkEFWdfCYJ/2Dz5s2lQC1dulRzZhA/5e/TW0QhnBBNpFGmBFftPvLeC4/3nunVeZ7/4T0Ko1uUlz9/fr8jWM9z+JoESMDdBEwRUdzGQ5jghUmrYZ87/pQ4ep6H0aKvkSX2wCvxVKNQdZ6v9Ooz7//79u0TrVu3FrFjx5a+TcePHy/u3r3rncwx78FY/fg4plFsCAmYRMAUEUVbqlSpIoV08+bNAZv29ddfS2fJ6lbceySK92rG3zMziKsK9QFRgHDC0QielyLPYA0bBbp27SqSJk0qnnvuOTFs2DBx5cqVYLOJaHoIJJ4Lqz/w8BZM/Pj44hnRirNwErAJAdNEdMuWLVJEmzVrFiMafMFxG48vP8zXSBQiqj73zAyiCSFVpkQ43CB0cPGHEW769Oll3SBIZ86cUcVY+j+Y4NEHuOAPr8FP/aiAN94HetRh6UayciQQQQKmiSjaWLRoURE3blyBxfb+DF90z1vvYEQUQucpov7KCPU49uIPHTpUvPDCCyJOnDjSbR/c91nZwMPb4TRG6xBOGEag3p9buT2sGwlYjYCpIgr/nfjyYrG9L4MIYsbd0/yJKJw3exvEwUgR9SwPW1ZfeeUV2R7EgtLqws8zDzNee446VXkqTDRGn+DlfXuv0vE/CZBAYAKmiiiqkz17dpE2bVpx4cKFaLXDFx5Ll7DuU/1hoT6O470aoXpOIHlm4mvU5fm5Ea9xW/zaa6/JOmJmH5sKrGLqB8j7cQZ+bJQjarN+dKzChPUgAb0JmC6ikyZNkoKD6KDehpGo9x9uNSGiOK6e4+GYmkBSeWBU5WvUpT43+j/Wlr799tuyDjVr1hQ//vij0UUGzB+36mCiPPljgg0/RnguCmHFCNRbYANmygQkQAJRCJguoig9RYoUImfOnFEq4u+NGk15fq6OKVHFZxBW77WjnueY9XrZsmWiYsWKUrywCwq+AiJliglGm/iDoGKkz9v3SPUIy3UigYiI6ODBg+UXGqPSQKYE0zsdBFSJAmbzIaBIaxVDXWrXri3riN1aiFpqtuH5MkbwngZhBS/OxntS4WsSCJ1ARET0/v370sfn66+/HrDm+LL7E0eMqPAZ/qwqCjt37hTwGAXBL1SokPjyyy/FgwcPArY73ATq8Yb3BByYoS7+mIZbLs8nAbcRiIiIAjImifBl/u6771zBHMu62rVrJ+LHjy99m44YMcJQ4YdIgq/3rbs6ThF1xWXHRppAIGIievbsWfklf++990xopnWKwCL9Hj16iGeeeUbOkA8cOFCcO3dO9wriNh6PODwNo1NMLGFmnkYCJKAPgYiJKKqPsMoYLa1bt06f1tgoF2wfHTBggNxOmjJlSimsR48e1a0FWL2AZ59qqRj+gzWek3JGXjfMzIgERERFFN7t8cWGr1G3Gp4P49Ye62dxq4/wJXqIHCbePJeL4T1v4d16lbHdRhKIqIiiYaVKlZJCqodwGAnKjLwx6ZQ3b17JA5NR8DdAIwESsDaBiIvoypUrpWh06NDB2qRMrN2MGTNEsWLFJJc6deqIVatWmVg6iyIBEgiGQMRFFJXFczo8v8NkE+1fAlioX6ZMGSmmWMAP3wPK5s+fL30QzJ49Wx3ifxIggQgQsISIYiE6no1iooUWnQC2kCp/rNhaivW14KX+3LbCITohHiGByBGwhIii+XB6nDVrVoE48TTfBODQWo1MlYCq/8GEXvGdO4+SAAmEQsAyIjpy5Eg5svr8889DaYdrzkHkUiWcnv8/+eQT1zBgQ0nASgQsI6KA8vTTT4sCBQpYiY/l6oKdT57iqV5jJA+fBOfPn7dcnVkhEnAyAUuJKHbyQBS++eYbJzMPu23Y5aTEE//feecd8fHHH4tUqVLJECZ4jfhQNBIgAeMJWEpEsYsHolC6dGnjW27zEk6fPi3gXCRHjhzirbfekq25deuWwG09tnUiuB6Wje3fv9/mLWX1ScDaBCwlokClPB6tWLHC2uQsUjvl5NpzN9Ljx49lhFP4bEUsqObNm4tt27ZZpMasBgk4i4DlRBSB3zAarVWrlrNIG9gaPA+tUaOGzxImT54snzOD6fvvvy/Wrl3rMx0PkgAJhEbAciKKZlSoUEEK6Y4dO0JrlcvOwi08RPLXX3/123Isylfe7StXriyWLFniNy0/IAES0E7AkiKKYG8QhVatWmlviYtTXr9+XSRIkEATr8WLF4t3331X8sWa02+//dbF5Nh0EgifgCVFFM1CBM2ECROKEydOhN9KF+TQqVMnKYxalzjhtr569erynKJFi4opU6a4gBKbSAL6E7CsiMLjPUajWK5DC0zg+PHjklevXr0CJ/ZIgUcmcEUI1vAgNXbsWAH3fDQSIAFtBCwroqj+iy++KJ599lnx999/a2uNy1MhCB0iqYYSw+ngwYPyccBTTz0lfZsipPXly5ddTpTNJ4HABCwtol988YUcIQ0fPjxwS5hCYFSJESXiy4dqp06dEl26dBFJkiSRP2C9e/eOFqcp1Lx5Hgk4kYClRRTAETojd+7cTmRvSJsQ6x5e8sM1jEL79Okj0qZNK+NBde7cWRw4cCDcbHk+CTiOgOVFtH///nJ0NXXqVMfBN6JBy5cvl7xmzZqlS/b37t0Tn332mfSwFS9ePNGyZUuBMNA0EiCB/xKwvIjieWisWLHkGkd2mjYChQsXlj5HtaXWngoetnBXgEcG9evXZ8wm7eiY0sEELC+iYN+2bVv5xfX07O7gPgm7adOnT5e8jNo6i6B3EGqIabVq1QRGvzQScCsBW4goJjvwhcVOG5o2AtmyZZM7v7SlDi0VQpTA+Qn6Bp6k5s2bF1pGPIsEbEzAFiIKvjVr1pRfVuxmogUmoJxc79q1K3DiMFNgxIsQJRDTN954Q2CkSiMBtxCwjYhCDPAl/eCDD9zSN2G1ExNCCP7XuHHjsPIJ5mT8wMFxDPopf/78Yvz48cGczrQkYEsCthFR0H3zzTdF7NixxW+//WZL2GZX+qOPPpKCdvLkSVOL3rNnj/yxg5jC3+nQoUO5YcLUHmBhZhKwlYiq5TtYDE4LTAAhqCFkXbt2DZzYgBRHjx6Vk4Jx48YVzz//vOjXr5+4cOGCASUxSxKIHAFbiSgwvfLKKzIMBjwX0QITgENmxK66efNm4MQGpTh37pzo3r27fLyAzRMQdez1p5GAEwjYTkRVtEtGt9R2+e3bt0+ORrEXPtJ248YNgc0T8IcAD12tW7cWv/zyS6SrxfJJICwCthNRtBae3PXY2hgWORudjLWcuJ22ij169EiMGDFCOpjB44ZGjRqJTZs2WaV6rAcJBEXAliKKiQp8+eCghBaYAHyHgtdXX30VOLHJKSZOnCheffVVWT+EODFqg4DJzWJxLiJgSxFF/+A5Hxw307QRQGiQfPnyaUscgVTY6//6669LMYUTFfiTpZGAHQjYVkQxQ4/R1dy5c+3AOeJ1BCfwQphlKxu29iJkNuqKJW0zZsywcnVZNxIQthVRLJXBF61cuXLsRo0EXn75ZSlQGpNHNNmaNWvkNl/0ccGCBfnoJqK9wcJjImBbEUWj4MkdX7LVq1fH1EZ+9j8CEyZMkLzsNImzbds2UbduXVnvXLlyyQkpq3QoNjFgUgwjZjzXbd++vVWqxnqYSMDWIgonwRBRxFOnaSOQLl06UadOHW2JLZQK4aCbNWsm+ztz5sxiwIAB4tatWxGrIfwD4NqrVKmS9BXw008/0TVgxHojsgXbWkSBToX/3b9/f2RJ2qR0iA++/IcPH7ZJjaNWE6M/jPiwzjRNmjRyEf+ff/4ZNZHB765duyY3DowaNcrgkpi9HQjYXkTXrVsnRaFdu3Z24B3xOiLsR5w4cYTdeV26dElGgsUOqESJEsn2HDlyxBS+EM9MmTKZUhYLsT4B24soEMNBcNKkScXFixetT9wCNfzwww8Fono6gRciH2D3GjYTYIQNL1+7d+82lDKWi6nnn3v37hXr1683tDxmbm0CjhBRtXynb9++1qZtkdphxAbBgUMQJ9nYsWOl1yi0rXbt2oaJW7JkyaSIYjIJI1K8dyJPJ10bRrbFESIKQIhRz1ss7ZcKJuPwTPHx48faT7JJSgQ1hD9TCFuFChXE0qVLda058oVwYjJJGV7juOcx9Rn/O5uAY0QUQdRwEY8ZM8bZPaZT67Zs2SJ5jRs3TqccrZcN7lDgaR/XBcKYzJ49W5dKIj91O++ZoedtvudxvnY2AceIKLoJkwx58+Z1do/p2LqyZcuK//u//9MxR2tmBT+0iAEF8cNW4UmTJoVV0Tx58ghfj46w3AlCSnMXAUeJaO/eveUXhVsFtV3Eixcvlry+/fZbbSfYPNWGDRtkdFKIKUI/h7pECZs8IJje5k9cvdPxvbMIOEpE4XgYMerffvttZ/WSga3Bs8PixYsbWIL1ssbsff369eUPyAsvvCAGDRok/vnnH80VxVpVCPHo0aOfnKMW32O2nuYuAo4SUXRdy5Yt5QXOWOjaLmRMwkAQ3Lh1FrG6cL3ghxc7uRCTSmvEBIgmJpcQDBB/eM0op9quOaelcpyI/v7771IU4JuSpo0AtlFWqVJFW2IHpkIsKngFS5w4sUiSJImcNPrjjz8CthQ7l7jdMyAmxydwnIiix6pWrSqF1OhF1065OpSTa7ffimIUirWzWPqFqLLYq3/o0CGndDPbYRABR4ooPP/gFhVB2miBCdy+fVuOwiAaNCEePnwohg0bJrJkySKvI3iR2rlzJ9GQgE8CjhRRtBTuyeLHjy9wq0YLTKBbt25SMM6cORM4sYtSIAQN/LDiRxkz8gi1QiMBTwKOFVG1fKdHjx6e7eVrPwROnz4thYK8fAOaOXOmKFSokGQEz/vwwE8jARBwrIiicYhRnz59+qCWr7j5smjSpIl05AKnHjTfBBBepWTJklJMERMK4kpzNwFHiyiiW+I2DBMntMAEMBEHXsOHDw+c2OUpVq1aJRBQD7zgiISRZ917QThaRNGtiFHvhq2Nel3CeO6XNWtWvbJzfD5bt24VNWvWlGIKJzj8wXZ8l0droONFFL4mMVqwYsz1aL1hgQMrV66UvKZNm2aB2tinCoisAF+muNYyZMggsAX5/v379mkAaxoyAceLKJarIEZ9sWLFQobkthOLFi0qI2y6rd16tBebPRA1ANEDsJOpU6dO4sqVK3pkzTwsSsDxIgruHTt2lCMEq8dct8o1ApdxGFHp7YfTKu0zox4I6d2zZ0+5HTRu3LiiRYsW4tSpU2YUzTJMJuAKEUUgM4hCxYoVTcZr3+Jy5MghgwDatwXWqPmdO3fE4MGD5S0+rsF69eoJRC6lOYeAK0QU3QVP7riIsZuJFpgAQm2QV2BOwaSAw/Bs2bJJrtiazGsxGHrWTesaEf3ll1/kxduoUSPr9oaFagbXcKlSpZIu4yxULUdUBZOc8D2KHyk4xsZyKZp9CbhGRNFFKkY9/EHSAhPo06eP/KIfO3YscGKmCJoAnGEXKVJEMoZP1wULFgSdB0+IPAFXiSh+8fHrj4kmWmACf/31l+TVoUOHwImZImQCy5YtE6VKlZKs8+XLJ7i8LGSUETnRVSIKwohRnyJFCsGtjdqutzZt2oh48eKJq1evajuBqUImAN+k2OyAH/qXXnpJODmIYMiQLHii60T0m2++kRfpwIEDLdgd1qvSwYMHJS+E0KCZQ2DXrl1PJkIzZswoPv30U3MKZikhEXCdiIIStuchtg5NG4FatWrJJTraUjOVXgQOHz4s15diZIq7J4Qv4R2UXnT1y8eVIoooj7gwx48frx9JB+eEKJng9eWXXzq4ldZtGkKVdO7cWfrHTZAggdwRdfHiRetW2GU1c6WIoo+xfKdgwYIu6+7Qm4sIqnAtSIscATyXxooJjErxo9a4cWOBbaa0yBJwrYji1ggX4ty5cyPbAzYpHctvwGv+/Pk2qbFzq/ngwQPpLQrPS9En1atXF1gHTYsMAdeKKH7Vn3rqKbnYOTLo7Vcq/GbCITHNOgQmTJggZ/IhpuXKlRObN2+2TuVcUhPXiij6t2nTpvKXHM/8aIEJTJo0SfLCUhyatQhMnz5dYI0pxLREiRJixYoV1qqgg2vjahE9cuSIvOjq1Knj4C7Wt2lwcl2jRg19M2VuuhHAYxfsfoKYFihQQMybN0+3vJmRbwKuFlEgUTHqIai0wASUk2t6IgrMKpIp4FxbbXNGZIcpU6ZEsjqOLtv1Irpp0yb5q42dObTABK5fvy6wzKZly5aBEzNFxAls2bJF3jlgZJopUyYBT1I0fQm4XkSBEzHqEyVKJG7cuKEvXYfmhjWL+FLCTyvNHgQwew8PZui31KlTC+5A06/fKKJCiIULF8qLq1evXvqRdXBOWJuILyN52a+Tjx8/Ltq2bSv7D2FzunfvLm7dumW/hlioxhTR/3UG/Dti3R1NG4GGDRvKRd9Ys0izHwF46OrRo4e8A8MPYuvWrcX58+ft1xAL1Jgi+r9OwJZGXEwjR460QLdYvwo7duyQvEaPHm39yrKGfglgFApnPLjFx/XfoEEDcfToUb/p+UF0AhRRDyYYiXJroweQAC/Lly8vsmfPHiAVP7YLAfiUyJw5sxTTKlWqiN27d9ul6hGtJ0XUAz9+kfFrPGvWLI+jfOmPwPLlyyWvmTNn+kvC4zYkMHnyZJErVy7Zt3AWzc0oMXciRdSDz927d+UzIszW07QReO2112SIC22pmcpOBObMmSOdmGNgAWfm8MBPi06AIurFpF27dvIXePXq1V6f8K0vAjNmzJC8uM3QFx1nHFuyZIl46623ZD+//PLLAuJqd8PW5fXr18u/a9euhdUciqgXvjNnzsiLBTuZaNoIIAxwhQoVtCVmKtsSWLdunahYsaL8fmTNmlXAl4LdrG/fvk+e+2KErf7C8QdBEfVxFagY9dza6AOOj0NY0YCLEWEtaM4nsHPnTlG3bl3Z52nTprXNihYsy8N1CiH1HH0uWrQorE6jiPrA9/PPP0vY8PJEC0zg3r17Inny5NJJcODUTOEUAoi/1axZM/ldSZw4sejfv7949OiRJZv39ddfy3qGM+L01zCKqB8y8M0YJ04ccenSJT8peNiTgHJyfeLECc/DfO0CAqdPn5ZhyGPHji199Hbp0kXAx4KVLFmyZAIjUSOMIuqHKiZKMPTv2rWrnxQ87Eng3Llzkhe+QDR3Erhy5Yro3bu3SJo0qbwWWrRoIc6ePRtxGLhdx3f55MmThtSFIhoDVizfSZMmTQwp+JEnAXxpsB/75s2bnof52mUE7t+/Lz777DORPn16KV6YY0Dk0kgZRqDwYGWUUURjIAtv4fgFY9zvGCB5fLRv3z7Ja8iQIR5H+dLNBMaNGyewegPfI8zsY1LKbIOnf/wZZRTRAGSxrTFHjhwBUvFjRaBatWri+eefV2/5nwQkgWnTpgnE6IKYIk7X2rVrTSNDETUNte+Chg8fLjt+6tSpvhPwaBQC+HLgi4KtgzQS8Cbw3XffiWLFislrBOFLFi9e7J1E9/e4nYeAG2UciWogixj1RYoU0ZCSSUAAv/x58+YlDBLwSwATt2XLlpViijs9I/1VqOVN+G+EUUQ1UO3WrZvs7B9++EFDaiZBcDSMRsNdxEySzieA8Dx4BITr5dlnnxVffPGFIY2uVKmSLKNDhw4C7hv79esnPf3v3bs37PIoohoQYq0oYtTD9RtNGwHssS5durS2xEzlegIQM7WjCGs6hw0bpjsTjETV81H8R3l6LHuiiGrsKrUzgz4WtQGbMGGC/OXHSINGAloJHDt2TCBoJEam2OzSp08fYfXoCRRRjb2LLW7o2Pr162s8g8nSpUsn6tSpQxAkEDQBBEHEY7R48eLJ713Hjh0FFvNb0SiiQfSKenaD3Tm0wAQGDBggvwCHDh0KnJgpSMAHAWzcwHWUIkUKeS3BnwW2mXoatpheuHDB85CprymiQeCG/0GMRtu3bx/EWe5NipEDbskQXZJGAuEQePz4sfQWhTXI+A7Wrl1bHDhwQMaEwnv8vffee+Ly5cvhFBPSuRTRILFhoTAefFvVW02QzTE8OX5wMCl38eJFw8tiAe4gMHHiRJEzZ04pnEpA1X+46DPbKKJBElfLd7BEghaYwJEjR+TFTl6BWTFFcATUqFQJKP7Dd4PZRhENgThi1GfJkiWEM915ChxQwJELbsloJKAXgUKFCkUbjcLjvlgOXT8AABikSURBVNlGEQ2B+Pjx42XnIVY9LTCBLVu2SF5wRkEjAT0IIMKs5whUvR4xYoQe2QeVB0U0KFz/JkaM+vz58/97gK9iJIAtfniORSOBcAmo0OaYSJo7d66cXKpZs6aYPXt2uFmHdD5FNCRsQm4bw6/f999/H2IO7joNESPBywmRIt3Vc9Zq7QcffCCvo9atW1umYhTRELvi9u3bMkZ9qVKlQszBfafBa0/x4sXd13C2OGwCN27ceBK2GQ6frWQU0TB648MPP5S/itu3bw8jF/ecCneCGI2uXr3aPY1mS8MmAGffmDCKHz++Je9kKKJhdDGCskEU8DyGpo1A5syZRZUqVbQlZirXE4C/UawzhnP0rVu3WpIHRTTMbqlXr54UUj28wYRZFVucPnToUMlrz549tqgvKxk5AmPGjJHXCh6ZWSHgnT8SFFF/ZDQe37Fjh+zoli1bajzD3cnwLBkxyrEHmkYC/gjA4Qju8po0aeIviWWOU0R16ArEqE+QIIG4e/euDrk5P4vu3bvLL8iZM2ec31i2MCgC//zzj6hcubK8Pvr37x/UuZFKTBHVgfzSpUtlp3/88cc65Ob8LOCFB6OMHj16OL+xbKFmAngkpoLZIbCdXYwiqlNPIUZ9hgwZdMrN+dngNi1p0qTi77//dn5j2cKABH766SeRPHlyGSl23bp1AdNbKQFFVKfeUMt3xo4dq1OOzs4GEQIwGkU0VZq7CahAclhDfPz4cdvBoIjq2GVYhoHYQjRtBBA8jI5ctLFyaqq+ffvKH1M4qXn48KEtm0kR1bHbsJMCoyu4y6MFJrBy5UrJy6hQtoFrwBSRJKAC0/Xs2TOS1Qi7bIpo2Aj/zQCOmhGj/o033vj3IF/FSKBYsWKiYMGCMabhh84iAAfd+I5gwOEET2gUUZ2vT7V8Z+PGjTrn7Mzs4HkHXyascKA5nwCehcOZcurUqcUPP/zgiAZTRHXuxvPnz4vYsWMLPO+jaSOQI0cO8e6772pLzFS2JbBgwQL5g4k7D0TPdYpRRA3oSRWj/ujRowbk7rwssaIBo9Ft27Y5r3FskSQAZ8noY0TMvXXrlqOoUEQN6M79+/fLC6Zx48YG5O68LLFLBc+S4YeA5jwC7dq1k9+HTp06Oa9xQgiKqEHdil9ceJ+BH0RaYAJqqQtH74FZ2SXFnTt3RIUKFaSAjh492i7VDrqeFNGgkWk7Yc2aNfLi6dq1q7YTXJ7qwoULIlasWKJDhw4uJ+GM5v/2229yzXTChAnFwoULndEoP62giPoBo8dhxKhPmTKlHlm5Io82bdqIePHiiatXr7qivU5tJJxuw1NX7ty5BWbjnW4UUQN7WC3fiUQEQgObZVjWmLHF5MOgQYMMK4MZG0tg8uTJsg/Lly8vLl26ZGxhFsmdImpwRyBG/YsvvmhwKc7JvlatWnTkYtPuhBcz/AhaKYicGSgpogZTVst3Zs2aZXBJzsh+w4YN8ov4xRdfOKNBLmkF9r5DQIcMGeKSFv/bTIrovywMe4UdGoULFzYsf6dljHAQeJ5Gsz6BP/74QxQtWlQKqFvDYVNETbhO+/XrJy8yzNjTAhPAbC5GNfPnzw+cmCkiRgCbI+BDF5E4t2zZErF6RLpgiqgJPXD9+nU5W8mtjdphw8M5VjfQrElg7ty58ofO6kHkzKBHETWDshBCxag/cOCASSXau5hJkybJLyk8ntOsRUC5fPzggw+sVbEI1YYiahL4Y8eOSVGoW7euSSXav5jnnntOVK9e3f4NcVALWrVqJa9juwSRMwM9RdQMyv8rQ8Wov3z5soml2reoTz75RH5h4YuAFlkCV65ckZ628KyaTrSj9gVFNCoPQ9/h4Tsuwvbt2xtajlMyh98BbBts2bKlU5pky3bs27dP5MyZU6RJk0asXbvWlm0wstIUUSPp+sgbMeqxJY6mjUDnzp3lD8+ff/6p7QSm0pXA8uXLRYIECQQiENgxiJyuMPxkRhH1A8aow4sWLZKi8OmnnxpVhKPy/f333yWvXr16OapddmgMNjzgzgnP8R88eGCHKkekjhTRCGBHjHoswKdpI4CAZilSpOAXWRsuXVKpMDd2DyKnC4wAmVBEAwAy4mPlpIEP6LXR3bFjhxwRjRo1StsJTBUygbt37wr4L8AIlFtvtWGkiGrjpHuql156SWBBOU0bAXgFoiMXbaxCTYVleNie/PTTTzsmiFyoLII5jyIaDC0d06oFy06JeKgjGp9ZgRNGRzNnzvT5OQ+GRwCbGtKmTSt/2LkhJDiWFNHgeOmW+v79+zJs7FtvvaVbnk7PCM+SixQp4vRmmt4+/DDhB8qJQeTMgEkRNYOynzLUw/s9e/b4ScHDngRmzJghv+wrVqzwPMzXYRAYPHiwZNqxY8cwcnH3qRTRCPY/3IghRj23NmrvhGzZssngZ9rPYEp/BFRob07Y+SOk7ThFVBsnw1KpC5mLybUhHjlypBw57dy5U9sJTBWNAK610qVLS45ODyIXrfEGHKCIGgA1mCxxK4/nUXDsQAtMAM+SkydPLho1ahQ4MVNEI4DlYljlgBH9zz//HO1zHgieAEU0eGa6n4EH+ohy+ejRI93zdmKGKpbPiRMnnNg8w9q0YMECETduXOlIxC1B5AyD6ZExRdQDRqRe/vjjj3I0Svdi2nrg3LlzkleXLl20ncBUYsyYMbzjMeg6oIgaBDbYbLHUCev0aNoItGjRQi4Kv3nzprYTXJxKOXFxYxA5M7qdImoGZQ1lIBoono1OnDhRQ2omgXs28KIjF//XAsLS4FEROM2ePdt/Qn4SFgGKaFj49D0Z20Dht5GmjQAEImPGjNoSuywVdh3lz59fpEuXztVB5MzodoqoGZQ1lqFi1C9evFjjGe5Otm7dOjnKgkMX2r8E8Iw9ZcqU4o033hBYi0wzlgBF1Fi+QecOF3mI403TRuDNN98UefPm1ZbYBamUhzAGkTOvsymi5rHWVJKKUb99+3ZN6d2eaN68eXI0CmfXbre+fftKFriGaOYRoIiax1pTSQhih/AhFSpU0JSeiYR4+eWX5Q4ct7KA1/nGjRtLAZ06dWqMGLDFk35sY0QU9IcU0aCRGX+CilF/6tQp4wtzQAkTJkyQArJx40YHtCa4JmDDQcmSJeUPb6AgchBQzNSXKFEiuEKYOkYCFNEY8UTmw8OHD8uLvWnTppGpgA1LxSx07dq1bVjz0KuMH40sWbKIfPnyCThUjsn27t0rrymEWqGIxkQq+M8oosEzM+WM+vXry4v+3r17ppRn90IGDhwoeR06dMjuTdFUf6z7jBUrlgzloSWIXJ48eQSemeKPIqoJseZEFFHNqMxNuGHDBikK2CdOC0zgypUrcl9427ZtAye2eYqhQ4fKa6NHjx6aWtK+ffsnwkkR1YQsqEQU0aBwmZsYcYWeeeYZcwu1cWkQi6eeekpcvHjRxq2Iuert2rWTAqo1iBzCfiRLlkycPHlSZkwRjZlvKJ9SREOhZtI58LqDiYDPP//cpBLtXcyRI0ckLycu8blw4YKoVKmSbN/y5cs1ddS1a9dE5syZo8zGU0Q1oQsqEUU0KFzmJ0ZMoaxZs5pfsE1LfP/992XsKie5FYTfTzzTzJ49uwgmiBxEF3+eRhH1pKHPa4qoPhwNy0XtQJk/f75hZTgp461btzpq9P7999/L23E82gnGY5Waje/QoYPAyFz9YYcXRqd4j1t9WvgEKKLhMzQ8B8SoL1CggOHlOKWAd955xxGOXMaNGyd/EEIJIgcRxSy891+mTJmkKOM4F93rc8VTRPXhaGguKkb9pk2bDC3HKZkvWbJEis+cOXNs2yTMvON5uN5B5Hg7r/8lQRHVn6nuOd65c0c+5ytTpozueTs1Q4zcixcvbrvm3bp1S9SrV08KKCYW9TaKqN5EhaCI6s/UkBzVyOTo0aOG5O+0TLGHHCO51atX26Zp2KkG4c+QIYNhQeSw1Am3+jT9CFBE9WNpaE7YR48Y9Q0aNDC0HCdljgmUypUr26JJEHs4mMazSievc7VFZwRZSYpokMAimbx58+ZydBXMLG0k6xvpsocNGyZ5ISy1lU2Nmps1a2blarJufghQRP2AseLhnTt3SlHo1q2bFatnuTrhWXKSJEmElR25DBgwQPYpY0VZ7vLRXCGKqGZU1khYvXp1GeXSGrWxfi26d+8uRerMmTOWqiw2A6g7CwaRs1TXBF0ZimjQyCJ7wg8//CBFYcSIEZGtiE1KP336tOSl1VmHGc1CncqVKyeSJk0qNm/ebEaRLMNAAhRRA+EalTVi1D/33HNGZe+4fJs0aSJv63F7H2nbsmWLyJUrl4zEabXRcaTZ2LV8iqgNe07FqP/mm29sWHvzq7x79245GsVEUyRt7ty5IlGiRKJOnTqRrAbL1pkARVRnoGZlhxj1uXPnNqs425eDpU7wAh8pw+MXrFvt06dPpKrAcg0iQBE1CKzR2cI9Hr6UgeLqGF0Pu+S/atUqySsS+8XhBAR9FSiInF1Ysp5RCVBEo/KwzbvHjx8LxKiHVx6aNgLFihUTBQsW1JZYh1SXLl0SWE0BR9Fr1qzRIUdmYUUCFFEr9orGOvXv31+OcA4ePKjxDHcnw1IijAiXLl1qOAhsrXzttddEjhw5AgaRM7wyLMBQAhRRQ/Eamzm8nSNGvduiXIZDFaIGV3lGGkQ6ffr0okKFCuL+/ftGFsW8LUCAImqBTginCogrhNHV5cuXw8nGNeeOHTtW8oLzZiMMsY/QH506dTIie+ZpQQIUUQt2SjBV+vXXX+WXFpMXtMAEsFModerU0t1c4NTBpUBkVgjohAkTgjuRqW1NgCJq6+77b+URox4enmjaCMCnJsROL7eCf//9t2jYsKHMU2sQOW01ZSo7EKCI2qGXAtQRsXIgCkOGDAmQkh+DAJ4lx4oVS+gxeocQqx1kuCuguY8ARdQhfY5AZrhNpWkj0KZNGxEvXjxx9epVbSf4SIU1uojAWbJkSXHjxg0fKXjIDQQoog7p5YULF8rRaCQWk9sRIZaFYfQ+cODAkKo/ffp0ET9+fNGiRYuQzudJziFAEXVOXwrEqEdkUJo2ArVq1ZJLkbSl/jfV4MGDpQAPHz7834N85VoCFFEHdf1XX30lv9wrVqxwUKuMa8rGjRslLyxL0mqtWrWS5xgRRE5rHZjOWgQootbqj7Brg5Fo0aJFw87HLRmUKlVKkyOXs2fPysXzyZMnF7t27XILHrZTAwGKqAZIdkoydOhQOVJiREdtvaaeJc+fP9/vCdu3bxd58+aV++4ZRM4vJtd+QBF1WNcjiF2aNGlE1apVHdYy45oDt4L+HLl89913IlWqVOL99983rgLM2dYEKKK27j7flVcx6s+fP+87AY9GITBp0iQ5el+3bl2U46NGjZLH+/XrF+U435CAJwGKqCcNh7w+fvy4iBMnjmjdurVDWmR8MzDazJQpkxzBY5lY586dpYAyeoDx7O1eAkXU7j3op/4qkiT8jtJiJrBkyRIpmFg3qv7gA3TTpk0xn8hPSUAIQRF16GWwY8cOKQiIa06LmUClSpWeiKcSUYxMaSSghQBFVAslm6aBV3WE5aXFTACbFJR4ev5/+PBhzCfyUxLgSNTZ1wAW3UMUMHFC80+gYsWK0US0SpUq/k/gJyTgQYAjUQ8YTnwJD0OZM2d2YtN0aVPPnj2lgL7xxhtPhBSe78+dO6dL/szE+QQoog7vY8wuYzS6ePFih7c0uObdunVLOmYGGxVE7vbt24KL6YPjyNScWHLFNaB227iisRoaCQ9OGHlmzJhRN8fMGoplEocS4EjUoR3r2SwVox4z9m43PCfOkiWLePvttxlEzu0Xg07tp4jqBNLK2WCWGQvJEX3SzTZx4kQZRqVly5aGYsCSqUWLFhlaBjO3DgGKqHX6wtCaqBj1p0+fNrQcq2beq1cv+Wx45MiRulURkVa999yfPHlSloP/NHcQoIi6o5/lbHOSJElE06ZNXdLi/zYTcd8bNGgghQ3x4PUyxLVKliyZzPfatWtPssV++xIlSjx5zxfOJ0ARdX4fP2mhilEPYXGDHTlyRMY/SpEihdi/f7+uTYZQKp4QVGW4lfd8r47zv3MJUESd27fRWgYhwZIe3No63VauXCleeOEFUbhwYd2DyOF5J0ah6tbd8/knnj3T3EWAIuqu/haIUY8Aa042hElBJM969eoZ0kwIJWLXw/LkyfPkNcSUgQINQW7pTCmilu4e/Su3fv16ORodN26c/plbIMc+ffrI9hnleAUiiVGoeg6qbust0HRWIUIEKKIRAh/JYt97772QolxGss6ByobLv8aNG0sBnTNnTqDkIX0O4USMJTUKRSYNGzbkRFJINJ1zEkXUOX2puSUqrhBCXzjBTpw4IRfP4xbeyCByEE88U/b+Q3gRmnsJUERd2vevv/66fJ5n9+YjpEf27NlFrly5xIULFwxrjucoFLPv6k8Jq2EFM2PLE6CIWr6LjKmgilFvZ+/tU6dOFQkSJBBmuK3DbbuvmXeIKUamXFxvzHVqh1wponboJYPqmCNHDlG2bFmDcjc2W7UDq1u3bsYWJMSTpUy+Zt7VMieuDTW8GyxbAEXUsl1jfMVUjPpjx44ZX5iOJTRp0kSO/iZPnqxjrv6zwgJ6X6NQdQZGor4EVn3O/84mQBF1dv/G2LqrV6/KGPW4VbWDnT17VpQpU0YK6IYNG+xQZdbRBQQooi7o5JiaqGLUw0mxlW3z5s0Cjx8wInSrExUr94+b60YRdXPvCyFwK48Y9WY8WwwV9axZs0SiRIlE6dKlQ82C55GAYQQoooahtU/GLVq0kLfIVqzxoEGDZN1at25txeqxTiTAuPO8BoRQMer19LWpB9fmzZtLAR09erQe2TEPEjCEAEeihmC1X6Y1atQQcBlnBcOieUTcxKz38uXLrVAl1oEE/BKgiPpF464PVIz62bNnR7ThGBVj91HKlCkZRC6iPcHCtRKgiGol5YJ0CN6WM2fOiLV07ty5At73ixQpIu7duxexerBgEgiGAEU0GFoOT6ti1GM/utn22Wefydt3hPKgkYCdCFBE7dRbJtQVMepLlixpQkn/FtGqVSspoJiJp5GA3QhQRO3WYwbXV8WoP3jwoMElCenYuHz58lJAcSvvbdiPDifS+KORgFUJUESt2jMRqtfdu3flrqA6deoYWoO9e/eK3LlzSy9Me/bsiVIWImbC+TF2J8FzPGbpEZpYeZOPkphvSCDCBCiiEe4AKxavPCRduXLFkOohFhFEEiJ6/fr1aGV4R8yEeEJQcZxGAlYjQBG1Wo9YoD5w9IFZ8o4dO+peG4wyMbKsWrVqUHnD+TGEl0YCViNAEbVaj1ikPh06dJBip2d1VJx2OD0J1iCiiKxJIwGrEaCIWq1HLFIfFaN+yJAhYdfo9u3b8lYcI9ApU6aElB9u5yHCNBKwGgGKqNV6xEL1wZrNxIkTh1WjAwcOCARyg4CGGooEo1DPMMVhVYgnk4DOBCiiOgN1UnYqRv20adNCatayZcvkfvwsWbKIv/76K6Q8VJx3zObTSMCKBCiiVuwVC9UJMeqzZcsWdI3GjRsnR5/wRB+qQUAxgmX8olAJ8jwzCFBEzaBs4zJUjPoff/xRcyu6dOkixa9t27aaz/FOqEagjF3kTYbvrUaAImq1HrFgfRCjvmjRogFr9uDBA1G9enUpoGPGjAmY3l8CJaC8hfdHiMetRIAiaqXeiHBdcNvcr1+/aLVQMep/+eWXaJ+pA0ePHhUFChSQAgq3eqEahBO38JUrV5Z1QX08/3hrHypZnmcUAYqoUWRtli92BWXOnFkKmK8RIILEVatWzWerVq1aJVKlSiVSp04tjh8/7jON1oMoG1s9/f3x9l4rSaYziwBF1CzSFi9HLWb3N5EzbNgwKbDnz5+P0pJJkybJ41pu96OcyDck4BACFFGHdGQ4zcAoFFsq1bNIbM30Nuyjx2izWLFiYsCAAWLnzp3io48+kgLaqFEj7+R8TwKuIUARdU1X+28odgJhRxAMt9EYlXobdjAlTJhQiiZGq+pv8ODB3kn5ngRcRYAi6qrujt7YkydPSkFUEzYQUV/ekpo0afJEOJWApkmTJnqGPEICLiNAEXVZh3s3t2HDhnL0qY5jFAoh9TYsc1Li6fnflys773P5ngScTIAi6uTeDdA2jD4hiJiVh9Nj/OG1L5dz3bp1iyaihQsXDlACPyYB5xOgiDq/j/22ECNOuJfD6FP9YWQKYfU2eGKCyKpRaIYMGRi2wxsS37uSQPRviysxuK/RahTqvSbU33FFaNu2bWL16tXi0aNH6hD/k4CrCVBEXdr9mI3HqNPbsNwJo0010eT9Od+TAAlEJUARjcrDFe+wHhRCiZl5X4bPfK0V9ZWWx0jA7QQooi68AnAL730b74kBo1B/AuuZjq9JgASE+H+CaQcnxtJFVAAAAABJRU5ErkJggg==[/img]
Triangle DEF is formed by connecting the midpoints of the sides of triangle ABC.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWIAAADvCAYAAADIBd7IAAAgAElEQVR4Ae2dCbiN1fv+v4pIA4kGZKiUkJJU0iSESnMIlZRmRYUiEqWoCCUSkqnBUBRfSqFfkygaaFIpQ5pUSCXW//qsf+/+7rPb55y993nHve/nuvZ1zt7v+671rHu9+97rXetZ9/MfIxMCQkAICIFAEfhPoLWrciEgBISAEDAiYt0EQkAICIGAERARB9wBql4ICAEhICLWPSAEhIAQCBgBV4n4q6++MgsXLoy9Am6bqhcCQkAIRAIBV4n45ptvNv/5z3/yvKpVq2bef//9SIAhJ4WAEBACQSDgKhGfeuqp5vLLL4+1gxHyUUcdZcqWLRv7TP8IASEgBIRAXgRcJWJGw+PHj89Tw9ChQ+0IOc+HeiMEhIAQEAIxBFwj4tdee80SbuI0BNMVZcqUiVWof4SAEBACQiAvAq4RceLIF0Lu16+fJeeZM2fmrVXvhIAQEAJCIIaAa0TM3HDiQt3RRx9tmCeWCQEhIASEQP4IuEbEVatWNXfddVesJqYqWKiDjGVCQAgIASGQPwKuEPGmTZuSTkE488b8lQkBISAEhEByBFwhYodwE6chnM9FxMnB16dCQAgIARBwhYiZkmBqItGYN1bERCIqei8EhIAQyIuAK0R87rnnGnbQESXhvHgPCWs0nBdwvRMCQkAIJCLgGhGzq855ETtMOBtzxzIhIASEgBAoGAFXiLjgKnRUCAgBISAECkJARFwQOjomBISAEPABgZSI+NtvvzVz5841GzZs8MElVSEEhIAQyC0ECiXivn375tkxN3DgwNxCSK0VAkJACHiMQIFEvGTJkjwk7GxhXrlypcduqXghIASEQO4gUCARDxs2LCkRjxs3LncQUkuFgBAQAh4jUCARz549OykR77///mbatGkeu6bihYAQEAK5gUCBRAwELVu2zEPGlSpVMm3atIl9NmDAgNxASq0UAkJACHiEQKFETL1MRXTp0sX06dPHQMSDBw82y5cvN7fccospX768JeV27dqZ7777ziM3VawQEAJCIHsRSImI45s/duxYS7yLFi2yH//www/mwQcfNHXr1rWf16tXT9ua4wHT/0JACAiBQhBIm4gpr3v37mavvfYyf/zxR57ip06dGpvKKFWqlBk5cmSe43ojBISAEBAC/0YgIyLetm2badWqlWnatOm/SzTGLF682Fx11VWmRIkSdpTMtMb27duTnqsPhYAQEAK5jkBGRAxo5KSrUaOG6d27d74YfvHFF4YNISixEYPcpEkT88EHH+R7vg4IASEgBHIRgYyJGLCmTJliCXbWrFkFYscIevTo0aZRo0b2/IoVK5pnnnmmwGt0UAgIASGQKwgUiYgBydkCvXHjxpQwe/HFF03r1q0tITNKjs9zl1IBOkkICAEhkGUIFJmIwQNibdCgQVrQvPfee6Zr166mXLlylpQpY+3atWmVoZOFgBAQAtmAgCtE/Mknn9jwtRtvvDFtTBhJP/DAA+bII4+0hMzfl19+Oe1ydIEQEAJCIKoIuELENP755583JUuWNBMnTswYC+acmzdvbgmZsoYPH55xWbpQCAgBIRAVBFwjYhp8//33WxL97LPPitT+hQsXmk6dOpnixYvb8q677jrDgp9MCAgBIZCNCLhKxADUsWNHc9hhh7mC1eeff263VZMhmoU9cuIxtywTAkJACGQTAq4T8TfffGNOOOEEc+mll7qGE6Phxx57zDRs2NASMupvkydPdq18FSQEhIAQCBIB14mYxsybN8+ULVvWPPLII663jZjliy66yBIyo+SCNpS4XrkKFAJCQAh4gIAnRIyfjqj8u+++64HbxixbtszcfPPNlvAh5AsuuMCsWbPGk7pUqBAQAkLASwQ8I2KcZpGNaQQvDenNQYMGmdq1a9tR8hFHHGETnXpZp8oWAkJACLiJgKdEjERm48aNzTnnnOOmz/mWNWnSJHPGGWdYQt5tt93MkCFD8j1XB4SAEBACYUHAUyKmka+//ro58MADzb333utbm1977TVzxRVXmF122cWScufOnc3mzZt9q18VCQEhIATSQcBzIsaZMWPGWEJ85ZVX0vGtyOd++umndjHvoIMOsvUjOkRmapkQEAJCIEwI+ELENPjWW281iMVv2bLF9/b//vvvVqSesDoW9vbbbz8zYcIE3/1QhUJACAiBZAj4RsQQ8Jlnnmk3ZSRzxK/PXnjhBRthASHz6tmzp19Vqx4hIASEQFIEfCNial+6dKk5+OCDTY8ePZI64+eHhNWROaRMmTKWkFlQXL16tZ8uqC4hIASEgEXAVyKmRiIbGIlOnz49FF2wYcMGq5FRq1Yt69fhhx9uZs+eHQrf5IQQEAK5gYDvRAysd955pyW9sOkPP/XUUzYPHz8UCA4NHjw4N+4CtVIICIFAEQiEiHfu3Gm3KR999NGBNj6/yhcsWGAuv/xyU6xYMfuDQSjcpk2b8jtdnwsBISAEioRAIESMxytXrjR16tQx11xzTZEa4OXFhL/16tXLVKpUyRLy8ccfb958800vq1TZQkAI5CACgRExWM+YMcOKyY8bNy7U0BP+hoDRcccdZwm5QoUKZuzYsaH2Wc4JASEQHQQCJWJgYscdc7Iff/xxJFCbOXOmOf/8863P+E18tEwICAEhUBQEAidinEe7uHr16kVph+/XskPvhhtuMHvttZclZWKkmcqQCQEhIATSRSAURPzVV1/ZLNBt27ZN1//Azyf8beDAgaZmzZqWkGvUqGEYNcuEgBAQAqkiEAoixtm5c+dabeGhQ4em6nvozmPbdJMmTSwh77rrrpagQ+ekHBICQiB0CISGiEEGEmbeNeqRCYgbMd1CW3jxP5KgMiEgBIRAMgRCRcQ4SDhbuXLlkvkauc8++eQTc/vtt5uKFStaQibqYvHixZFrhxwWAkLAWwRCR8QbN260wkAtW7b0tuU+lr5161YzYsQIOw/OCLl8+fJm9OjRPnqgqoSAEAgzAqEjYsBatGiRFZPv169fmLHLyDc0Ns4999zYtAV599hpKBMCQiB3EQglEdMdo0aNsmTFIl422jvvvGOuv/56s+eee9p2Nm/ePDKx1NnYH2qTEAgSgdASMaB07drVEH3wyy+/BImRp3WvX7/ebmo57LDDLCEfeuih5rnnnvO0ThUuBIRAuBAINRH/9ttvpkWLFubEE08MF2oeeTN+/HibbJV5ZPLt9e/f36OaVKwQEAJhQiDURAxQ7GBDTL5bt25hws1TX+bPn286dOgQm0e+5JJLDBtHZEJACGQnAqEnYmBHJ5hR4tNPP52dvZBPq1atWmWzmRxwwAG2/Q0aNDCvvvpqPmfrYyEgBKKKQCSIGHCRo4SM16xZE1WsM/abfH/Dhg0z9evXtxjsu+++5tFHH824PF0oBIRAuBCIDBH//fffNuln7dq1w4Wgz95MmzbNkF+PHyVeN954o/nrr7989kLVCQEh4CYCkSFiGv3hhx8aiLhTp05uYhDJsgh/u/baa03p0qUtITdr1sysWLEikm2R00Ig1xGIFBHTWYR27bbbbtqZ9s+dS/jbgAEDDKpvjJAPOeQQM3Xq1Fy/r9V+IRApBCJHxKAL8UA6GgHmvdfIdHLaaadZbMi317dv37wn6J0QEAKhRCCSRAyS7du3N5UrVw4lqEE7Rfhbu3btLCHzg9W6dWvz7bffBu2W6hcCQiAfBCJLxKtXrzbHHnusufDCC/Npmj4m/K179+5m//33t6QMXpC0TAgIgXAhEFkiBsaXXnrJlClTxgwePDhcqIbMG8LfHn74YVOvXj1LyMiMEg4XZWMXIqJQiS+yvciEQNQQiDQRA/ZDDz1kyQXFNlnhCLDYefbZZ8emLYi8IEt11Oyoo44yVatWtZKpp556auyviDhqPSl/QSDyREwjOnfubJN4EmssSw2Bt99+24rw77777paUmzZtapYtW5baxQGftWnTJuuzcgMG3BGq3jUEsoKICeE6+eSTDWQiSw+BdevWmbvvvtuGvbGwh67HpEmT0ivE57Nfe+01S8Qa/foMvKrzDIGsIGLQQYMBTYbevXt7Bla2F/zEE0+YU045JTZtwbbyMNpdd91l1wbC6Jt8EgKZIJA1REzjR44caUlk1qxZmWCha/5BYN68eQbFN0bIvC6++GITptEnGU6qVav2r4U6daAQiCoCWUXEdMJNN91kyeOnn36Kap+Exu+VK1eaW2+91VSoUMFiiujQnDlzAvePRbrEhTpSTsmEQFQRyDoiJpvHGWecYRN1RrVTwub35s2bzZAhQ8zRRx9tCXmfffax0SpB+MnInFE688QyIZAtCGQdEdMxRASw6IQymcxdBJ599llz1llnWTKEEIlYIZOKX0akBPUSOSETAtmCQFYSMZ3z5JNP2i/sxIkTs6WvQtWOt956y5JwyZIlLc5NmjQxKMJ5bSzUMS0hEwLZhEDWEjGd1LNnT0sSbIeWeYPA2rVr7aIZTyCMVKtXr25/BL2pzdiNG5dffrlXxatcIRAIAllNxH/++adhhf3www8PBNxcq3TMmDHmpJNOsoQMKffo0cN1CNjSTsQEKnPxL9crUoFCwEcEspqIwRGpTMTkL7vsMh9hze2qCH9r06ZNjJAvuugi88UXXxQZFOaFmZpIfKE7IRMCUUYg64mYznnmmWesmLzyvPl7qxL+dsstt5jy5ctbUj7mmGOMYrz97QPVFg0EcoKI6Qq28fK4HBU9hWjcPql5Sfgb4kx169a1fcD0wqBBg1K7WGcJgRxAIGeImL5ktxjboGXBIUD4W8uWLWPTFldddZX5+eefrUPff/+9JWg2Z0jQJ7g+Us3+I5BTRPz5559bMXkW8HLV3n//ffP8889bfeKFCxcGBgPhb5BwiRIlLCk3atQoJmDPkwuv22+/PTD/VLEQ8BOBnCJigGWOkkfjgQMH+olz4HWx0NWxY0dLcI5+LzgQeRDk5gjC38itV7Zs2dgo2SFi/v7666+BYycHhIDXCOQcEQMoGT34kqPYlisG2fLIHy/ew+gYMh46dGjgMJx55plJifjDDz8M3Dc5IAS8RiAniRhQO3XqZBBFJ9Y4l80ZHQeFwdSpUw3TEvGj4MT/yUv4ySefBOWi6hUCniOQs0TMIzFi8jya57JBxH7vVPvxxx/tbjwnrI2M08QeE+vtkDBzx8cff7zp2rWrIccenyM6NGPGjFzuLrU9SxHIWSKmP1955RUbRcFW6Fw0v5XM3njjjZjOceXKla2I/2effZYHet4vXrzY8LdUqVJW9Q1RoQcffNAceeSRlpD33ntvc++99+a5Tm+EQJQRyGkipuMeeeQR++XOxZEWCTj9iCAZN26cYTMHo1q2QLMVevv27YV+bwh145oFCxbEzmVzTvPmze3nHLvyyisNYW8yIRBlBHKeiOk85DL5Um/cuDHKfZmW70xHQMReRUx8++23VnSJxUCwvfTSS+0TSFpOGmND2A455BDDdEa8vfnmm3aev3jx4rb8xo0bG2XyjkdI/0cJARGxMXZDAWLy9erVi1LfZeyrlyTMdM95551nybFKlSo2NK2o6nf0zQUXXJC0vRB+nz59rDQmhI9E5qhRo5Keqw+FQFgREBH/0zPMXyLheO2114a1r1zxyysSRscDcSXIkAVQhHh27tzpis8bNmww++67r92mXlCBjz/+uGnYsKH1AT9uu+02s2PHjoIu0TEhEAoERMRx3TB27Fj7Jc5WNS+3SZgFNXIEli5d2uJ2xRVXGK9267300ku2DnYFFmZz5841KL5BxrwYTX/00UeFXabjQiAwBETECdB3797dfnkTV/MTTovcWzZtQEqEgMXr+Dr/s7kjVZs9e7Zp0aKFLQ9t4P79+5s1a9akennG5w0YMMDst99+5uuvv06pDMiXTSzOrj3mxFkAlAmBsCEgIk7okW3bttlIAjJOZJORbDNRxzf+ffyOu2TtZuMLIWSHHXaYJWBSIwWRhur88883zZo1S+Zivp854W/O1Mlee+1l7rnnnnzP1wEh4DcCIuIkiDM6rFWrlo15TXI4pz764IMPzNVXXx0T5yFZ6P/93/8FhsGWLVvsghxPLpkY4W8s/jnTFuywXL9+fSZF6Roh4BoCIuJ8oGTr7W677WZVyvI5Jas/fu655wyjXgiL8DFEktatWxeKNjMPjV+TJk3K2B/C35jT3mWXXWxZTNHExytnXLAuFAIZICAiLgA0Ht35wi9ZsqSAs7Ln0C+//GIf2Ykeod2MHPlBCqMNGTLELhIWVRTICX876KCDbJsJuVMmlzD2eHb7JCIupH/btm1rQ6cKOS3Sh9955x2rNwH5MkIkhO/tt98OfZs6dOhgw9X+/vtvV3wl/O2EE06whAwWt956a86LQrkCrAopFAERcSEQofpVv359g0xjttlTTz1lhY8gnRo1alh50KjtLmQu3+3Yb8LfCHkDF15sUFm+fHm2db/aEyIERMQpdAaxq2zVJe9d1I3NEb179zaI7kAyhKFFOaTr3Xffte147LHHXO8awt+Ik3a2aZNzb8qUKa7XowKFgIg4xXvg/vvvt1/4+fPnp3hFuE5jgQu5ScgXickbbrjBQGLZYKNHj7btYgHOCyNLyAMPPGAjacBvzz33NMQ0y4SAWwiIiNNAklV2RGa2bt2axlXBngpJOfOehx9+uM2mnCigE6yH7tR+zTXXmDp16hgWHL20p59+2jRt2tQSP6TMPfHNN994WaXKzgEERMRpdDJfOGQcySgRZvvyyy9Njx49Ysk4md/OBZnPBg0amPbt2/vSNWiTsGW8WLFilpQR2EfcXiYEMkFARJwmakxNHHDAAeaWW25J80rvT2eR6eKLL7bEULJkSdOlSxeTztZl7z30toZVq1aZXXfd1U4jeFvT/0rnx/nOO+80lSpVsrgTBofGtUwIpIOAiDgdtP45d9iwYfZLx6aHoI3QrREjRtjIDh6ViSJ4+OGHPX9ED7rd+dXPJg9wCGIun2mg4447ztaPD926dYvUNFZ+mOpz7xEQEWeI8fXXX2+/cEFtj/3444/tF93J59aqVSsza9asDFuTXZfxtIIYEXkJg7A5c+YYNDEgY15kQVm6dGkQrqjOiCAgIs6wo3744Qe784wFIj9t5syZMeF1slCjLlbU3WV++u9XXWxZ9iMNVEHtoV+YHkJkCEIm515RtmUXVJeORRsBEXER+u/111+3YvLkTfPSNm/ebJNoEsfKFxryHz58uEEAR5YcAUbDJBnt27dv8hN8/JRIjsGDB5uaNWva/ttjjz2sdKiPLqiqkCMgIi5iB5EIE3Lkr9vG4yz59JwRFSM8BNJlqSHA0wN9M3369NQu8OEstDscMSV869ixoyHKRZbbCIiIXeh/NAn4Uq1cudKF0ozd6XbWWWfZMtk8wJwnEQGy9BEgnx1plsKGH1Kil112me1j7p1TTjlFP7Lpd2/WXCEiTqErEU3v169fnld8WBgbPBitErqUqZESnt17RxxxhP1yMg1BGNQff/yRaZG67h8E+FE7/fTTQ4mHE/5WsWJF2+9sPScKRpZbCIiIU+hvctgxaiFonxcpd3iPGIyTjn7ZsmU2dIxcaekY23LZFVaqVClbJqvtxAPL3EOADB0HHnhgKGO/41tJ+BubUri3eHXt2tWwvVqW/QiIiFPoYyITIN94c+YfOeYYK+KIyZNSqDCbPHmyTfnDF45FJTIOZ1uevMIw8PP4yy+/bMltwoQJflabUV2Ev/Ej7xDyOeecEwlZ0owaq4ssAiLiFG4ERsFsZ000PiMxZbyxy4ov0H333Wd69eplSM3jGCLkiMUceuih9px69eoZVMO2b9/unKK/HiLA1A87DqMiduSEv7FOwD1FtEwQeQI97BIV/Q8CIuIUbgW+BGRBTjRnyiJ+vnjnzp12M4EzmuEv+hTkRmP7Le8vvPBC6RIkgunT+9atW9vdb4QERsWc8DcncWvp0qWzQpI1Kvj74aeIuBCUIVnIM55snUvIjJx4jDlfPkt8ETuKEM8XX3zhXK6/ASHAEwlJUKNohL81btw4dn/xVKYprSj2ZF6fRcR58fjXO0bCkGoyS3bMGSUnEvFDDz2UrAh9FgACpIGif6IszpMY/nbyySebF198MQA0VaUbCCRnGDdKzpIyGHEwR5zMOFa1atU8h8jqkEjCvN9nn32sSpe0a/PAFdgbQsToF55qomxr1qyxGVdQBKQ9hMEhSiWLFgIi4kL6i2iJ+MgI53Rii1moS3bMyf4cT8iDBg0yRx99tP2yQODo2cqCRQBRd+K2gxJucrP1rE2MGjUqpsLHvce9+dNPP7lZjcryCAERcSHAckMTqhZvxA4jKkMuMyeOOP44/zMXjEwmYVMs1iGPiPGZs2uOub6wpqtPbE+2vueHlkzd2WRsg2eDkTMQQJmPqQxZeBEQERfQN85iHKNfxyBlRraQcLIFPOe8+L9s0ODRESUux1jUu/rqq23+OBaPEIXxOs2PU7f+/g8B5EQhLELbss0++OADq1VClAVtrF27tiFztyx8CIiIC+gTZ4qB0a8zrcANzdRCPDkXUETskLOwlzgCZs6Y7NDVq1e3Ma6QtWQtY7D58s+4ceMsUc2ePduX+vyuhKc2psZq1Khh24l8Klv2ZeFBQERcQF9AtoyK41/5TUUUUEzskCMmn9+C3RNPPGGnMSB7dlaxw0rmDwKo3KEVku2hYFOmTLHTatxjvBAeCpsgkj89Hq5aRMQ+9sfGjRvttmayKRdkTGW0adPGflHq169v0CAgJZLMWwROPPFEc/bZZ3tbSUhKR0v70ksvtfcYhExCXGV4Ca5zRMQ+Y79o0SI7DcFIpDBjigIJTNIhVahQwYYpEa4k8wYBtqAjvtS7d29vKghhqV9//bXdir///vtbUkYciZyHMn8REBH7i7etjREuoxDCjVIxFvHYEEKqHedxUqvgqSCX/jlEtYBx4lx++iVF64odO3ZY3RP0T2g/r5tuusnwFCfzHgERsfcYJ63BEZNPd2Hu6aefNi1atLBfFIW/JYW2yB/27NnTxoi/9957RS4rigUkhr8xXcNUhsw7BETE3mFbYMlo5CJvSFhbJsaImFx5CAk54W8///xzJkXpmiQINGvWzO6o/P3335McLfgjFncXLlxoX0VZ3C24Fu+POuFvRFkwQq5Vq5aJgoyo98i4X4OI2H1MUy5xyZIl9uYuSrZh5vhIkFmlShWFv6WMfOEnMh1EiqVkOyfzu5pwR3ZbEmPOtnj+8j5xQ1B+14f1cyf87ZBDDrGEzDw6bdUCsns9JiJ2D8uMSiLAHjF5NzYUMPfcsGFD+2VRotGMuiPPRfPmzbNYPv7443k+z+8N5MRoON6IOU/UrI4/HrX/E8PfiLxId3otam32w18RsR8oF1KHIybv1jwcc3ykbOJx8phjjrGLgn/99VchXuhwMgT69+9vihcvbhYvXpzscKGfQcz0Q6q7MAstMCQnJIa/Efr3wgsvhMS76LkhIg5Bn/GIR9wwW1ERb3HLVqxYYR+teUR2wt/S3RHoli9RLofNNcRzZxJB4MiiRnmuuKC+c8LfuL/4wWHNI1kShYLK0DFjRMQhuQuQz+TLTiSE20YCSrQsWGzhy0IMs8LfUkeZ0C7m4Mmykqrxg/fkk0/aaQmmLLLdkoW/sV1/3bp1Wdd0L35URcQhuk2mTZtmF3huv/12z7xijo+IAAhZ4W+pw+xkXhkyZEiBFzlTEeDLKxc1HRCoJyLIwQC1wUyndgoE28eD9CuaM06b+FutWrW0NWfyc1lEnB8yAX1+77332s72WoCGHX4dO3a0dbEajijMDz/8EFCro1GtI9xUkAYIoyW+tLyYlkBmE8EoL0ZRYUeNqbEbbrjBRvNAXGg/85QQNXOml1h4pV+Z7+evm086IuIQ3hUIlnPj+hEX7GR4qFSpko3eQPxm+fLlIUQlHC61b9/ekMRz9erVKTkEAdOXuTxvyn1MVNDBBx9ssSCTNiGXf/zxR0oYBnkShEv/QcZemojYS3QzLJsvOWLyRDz4aY899pgVsOfGU/hb/sgzsrv44ovzPyHhCOm03Bw9JRQfqbeTJ0+2MdbcY7z4YWPjSFiNvssvVZqbPouI3UTTxbIIQWMF+rrrrnOx1NSKQoXr/PPPt18UJ/xt27ZtqV2cA2cRNwuJENpWmPEYy7lR39RRWDvTPc6ccYcOHSw24EP8+/PPP59uMZ6eT5/hmx+hhyJiT7uyaIWzMMSNMGnSpKIVlOHVzhbXPffcMxb+RgoomTFoR9M3zz77rIWDR1jmglmcg1B4de3a1UZN+DGiimqfEF1yxx13mPLly1s8UYErbEHUr7ayqzIxObBXdYuIvULWpXIdMfkg43/RxWCODx1lyIfdVCz25bqR6oqsySxKMRfMPDCkG//yem4xW/qAWPqRI0fmyYTDegXSpEGZ049+1C8i9gPlItSxYcMGG25GZEMYbOLEieb000+3hEw4D+FwuWzHHnusadmyZSQWnqLST0QMkfCUH31eZ555ZiA//CLiqNwxPvn56quvWjH5du3a+VRj4dUwx+dkeHDC3zLZeVZ4TeE+g6iTXXbZxfTo0SPcjkbQO6J3eCIsUaKEJeSaNWt6Hr0QDxML1pCxH6YRsR8ou1AHEQ2MDh555BEXSnOvCPLvMcfHwiLiRTxOLlu2zL0KIlAS88T0zdixYyPgbfRc/Omnn8x9991nByPgzH2GPsuWLVs8bYwTN878v9cmIvYaYRfLd8Tk/VjFzcRtfiTYps2XhdFELuVAI6XVXnvtZd54441MoNM1KSKQGP7GUyJz9F4Zi3Wo57ERxdGYJpWU22s2ImKvetCDctHIZesoK8xhNub4nC2upN5hNL9169Ywu+yKbzzGEv/9448/ulKeCskfgcTwtxNOOMGTEEEWYdlRh3AWAwxe7JYUEeffNzlx5O2337biPezfD7sRb8scHxke+PHo1atXVqerZwcZo2LaLMhPigwAABErSURBVPMHASf8DRF/SHK//faz+R39qd29WjQidg9L30riMYkFDHQpomCEv+ErKZ34srDI58e8WxDYzJ0717Zx2LBhQVSfs3UmC39D54I1jCiYiDgKvZTER0dMPmqERvgbj/AQMuFvQW1WSQKpax+xqaNYsWKGDB8y/xFIDH8jvJD53TCbiDjMvVOAb3/++acVk2dkHMXsG2R4YKEFQib8jQ0j69evL6DF0TpE7Cs77RBOlwWDgBP+RoYV7jM2JI0bN84688ADD5gjjzzSKsKFQapURBzMPeJKrawWE6XAAlFUjZ1TxOCS4cEJf3v33Xej2pyY3zwqE9KHCL8sWAQSw9+I+4aY41+sXwRpIuIg0Xeh7meeecbsvffepnv37i6UFmwRI0aMiG1xJeoibCIw6aJDFhS+7FGZy0+3fVE8n6kwFlTjSZj/DzrooECbIyIOFH53KnfE5KNOXA4azPERFcIXhPC3Rx991LDgF0V76KGHbDumT58eRfezzucJEyaYPfbY419EjGZIkCYiDhJ9F+t2sm1kU5YNwt+uueYaO2XhhL+tWrXKRdT8Kap169Z2Hpy8hDL/EWD6q0+fPgZlN37cmQJLHBHfdttt/jsWV6OIOA6MKP/7+eef27liFiCyzTZv3mzuueee2BZXwt9eeeWVSDWTBUk0nrdv3x4pv6PsLBFFl1xySYx0EWhiKg9jga569eqmcuXKoZjWExFH+U5L8J1Hen71O3funHAke94yx8fiJCMawt941IyCoe2Mz+hyyLxFAK3o4447LkbACNCHOQsIaIiIvb0nfC/dEZOPYpLGdMBiIaxt27b2y0YutIEDB5q1a9emU4Tv5z7++OPW32zvG9+BNcZ8+eWXhuzn5cqVsxijD8HaSVRCO0XEQdw1HtdJeiVGX0xXRNV4rExlPz/ky/weX0BiqtlNxTbwsNqVV15pn1rC7GNYsUvm1/z5881FF11k73fueTQnZsyYkezUUH8mIg5192TmHOTUrFkzU6VKlcwKCPgqR34w3YSbqL8xR84XkvC3sEYq1K1b1/YPgjKyzBBASIqIGvqaF5nPV65cmVlhIbhKRByCTvDCBRazWIxgxT5KhsQnj5VFyXz84osv2qwZfEH5sg4fPtygXBcWY6SPb126dAmLS5Hw49NPPzVIwTpxwAj8DBo0KBK+F+akiLgwhCJ83BGTj5IADRKDjITRo0h3RJzYVYSLsXC56667WvW3nj17mo8//jjxtEDeP/3005aMwyb0HwgYhVRKRnP0rZ3R78knn5x1Wtci4kJugqgfRrCcG3jp0qWhbwrECxFjbhCx02AyObBww1QNWLCKztxi0NatWzdTunTpyIXi+YHbjh077JNMnTp1YgTMj2qU1z0Kwk1EXBA6WXAMjVzmSxG2DrOxOIePzgKdm0Qc324yPJx44on2y00diMCgCxGUNWzY0PAKMltxUG1PVi9PMTfddJMpVaqU7SPifIkEynYTEWd7Dxtj3nzzTSsmf8YZZ4SytSxaVatWzaajdxz0ioid8klpdPHFF9svO+FvAwYMMCQC9dvI5lGyZEm72OR33WGqj+35KNY50w+NGzc2c+bMCZOLnvoiIvYU3vAU7ojJ33333eFx6h9PSEXDHGC8eU3ETl3r1q2zO6sYjRP+du2119ofLue4H3+ZA4WAkALNJUPKFS0O5ClpP/iT3cR5KsolLETEOdTbjph8mLYHz5w5034JGRE5yRn5i5Yv+hn871eYF+JCtWvXtv60atXKPPfcc77dHX379rX1gke2GzrBxLqziAoBs/2byJZcNhFxDvX+tm3brJg8Nz//h8FYoMOfgl5+ZyFhhMo0Dj7xg0DWXjRtvbbmzZvbOOgoChulgg0/bMS3O33N/y+//HIql2b9OSLirO/ivA0kThcx+eOPPz7vgZC982tqoqBmE+rGSj3EQXJKNJ+91CxgOy47BNkptnPnzoJci8yx33//3dx3330xwSYkKFmM0+Jk3i4UEefFIyfeOWLyhE+F1cJAxA42W7duteFvrOBDyih6kSTUCyOFFHUwjRRlI1zyqquuio1+jzjiCENcuyw5AiLi5Lhk/aeOmPy0adNC2dabb77ZjB8/PnS+Ef7G0wRkecoppxiUvtwWliGfGuWTaDVqNmXKFKuKh/+8iITwe2opapjhr4g4ir3mks+OmPyGDRtcKjF3iiH8je3jkA3hb0SjoADmljE9QUhfFPL3kT2lf//+VtsXPPbZZx/DRqLvvvvOLTiyvhwRcdZ3cf4N/OSTT6y2b82aNfM/SUcKRIDwN5Kfon9AtuCrr77aML3ghpFHrUWLFqFNE4WCHKGHzuiXhc0xY8a40fScK0NEnHNdnrfBs2bNsrKMnTp1yntA79JGYOTIkYYfNYiJnHvoSRTFCPOirK5duxalGNevRYy/UaNGMQJm5yb60LLMERARZ45d1lzpiMmPHTs2a9oUZEPYERYf/samhUxzCY4ePdoSXtALXWyVj8/7dsABBxhElNgZKCs6AiLiomOYFSU4YvJMV8jcQQB9XKYqGNUS/sa8KaPcdA2tXZKnBrHoxUi3Xbt2sdEvKYjCuIiaLqZhO19EHLYeCcifb775xgbbH3jggQF5kL3VEktLKiewhZTbtGlj2DSSjtWqVcvO569fvz6dyzI+NzHvG4uHyiqSMZyFXigiLhSi3DmBXU6s1F9wwQW502ifW0p4lxP+RhJUph5S2eW4evVqS+KkWvLKvv/++zx535AN7d27t/n111+9qlLl/oOAiFi3Qh4EHDF55jVl3iGAIh4jY0bIZFJBa+KLL74osEJInPOJM3bTFi1aFFOio3x+IMiWLfMPARGxf1hHpiZHTF6Pot53GVMNLHohEE/4GyNeiDE/Y6MLsplEuxTV+NF18r5RZvv27SORQKCo7Q7j9SLiMPZKwD6xwk9IEuQg8w8BiNGRhCR+mBFwMiNTMTG7n332WbLDBX7G5p34vG81atQw/fr1M2zjlgWHgIg4OOxDXTOr5egDNGnSJNR+ZqNz6FigxMY0AVmpmYqI36XGD2WxYsXs1Eaq7V+wYIE577zzbJmUS78WNc451bp1XuEIiIgLxyhnz3DE5Jm/lPmPAHKY11xzjSVPVNnY2LFs2TLryOzZs+3nhSVYHTFihHHyvrH7j1C4FStW+N8Y1VggAiLiAuHRQVbNGUH997//FRgBIUBUBVKSbKKgLwglY47YEfpv0KCBTbrK3D6hckhMxud9Q+z+nnvuMWTEkIUTARFxOPslNF4xd+is7m/evDk0fuWqI1OnTjXMEUPIZLzmb/yrQoUKsfctW7Y006dPz1WoItVuEXGkuisYZ3kcPuaYY6ygfDAeqNZEBN56661YWqd4IuZ/VOEQtZdFBwERcXT6KlBPHTF5HnllwSNAgk0iJxJJmPfOPHLwXsqDVBEQEaeKlM6z84x80SFlWTAIxOfTS0bCdevWDcYx1VokBETERYIvty4mj5ojJr927drcanzArX3wwQetAD3kW7FiRbsYRxzxqFGjzKGHHmpHxii+eZlTL2AIsrp6EXFWd6/7jUNRjC2wfPll3iLw+eef58n7xiJdflvP3U7X5G3LVHoiAiLiRET0vlAEHDH5yy67rNBzdUL6CIBv48aN7Sh3l112sYtvaBzLshcBEXH29q2nLWNkxmMy6mEydxC4//77DemRwBUVvNtuu83VPHjueKlSvEBAROwFqjlSpiMm/9FHH+VIi91vJkL88XnfyAw9fPhw9ysyxpx77rmW5BMX+WbOnOlJfSo0dQRExKljpTMTEPj666+tmDybCGTpITBjxgw71w4plipVynTo0MHMnz8/vULSPLtq1aqW9Mn0Ef/atGlTmiXpdLcREBG7jWiOleeIyTPakhWMAFEnbDV2tiqjtMYWcrYke22QLaSv0a/XSGdWvog4M9x0VRwCjpj84MGD4z7Vvw4CTN3E531r1qyZ73PrjIAhYo1+nV4J118Rcbj6I7LeOGLyb7zxRmTb4Lbjzz77rCHZJgRYpkwZK/r+6quvul1NSuWh0sbUhCycCIiIw9kvkfNq48aNVkx+t912i5zvbjpMPC9C62RthoDRE7777rsNguxB2qmnnmq3RC9cuNDEv4L0SXX/DwER8f+w0H9FRMARk+dLn2u2fPlyG+8L+fI666yzQpV2nhG545vzNxf7Kaz3pYg4rD0TUb8cMflevXpFtAXpuU06IyfvG9EjhPS9/vrr6RXi8dkIBEG+zBPLwomAiDic/RJprxwxeQRqstEQX+/Tp4/Ze++9LcHVr1/fCreTwiiMRqQERKyFujD2zv/3SUQc3r6JrGcIyDti8r/88ktk25Ho+NKlS82FF14Ye8S/4IILzOTJkxNPC917Mj8jIi8LLwIi4vD2TaQ9c8Tks4EAJk6cGMv7VrlyZZs7DmH2qBhzwezek4UXARFxePsm8p45YvLXX3995Nry22+/mTvuuMPsvvvudgR84oknmiFDhpgojvCZlhg6dGjk+iCXHBYR51JvB9BWdpJBBFF4hAeed955J6bJULx4cdO2bVszbdq0AJBTlbmEgIg4l3o7gLb+/fffMTF5tCnCauPHjzdsOeZH4+CDDzY9evQwzAnLhIAfCIiI/UA5x+tATL5Ro0ZW2jFMUBBF0L17d8PIFwI+7bTTzCOPPGK2bNkSJjflSw4gICLOgU4OQxMdMfn27dsH7g7bsNlwAfmWLl3aIHCPfzIhEBQCIuKgkM/Beh0x+ZEjRwbS+jFjxsTyvh1xxBHmzjvvNOyIkwmBoBEQEQfdAzlWvyMmv2LFCl9aziaLbt262dEvI+DmzZsbCPnPP//0pX5VIgRSQUBEnApKOsc1BNhu27RpU1O2bFnXykxW0KJFiyzpQr777LOP6dy5s5k3b16yU/WZEAgcARFx4F2Qew44YvLM07ptaCNXqVLFjoDZTDJgwACzatUqt6tReULAVQRExK7CqcJSRYB5YkarAwcOTPWSfM9DYrJLly6x6YdWrVqZCRMmmB07duR7jQ4IgTAhICIOU29ksS+EihEeRryuY46YPNMImdiCBQvsNAeEvv/++5sbbrhBCmOZAKlrAkdARBx4F+SGAwjPQJjxue2+++47w+i1WLFiho0fqRqxvhUrVrTlNWjQwAwaNMisXr061ct1nhAIHQIi4tB1SfY55OjhQsKJYuSOmPxJJ51UYMNJsIlmBWTOCxW0qVOnFniNDgqBqCAgIo5KT0XYT5S/IGCEZ5JFSzBdUaJECdOwYUN7HoT72Wef2RaTYp4pDciXRTimM5QXL8I3g1xPioCIOCks+tAtBJzswfx1/k9WNoktndEuf0ntQ8YL/me0/PDDD5u1a9cmu1SfCYHIIyAijnwXhrsB8Vq4DhG///77eZxmhBtPws7/zP/OmDEjz7l6IwSyEQERcTb2akja5BAvc8SOQbJ8Hm9z5sxJSsRuhLbF16P/hUBYERARh7VnssCvxOkGZ6SbKFK+bds2U65cuX+R8ZIlS7IABTVBCBSOgIi4cIx0RgYIsADHPC+JKxkBOy92u911113/KpFRcZ06dSwZE5oWlDDQvxzTB0LABwRExD6AnGtVsHmjWrVqSQmXOeP4WOJEbNglJxMCuYaAiDjXetyH9jLiZTScLH07xxJjiX1wSVUIgVAjICIOdfdEzznIl1jhZNMPtIbPk8USR6+l8lgIuIeAiNg9LFWSMXYUzHxwstEwABFBkRg1IeCEQK4jICLO9TtA7RcCQiBwBETEgXeBHBACQiDXERAR5/odoPYLASEQOAIi4sC7QA4IASGQ6wiIiHP9DlD7hYAQCBwBEXHgXSAHhIAQyHUERMS5fgeo/UJACASOwP8Dvjad28jmU90AAAAASUVORK5CYII=[/img][br][br]The lengths of the sides of [math]DEF[/math] are shown. What is the length of [math]AB[/math]?
There is an angle ABC.
It is taken by a dilation with center [math]P[/math] and scale factor [math]\frac{1}{3}[/math] to angle [math]A'B'C'[/math]. The measure of angle [math]ABC[/math] is [math]21°[/math]. What is the measure of angle [math]A'B'C'[/math]?
Draw 2 lines that could be the image of line m by a dilation.
Label the lines [math]n[/math] and [math]p[/math].
Is it possible for polygon ABCDE to be dilated to figure VWXYZ?
[img]https://i.ibb.co/KGKw2c7/Geo-3-5-8.png[/img][br][br]Explain your reasoning.
Triangle XYZ is scaled and the image is X'Y'Z'.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAOEAAACjCAYAAAB8I3kdAAAWZUlEQVR4Ae1dC7BNVRh2e1CeRVK3hzxKM5JESlcppYcJIaZJhgklRpSo1NB7zGCUovTQbVJNNchVZnpT9C6lcW9IlBQ3UXNHymA138p/rbvPPmfvs89ae6+99//PnDl7r70e//rW/6219nrtWoKFEWAEIkWgVqSpc+KMACMgmIRsBIxAxAgwCSMuAE6eEWASsg0wAhEjwCSMuAA4eUaAScg2wAhEjACTMOIC4OQZASYh2wAjEDECTMKIC4CTZwSYhJptoHnz5mLKlCkZscKtUaNGYufOnRnP2CHdCDAJNZf/kCFDRLdu3WrEumrVKlGrVi2xaNGiGu58wwgAASahZjt47rnnJOHUaNu3by/69OmjOvE1I1CNAJOwGgo9F+huotVD6wfhbqgeXJMcC5PQQOmi5Zs5c6bYuHEjd0MN4Ju0KJmEBkp07NixsvuJd0O8I7IwArkQYBLmQifgMwzAoEuKkVIeDQ0IYoqCMQkNFDZ3Qw2AmuAomYQGCpdaQm4FDYCbwCiZhAYKFSOi6IqyMAJ+EGAS+kEpTz88IJMnYCn3ziQ0YACYmMekPQsj4AcBJqEflNgPI2AQASahQXA5akbADwJMQj8oBfBTXl4uFixYIDZt2hQgNAdJEwJMQgOlPW7cODlZjwl7/KZOnWogFY4yKQgwCTWX5LJly2oQkIjILaJmoBMUHZNQc2FOmzbNlYTomrIwAm4IMAndUCnA7c0333QlId4RWRgBNwSYhG6oFOjWpk2bGkTEOyILI5ANASZhNmQCun///feSgH379hX16tUT3bt3DxgTB0sLAkxCzSWN1TLFxcVi27Zt4oILLhDnnnuu5hQ4uqQhwCTUWKJLliyRreCsWbNkrCNGjBDNmjUTu3fv1pgKR5U0BJiEGku0bdu2oqSkpDrGGTNmSFLyoEw1JHzhggCT0AWUIE44UwZzgmVlZdXB33jjDem2dOnSaje+YAScCDAJnYgEuK+qqhK1a9cWgwYNqhH6hx9+kCScM2dODXe+YQRUBJiEKhoBr0eNGiUOPfRQsXr16owY0DpOnDgxw50dGAFCgElISAT8//rrr2Vrd/fdd7vGcOKJJ4qBAwe6PmNHRgAIMAkLtIMePXqI1q1bC3RJ3eSSSy4RnTt3dnvEboyARIBJWIAhvPLKK7IVfPrpp7PGMnr0aHHssceKPXv2ZPXDD9KNAJOwgPJv0aKFuPTSS3PG8Nhjj0mirlmzJqc/fpheBJiEAcv+oYcekuR65513csaA5xicwcJuFkbADQEmoRsqHm6VlZWSWMOHD/fwKcTPP/8s/c6ePdvTL3tIJwJMwgDlPnToUFG/fn2xfv16X6HREk6YMMGXX/aUPgSYhHmW+YoVK2TL9uCDD/oO2bJlSzFgwADf/tljuhBgEuZZ3l27dhXt2rUT+/bt8x2yZ8+e4pxzzvHtnz2mCwEmYR7lXVpaKlvB+fPn5xFKiFtvvVU0bdpU7N27N69w7DkdCDAJ8yhnbEvq1atXHiH+9zp37lxJXp6myBu6VARgEvosZixLwwAL3gnzleXLl8uw2FXBwgg4EWASOhFxuf/pp58kicaMGePy1Ntpy5YtMvzjjz/u7Zl9pA4BJqGPIscCbCw9A5mCSlFRkbj99tuDBudwCUaASehRuG+//bZsxbBLvhA5/fTTxTXXXFNIFBw2oQgwCT0K9uyzz9ayC+Lqq68WnTp18kiNH6cRASZhjlLHjngMxug4PfvOO+8UxxxzTI7U+FFaEWASZin5/fv3iwYNGmjbkIuPhoLQOJeUhRFQEWASqmgo15hgB2mwc16HfPLJJzI+HIvIwgioCDAJVTQOXFdUVEjC6DwbZuvWrTJO7C9kYQRUBJiEKhoHrrEqpnnz5uLPP/90eRrcqU6dOmL8+PHBI+CQiUSASego1sWLF8sWy8Qxhe3btxf9+/d3pMi3aUeASeiwAMzndevWzeGq5xaT/h07dtQTGceSGASYhEpRTp8+XbaCpk7Mnjx5smjSpImSIl8yAnzkYbUN7Nq1Sx7gO2TIkGo33RcvvfSSJPm6det0R83xxRgBbgkPFN5NN90kjjjiCKPzeJ999pkkIU9TxJgxBlRnEgoh5wIxJzhlyhQDEB+M8vfff5ckpE+nHXzCV2lGgEkohMAp2RiQCeOAXqzCue2229Jsc5x3BwKpJ+HLL78sWycsKwtDcNZMv379wkiK04gJAqkn4cknnyyuuOKK0Ipr8ODBAjszWBgBQiDVJLz//vtlK4jjJ8ISHJXYuHHjsJLjdGKAQGpJuH37dknAkSNHhlpMr732mkx3w4YNoabLidmLQGpJiG7h0UcfLTZv3hxq6Xz55ZeShKYWBISaGU5MCwKpJOHKlSslEaZOnaoFxHwi2bFjh0z70UcfzScY+00wAqkkYZcuXUSHDh0iK1bssMd+RRZGAAikjoTz5s2TLRE+8BmVlJSUiL59+0aVPKdrGQKpIyFaoagJMGzYsEhbYstsMPXqpIqEOGwJy9O++OKLSAt+2rRpclAoUiU4cWsQSA0J6WOdNryLLVy4UFYGGzdutMYQWJHoEIgNCVetWiUuuugiabxozU455RSxaNEi38jh4N3i4mLxxx9/+A5jyiPygjy89dZbppLgeGOEQCxIiBbjqKOOEtjrt3PnTgnvzJkzpSF/8MEHnnDTd+Nt2b2As2tAQlv08QQwQR5gP6jAbeqFxIKEIBqM1ik4hsLP9iOc7XL++ec7g0d6j1Z53LhxkeqQpMSpd4F/p6D8+/TpI52xUB+HeNkkmZZtk3YHdCGAnbUXwESLmEvwJSQQ2LbPknXv3l3gaHwWfQg0atQowx5QScOdelAgo5fN6NPIX0yxICGyAvDOOussgVYRZIQBo4YjcLNlt27duuK6667L9jgy95tvvlnmJzIFEpgwXleoxUP2qPJWxw5QcXvZTNjQxIaEAAYAo1XDTwU7G2i33HKLPDemvLw8m5fI3FEb4z2XRR8C6GrifY8ElbR6ZhAqcPWe/EX9HxsSjh07VnYrADR1MTBamq1WW7t2rSTrpEmTosbYNf3XX39d6oepExY9CKCHhAoa/7ARZ6sHN+crjZ6UC4slFiQE8dCvVwHENUDOVrP17NlTtGrVSvzzzz+FIWQo9OrVq6XBYOSWRR8CsAlU2CCjn5FzfSkHjykWJMQoqBvZsnXpysrKZCE888wzwZExHLKqqkrqyJ/Q1gs07AQEBBHjIrEgIYB1ewcE0Oj3O+XUU0+Vhzc53W27x/tLnIzFNvzc9KFXlWyvKW5honaLBQlpnvDee+8Vy5Ytk6NepaWlcmADXVVVsC4TNeH777+vOlt5jbNt3CoXK5WNiVKosE19xsAUBLEgITIPIsJg8W4IkgFoJwF3794tioqKBHYpxEEwWe/WksdBd1t1BJ5oDeMksSGhH1BHjBgh6tevLzZt2uTHe+R+sGwNlQqLHgTQBUUFrc4L6onZbCyJIeE333wjCwCnmcVFcBw+jOaXX36Ji8pW64nJefSQ4vQ+CEATQ0LMGZ5xxhlWG4lTuTVr1kgSxuH91ak73+tDIBEkxFEVaFFwmnac5O+//5Z6P/HEE3FSm3XVjEAiSHjCCSeIq666SjM04UR32mmn8W4KQ1Bj0T4+R1dZWWkoBT3Rxp6EdIo2PjsWR+ndu7fAj0UfAti43alTJ9nLQA8Jn7zDAg5bJdYkBNgAecyYMbbi66nX+PHjxZlnnunpjz34R+COO+6oJiDsAz/swLFVYk3CQYMGiaZNmwp89y+uMnv2bNGwYcO4qm+l3hdffHEGCUFEfI3ZRoktCT/++GMJtG0bNPMtZByHDwP57bff8g3K/rMgMHHixAwS2rwoIrYk7Ny5s8C3/uIuFRUV0mCwHI9FDwLoGdWuXbuaiIcddpjA1jFbJZYkxHI1tB6LFy+2FVffev3777/i8MMPF3PnzvUdhj3mRgC9I9jH8OHD5f+CBQtyB4j4aSxJiK8pDRgwIGLo9CXfrl07/oS2JjixWgYnFtDCeJDR9rWksSMhnaL93XffaSq26KPBmai9evWKXpEEaEAbemkDOG3ytTlrsSIh1liiZsMQdJIEAwloDVkKQwDEc7Z8WEtq+9amWJEQH3LBN+ZtHWoOakJYttagQYOgwTncAQSwfth5rgxaRvXwJxvBig0J33vvPVnLJXEAA8fhowbftm2bjTYSC52wfQkYOveY4n0Q7jaL3dopyGGHxIUXXqi4JOdy3bp10lA++uij5GQq5JygtXPrdtKpDG4nc4esYtbkYkHCOXPmSCNN6slke/fuFfXq1RM2H0yV1YIseECtndvpanQAsNszC1SXKsSChFiAO3ToUFswM6JHx44dxYQJE4zEneRIaUrC7TQ+yrdzsIbcbfm3noR4sa5Tp4748ccfbcHMiB7XXnst76YIgCzI5zyT1hlNrvNpnX6juLeahOvXr5fdUGxXSrrcddddsTsZIOoyofc9r8l426cprCYhjgRs06ZN1GUdSvpPPfWUPKQqlMQSkghNSXhlB70pm7/7YS0JsSsaffn58+d7YZyI5++++67M7/bt2xORH69MoPXCiCbKGD+QBOfK+hVaP+znZDVaS+o37rD9WUvCli1bCrSEaZENGzZIY1y5cmXis4wRS2wtApHoZDQilVfXEuAgTLYpCTfwqNtq6wiplSScMWOGNEjsGUyL7N+/XzRu3FjMmzcvLVnOyKff07NpSsLv3B8tZ/PTamYoFYKDdSTE1h50T0aNGhVC9u1KokuXLolbF5sPwtj54DbhrsYBQqHrmmtKQvVP17ApP60s+Q/z3zoS3njjjRLkrVu3homDFWnhi8JYH5tGofc2ry4jvtCMKQnqxvrFCt3ffInrN+5C/VlFwm+//Va2gtOnTy80X7EMf88994i2bdvGUvcgSmPUEgcwoZXCO55X95Le7YIcaWLzNIVVJMTa0A4dOgQpz0SEefbZZ+XytURkxkcmQDoQC6SiSXfnAmw1GhAWE+9BBF1RW6cprCHhq6++KmvEhQsXBsE4EWFwHD5ahR07diQiP/lmIhdRaPTUq7uaLU3q7mZ7HqW7NSQ8/vjjRf/+/aPEIvK08TUpkPDTTz+NXJcoFKDuJu2KJx1ofajXoA35d/unuIOS2C1OXW5WkPCBBx6QxocvK6VdjjvuOPH888+nEgaaenBmntyd5HT6y3Vv8zRF5CRELYfan3cQ/G9CXbt2FZMmTcplT7F/hq4hPpCKYwhx1CN+WC0DO3AOuhB5QMRCBfHriKdQPZzhIyfh9ddfL9AVraqqcuqWyvvBgwcnvluOARnMCWKQBcTA9AHu3bqKWB8aZErCzXhsnaaIlIR490Eh8KfBDprM5MmTeTfFATjoPS7XiOlB5LyvbJ2miJSEOEG7pKTEG70U+SgtLRV169ZNUY6zZxVzh2i9dAm6ojZOU0RGQgw+oBXEIUcsBxFYvny5xOWvv/466JjCK5pScOuiBoWD4gwa3lS4yEiIfj7ef1hqIrB582ZJws8//7zmgxTd0ZQEnaKtK+vUvdVJbB26RUJCjP4dcsghAjvnWTIROOmkk8QLL7yQ+SAlLljO5nVkRRAoaKTVtt0UoZPw119/lTW9jUPFQQrWRBgMIGAdaRoFI6cmpxJMxh20vEInIVbFtGrVSuzbty+ozokPh5PlBg4cmPh8umWQjqzId5eEW1xubjZOU4RKQuqTp3VFiJtRuLndd999WkcF3dKw0S3bKdo6dbVxmiJUEuIU7R49eujENJFx4X3wyCOPTGTecmUqnyMrcsWT65mN0xShkfDJJ5+UfX0+6j2Xifz/bMWKFRKrNK0iAjnwvmZ65JKmKUx1d71LN9NHaCTE12hHjhyZqQG7ZCCwZcsWaZBfffVVxrMkOmDUMsiRFUGwoFci02TPRzejJES3Cp8sxqoYfGsBxsXijcDq1avlEP1ll10mli5d6h0gpj7w7Y0bbrhB4BMADRs2zPvIiiDZxn5VtLjAFgvHbRBjJBw9erTMLDKMX5MmTVK7WTWfgsYJc0VFRTWwmzVrVj5RxMIvFmqQbeC/WbNmxkfMy8rKaqSJdF988cXI8TJCQhzSpAJM15dffrncsoJtK/xzxwBD6IQX/bdo0SJyQ9GpQHl5eUYekVeskDFpF61bt85I97zzztOZtUBxGSEhNueSAfH//z2BQnDA6qIkzavSMR6FYKIrbHFxcSDi6AxkhIRQELW3E6glS5bo1D2RcT388MMZuPXu3TtRecXZsjjo2GkfH374odF8YiOxM81hw4YZTdNP5MZIiA964mMuyDTecdK6DMtPITj94OQxMhacQJfEz8JhgIQ29eLTd6h8TMuePXtEv379qrG98sorQxkM8sqXMRJSwmvXrhW7du2iW/73iUBlZaXA0H3SpaKiQqBlDFOwfhm7VWwR4yS0JaOsByNgKwJMQltLhvVKDQJGSEgLcZ3dKVtWK0APOuWL/r2OYA/LImgrD70Tqv+FnLsZlv7OdGALJr4BAdt65JFHBI4DgeDeaW9OXXTfY0pFx95EIyREZvHSrR5fR7ulVTfdoPiNTzVsurbFwIETKgn1R+sqdRS4X4y8/FGF6jR8VCJYgkaHM8FQdZMQm35RbigzzKti6xfS0blHFfGRbTj/kXeUE9x1VN7GSAhA8O0AElv2cZHxkF62/8PIYdQwPNvEraLFTghVV9075Ok4fLVCIsKgbHUJyIX41B9sGD8I9NBVcRsjIYwHNQX+URNCeRtWrseNhMBNV2HrMlCKBxUtSEcCMqi6gijqPfkr5B/Ed7as1FMwaV9IQ61QkFdq7QvJD8IaIyEiRwGgNVSVL1ThQsODhNAnDgJjg9GZNK5CcKCKFq0GjNSpK1pE4K1LqAJ1dgGRDrVQutJS40FlggZFbX11pmeUhFRDqcqrmYviGjqh9sZ7BI5SwCoKermPQp9saVK3y2lw2fxH5Y4WgSpap666W0GyJ2deQQhn6+j0E/QeecLrANImQWWgc2zDGAnpXQatjk6FCYig/wAVgNIPtSh0VN9fg8atKxx0RM2rq7ujSy+3eFC20DWMMkaZOVsgah1NpI8eCOwCFY1JMUZCgAUDBzg2GbgbmGT0JgrSLb1cbij4sDa45tLDzzPoil4FSKi2FH7CBvGDNJAWCdKHncFNZ7eX4g9rLONgjihlDf+kPKJS3xs0RG0sCnSdwjAkrwxAD2dt7xUmqufQFa0EKi91gMaUPmRL+G49tjzR6KxKTF1pI0/oIaGCNi3aSYguFJQHYCTUKtK9jf/QMWoSUtcYNbztAqxoIIbIEYbBIg3ghPSRLn66u+3UxQ1rLEMrCQEQulJO5cOqKf0YrpuB0yCIiS6NH53gB5ihRqdaXt3cqtvI/OqUzR8ZqUq6OFS02fKjuoPUYc/LaiUh1VBqpnCNjKHrohaa009Y99AD76gYFYWh4xrGH/X7IGp26Ob2i1o3tWzISJ064R7GG3dBZYJ8qJUgXSPvJkQrCU0oqDtOtIQwGBg9/UyBq1t3G+JDRYufU2yqaJ26+b2nPLhVhHBz60X5jTuXv9SRMBcY/IwRiAIBJmEUqHOajICCAJNQAYMvGYEoEGASRoE6p8kIKAgwCRUw+JIRiAIBJmEUqHOajICCAJNQAYMvGYEoEGASRoE6p8kIKAj8B5nng0e++NHzAAAAAElFTkSuQmCC[/img][br][br]Write 2 equations that could be used to solve for [math]a[/math].
Lin is using the diagram to prove the statement, “If a parallelogram has one right angle, it is a rectangle.”
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAOAAAACYCAYAAAD9XOVNAAAN8klEQVR4Ae2dTUgWTxzHjYgoKKM3Kw0NCsIoO0REHTSwoJNvlVaC0rFDdgiik3nKl1KD6GpBUIfAqFOHUNDyJcJDFOXFTtEhsGtazZ/f9p/HfeaZfZ59dmZ2d3a/A8s+O7s7L5+dzzM7s49uCUMAARCIjEBJZDkjYxAAAQYB0QhAIEICEDBC+MgaBCAg2gAIREgAAkYIH1mDAAREGwCBCAlAwAjhI2sQgIBoAyAQIQEIGCF8ZA0CEBBtAAQiJKBFwNHRUVZXV5ezDA0NRVg1ZA0CxRNYXFzMacfUthsaGopPzMcZWgTs6upilZWVrLu7O2sZGxvzUQQcAgLxIUBttqSkJKsdU7seGRkxUkgtAtbW1rKOjg4jBUSiIBAmAZKttLQ0tCy1CEjfGKa+IUIjgYxAgDHnVtPU7aYMsLKAc3NzTpdNawQQsJ0AH0qFVQ9lAWmihXpAcRIGQoZ1CZGPLgILCwtOWx4eHmbj4+OZheJNBWUBaezHvzXckzCmCox0QcAUAZrNp85EXCjeVFAWsKamhtEsKAII2E6AOhDqTMIMygLSt4XJb4gwYSCvdBOIYjZfSUD+zMTkPXK6mwRqHyYB6kzC/vGIkoBhPzMJ82Igr3QR4LP5Yf94RElAel4iDlhpO+xKpKupoLYmCNBzbGq7YQelHOlbg2QTF/o9HQII2ESAhlFRdBxKAtoEGGUFgTgSgIBxvCooU+QElpaWQimDFgFv3rzJtm3bxtauXcsuX77Mfv/+HUrhkQkI6Cbw+PFjduDAAWc8ePLkSTY9Pa07i6z0lAUcGBjImYghCRFAwDYCfCbUPbG4Z88eo9VQFvD48eM5Aq5atYodPHiwqKW6uprRUux5OL44zuDlzausrCynLZOMr1+/NiahsoD19fU5hV69ejU7ffo0a29v970cOXLE+UF3MefgWP98wSo/q4sXL7Ly8vKctkwCvn37Nr4CPnr0KKfQGzdudOIaGxvZxMSEr8Lfu3ePvXjxwtexOAgEdBH49esXu337tjOHQbKtWbMmqz2fOHFCV1bSdJR7QEqVJNyxYwdbv349ozEhBfpJz+7du53KNDU1FRQRAkqvDyINEaBZTrd4Fy5cYO/evWOzs7OMD6voL31+/PhhqAT/ktUiICVFtzg0vhCDXxEhoEgO2yYIiOK1tbU54rnzevLkidNxfP361R1t5LNxAXmpC4kIATkprE0Q8CMezzeRAvLKeYkIATkhrHUSkIlHt5n5QqIF5BUXRaQ/6sUkDKeDtSqBIOLxPFMhIK8siVhRUeHccx87dqzgZA0/D2sQkBEg8Xp7ezOzmjTGK9TjiemkSkBe+ebmZrZlyxbfs6b8PKxBgAjoEI+TTKWAfAzo7hH9PL7g0LBOJwGd4nGCqRaQQ4CInATWMgImxOP5QEBOgjE2ODiYGSOiR3SBSelHLt727dud4UqQMV4hdBBQQkgUcXJyUnIUopJKIAzxODsIyElI1hBRAiXBUWGKxzFCQE4iz9otIs2gokfMA8vCXcvLy87jBJO3ml5YrBVw69at7Nq1a4EWerdEkAfxENGrGdkZL4rX2tpa9HM81ZpbK+C+ffvYhw8fAi8q4CCiCr3oz5WJNzMzE0nBrBVQ9tcQYROEiGETV8svTuLxmkBATkJhTSLyv3DGGFEBpKFTSby+vj7Gx3h0qxlVjydWEQKKRBS2IaICPAOnxlk8Xl0IyEloXENEjTADJGWDeLxaEJCTMLCGiAag5knSJvF4NSAgJ2FwfffuXYwRDfK1UTyOAwJyEiGsIaJeyFw8/j824zS54remENAvKY3HiSK+efNGY+rJTyoJ4vGrBAE5iQjWELE46EkSj9ccAnISEa7dIra0tDD0iNkXg17AQ8/xbL7VzK7RyhYEXGER+ae4iEj/tIp+L+teHj58GDofUbzz588bf4NQ2JWEgGET95Ff1CJWVlYy+k/N9BZX+m8B9Jn+lXpnZ6eP0qsfkgbxOCUIyEnEcB2FiPT6ZJJNfIUyiSiL14ktTeJxbhCQk4jxmkTctWuXI4DpMeLo6KiTz+LiYg6R0tJSRrenugOJ19/fnxnjJfFW04sZBPQiE8P4METs7u5mdAsqC7W1tYwWXSHN4nGGEJCTsGhtUkQSjMZ8skD7GhoaZLuKioN4K7gg4AoL6z6ZEJFuM2m8Jwu0j3rIoAHi5ZKDgLlMrIu5c+eOljEif2+5OAFDQCiOJmFojFhs4OLRex0pjTSN8QqxgoCFCFmy/+/fv0xVxJGREUcQWZXp9tNrbCg7nuIgnheZlXgIuMIiEZ9kIvp97zjNcMomWfhzQFnPKIMG8WRU5HEQUM7F+tggIpJ8jY2NbHx83FmGh4dZVVUVo7Gfn1tPiFd8s4GAxTOz6gxRxLNnzzKvHpHGZ3wh6UhImpCRPRN0Q/jz54/zHI+P8c6dO8empqbch+CzBwEI6AEmadHFiOi37hDPLynv4yCgN5tE7tEhIsTT1zQgoD6WVqXkR8TPnz+znz9/ZuoF8TIotH2AgNpQ2pkQF3Hnzp3O+I/GiA8ePGDV1dWZ8SDNjg4MDDCM8fRfYwion6mVKYoi8skY9xqTK/ovLQTUz9TqFD99+pTp+dzynTlzxup6xbXwEDCuVyaCctEYr6enRyrg/v37PR9fRFDUxGQJARNzKYNXhMSjMR4fB+7duzdLwnXr1mXeq5DvOWLwEqT3TAiY3mvPRPHcYzz6XWh7ezu7ceMGm5+fzzkWIuppOBBQD0erUsknXqGKiOeSiPjVSyFq3vshoDebxO0R5aEez+tnaYUqL6YFEQsRk++HgHIuiYqlRwzuMZ7O20dRRPdtbKIgGqoMBDQENg7JmhRPrB9EFIn424aA/jhZdVSY4olgIKJIJP82BMzPx6q9UYongoKIIhH5NgSUc7EqlsSjf0fBn+PpHOOpguAi4nekcpIQUM7Fitg4iycChIgikX/bEFDOJdaxNoknghT/bUXaZ00hoNhCYrxts3giVoj4jwgEFFtGDLe5ePz9EHEa46niSruIEFC1BRk8XyZeUl/emVYRIaBBgYImnSbxREYyEaenp8XDErMNAWN0KdMsnngZRBGT+u/sIaB45SPaVv238hEV23i2SRcRAhpvQvkzgHj5+fC9SRURAvIrHPIa4gUDnjQRIWCwdhD4LIgXGF3WiVzEsrIy599n2DpGhIBZl9XchomXaZorrT0pLy8vW/1+eQhouK1BPMOA/0+eROzr62O29YgQ0FD7gHiGwBZI1jYRIWCBC1rsbohXLDEzx9siIgTUdP1JvPLycmdCoKWlhU1OTmpKGcmoEIi7iBBQ5eoyxiCeIsCQTo+riBAwYANwi9fc3IweLyDHsE+TiTgzMxN2MTL5QcAMCn8fIJ4/TnE/ShSxtbWVRSEiBPTZUiCeT1CWHRa1iBCwQIOBeAUAJWR3VCJCQI8GBPE8wCQ8OmwRIaDQoCCeACSlm0tLS6y3tzfzWjZTY0QI+H8DGxwczDzHw6xmSq2TVNu0iKkXEOJJWh2icgiYEjG1AkK8nDaGCB8EdIuYOgFJvIqKCucnY3SrOTEx4QM7DgGBbAK6REyNgBAvuwFhSw8BVRETL6BbvKamJvR4etodUhEIBBUxsQJCPKGFYDMUAjIRZ2dnPfNOnIAQz/NaY0eIBEQR29ramExEKwU8deoUq6qqYvTKKx4gHieBdZwIFBKxv7/fmRCcmpoyXuwS1Ry+f//Ojh496hS4pKTEmc28evVqZlYTYzxVwjjfFAGZiI2NjZm2TO2ZfoVlMigLeOXKlawCU6FpoR6RuvL5+XksYBDrNvDx40d2/fp1tmHDBmlb/vbtmzEHlQU8dOiQtNBcRKz/fSGBg70cXr58GV8BL126lCMgjQWfPXuGBQysagM0dJJ9UX758iW+Ar5//55t3rw5q+BPnz41VmAkDAImCdTX12e1ZZLSZFC+BaXC0UTM/fv32cDAAKP7aQQQsJkAzV309PSwV69eGa+GFgGNlxIZgEBCCUDAhF5YVMsOAsoCjo2NsVu3bklrOzIywkZHR6X7EAkCcSYwNzfntGtq27Q8f/7cSHGVBezo6GC1tbXSwlVWVrLu7m7pPkSCQBwJLCwssLq6Omcihto1LTU1Nc42tXXdQVlAKlxXV1dOuRYXF51CUw+JAAI2ECD5Nm3a5AhHn92BtqlN6w7KAtJzE9ltJsXRPhOF1g0B6YEAEeC9XZhtVklA6t1IMvHbgipDt57UOyKAgA0EeIcR9h2bkoAkGQnIB6ruNf0axsQ9sw0XE2W0jwC1VZqzCDsoCdjQ0OAUmg9W3WsSc2hoKOz6ID8QCERANpdBHQxNyPAlUMIFTlIS0GuWk6ZwScCwu/MCdcVuEPAkQO1VnLGnx2gURx2Lqd4xsID5Zjmp4FQhBBCwhYBMQF52EtDUcCqwJXzQKpsxoscSVGgEELCFAN2C0q2mLJCcpoZTgQWkrtmrWyb5ZM8GZZVDHAjEgQAJRqLR3Zs78OEUrU2EwALm65ZlFTFReKQJAjoJ0KQitd3Dhw+zzs5Op0ek2XyKMxUCp0zfCLLnf1RQmnyR3ZqaqgTSBQFdBKhd090dX6hH9GrnOvIMLKCOzJEGCKSdAARMewtA/SMlAAEjxY/M004AAqa9BaD+kRKAgJHiR+ZpJwAB094CUP9ICUDASPEj87QTgIBpbwGof6QEIGCk+JF52glAwLS3ANQ/UgIQMFL8yDztBCBg2lsA6h8pAQgYKX5knnYCEDDtLQD1j5QABIwUPzJPO4H/AEgV4HpnPongAAAAAElFTkSuQmCC[/img][br][br]Given that [math]EFGH[/math] is a parallelogram and angle [math]HEF[/math] is a right angle, write a statement that will help prove angle [math]FGH[/math] is also a right angle.
[size=150]Han then states that the 2 triangles created by diagonal [math]EG[/math] must be congruent.[/size][br]Help Han write a proof that triangle [math]EHG[/math] is congruent to triangle [math]GFE[/math].[br]