Diagrama redusă
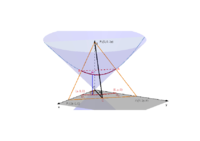
Această aplicaţie prezintă o porţiune a diagramei triunghiurilor izoperimetrice, cu perimetrul 2p.[br]În această diagramă [b]nu[/b] există două puncte p-triunghiulare corespunzătoare unor [i][b]triunghiuri oarecare congruente.[/b][/i][br]Punctul T(x,y,z) poate fi deplasat cu ajutorul mouse-lui. [br]În zona din dreapta ecranului se poate observa [math]\Delta XYZ[/math] corespunzător punctului T(x,y,z).[br]Caseta de sub triedrul drept, [i]Piramida[/i], permite vizualizarea/ascunderea:[br][list][*] tetraedrului punctelor p-triunghiulare, corespunzătoare triunghiurilor cu perimetrul mai mic sau egal cu [i]2p[/i],[/*][*] segmentului punctelor k*p-triunghiulare T[sub]k[/sub](x',y',z'), corespunzătoare triunghiurilor asemenea cu [math]\Delta XYZ[/math], cu raportul de asemănare subunitar, k. Punctul T[sub]k[/sub] (x',y',z') poate fi deplasat cu ajutorul mouse-lui. [math]\Delta X'Y'Z'[/math] poate fi vizualizat/ascuns cu ajutorul casetei [i]Triunghiuri asemenea.[/i][/*][/list][br][br]
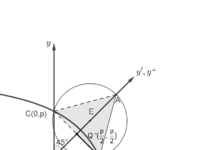
Determinaţi coordonatele punctului G, centrul de greutate al [math]\Delta XYZ[/math], în funcţie de coordonatele vârfurilor triunghiului.
Determinaţi coordonatele vârfurilor triunghiului X'Y'Z', dacă acesta are laturile respectiv paralele cu laturile triunghiului XZY şi acelaşi centru de greutate.