What is a line in Euclidean Geometry? It is the shortest distance between two points and it is straight and extends infinitely in both directions. [br][br]What about in spherical geometry?

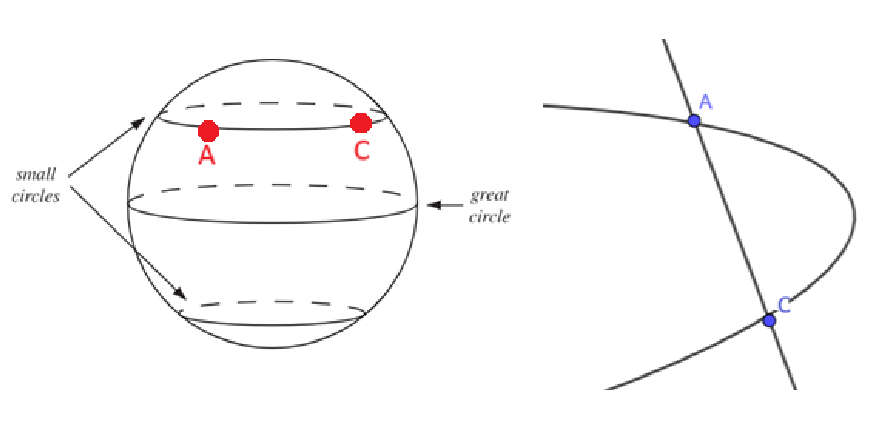
Lines in spherical geometry are defined as great circles which means that it passes through the center of the circle and you can visualize if I make a cut across this circle it would divide our sphere into two equal halves. [br][br]Why can't we just draw a smaller circle that would still connect points A and C?

Drawing a smaller circle connecting A and C would essentially be drawing another line that isn't the shortest path from AC as we can see from the image to the right. Instead we would want to reorient our sphere so that A and C directly lie on top of the great circle shown in the image and this would constitute a "line"

They don't exist! If we perform a cut along the center of an orange no matter how we cut they are going to intersect. Any cuts that don't intersect wouldn't satisfy the definition of a great circle.

Two Great Circles make up something called a lune in spherical geometry. The angle that the two great circles make we can call [math]\alpha[/math]. To get the area of the lune we can use some simple proportions. Since the area of the entire sphere is 4[math]\pi[/math][math]r^2[/math] and the fraction of the sphere that the lune occupies is [math]\frac{\alpha}{2\pi}[/math] we get [math]\frac{\alpha}{2\pi}\cdot4\pi r^2=2\alpha r^2[/math].

In euclidean geometry a triangle is characterized by three points that do not lie on the same line that are connected by straight line segments. [br][br]In spherical geometry we would have three points on the sphere but instead they are connected by great circles a triangle is 3 intersecting great circles. [br][br]Notice that because of the way that the lunes intersect, there will be not just one spherical triangle but two since there is another identical triangle that is on the opposite side of the sphere. To derive the area, we can try and write the area of the entire circle in terms of the lunes where L(angle) is the lune corresponding to the given interior angle of the triangle and T is the area of the spherical triangle. [br][br][math]2\left(L\left(\alpha\right)+L\left(\beta\right)+L\left(\gamma\right)\right)=4\pi r^2+4T[/math][br][math]2\left(2\alpha r^2+2\beta r^2+2\gamma r^2\right)=4\pi r^2+4T[/math] [br][math]T=r^2\left(\alpha+\beta+\gamma-\pi\right)[/math] [br][br][br]The special thing about spherical triangles is that they can have interior angles that sum up to more than 180. Looking at our example, each axis relative to the other is 90 degrees so we have three 90 degree angles which makes a total of 270 degrees. [br]

Question 1: What is the largest sum of interior angles we can get for a spherical triangle? [br]Question 2: Which of the following Euclidean isometries do you think are present in spherical geometry: translations, rotations, reflections, or glide reflections?

1. Airplane Navigation[br]-> Follow great circle routes which would otherwise be curved on a flat map. [br]2. GPS and Satellite Systems[br]-> Necessary for accuracy and positioning satellites [br]3. Map Projections[br]-> Spherical triangles help calculate true distances between points[br]