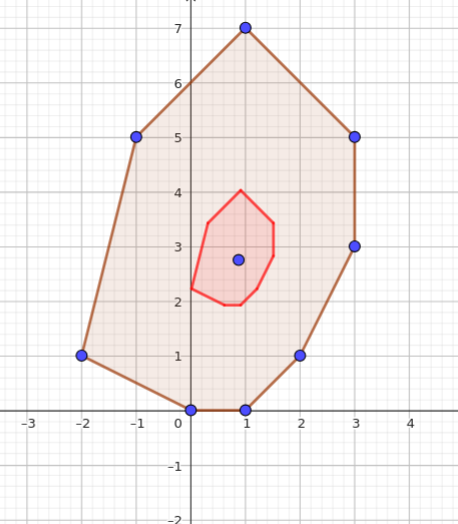
Image d'un polygone par une homothétie avec PyGGB
[url=https://www.geogebra.org/python/index.html?name=homoth%C3%A9tie&code=eJylUsFugkAQvfMVk%2FZQqCtFjWliwqWJTdpgbGJvxhgqo26FXbIsBs79mv5G%2B2OdBVHx1KYc4M0w8%2Fa9mb1%2BfoCx5igEQt%2Fr9nvwHoo9R0VRf2hdw1MSbhCim1xAKuNyI6kwDRXk9N3KROrt98fXJzFYVLxCoRVVI2xUuOfa%2FLrojUxuzQWvWOIQYp5phMA0ZZhBJpMEdeZaEa4PfDUX2oEzsoCeAnzwKlQe0Voq4MAFqFBs0I5RUPmhvukpoAPBnC%2Fc4pg2BGWTLqu0Qp0rAS%2BSC20XdzUTKxvAs%2BWeZ%2FwtRv9V5egY27yeUU4uqQkmtbWb1niMv8N4poDahCpMU6k07EaV2YrFnrAp2x2Et6Tsbu2JW3SnbuF06MWquKS4NHF5LuwxjDOjrC3tbwv4h4elOcsOzozM%2FPniV2uaucSHIrLrYZi1VDROex6VFXtWWxwXRt4q11wKGFEqoKXO66F5zHNYDXsn2Ge9Bg7Y4ASHp9r7BnZ7p3TXNC4sK6UDGhGBEcETv%2BX88t4yzx04VOWuZCyVf6UwuvoBi1IYkw%3D%3D]LIEN /LINK[/url]
[code][/code]#JB Etienne 20-21 janvier 2025[br]# Image d'un polygone par une homothétie[br][br]# centre de gravité d'un polygone défini par la liste L de ses sommets.[br]def centregravite(L):[br] x = 0[br] y = 0[br] for i in range(len(L)):[br] x = x + L[i].x[br] y = y + L[i].y[br] return Point(x/len(L),y/len(L),is_visible=True)[br][br]# image du point M par l'homothétie de centre O et de rapport k:[br]def image(M,O,k):[br] return Point(k*(M.x-O.x)+O.x,k*(M.y-O.y)+O.y,is_visible=False)[br][br][br]# image du polygone défini par la liste L de ses sommets par l'homothétie de centre O et de rapport k:[br]def image_poly(L,O,k):[br] S=[][br] for i in range(len(L)):[br] S.append(image(L[i],O,k))[br] return Polygon(S)[br][br][br]# Exécution :[br][br][br]L = [Point(0,0),Point(1,0),Point(2,1),Point(3,3),Point(3,5),Point(1,7),Point(-1,5),Point(-2,1)][br][br]p = Polygon(L)[br][br][br]im=image_poly(L,centregravite(L),0.3)[br]im.color="red"

