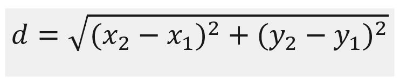
Coordinate Geometry Quiz
Distance Formula
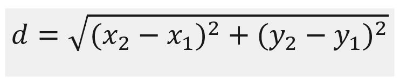
Midpoint Formula
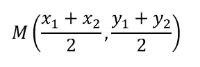
Slope Formula
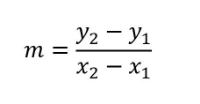
1
[b]Find [/b]the distance between the coordinates.[br][math]A(5,7)[/math] and [math]B(11,7)[/math].
2
[b]Prove [/b]that the points[math]A(0,0)[/math], [math]B(6,0)[/math] and [math]C(3,4)[/math]form an iscosceles triangle.
3
[right][/right]Point[math]A[/math] has coordinates ([math]1,2[/math]) and point [i][math]B[/math][/i] has coordinates ([math]5,8[/math]). [i][math]M[/math][/i] is the midpoint of[math]AB[/math]. [br][b]Find [/b]the coordinates of [i][math]M[/math].[/i]
4
[b]Find [/b]the coordinates where the line [math]2y-3x-7=0[/math] intersects the [math]y[/math]-axis.
5
[b]Find[/b] the equation of the line that passes the points [math]A(1,2)[/math]and [math]B(5,8)[/math].
6
The line [i][math]y=px+q[/math][/i] is parallel to the line [math]y=2x-6[/math]and passes through the point [math](-1,7)[/math]. [b]Find [/b][i][math]p[/math][/i] and [i][math]q[/math][/i].
7
a) Plot the points on the coordinate plane.

b)
[b]Justify [/b]that a linear relationship exists between [math]n[/math] and [math]C[/math].
c)
[b]Find [/b]the linear relationship in standard form.
d)
[b]Interpret [/b]what the gradient means in terms of [math]n[/math] and [math]C[/math].
e)
Interpret what the [math]y[/math]-intercept means in terms of [math]n[/math] and [math]C[/math].