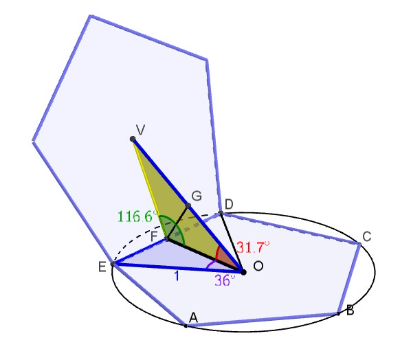
trigonomic calculation
distance between the centers of gravity of adjacent faces
[list][*]Create a regular pentagon inscribed in a circle with radius 1. [/*][*]In this pentagon [math]\left|FO\right|=cos\left(36°\right)=0.808[/math]. [/*][*]FOV is an isoscleles triangle with [math]\hat{F}=116.5651°[/math]. [/*][*]In this triangle [math]\left|OG\right|=.808\cdot cos\left(31.7°\right)=0.6875[/math] [/*][*]The distance between the centers of gravity O and V equals [math]\left|OV\right|=2\cdot\left|OG\right|=1.376[/math].[/*][/list]

distance bewteen the centers of gravity of faces connected to each other by one face
[list][*]In the dodecahedron [math]\left|OV\right|=\left|VW\right|=1.376[/math].[/*][*]The centers of gravity O, V and W form an isosceles triangle with [math]\hat{V}=108°[/math] and [math]\hat{W}=\hat{O}=36°[/math].[/*][*]In this triangle [math]\left|WF\right|=1.376\cdot cos\left(36°\right)=2.227[/math][/*][/list]
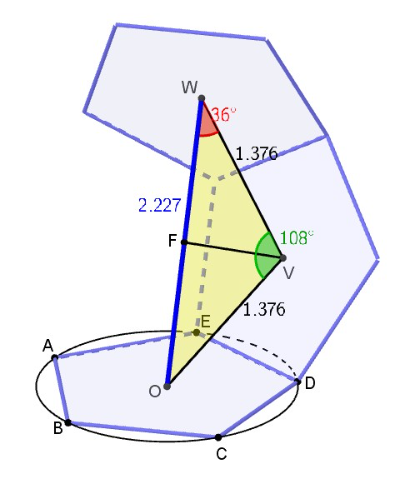
proportion of this two distances
The angle between [OV] and [VW] equals 108°, so [math]\hat{W}[/math]=36°.[br]The cosine of 36° equals [math]\frac{1+\sqrt{5}}{4}[/math] or [math]\frac{\phi}{2}[/math].[br]Since [math]\left|OW\right|=2\cdot\left|VW\right|\cdot cos\left(36°\right)[/math] you can also write [math]\left|OW\right|=\varPhi\cdot\left|OV\right|[/math].[br]Conclusion: the fascination of the admirers of the Golden Section for the fact that in a dodecahedron one can draw three Golden Rectangles perpendicular to each other can be reduced to a simple geometric property:[br][list][*]First define the centers of gravity of three faces: two adjacent faces and a third one, adjacend to the second face but not to the first one.[/*][*]Construct an angle with vertex the center of gravity of the first face and legs the segments that connect this point to the other two points.[/*][*]Constatation: The constructed angle in the center of gravity of the first face equals 36°.[/*][/list]