Funciones reales
Antes de comenzar con la lección, les pido que observemos el siguiente video sobre las funciones.
1.1 Notación de funciones
Problema inicial: Encuentra el valor de[math]y[/math]correspondiente al valor de[math]x[/math]en cada una de las funciones si: a)[math]y=5x-1;x=-3[/math] b)[math]y=4x^2;x=\frac{1}{2}[/math] c) [math]y=\frac{x^2}{2}+5;x=10[/math]
Solución:
Definición:
Se define la función de A en B, a la correspondencia que asigna a cada elemento [math]x[/math] del conjunto A, un único elemento [math]y[/math] del conjunto B. Para denotar una función de A en B se escribe:[br]f: A -- B, al elemento [math]x[/math] de A se le llama variable independiente o preimagen; mientras que el elemento [math]y[/math]d B se llama variable dependiente o imagen.[br][br]Se denota y como f(x) y se lee "f de x", para un valor [math]x=m[/math] al encontrar el valor de [math]f\left(m\right)[/math] se sustituye [math]x[/math] por [math]m[/math] en la ecuación de la función [math]f[/math].
Ejemplo: Dar clic sobre cada icono para visualizar el proceso realizado.
Ejercicios: Los que aparecen sombreados en la imagen.

1.2 Gráfico de una función
Ddas las funciones [math]f\left(x\right)=-2x[/math] y [math]g\left(x\right)=2x^2[/math].[br][list=1][*]Elabora la gráfica de cada una de ellas.[/*][*]Traza las lineas rectas verticales en cada gráfica. ¿Cuántas veces cortan las rectas verticales a las gráficas de [math]f[/math] y [math]g[/math]?[/*][*]Si se continua trazando rectas verticales, ¿Cuántas veces cortarán a la gráficas de las funciones [math]f[/math] y [math]g[/math]?[/*][/list]
Solución: Dar clic en los botones que aparecen.
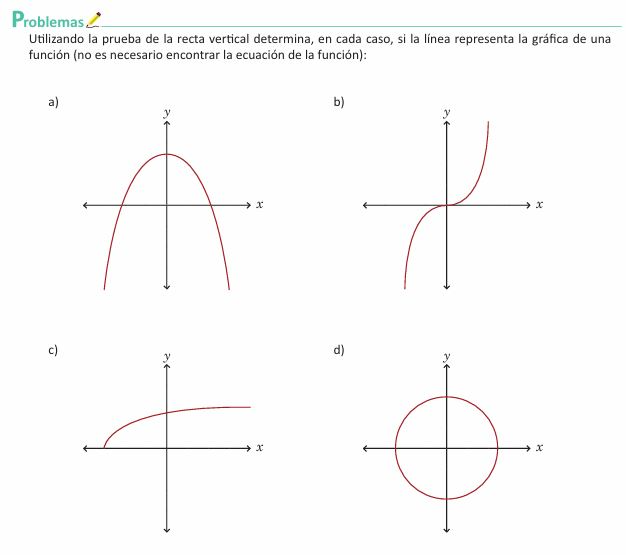
Conclusión
Una linea trazada en el plano cartesiando, cuyos valores de [math]x[/math] se encuentran en un intervalo [math]I[/math], corresponde a la gráfica de una función si toda recta vertical trazada en el intervalo [math]I[/math] corta a la línea en un único punto. A esta manera de reconocer gráficas de funciones se le conoce como [b]prueba de la recta vertical.[br][/b]Esto ocurre debido a la definición misma de función, ya que a cada elemento de x le corrresponde un único elemento de y. Las rectas trazadas en cada gráfica representan un valor específico para x, si esta recta corta a la gráfica de una función en un único punto, entonces esto indica que para ese valor de x hay un único valor para f(x) o g(x).
Ejercicios: Resolver todos los problemas.