Rectas y planos en el espacio
En el plano se usa la pendiente para determinar una ecuación de una recta.[br]En el espacio es más conveniente usar vectores para determinar la ecuación de una recta.[br][br][br][br]
Rectas y planos en el espacio.
En el plano se usa la pendiente para determinar una ecuación[br]de una recta.[br]En el espacio es más conveniente usar vectores para determinar la ecuación de una recta.[br][b]Ecuación vectorial[/b][br]Dados un vector ⃗V=(V1,V2,V3)y un punto P0(Xo,Yo,Zo), nos proponemos hallar la ecuación de la recta[b] r[/b] que pasa por el punto Po y es paralela al vector ⃗v.[br]Consideremos un punto P(x,y,z) perteneciente a la recta [i]r[/i]. El vector ⃗ PoP resultará paralelo al vector director ⃗v[br][br]⃗PoP=α⃗v[br][br](x–x0,y–y0,z–z0)=α(v1,v2,v3)[br][br](x,y,z)=(x0,y0,z0)+α(v1,v2,v3),α∈R Ecuación vectorial de la recta[br][br][list][*]Un vector (U ) que le de la dirección.[b] [/b][/*][*]Un punto (P0) que la fije en el espacio[/*][/list][br][br]


Ecuación Implícita
[br][br]Una recta puede venir determinada por la intersección de los planos[br]⌈Ax+By+Cz+D=0[br]⌊A ʼx+B ʼy+C ʼz+D ʼ=0 [br]Si en las ecuaciones continuas de la recta quitamos denominadores y pasamos todo al primer miembro, obtenemos también las ecuaciones implícitas[br][br]



Ecuación simétrica de la recta
[br]Si v1,v2,v3v1,v2,v3 son distintos de cero, entonces:[br][br]α=x–xo/v1,[br][br]α=y–yo/v2,[br][br]α=z–zo/v3[br]Igualando, resulta:[br][br]x–xo/v1 = y–yo/v2 =z–zo/v3 = Ecuaciones simétricas de la recta[br][br][br]


Funciones de dos variables
[justify]Una funcionalidad de 2 cambiantes es una regla de correspondencia que asigna a cada pareja de números reales (x, y) un y únicamente un número real z.[br][br][b]Dominio[/b][br]El grupo de parejas ordenadas para las cuales la regla de correspondencia da un número real se denomina dominio de la funcionalidad. El grupo de valores z correspondientes a los pares ordenados se denomina contra dominio.[br][br]Una funcionalidad de 2 cambiantes se denota comúnmente con la notación z = f (x, y).[br][br]Las cambiantes x, y se denominan cambiantes independientes, y z se denomina variable dependiente.[br][br]La gráfica de una funcionalidad de 2 cambiantes es el grupo de aspectos con coordenadas (x, y, z) en donde (x, y) está en el dominio de f y z = f (x, y).[br][br]Este grupo de aspectos forma una área en el espacio tridimensional.[br][br]La gráfica de una funcionalidad de 2 cambiantes es el grupo de puntos de vista con coordenadas (x, y, z) en donde (x, y) está en el dominio de f y z = f (x, y).[br][br]Este grupo de puntos de vista forma una área en el espacio tridimensional. [br][img]https://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/image001.gif[/img][img]https://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/image002.gif[/img][br]Figura 1 Espacio Tridimensional Rescatado de M.F.M. (2009). Monografias.com. https://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml[br][br]De manera, la gráfica de una funcionalidad f de 2 cambiantes es una área que consta de todos los puntos de vista del espacio tridimensional cuyas coordenadas cartesianas permanecen determinadas por las ternas ordenadas de números reales (x, y, z). Como el dominio de f es un grupo de puntos de vista del plano x, y, y pues cada par ordenado (x, y) del dominio de f corresponde a solo un costo de z, ni una recta perpendicular al plano x, y puede intersectar a la gráfica de f en más de un punto. [/justify][br][b]Ejemplos:[/b][br][br][b]Dominio de las funciones de dos variables [/b] [br][br]
1. f(x,y)= 4√y-2x : y-2x ≥ 0 : Dom= y ≥2x
2. g(x,y)=xy √ x^2 +y : x^2 +y ≥ 0 : Dom=y≥-x^2
3. h(x,y) = x^2+y^2 / : x-y x-y # 0 : x-y = 0 : Dom= R^2 -[(x-y)(x=y)]
Superficies Cuadráticas
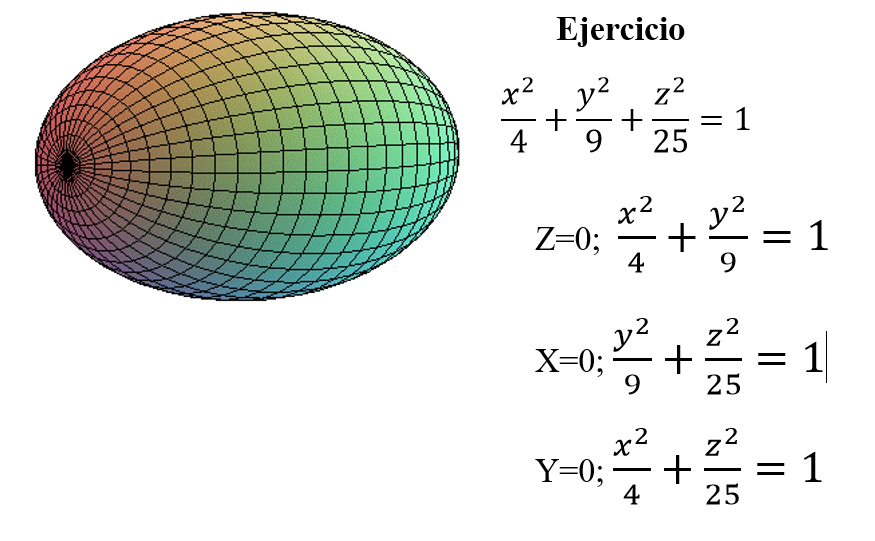
Una superficie cuadrática es la gráfica de una ecuación de segundo grado en tres variables x,y,z.[br][br][b]Elipsoide: [/b]todas las trazas son elipses. Si a=b=c, la elipsoide es una esfera.[br]
[b]Paraboloide elíptico: [/b]las trazas horizontales son elipses. Las trazas verticales son parábolas. La variable elevada a la primera potencia indica el eje del paraboloide.[br]
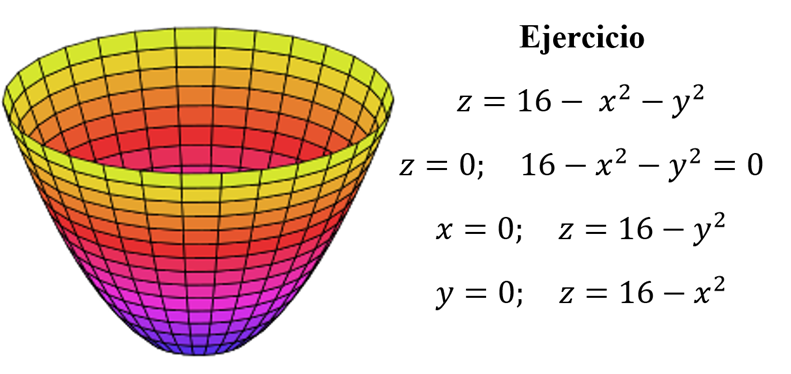
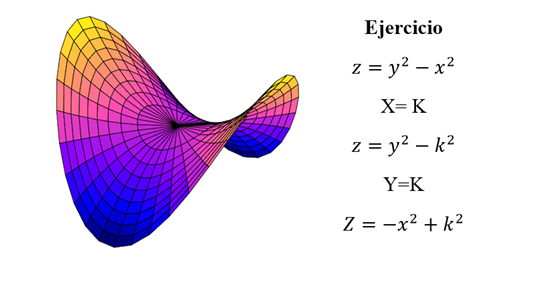
[b]Paraboloide hiperbólico: [/b]las trazas horizontales son hipérbolas. Las trazas verticales son parábolas. Se ilustra el caso donde c<0[br][br][br]
Parametrización de curvas
[justify]Consideramos una curva en el plano como una línea trazada sobre un papel, tal como puede ser una línea recta, una curva parabólica o una circunferencia.[br]Este par de ecuaciones, que muchas veces es una forma conveniente para describir una curva, se llama ecuaciones paramétricas de la curva en el plano: [/justify][center]x = f(t)[br][/center][center]y = g(t)[/center][justify][size=100][/size]Cada valor de t determina un punto (x, y) en el plano. Cuando t varía (en un intervalo de números reales), el punto (x, y) = (f(t), g(t)) se mueve generando una curva en el plano.[size=100][br][/size][/justify]


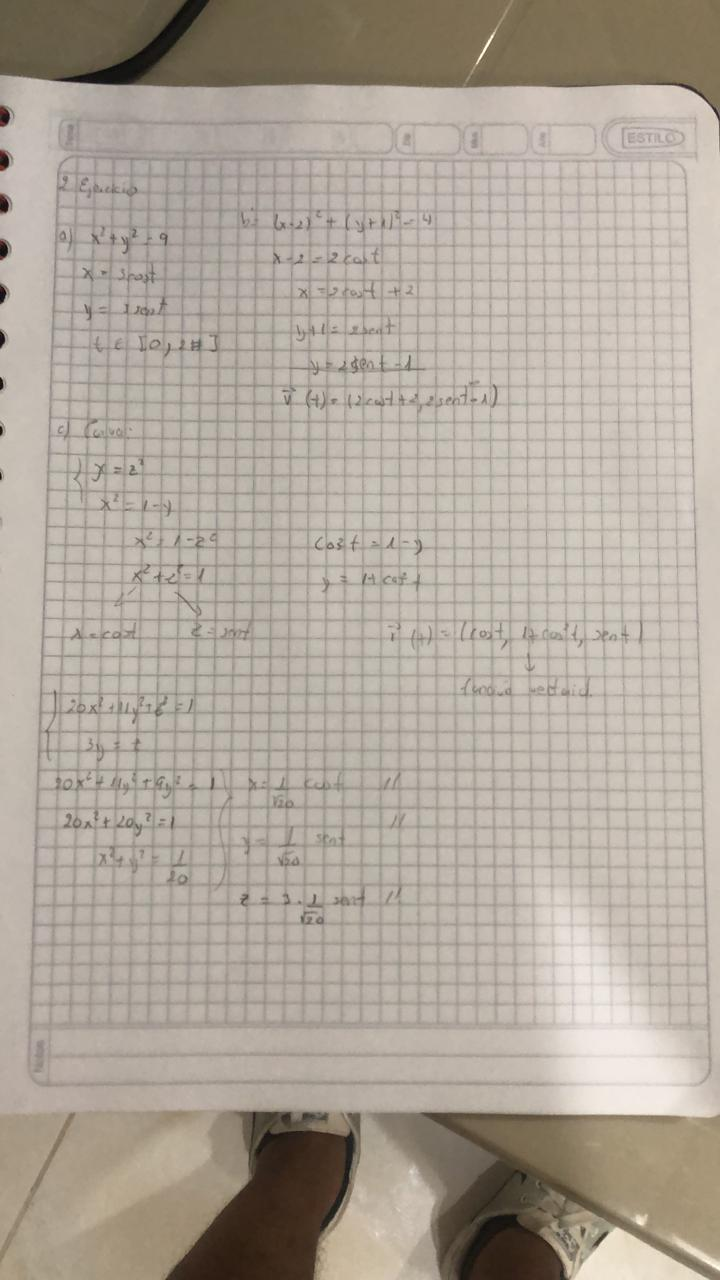
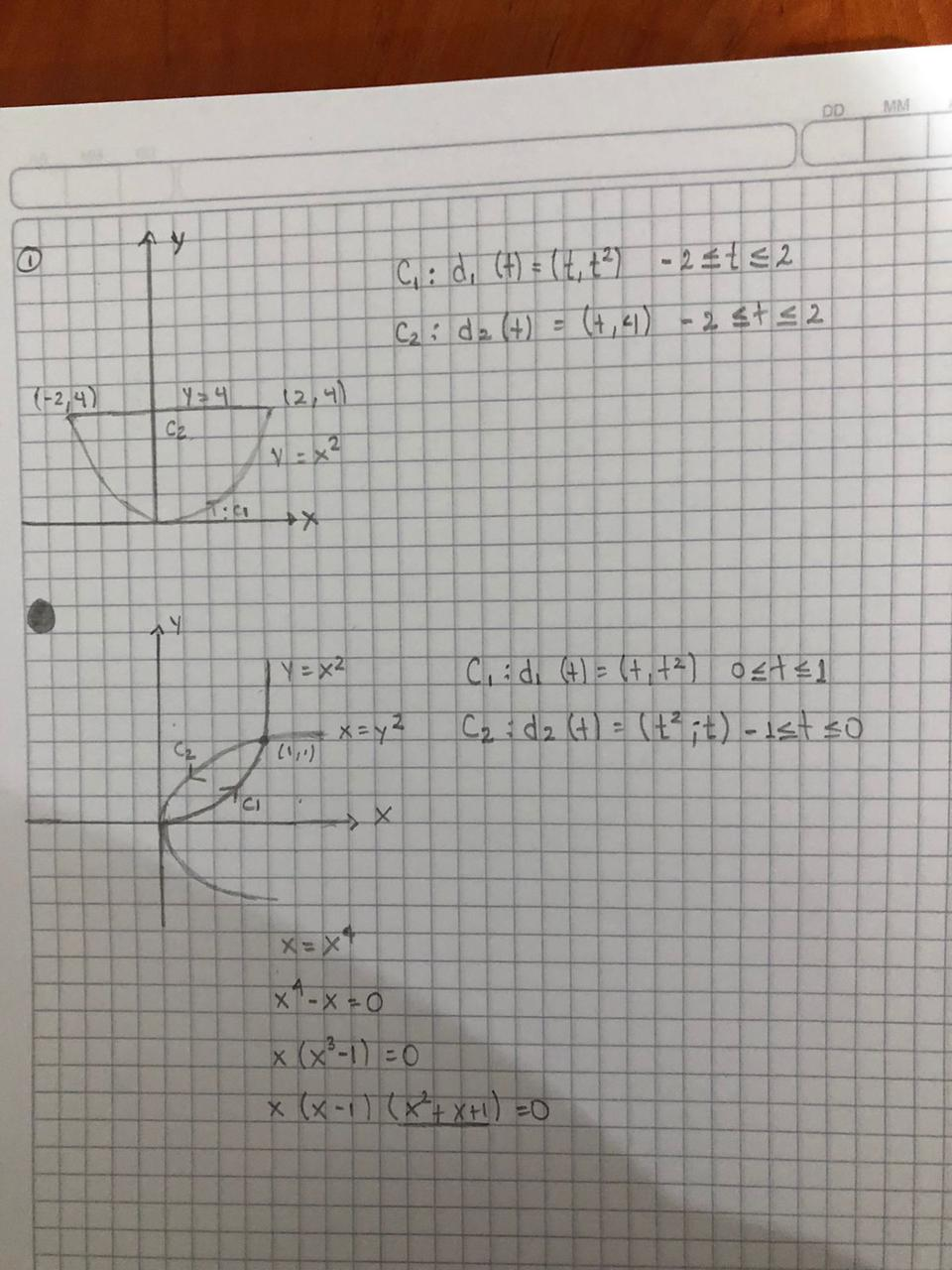
Funciones vectoriales de un parámetro
[justify]Una función con valores vectoriales es una función cuyo rango o imagen es un conjunto de vectores ~r (t), cuyo dominio está en la recta real (intervalo I, cerrado o semicerrado, o toda la recta) y cuyo rango o imagen está formado por vectores del espacio o del plano. Se tiene :~r: I ⊂ R → Vn[br]donde n = 3 ´o 2[br]Una función vectorial de un parámetro representa una región del plano o del espacio que no es una región solida ni una superficie, sino que podríamos decir que es un “objeto unidimensional”: ~r(t) representa una curva paramétrica en el espacio o en el plano coordenado.[br][br]Ejemplo[br]El movimiento de una partícula en el plano está definido por la siguiente función vectorial: ~r1(t) = (4 cost, 4 sen t), 0 ≤ t≤ 2π Graficar la curva imaginaria que describe la partícula al moverse, indicando los puntos iniciales y final, así como el sentido del recorrido. b). Si el movimiento está representado por ~r2(t) = (−4 sen(2t), 4 cos(2t)), con 0≤ t ≤ 2π, ¿cuál es la curva determinada?[br][br]a) Las funciones componentes son x1(t) = 4 cost e y1(t) = 4 sen t. Si para algunos valores de t situamos en el plano los puntos P(x1(t), y1(t)), o sea P (4 cost, 4 sen t), su ubicación parece indicarnos que la curva es una circunferencia (evalúe ~r1(t) en t = π 4 , π 2 , π, 3π 2 ). Si eliminamos el parámetro t entre las ecuaciones x = x1(t), y = y1(t), obtenemos la ecuación cartesiana de la curva. Para ello, en este caso conviene sumar las componentes al cuadrado para eliminar el parámetro, entonces queda: x 2 + y 2 = [x1(t)]2 + [y1(t)]2 = (4 cost) 2 + (4 sen t) 2 =16 cos2 t + 16 sen2 t = 16(cos2 t + sen2 t) = 16 luego x 2 + y 2 = 42 .[/justify][br][br][br][br][br][br]
Funciones Vectoriales
Una funcionalidad vectorial es aquella cuyo dominio es un grupo de números reales y cuyo rango es un grupo de vectores. Esto significa que tenemos la posibilidad de conceptualizar la funcionalidad como: [br] [br]r(t)=(f(t),g(t),,h(t))=f(t)[math]i^{\rightarrow}[/math]+g(t)[math]j^{\rightarrow}[/math]+h(t)[math]k^{\rightarrow}[/math]
Derivada de funciones vectoriales.
Si r(t ) =(f (t ),g (t ),h (t ))= f(t )i +g(t )j +h(t )k donde son funciones derivables entonces:[br][br]r′(t) = (ƒ[sup]′[/sup](t), g[sup]′[/sup](t), ℎ[sup]′[/sup](t)) =ƒ′(t) i+ g′(t) j + ℎ′(t) k[br][br]1. Ejemplo:[br]Calcule la derivada de r(t)=(1+ t[sup]3[/sup]) i +t e[sup]−t [/sup]j+ sen(2)t k[br]R= Se deriva cada componente de r: r[sup]′[/sup](t)=3t[sup]2 [/sup]i+(1−t)e[sup]−t [/sup]j+2cos2t k[br][br][b]OJO:[/b][br]Al vector r′(t) se le denomina vector tangente a la curva descrita por la curva C: r(t) en el punto P siempre que r′(t) exista y r′(t) ≠ 0[br]La recta tangente a C: r(t) en el punto P se define como la recta que pasa por P y que es paralela al vector tangente r′(t).[br]El vector unitario tangente es: T(t) = r′(t)/|r′(t)|[br]Al igual que las funciones de valores reales la segunda derivada de una función vectorial r es la derivada de r′ es decir r′′ = (r′)′[br][br]2. Ejemplo:[br]Determine las ecuaciones paramétricas de la recta tangente a la hélice de ecuaciones paramétricas[br] x=2cos t y=sen t z= t en el punto (0,1,pi/2)[br]La ecuación vectorial de la hélice es r(t)= (2cos t, sen t, t) de modo que r´(t)=(-2sen t, cos t, 1)[br]El valor del parámetro que corresponde al punto (0,1, pi/2) es t= pi/2 de modo que el vector tangente es r´( pi/2)=(-2,0,1)[br][br]La recta tangente es la recta que pasa por (0,1, pi/2) y es paralela al vector (−2,0,1) de modo que sus ecuaciones paramétricas son[br][br]x=-2t y=1 z=pi/2[br][br]
Integrales de funciones Vectoriales
Si r(t)=(f(t),g(t),h(t))=f(t)i+g(t)j+h(t)k donde son funciones integrables entonces[br][math]\int_a^br\left(t\right)dt=\int_a^bf\left(t\right)dti+\int_a^bg\left(t\right)dtj+\int_a^bh\left(t\right)dtk[/math][br][br]Ejemplo:[br]Calcule la integral de r(t)= (2cos t)i+ sent j+ 2t k) en el intervalo [0, pi/2][br]Se integra cada componente de r:[br][math]\int_0^{\frac{pi}{2}}r\left(t\right)dt=\int_0^{\frac{pi}{2}}2costdti+\int_0^{\frac{pi}{2}}sentdtj+\int_0^{\frac{pi}{2}}2tdtk[/math][br][math]\int_0^{\frac{\pi}{2}}r\left(t\right)dt=2senti-costj+t^2k|_0^{\pi}=2i+j+\frac{\pi^2}{4}k[/math]