hamiltongrafen
hamiltongrafen binnen de grafentheorie
Table of Contents
- Hamilton
- twaalfvlak als planaire graaf
- Schlegel diagram twaalfvlak
- hamiltongraaf - een reis rond de wereld
- Probeer het zelf
- creëer een hamiltoncykel op graaf en dodecaëder
- paardenrondgang
- het paard in het schaakspel
- planaire graaf
- een paardenrondgang
- eenvoudige woordpuzzel
- Seneca
- meer puzzels
- oplossing
twaalfvlak als planaire graaf
Leonardo da Vinci (1452-1519)
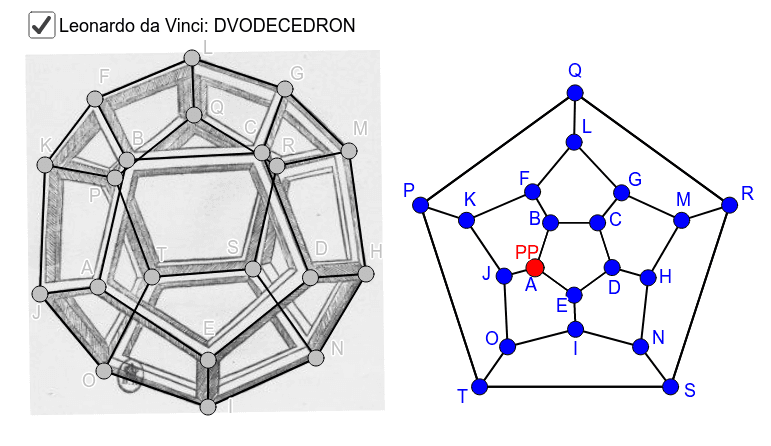
Leonardo da Vinci maakte in 1509 tekeningen van ruimtelichamen voor het boek van Luca Pacioli [i]De Goddelijke Verhouding[/i].[br]In dit boek vind je de eerste tekeningen van veelvlakken ooit als een raamwerk van ribben, zodat je door de structuur kunt kijken. Het is echter niet duidelijk of Leonardo deze vorm zelf bedacht dan wel of hij de tekeningen maakte naar houten modellen die Pacioli ontwierp.[br]Een van de afgebeelde veelvlakken is het [b]twaalfvlak of dodecaëder [/b]met12 regelmatige vijfhoeken als zijvlakken.
versleep de grijze punten
Versleep de grijze punten van het twaalfvlak naar rechts zodat de overeenkomende punten kloppen.
Het twaalfvlak is een van de 5 Platonische lichamen. Deze lichamen hebben congruente hoekpunten, zijvlakken, ribben en hoeken.[br]In de planaire graaf zie je duidelijk dat een twaalfvlak 20 hoekpunten heeft, 30 ribben en 12 zijvlakken.[br]Dit volgt uit de [b]formule van Euler[/b]. [br]In een veelvlak met h hoekpunten, r ribben en z zijvlakken geldt steeds h - r + z = 2.[br]Voor een twaalfvlak krijgen we 20 - 30 + 12 = 2.[br]Het Schlegeldiagram, de afbeelding van een twaalfvlak als een planaire graaf, geeft een duidelijk inzicht in de onderlinge structuur van hoekpunten en ribben.[br]Je kunt ook van de andere platonische lichamen dergelijke planaire voorstellingen maken. Je leest er meer over in het boek [url=https://www.geogebra.org/m/jbmpxu36]Ruimtelichamen, grafen en paden[/url].[br]
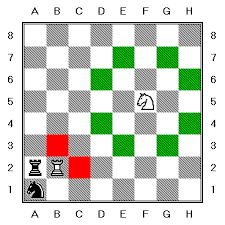
het paard in het schaakspel
het paard
In het schaakspel is het paard een apart stuk. Waar andere stukken rechtdoor of diagonaal bewegen, heeft de paardensprong een L-vorm: Je verplaatst een paard ofwel 2 velden horizontaal en 1 veld verticaal ofwel 2 velden verticaal en 1 veld horizontaal.
alternatieve borden en puzzels
Je kunt alternatieve schaakborden bedenken en bijgaand puzzels bedenken.[br][list][*]Vanuit welk vak kan je welke vakken bereiken met een paardensprong?[/*][*]Kan je een paardenrondgang bedenken? [br]M.a.w.: kan je vertrekkend vanuit bv. vak 1 met paardensprongen achtereenvolgens alle vakken aandoen en terug eindigen op 1?[/*][/list]Het kan helpen om alle mogelijke verbindignen af te beelden op een graaf. [br]Bekijk alle mogelijke paardensprongen in volgend applet.[br]Met [b]Knight's Tour[/b] als zoekterm vind je tal van sites en puzzels. [br]Zie bv. ook [url=https://en.wikipedia.org/wiki/Knight%27s_tour]Knight's tour[/url] op Wikipedia of [url=https://bradfieldcs.com/algos/graphs/knights-tour/]A Knight's Tour[/url] waarin ook een Python oplossing van het probleem beschreven wordt.