Fostering the competence Reasoning and Proof
Fostering the competence Reasoning and Proof across the grades by GeoGebra The Austrian educational standards for Mathematics (IDM, 2007) at grade 8 define competences such as “cognitive abilities which are available for a longer time (and the readiness to make use of them)”. Moreover, they define four content areas and four types of mathematical activities/processes. One of these activities is, as with many other mathematical standards Reasoning and Proof. To be able to reason and prove requires continuing development. Extending the spiral curriculum with its main ideas (revisiting topics, increasing complexity) to typical mathematical activities enables a step-by-step acquirement of competence (cf. Süss-Stepancik & Götz, 2015). But what is the specific part of GeoGebra in this stepwise process? First of all GeoGebra supports the disposition to engage in mathematical tasks that demand reasoning. Secondly GeoGebra fosters the ability to understand, comprehend and explain prescribed reasons. Thirdly GeoGebra can also foster the ability to explain and argue a completed mathematical proof. And in the end GeoGebra supports the finding of reasons for a (mathematical) statement/conjecture autonomously. The four steps named above will be clarified with the content of the surface area, which leads from grade 5 to grade 12.
Table of Contents
- Austrian math standards at grade 8
- The three-dimensional model of competence
- Spiral curriculum
- Spiral Curriculum (J. Bruner)
- A competence based four level model for arguing
- Four level model for arguing
- Area surfaces
- Surface Area - Trapezoid
- Surface area - Circle
- Integral calculus - determining areas
- Summary
- Summary
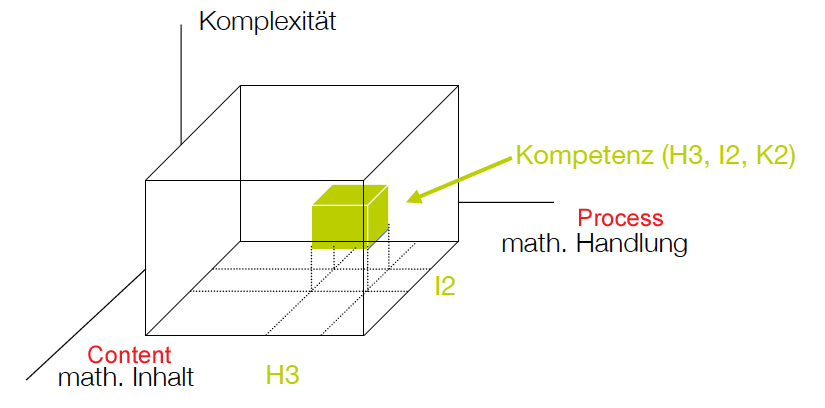
The three-dimensional model of competence
In Austrians maths lessons the topic [i]Reasoning and Proof[/i] is very important from grade 5 to grade 12. For this grades we have two different competence models. One for grade 8 and one grade 12. The model at grade 8 is a three-dimensional model (see below). One of these three dimensions is equal to the [b]Process standards[/b] and includes [b]Reasoning and Proof[/b].[br]The second dimension is equal to the [b]Content standards[/b] and contains [b][i]Numbers and Measurement[/i][/b], [b][i]Algebra and functions[/i][/b], [i][b]Geometry[/b] [/i]and [i][b]Data analysis[/b][/i]. The third dimension describes the [b]complexity[/b] that students have to manage. [br]
Process - Content - Complexity
Competences are defined as ...
"[i][size=150]cognitive abilities which are available for a longer time and the readiness to make use of them[/size][/i]"[br][br]The competence model at grade 12 is only one-dimensional and describes 73 competences combining the content and the process. In this model only two competences refer to “reasoning and proof”. So for the final exam for the general qualification for university entrance „reasoning and proof“ seems not very important, but for the math lessons at secondary school reasoning and proof plays still an important roll.[br][br]bifie (Hrsg.) (2011): Praxishandbuch für „Mathematik“ 8. Schulstufe. Graz: Leykam.[br]IDM (2007): Standards für die mathematischen Fähigkeiten österreichischer Schülerinnen und Schüler am Ende der 8. Schulstufe.
Spiral Curriculum (J. Bruner)
As we know, it is very hard for students to find reasons and proofs by their own. We are sure that reasoning and proof requires [b]continuing development[/b]. One – very old – concept that deals with continuing development is the [b]“Spiral curriculum”[/b] by Jerome Bruner.
Key features of the spiral curriculum
[size=150]*) revisiting a topic, theme or subject[br]*) complexity increases with each visit[br]*) new information are put in context with old information[/size]
Benefits of the spiral curriculum
[size=150]*) information is reinforced an solidified[br]*) progression from simplistic to complicated ideas[br]*) apply early knowledge for later course objectives [/size]
Spiral Curriculum
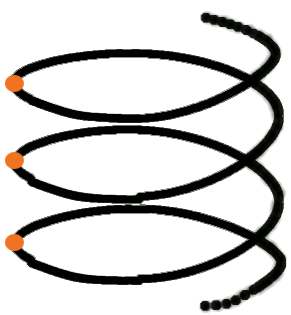
Usually the spiral curriculum was used for mathematical subjects and content areas. But it also possible to extend the spiral curriculum for typical mathematical activities and processes to enable a step-by-step acquirement of competence. Accounting this we generated a four level model to develop the competence “Reasoning and proof” from grade 5 to grade 12.
Four level model for arguing
The competence based four levels
Based on the forgoing our model includes 4 levels. All levels can occur in a specific field of arguing. And all levels can be visited in one particular grade or even across grades.[br][br][size=150][b]Level 1 – Disposition[/b][br]At this level students should have the disposition to engage in mathematical tasks that demand simple reasoning.[br][br][b]Level 2 – Comprehension[/b][br]At this level students should have the ability to understand, comprehend and explain prescribed reasons. An important aspect in this context is to identify the frame of reference. [br][br][b]Level 3 – Communication[/b][br]At this level students should have the ability to explain and argue completed mathematical proofs in communication situations.[br][br][b]Level 4 – Autonomy[/b][br]At this level students should autonomously find a reason for a (mathematical) statement / conjecture and / or an argument for this, including the choice of the frame of reference.[/size]
The competence based four level model
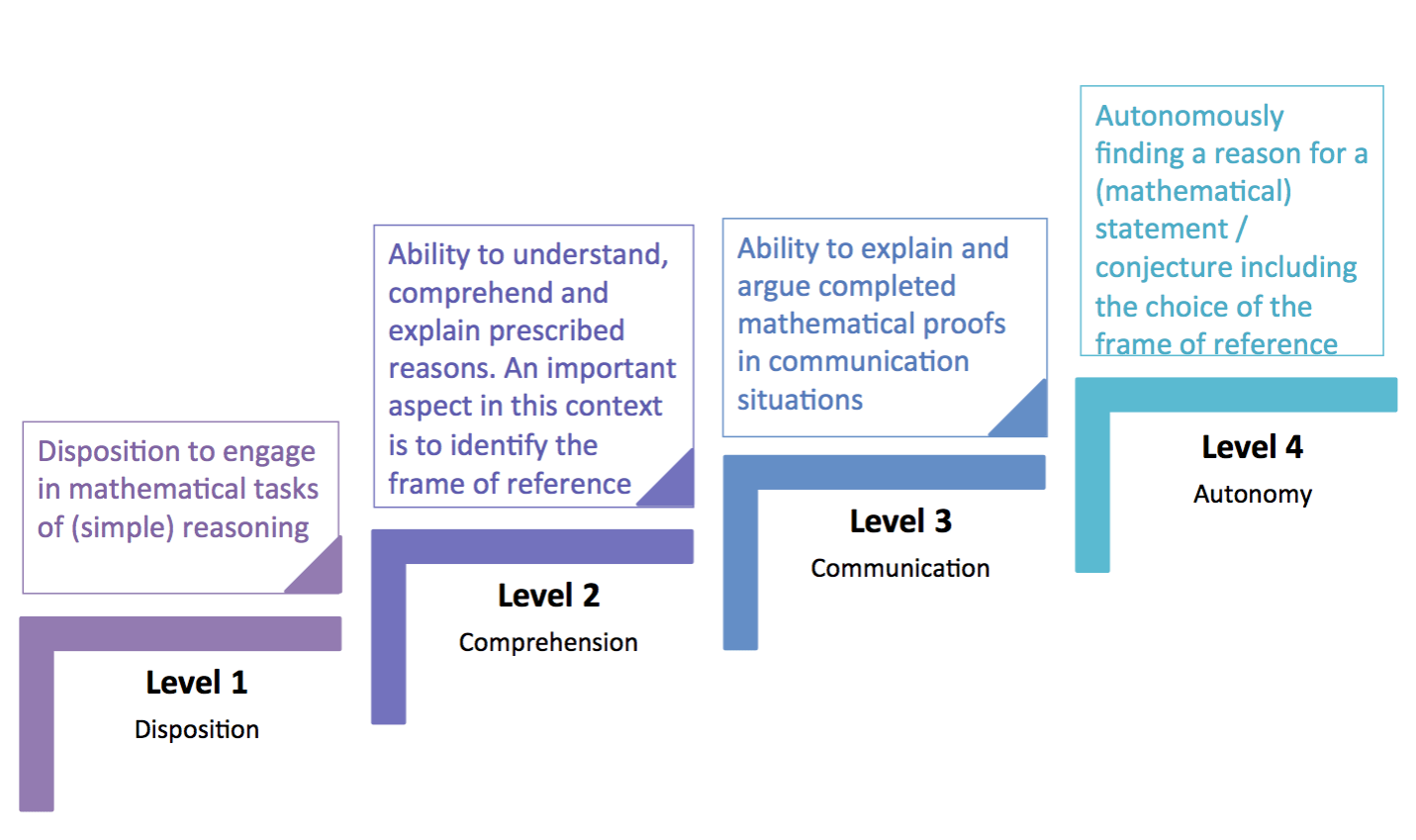
Süss-Stepancik & Götz 2015
[i]Four steps on the way to create argumentation competence supported by technology[/i]. Proceedings of CERME9
Surface Area - Trapezoid
Illustration of the four level model for arguing, reasoning and proof around surface areas.
Surface Area - Trapezoid
In Austria at grade 7 students deal with the surface areas of rectangles and triangles. The math curriculum at this grade demands that students should argue formulas for surface areas. This is a very broad field for arguing, reasoning and proof with various possibilities to use a paper and pencil approach as well as technology.[br][br]Let me now focus on the trapezoid and the derivation of the formula for the surface area.[br]I assume that the students already know the properties of the trapeze and the formula of the parallelogram before the start to deal with the area of the trapeze.[br][br]With an applet like the following students can easily and autonomously find the formula for the surface area of the trapeze. They "only" have to write down what they see and will find the formula autonomously. So with this applet student’s work at level 4.[br]If the students are asked to communicate and explain the formula of the surface of a trapeze they can also use the applet. And so they work at level 3.[br][br]
As you can imagine there are a lot of analogues applets for each rectangle and the derivation of area formulas. The main point is, that the applet should help to find the formula autonomously and it should support students by explaining the derivation.
Summary
[table] [tr] [td]1.) [/td] [td]Reasoning and proof requires continuing development.[/td][/tr] [tr] [td]2.) [/td] [td]Therefore we extend the spiral curriculum to mathematical activities.[/td][/tr] [tr] [td]3.) [/td] [td]With the competence based four level model (Disposition, Comprehension, Communication, Autonomy) for arguing the complexity of tasks that demand reasoning and proof can be identified.[/td][/tr] [tr] [td]4.) [/td] [td]GeoGebra-Applets [br]support the continuing development of arguing, because they can visualize the arguments of a proof and [br]refer to one or more different levels of the previous four level model.[/td][/tr][/table]