Fundamentals of Mathematics
This is a GeoGebraBook whose purpose is to be an aid for some subjects that I review with my students of the first Mathematics course at [i]PrepaTec[/i]. It contains activities and other resources aiming to improve the learning and teaching experience. For the picture: Walliman, D. (2018). Math Notation Cheat Sheet. flickr.com. https://www.flickr.com/photos/95869671@N08/40544016221/in/photostream/lightbox/.
Table of Contents
- Real numbers and Sets
- Real Number Classification - Introduction
- Rational and Irrational Number Classification
- Truncating and Rounding numbers
- Rounding Numbers (Quiz)
- Absolute value
- The Union and the Intersection of finite sets: Formative assessment
- Prime numbers
- Rational Numbers on a Numberline
- Rational Mastermind
- (Basics on) Arithmetic operations
- Prime factorization
- Greatest Common Factor and Least Common Multiple
- Simplifying fractions: Formative assessment
- Comparing Fractions
- Comparing fractions with lines and circles
- Operations between fractions
- Operations between fractions: formative assessment
- Order of operations and exponents
- Power rules
- Arithmetic deck
- Building Number Sentences: Open Middle Theme (5)
- Building Number Sentences: Open Middle Theme (6)
- Scientific notation, Ratios, Proportions and Percentages
- Ratios
- First steps into Proportions: Comparing ratios
- Creating Equal Ratios: Open Middle Theme
- Express in Scientific Notation
- Algebraic language and Addition of algebraic expressions
- Law of exponents
- Radicals
- Square root of a real number
- Radical simplification
- Perimeter and area
- Multiplication of algebraic expressions and Special products
- Factoring
- Factoring
- Algebraic fractions
Real Number Classification - Introduction
Review what you know about whole numbers, integers, rational numbers and irrational numbers that form the real number system by watching the video (8 min) below.
Rational and Irrational Numbers Exploration
[size=150]If you need to explore and visualize the rational numbers and irrational numbers and check whether they are terminating, non terminating and recurring or non recurring, use the interactive resource at [url=https://www.geogebra.org/m/hudgdmqu]https://www.geogebra.org/m/hudgdmqu[/url] .[/size]
Try this exercise to classify numbers in the second step
Real Number Systems (Descriptions/definition of terms) by AB Cron
Other Links to related resources on Rational and Irrational Numbers
[br]Ordering Irrational Numbers on the Number Line[br][url=https://www.geogebra.org/m/kezjxyec]https://www.geogebra.org/m/kezjxyec[/url][br][br]Ordering Rational and Irrational Numbers (Number Sense)[br][url=https://www.geogebra.org/m/hrrjgbp7]https://www.geogebra.org/m/hrrjgbp7[br][/url][br][br]Real Mastermind (Practice ordering numbers including irrational numbers, decimals, fractions, percentages[br][url=https://www.geogebra.org/m/mhvb33ea]https://www.geogebra.org/m/mhvb33ea[/url]
Prime factorization
Fundamental Theorem of Arithmetic
Every counting number greater than 1, can be represented in exactly one way apart from rearrangement as a product of one or more primes (Hardy and Wright 1979, pp. 2-3).
References
Amsavalli. (2020, October 24). [i]Prime factorization[/i]. GeoGebra. https://www.geogebra.org/m/rwrmctxp. [br][br]Hardy, G. H. and Wright, E. M. "Statement of the Fundamental Theorem of Arithmetic," "Proof of the Fundamental Theorem of Arithmetic," and "Another Proof of the Fundamental Theorem of Arithmetic." §1.3, 2.10 and 2.11 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 3 and 21, 1979.[br][br]Paudyal, C. P. (2020, October 24). [i]Prime factorization[/i]. GeoGebra. https://www.geogebra.org/m/eq2xdk6t. [br][br][br]
Power rules
Laws
[size=100]Let [math]x,y[/math] and [math]z[/math] be any three real numbers, and [math]n[/math] and [math]m[/math] be any two real numbers. Then the following statements hold true:[br][list][*][math]x^n \; x^m = x^{n + m}[/math].[/*][*][math]\left(x^n\right)^m=x^{nm}[/math].[/*][*][math]\left(x\; y\right)^n = x^n y^n[/math].[/*][*][math]x^0=1[/math]; provided that [math]x\ne0[/math].[/*][*][math]x^{-n}=\frac{1}{x^n}[/math]; provided that [math]x\ne0[/math].[/*][*][math]\frac{x^n}{x^m}=x^{n-m}[/math]; provided that [math]x\ne0[/math].[/*][*][math]\left(\frac{x}{y}\right)^n=\frac{x^n}{y^m}[/math]; provided that [math]y\ne0[/math].[/*][/list][/size]
Formative assessment
The purpose of the following applet is to practice simplifying algebraic expressions using the [b]Exponent Laws.[br][/b]Type in your answers in the boxes below (use ^ to write the power; for instance x^3 means [math]x^3[/math]).
References
Weisstein, Eric W. "Exponent Laws." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/ExponentLaws.html
Ratios
A [b]ratio [/b]is a quotient of two quantities. They are useful to [b]compare [/b]how two magnitudes relate (it quantifies such relation).[br]The [b]ratio [/b]between two numbers a and b is often written as:[list][*] [math]a[/math] to [math]b[/math], or[/*][*] [math]a:b[/math], or[/*][*] [math]\frac{a}{b}[/math].[/*][/list]
Square root of a real number
Square root
[b][br]Definition:[/b] A square root of a number [math]x[/math] is a number [math]r[/math] such that [math]r^2=x[/math].[br][b][br]Notation:[/b] If [math]r[/math] is a square root of a number [math]x[/math], then we will write [math]r=\sqrt{x}[/math].[br]
Construction of the square root of a real number using straight ruler and compass
On a straight line we mark off [i][math]OA=a[/math] [/i]and [math]AB=1[/math]. We draw a circle with the segment [i][math]OB[/math][/i] as its diameter and construct the perpendicular to [i][math]OB[/math][/i] through [i][math]A[/math][/i], which meets the circle in [i][math]C[/math][/i]. The triangle [i][math]OBC[/math][/i] has a right angle at [i][math]C[/math][/i], by the theorem of elementary geometry which states that an angle inscribed in a semicircle is a right angle. Hence, [math]\angle OCA[/math] = [math]\angle ABC[/math], the right triangles [i][math]OAC[/math][/i] and [i][math]CAB[/math][/i] are similar, and we have for [i][math]x=AC[/math][/i]:[br][br][center][math]\frac{a}{x}=\frac{x}{1}[/math][br][math]x^2=a[/math][br][math]x=\sqrt{a}[/math].[/center]
References
Courant, R., Courant, R., Robbins, H., Stewart, I., Courant, R., Courant, R., Robbins, H., & Robbins, H. (1996).[br][i]What is mathematics?: an elementary approach to ideas and methods[/i]. Oxford University Press.[br][br][i]Square Root[/i]. from Wolfram MathWorld. (n.d.). https://mathworld.wolfram.com/SquareRoot.html.[br]
Applet
Write the number whose square root you want to find. Next use the slider to animate the construction.
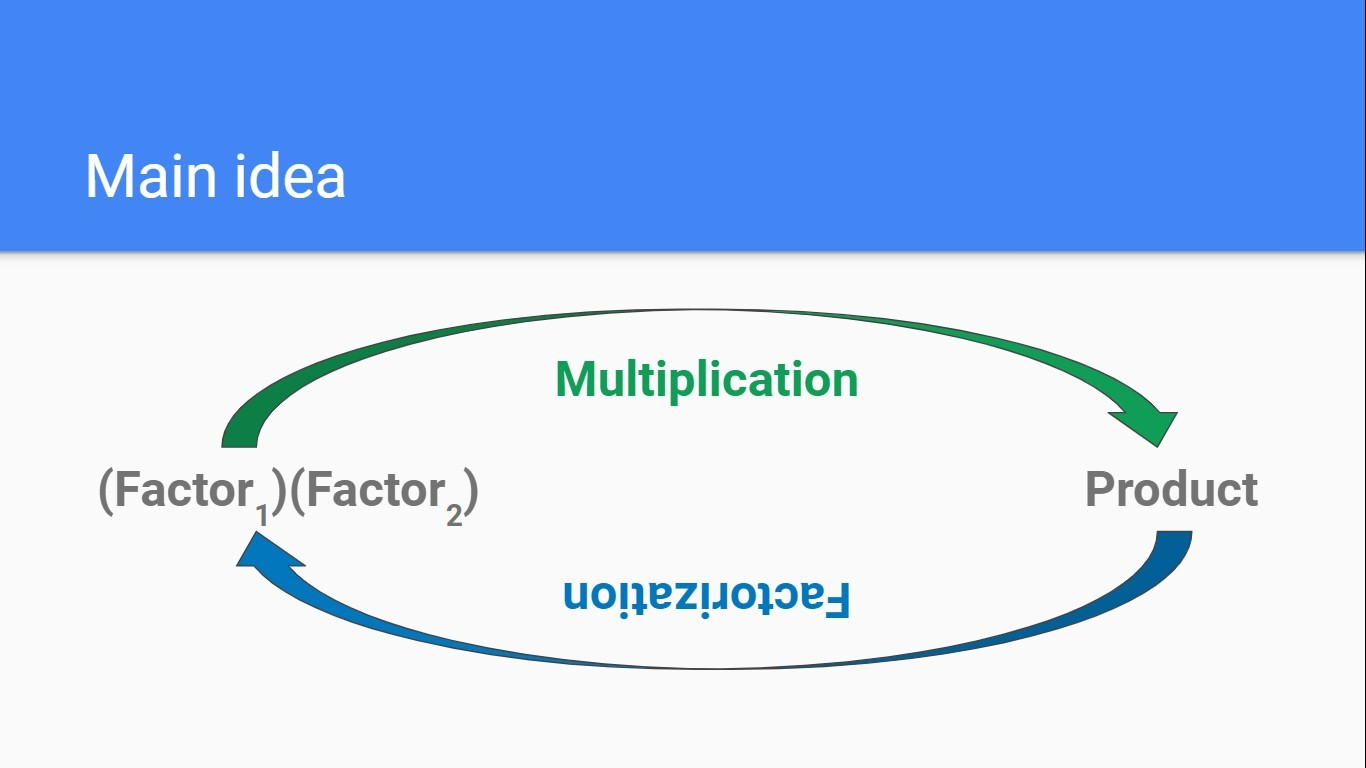
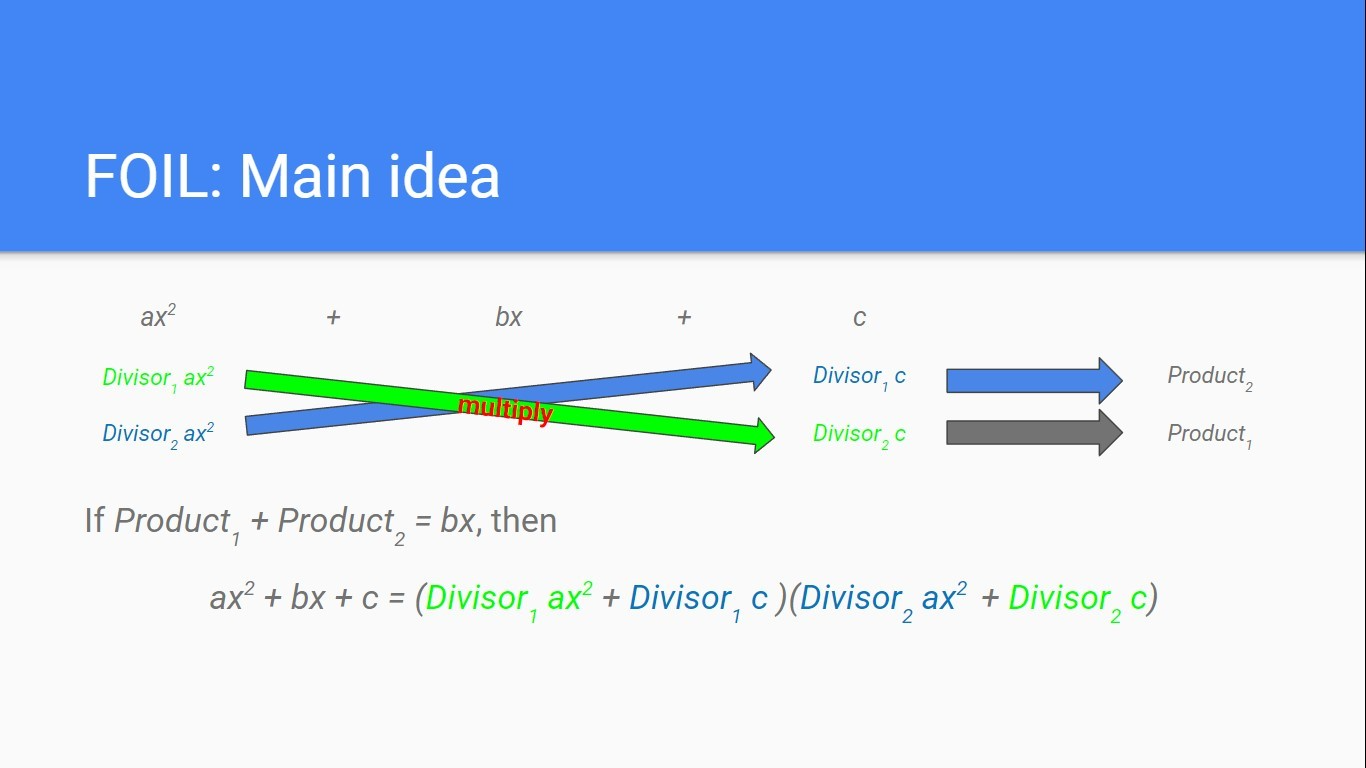
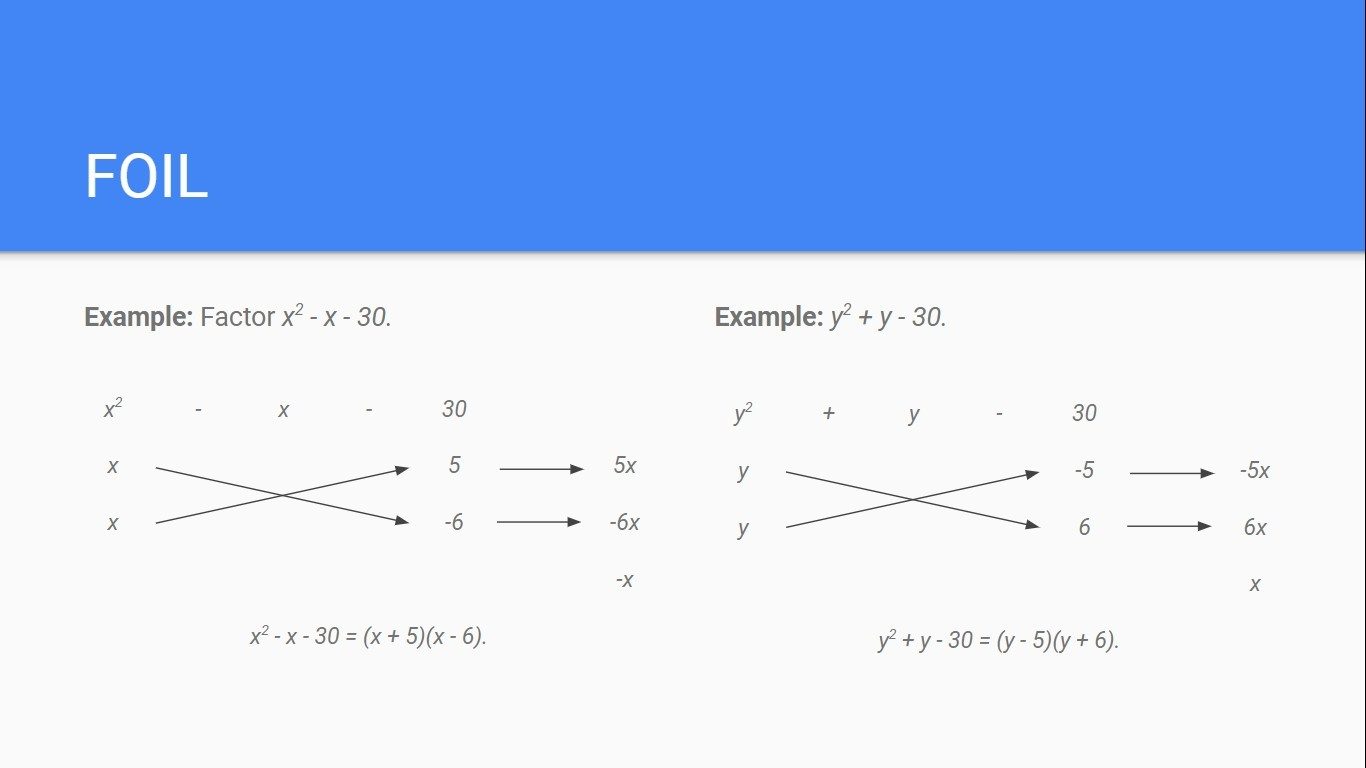
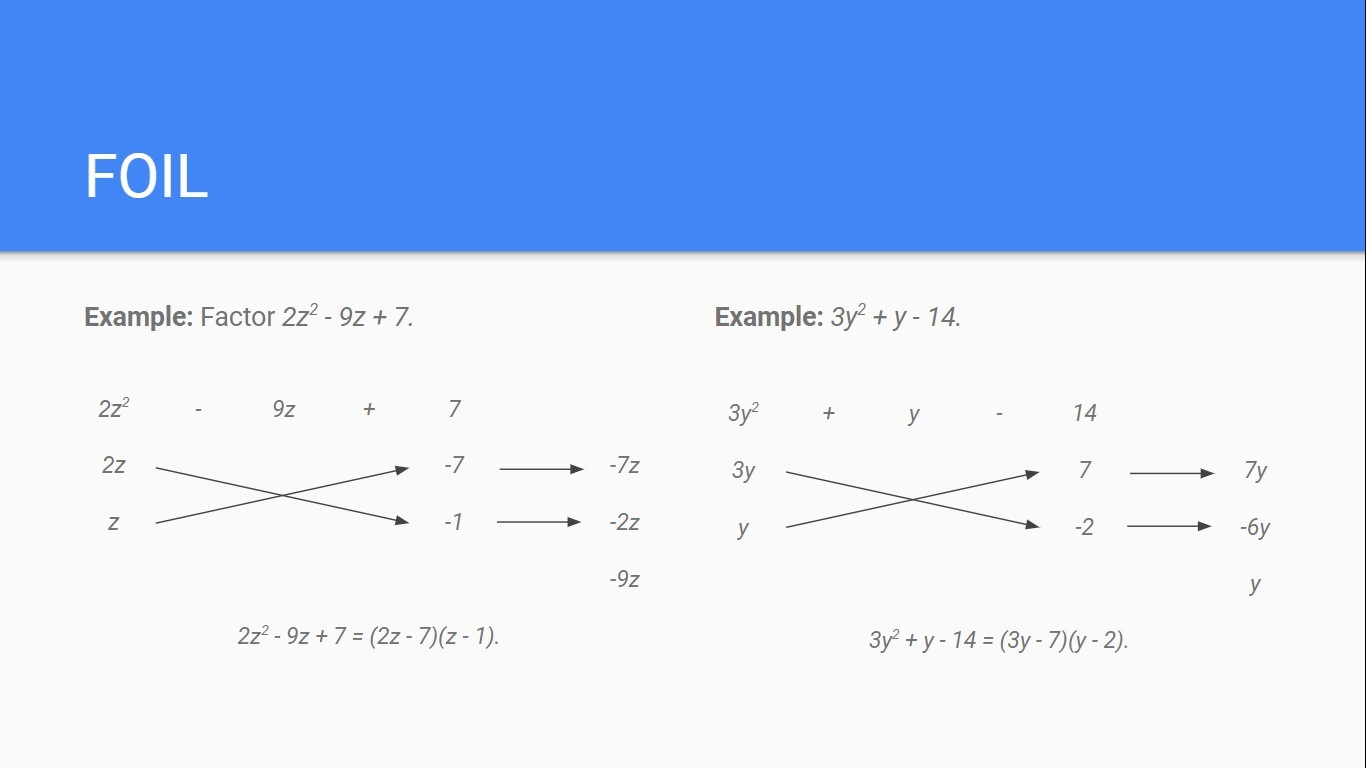
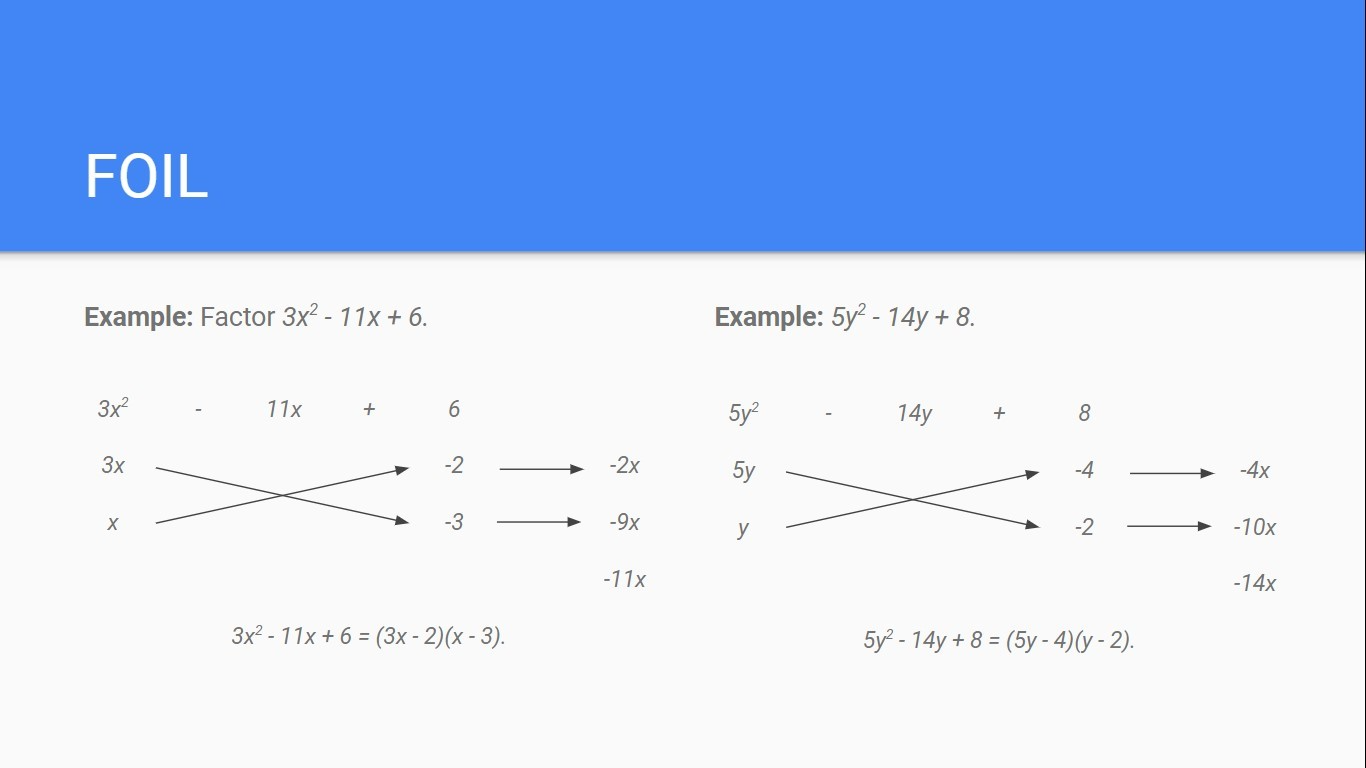
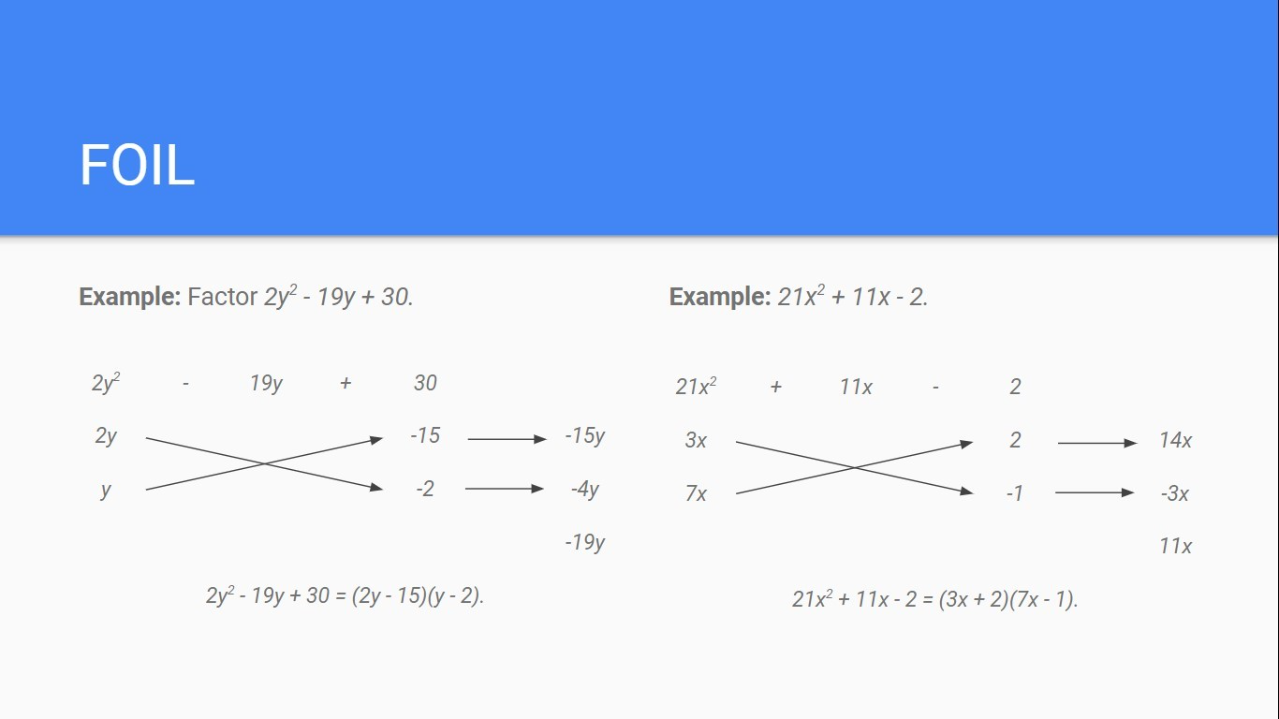
Factoring
