Effective ways to Learn and Teach Mathematics
Effective ways to learn and teach mathematics using the GeoGebra Software.
Table of Contents
- Introduction
- Basic Interfaces and Tools
- Quadratic Equations
- Vieta's Formula for Quadratic Equations
- Matrices
- Algebraic Operations on Matrices
- Algebraic Operations on Matrices - Order 3
- Vectors
- Addition of two Vectors in Three Dimensional
- Functions
- Functions
- Derivative of a Function
- Derivative of a Function
- Continuous at a point
- Complex Numbers
- Algebraic operations on Complex Numbers
- n th roots of unity - 21 december 2021
- Parts of a Circle
- parts of circle
- The perpendicular bisector of a chord
- Angle subtended by an arc or chord
Basic Interfaces and Tools
Introduction
[center][b][/b][/center][justify][b]GeoGebra is an open-source Dynamic Mathematics[br]Software for teaching and learning mathematics from middle school through[br]college level.[br][br]With an easy user interface, it is not only a popular Dynamic Geometry Software but also[br]provides basic features of Computer Algebra Systems to bridge some gaps between[br]geometry, algebra, and calculus.[/b][/justify]
Interfaces
[center][b][size=200]GeoGebra has [/size][/b][b][size=200]three basic interfaces[/size][/b][/center][center][b]1. Algebra View[br][br]2. Spreadsheet View[br][br]3. Graphics View[br] and[br][/b][b][size=200]Two advanced interfaces[/size][/b][br][br][b]4. 3D Graphics View[br][br]5. CAS ( Computer Algebra System)[/b][/center]
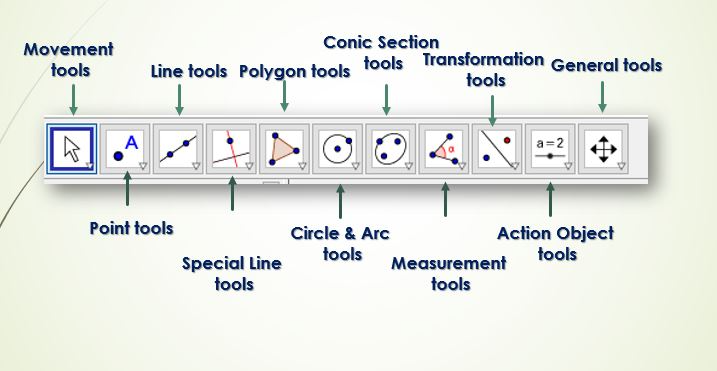
Basic Tools
Vieta's Formula for Quadratic Equations
Algebraic Operations on Matrices
[center][color=#0000ff][b][u]Algebraic Operations on Matrices[/u][/b][/color][/center][br][b][color=#0000ff]Basic operations on Matrices are[/color][br][/b][justify][br]1. Multiplication of a Matrix by a scalar, [br]2. Addition / Subtraction of two Matrices, and [br]3. Multiplication of two Matrices[/justify][justify][/justify][br][justify][color=#ff0000]NOTE:[/color] There is no concept of dividing a matrix by another matrix and thus, the operation [math]\frac{A}{B}[/math], where [math]A[/math] and [math]B[/math] are matrices, is not defined.[/justify]
Addition of two Vectors in Three Dimensional
Functions
we construct an applet to establish geometrically the correspondence of a number and its image under a function.
Derivative of a Function
Derivative of a function at a point
Derivative of a function at a point is the slope of the tangent to the corresponding curve at that point.
Algebraic operations on Complex Numbers
sum and difference of two complex numbers.[br]try to find the product of two complex numbers using the input command[br]z_1*z_2