Trigonometry
[i]Trigonometry for Dummies[/i] by Kenneth Choi
Table of Contents
- What is Trigonometry?
- What is Trigonometry?
- A Review of Geometry
- Triangles: Basic Geometry
- Introduction to Right Angle Trigonometry
- The Three Main Trigonometric Functions
- "Soh Cah Toa"
What is Trigonometry?
What is Trigonometry?
Trigonometry is the branch of mathematics that deals with triangles. In this book, you will learn many useful formulas and how Trigonometry is applied in the real world.
Triangles: Basic Geometry
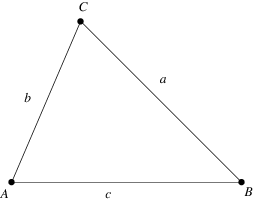
This is an example of a [b]triangle[/b]. The sum of the angle measures in a triangle is always [math]180^\circ[/math].
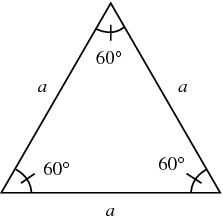
This is an [b]equilateral triangle[/b]. Each angle in an equilateral triangle is [math]60^\circ[/math]. The sides are all equal in length. Each side is represented by [i]a[/i] in this diagram.
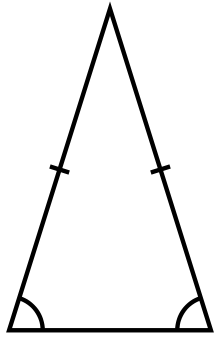
This is an [b]isosceles triangle[/b]. Two of the angles in an isosceles triangle are equal, and the other one is different. The two sides opposite these two equal angles are also equal to each other.
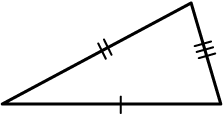
This is a [b]scalene triangle[/b]. All of the angles are different in a scalene triangle. All of the sides are also unequal.
The Three Main Trigonometric Functions
The three main trigonometric functions are sine, cosine, and tangent. Sine is abbreviated as [math]sin[/math], cosine is abbreviated as [math]cos[/math], and tangent is abbreviated as [math]tan[/math]. Don't worry if they seem intimidating at first. You'll get the hang of them.
You might have already seen these buttons on your calculator. Trigonometry is used for many other branches of math. That's why it is important for you to learn Trigonometry before venturing the harder math levels, such as Precalculus and Calculus.
Sine, cosine, and tangent all have to deal with angle and side proportions. For example, if you are talking about angle [i]a[/i] above, you can use the expressions [math]sin\left(a\right)[/math], [math]cos\left(a\right)[/math], and [math]tan\left(a\right)[/math] to relate angle [i]a[/i] with the sides of the triangle.