[size=85] The Heatmap, created by scanning outside parameter [b][color=#980000]c∈[c01,c02][/color][/b], draws black and white curves.[/size]
Double Orthogonal System of Curves
A double orthogonal system of curves, otherwise known as orthogonal trajectories, is made up of two families of curves where each curve in one family intersects each curve in the other family at right angles.
Table of Contents
- Double Orthogonal System of Curves gradient fields for the multifocal scalar function φ(r)=Σqₖ*|rₖ –r|ᵐ
- Visualisation of the gradient fields of a multifocal (k = 1..n) curve with n foci for a generalised potential function of the form φ(r)=Σqₖ*|rₖ –r|ᵐ, where m∈ℝ
- Description of applet tools: The generalized potential function has the form φ(r)=Σqₖ*|rₖ –r|ᵐ, where m is a real number
- + +. Visualization of scalar and vector fields of system of two positive point charges. The generalized potential function has the form φ(r)=Σqₖ*|rₖ –r|ᵐ, where m is a real number
- + -. Visualization of scalar and vector fields of system of two positive point charges. The generalized potential function has the form φ(r)=Σqₖ*|rₖ –r|ᵐ, where m is a real number
- Images for m=-1. The generalized potential function has the form φ(r)=Σqₖ*|rₖ –r|ᵐ, where m is a real number
- Images for m=1. The generalized potential function has the form φ(r)=Σqₖ*|rₖ –r|ᵐ, where m is a real number
- Images for m=0.4. The generalized potential function has the form φ(r)=Σqₖ*|rₖ –r|ᵐ, where m is a real number
- Images of 8 examples (m = -1) of visualizations of scalar and vector fields using Equipotential, Vector Field and Iso-Magnitude Lines. The potential function is φ(r) = Σqₖ*|rₖ –r|ᵐ
- Images of 6 examples (m = 0.4) of visualizations of scalar and vector fields using Equipotential, Vector Field and Iso-Magnitude Lines. The potential function is φ(r) = Σqₖ*|rₖ –r|ᵐ
- Images of 11 examples (m =1) of visualizations of scalar and vector fields using Equipotential, Vector Field and Iso-Magnitude Lines. The potential function is φ(r) = Σqₖ*|rₖ –r|ᵐ
- Double Orthogonal System of Curves gradient fields for the multifocal scalar function φ(r)= Π|rₖ –r|
- Visualisation of the gradient fields of a multifocal Cassinian curves with n foci, for a potential function of the form: φ(r) = Π|rₖ –r|, where k = 1.. n
- Images 5 examples of visualization of scalar and vector fields for multifocal Cassini curves with n foci whose potential function is φ(r) = Π|rₖ –r|, where k = 1.. n
Visualisation of the gradient fields of a multifocal (k = 1..n) curve with n foci for a generalised potential function of the form φ(r)=Σqₖ*|rₖ –r|ᵐ, where m∈ℝ
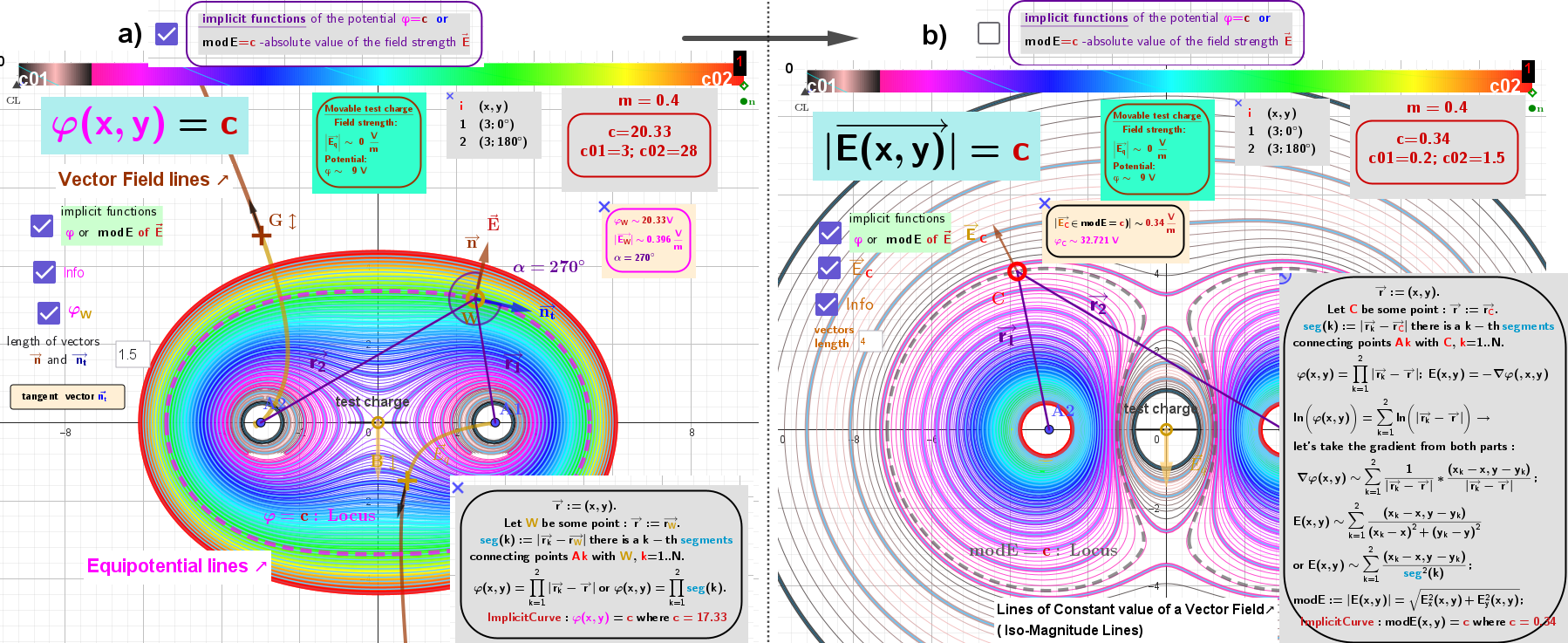
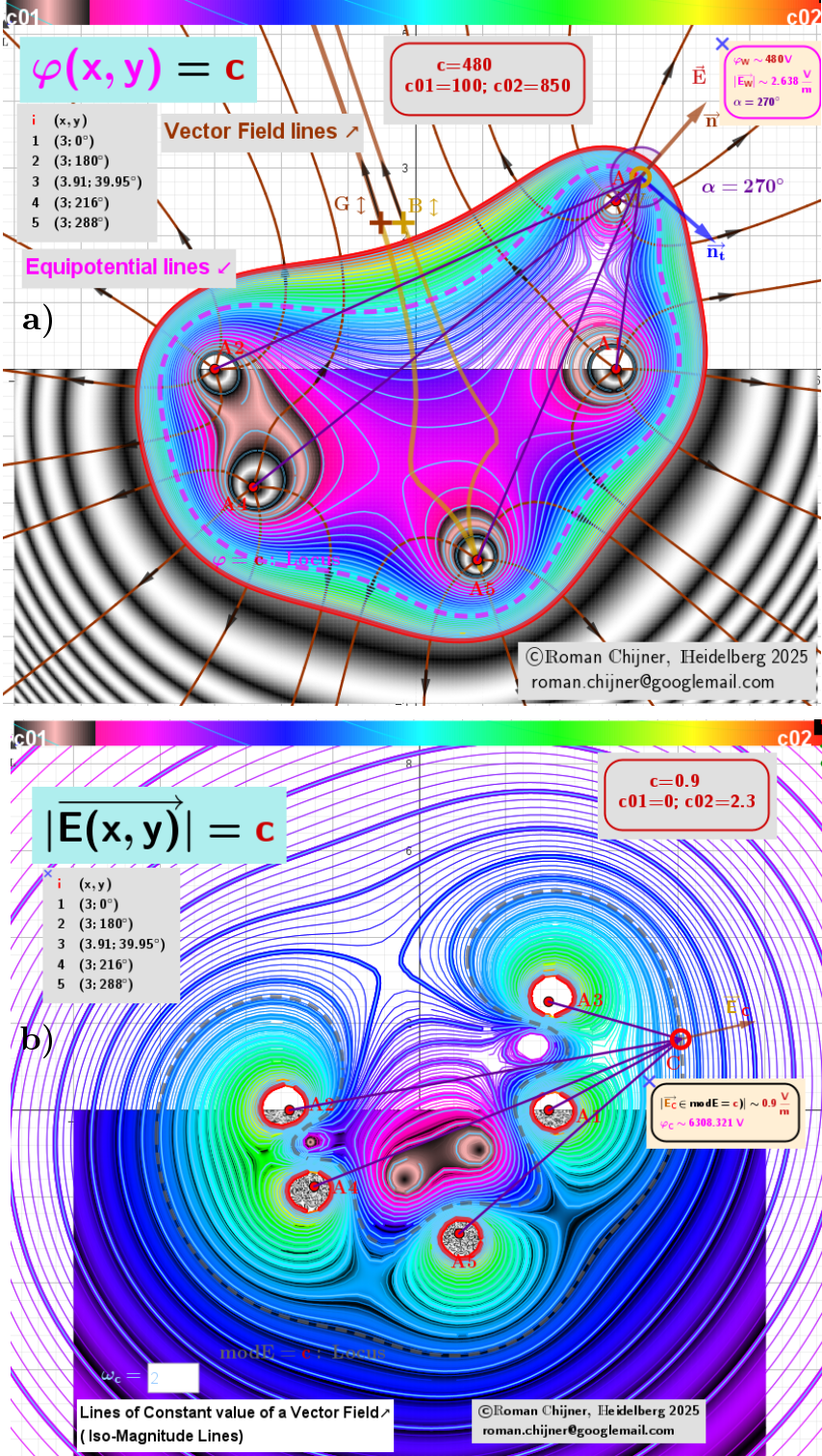
[size=85][i] A [/i][url=https://en.wikipedia.org/wiki/Generalized_conic]multifocal oval[/url][i] is a curve defined as the [/i][b]locus[/b][i] of a point A([b]r[/b]) that moves in such a way that the [/i][b][color=#0000ff]sum of the distances [/color][/b][color=#ff00ff][b]φ[/b][/color][i]([b]r[/b]) [b][color=#0000ff]to[/color][/b] [/i][b]n[/b][i] [b][color=#0000ff]points[/color][/b] remains constant. It is also known as a [/i][url=https://mathcurve.com/courbes2d.gb/multiellipse/multiellipse.shtml][color=#ff7700]Multifocal Ellipse[/color][/url][i] ([/i][url=https://en.wikipedia.org/wiki/N-ellipse][color=#980000][i]n[/i]-ellipse[/color][/url][i]) with [/i][b]n [/b][b][color=#ff0000]foci[/color][/b][i] (or [b]n[/b] poles).[br] The potential function [b][color=#ff00ff]φ[/color][/b]([b]r[/b]) is generalized by this applet to generate the corresponding multifocal curves.[br] [/i][size=85][i][i][i][i][i][i][i][i][i][b][i][i][i][b][i][b][i][b][b][i][color=#767676]The [/color][color=#0000ff]sum[/color][color=#0000ff] o[/color][color=#0000ff]f t[/color][size=85][color=#0000ff]he m-th powers of the distances [/color][color=#0000ff]to [/color][color=#333333]n[/color][color=#0000ff] points[/color][color=#333333] is given here by [/color][/size][/i][/b][/b][/i][/b][/i][/b][/i][/i][/i][/b][/i][/i][/i][/i][/i][/i][/i][/i][/i][color=#0000ff][color=#0000ff][color=#0000ff][size=85][color=#ff00ff][b]φ[/b][/color][color=#333333][b](r)=[/b][i][i][i][i][i][i][i][i][b]Σqₖ*|rₖ–r|ᵐ[/b][/i][/i][/i][/i][/i][/i][/i][/i], where k=1..[b]n[/b] and [b]m∈ℝ[/b]. [b]qₖ[/b] - weight factors, which here, by analogy with electromagnetism, we will call "charges". [/color][/size][/color][/color][/color][/size][br][i][br] ●The purpose of the applet is to visualise [/i][url=https://mathcurve.com/courbes2d.gb/orthogonale/orthogonale.shtml]double orthogonal systems[/url][i] for [/i][color=#9900ff]scalar[/color][i] functions of the above type. In particular: [/i][i]for [/i][b]m[/b][i] = -1, this is the well-known result in electromagnetism that electric [/i][color=#980000]field lines[/color][i] and [/i][color=#ff00ff]equipotential lines[/color][i] form a double orthogonal system. For [b]m[/b]=1 -[url=https://en.wikipedia.org/wiki/N-ellipse][i]n[/i]-ellipse[/url] , [b]m[/b]=2 - [url=https://www.geogebra.org/material/show/id/arrctwvn]case[/url]. [br]●The applet constructs [/i][b]loci[/b][i]. For a [color=#9900ff]given [url=https://www.google.com/search?q=what+Scalar+field&sca_esv=b3f6a4e4ace9f962&rlz=1C1VDKB_deDE963DE963&sxsrf=AE3TifNaeH1mlgh2NkZ_lPDl2gyWT2xiLg%3A1752848303285&ei=r1d6aLOYEYmrxc8PkrqOoAs&ved=0ahUKEwjzq9njzMaOAxWJVfEDHRKdA7QQ4dUDCBA&oq=what+Scalar+field&gs_lp=Egxnd3Mtd2l6LXNlcnAiEXdoYXQgU2NhbGFyIGZpZWxkMgYQABgHGB4yBhAAGAcYHjIGEAAYBxgeMgYQABgHGB4yBhAAGAcYHjIGEAAYBxgeMgYQABgHGB4yBhAAGAcYHjIGEAAYBxgeMgYQABgHGB5I9DRQqRNYyydwAXgBkAEAmAFxoAGDBKoBAzIuM7gBDMgBAPgBAZgCBqAClQTCAgoQABiwAxjWBBhHwgINEAAYgAQYsAMYQxiKBcICBxAAGIAEGA2YAwCIBgGQBgqSBwMzLjOgB-ousgcDMi4zuAeQBMIHBTAuNS4xyAcP&sclient=gws-wiz-serp]scalar field[/url] [/color][/i][color=#ff00ff][b]φ[/b][/color][i](r), it creates [br][/i][color=#ff00ff]-equipotential lines[/color][i], and for the corresponding gradient fields [/i][b]E[/b][i](r), it creates [br]-iso-magnitude lines, which are lines of constant field magnitude ([/i][color=#1e84cc]but not their direction![/color][i]), denoted by [/i][b][color=#333333][url=https://www.google.com/search?sca_esv=9df8d0d36b3fc424&rlz=1C1VDKB_deDE963DE963&sxsrf=AE3TifOinHFuIQvbGNLrnpGmgfmwCNS3IQ:1751026231589&q=what+is+Equi-lines+potential+%CF%86+and+modE&spell=1&sa=X&ved=2ahUKEwjMxZqEyZGOAxW_FBAIHQEZGxMQBSgAegQICxAB]modE[/url][/color]. [/b][i]The vector field [/i][b]E[/b][i](r) is obtained by taking the[/i][b][color=#980000] [url=https://en.wikipedia.org/wiki/Gradient]gradient[/url] [/color][/b][i]of the potential function [color=#ff00ff][b]φ[/b][/color](r)[/i][i].[br]● For a set of point "charges", these [/i][b]loci[/b][i] are always closed, and the "charges" are their [/i][b][color=#ff0000]foci[/color][/b][i]. In other words, these lines are multifocal curves[/i][i].[br]● [/i][color=#ff00ff]Equipotential lines[/color][i] are [/i][color=#333333][i]always perpendicular [/i][/color][i]to the [color=#980000]field lines[/color][/i][i] of the [/i][url=https://en.wikipedia.org/wiki/Conservative_vector_field]conservative[/url][i] vector field [/i][b]E[/b][i](r), which are calculated numerically in the applet.[br][/i][/size] [size=85]Description of Services of this applet you will find in [url=https://www.geogebra.org/m/adevardg ]1[/url], images of examples in [url=https://www.geogebra.org/m/vvqwdngb ]2[/url], [url=https://www.geogebra.org/m/htxqtc5v ]3[/url], [url=https://www.geogebra.org/m/qqbbe28g]4[/url], [url=https://www.geogebra.org/m/hzsb6a5p ]5[/url], [url=https://www.geogebra.org/m/yjtysjma ]6[/url], [url=https://www.geogebra.org/m/wd2bxbd6 ]7[/url], [url=https://www.geogebra.org/m/remwjr7t ]8[/url], [url=https://www.geogebra.org/m/ygtcty7y ]9[/url].[/size]
[b][color=#980000]Examples of five charges [/color][/b]
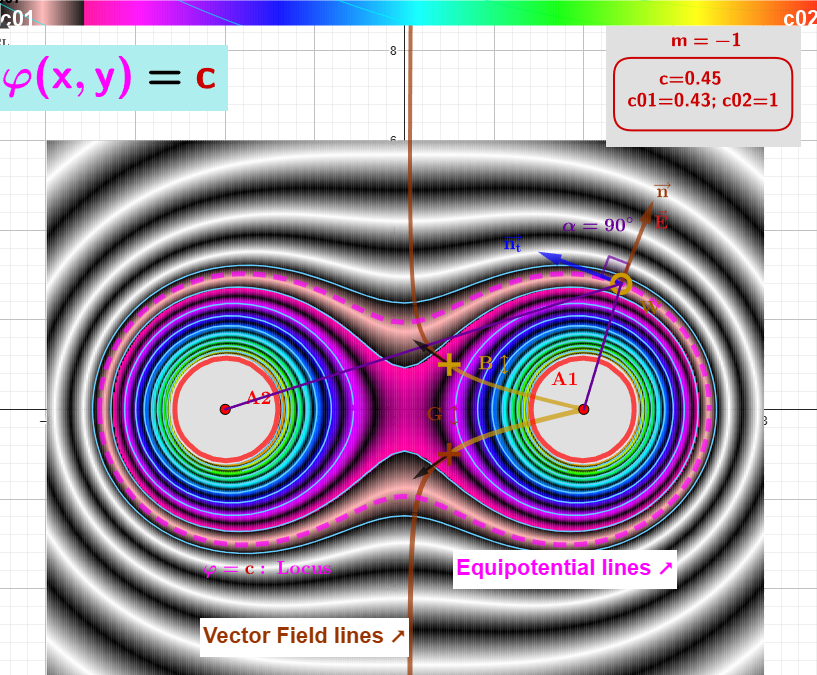
[size=85][b][color=#333333]Figure 1:[/color][/b][color=#333333]The [/color][i][b][color=#ff00ff]equipotential lines[/color][/b][/i][color=#333333] of a scalar field [/color][b][color=#ff00ff]φ [/color][/b][color=#333333]are always perpendicular to the [/color][i][color=#980000][b]lines of force[/b] [/color][color=#333333]of the corresponding gradient field [/color][/i][b]E[/b][color=#333333]. [/color][br][/size]
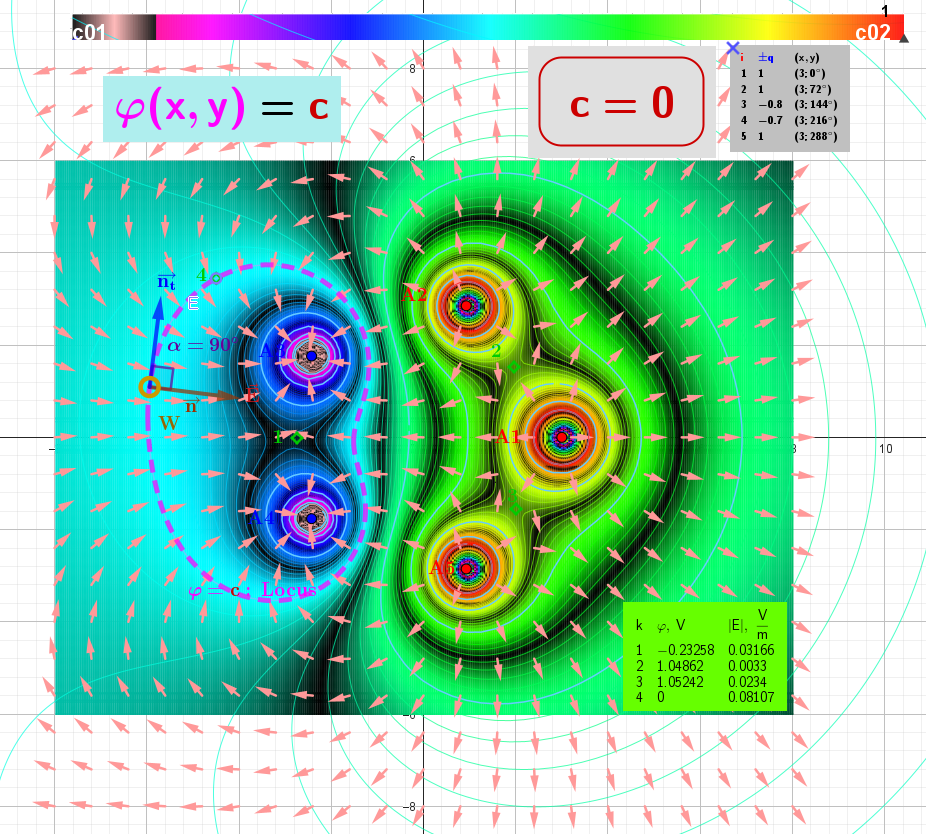
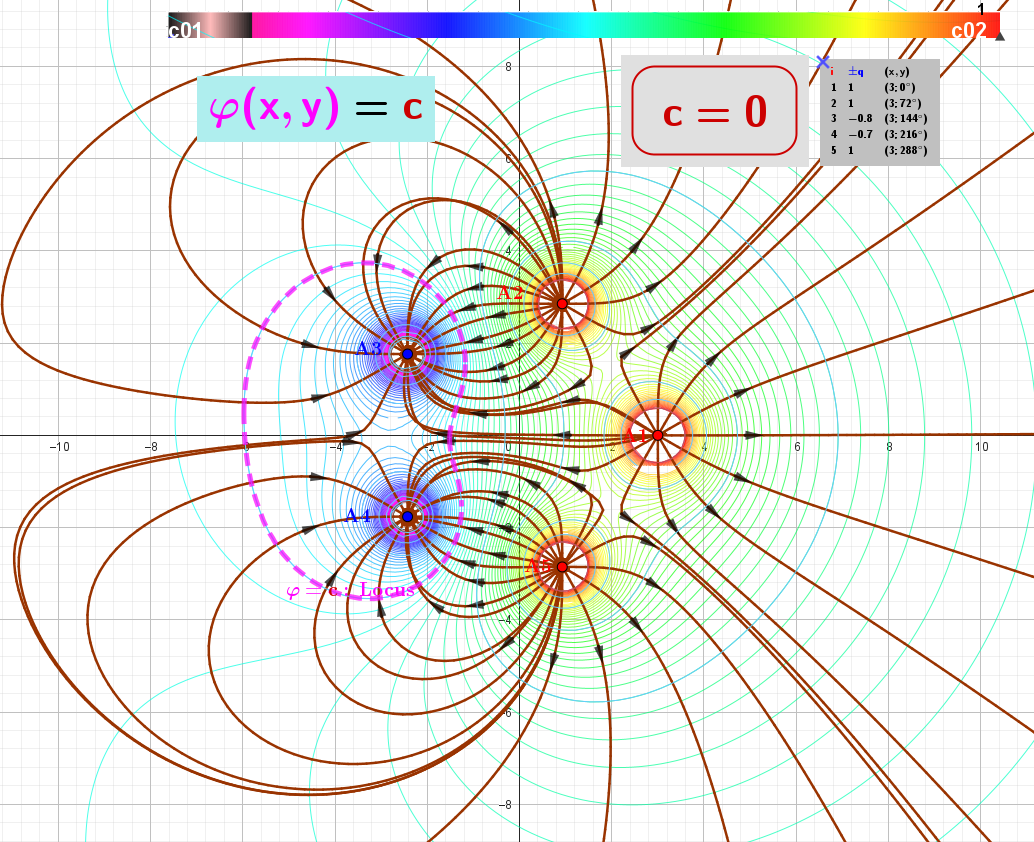
[size=85][b]Figure 2: [/b][color=#333333]The [/color][b]Heatmap [/b][color=#333333]showing the distribution of the scalar field [/color][b][color=#ff00ff]φ[/color][/b][color=#333333] around the charges, along with the directions of the corresponding gradient vector field [/color][b]E[/b][color=#333333], is depicted as [/color][b][color=#ea9999]arrows[/color][/b][color=#333333]. Here the [/color][b][color=#ff00ff]Equipotential lines[/color][/b][color=#333333] of the scalar field [/color][b][color=#ff00ff]φ[/color][/b][color=#333333] are closed curves whose [/color][b][color=#ff0000]foci[/color][/b][color=#333333] are located on the charges.[/color][/size]
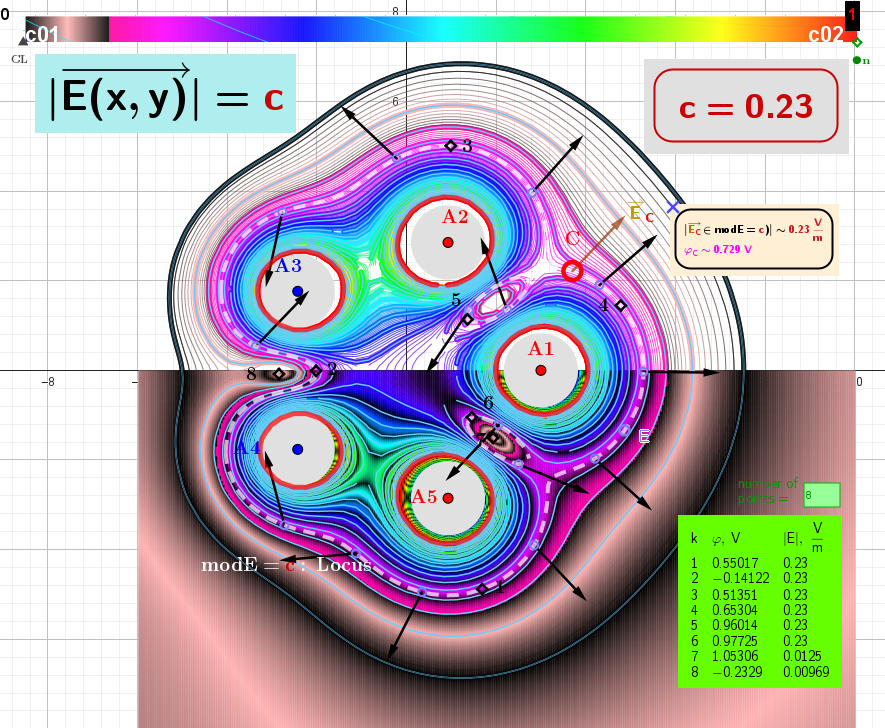
[size=85][b][color=#333333]Figure 3[/color][color=#980000]: [/color][/b]The [b]Heatmap[/b] and [b]Contour lines[/b] shows the distribution of the [i]constant value of the vector field strength modulus[/i] [b]E[/b] for five point charges (denoted [b]modE[/b]). In this case, the [i]lines representing the constant value of the vector field strength[/i] modulus [b]E[/b] (but not their directions!) always form closed curves, the [b]foci[/b] of which are[i] located at the charges[/i].[br][/size] [size=85]The table shows the values of the potential [b][color=#ff00ff]φ[/color][/b] and [b]modE[/b] at test points 1–6, which are located on the locus [b]modE[/b]=[color=#980000][b]c[/b][/color]. Test points 7 and 8 are at points where the field [b]E[/b] is almost zero.[/size]
Visualisation of the gradient fields of a multifocal Cassinian curves with n foci, for a potential function of the form: φ(r) = Π|rₖ –r|, where k = 1.. n
[size=85][i] The [i][url=https://www.mathcurve.com/courbes2d.gb/cassinienne/cassinienne.shtml]Cassinian curves[/url] with[/i] [i][b]n[/b][/i] [i]foci[/i] (or [i][b]n[/b] poles[/i]) are the loci of the points [b]A(r) [/b]on the plane for which the [b]geometric mean of the distances[/b] to [i][b]n[/b][/i] points is constant. When [i][b]n[/b][/i] = 2, we get the [url=https://www.mathcurve.com/courbes2d.gb/cassini/cassini.shtml]Cassini ovals[/url].[br]●The purpose of the applet is to visualise [/i][url=https://mathcurve.com/courbes2d.gb/orthogonale/orthogonale.shtml]double orthogonal systems[/url][i] for [/i][color=#9900ff]scalar[/color][i] functions of the form: [b][color=#ff00ff]φ[/color][/b]([b]r[/b]) = [b][size=100]Π[/size][/b]|[b]rₖ[/b] –[b]r[/b]|, where k = 1.. [b]n[/b].[br][/i][i]●The applet constructs [/i][b]loci[/b][i]. For a [color=#9900ff]given [url=https://www.google.com/search?q=what+Scalar+field&sca_esv=b3f6a4e4ace9f962&rlz=1C1VDKB_deDE963DE963&sxsrf=AE3TifNaeH1mlgh2NkZ_lPDl2gyWT2xiLg%3A1752848303285&ei=r1d6aLOYEYmrxc8PkrqOoAs&ved=0ahUKEwjzq9njzMaOAxWJVfEDHRKdA7QQ4dUDCBA&oq=what+Scalar+field&gs_lp=Egxnd3Mtd2l6LXNlcnAiEXdoYXQgU2NhbGFyIGZpZWxkMgYQABgHGB4yBhAAGAcYHjIGEAAYBxgeMgYQABgHGB4yBhAAGAcYHjIGEAAYBxgeMgYQABgHGB4yBhAAGAcYHjIGEAAYBxgeMgYQABgHGB5I9DRQqRNYyydwAXgBkAEAmAFxoAGDBKoBAzIuM7gBDMgBAPgBAZgCBqAClQTCAgoQABiwAxjWBBhHwgINEAAYgAQYsAMYQxiKBcICBxAAGIAEGA2YAwCIBgGQBgqSBwMzLjOgB-ousgcDMi4zuAeQBMIHBTAuNS4xyAcP&sclient=gws-wiz-serp]scalar field[/url] [/color][/i][color=#ff00ff][b]φ[/b][/color][i](r), it creates [br][/i][color=#ff00ff]-equipotential lines[/color][i], and for the corresponding gradient fields [/i][b]E[/b][i](r), it creates [br]-iso-magnitude lines, which are lines of constant field magnitude ([/i][color=#1e84cc]but not their direction![/color][i]), denoted by [/i][b][color=#333333][url=https://www.google.com/search?sca_esv=9df8d0d36b3fc424&rlz=1C1VDKB_deDE963DE963&sxsrf=AE3TifOinHFuIQvbGNLrnpGmgfmwCNS3IQ:1751026231589&q=what+is+Equi-lines+potential+%CF%86+and+modE&spell=1&sa=X&ved=2ahUKEwjMxZqEyZGOAxW_FBAIHQEZGxMQBSgAegQICxAB]modE[/url][/color]. [/b][i]The vector field [/i][b]E[/b][i](r) is obtained by taking the [/i][url=https://en.wikipedia.org/wiki/Gradient]gradient[/url] [color=#333333]([size=85]Figure 1: ) [/size][/color][i]of the potential function [color=#ff00ff][b]φ[/b][/color](r).[br]● For a set of point "charges" (q[sub]k[/sub][/i]=1)[i], these [/i][b]loci[/b][i] are always closed, and the "charges" are their [/i][b][color=#ff0000]foci[/color][/b][i]. In other words, these lines are multifocal curves[/i][i].[br]● [/i][color=#ff00ff]Equipotential lines[/color][i] are [/i][color=#333333][i]always perpendicular [/i][/color][i]to the [color=#980000]field lines[/color][/i][i] of the [/i][url=https://en.wikipedia.org/wiki/Conservative_vector_field]conservative[/url][i] vector field [/i][b]E[/b][i](r), which are calculated numerically in the applet.[/i][/size]
Figure 1: Finding a vector field from a scalar field of type φ(r) = Π|rₖ –r|, by calculating its gradient: E = - ∇φ
[size=85] There are two different ways of representing loci for the system of "charges":[br]a) equipotential lines, [b][color=#ff00ff]φ(x,y) [/color]=[color=#980000]c[/color],[/b] and[br]b) lines of constant magnitudes of the corresponding conservative vector field, [b]modE =[color=#980000] c[/color][/b].[/size]
[size=85][size=100][b][u]Applet[/u]. Description of Services for the applet can be found in [url=https://www.geogebra.org/m/adevardg]1[/url]. There are 5 examples. You can download any of them [b]by clicking on the corresponding button[/b]. You will find their images in [b][b][url=https://www.geogebra.org/m/fbey4rs7]2[/url][/b].[/b][/b][/size][/size]
Figure 2: Heat maps and contour lines of the five charges showing:
[size=85]a) The distribution of the scalar field [color=#ff00cc][b]φ [/b][/color]around the charges, as well as the directions of the corresponding gradient vector field [b]E[/b], where the equipotential lines ([b][color=#ff00ff]φ[/color]=[color=#980000]c[/color]) [/b]of the scalar field are closed curves whose [b][color=#ff0000]foci[/color][/b] are located on the charges and perpendicular to the field[br]lines.[br](b) Distribution of the constant value of the modulus of the vector field strength [b]E [/b]for five point charges (denoted [b]modE[/b]). In this case, the lines representing the [b][i][color=#980000]constant[/color][/i][/b] modulus of the vector field strength [b]E (modE=[color=#980000]c[/color]) [/b]always form closed curves whose [b][color=#ff0000]foci[/color][/b] are located on the charges (but not their directions!).[/size]