Geometrische Formen identifizieren
Hallo!
[b]Herzlich Willkommen[/b] in diesem interaktiven Buch! [br][br]Schön, dass du da bist![br][br]Du kennst aus deinem Alltag bereits viele interessante Figuren...[br][br]In diesem Buch lernst du, Formen zu unterscheiden und in "Familien" zusammenzufassen. Anschließend kannst du zu verschiedenen Formen kennen, was sich hinter dem "Flächeninhalt" verbirgt.
Wie funktioniert?
Bearbeite die Aktivitäten der Reihe nach und beantworte die Fragen. [br]Wenn es für dich sinnvoll ist, kannst du einzelne Aktivitäten auch überspringen...
1. Formen erkennen und zuordnen
Du siehst eine geometrische Form.[br][list=1][*]Wähle passend aus, um welche Form es sich handelt. [br][/*][*]Klicke anschließend auf "Neue Aufgabe".[br][/*][/list]
2. Alltagsgegenstände richtig zuordnen.
Im Alltag tauchen immer wieder geometrischen Formen auf.[br][list=1][*]Wähle für die Form, die du siehst, aus, wie sie zugeordnet werden kann.[/*][*]Klicke anschließend wieder auf "Neue Aufgabe".[/*][/list]
3. Formen drehen und zuordnen
Formen können auch gedreht und in ihrer Größe angepasst werden. [br][list=1][*]Wähle hier die passende Form aus und drehe sie, indem du den Punkt daran gedrückt hältst. [/*][*]Schiebe die Figur dann auf das Bild und prüfe, ob du richtig liegst.[/*][/list]
4. Verkehrsschilder?
Teste hier, welche geometrischen Formen du in den verschiedenen Verkehrsschilder wiederfindest...!
5. Passende Formen finden.
In den grauen Feldern siehst du ein Dreieck, ein Viereck und einen Kreis.[br]Ziehe alle bunten Formen in das jeweils passende graue Feld.[br]
Jetzt die gleiche Aufgabe mit Gegenständen oder Objekten aus der realen Welt :)
Überblick: Welche geometrischen Formen gibt es?
Im folgenden Video kannst du dir nochmal einen Überblick verschaffen, welche geometrischen Formen es gibt...
Geometrische Figuren
Erarbeitung: Flächeninhalt von Rechtecken
Aufgabe:
Das Rechteck als geometrische Figur ist dir bereits bekannt. Sieh dich im Klassenzimmer um und identifiziere, wo du überall rechteckige Formen siehst![br][br][color=#ff7700]HEFT: [/color]Zeichne ein beliebiges Rechteck in dein Heft und markiere die rechten Winkel !
Nächster Schritt:
Nun wollen wir einen Weg finden, um den Flächeninhalt eines Rechtecks zu bestimmen. [br]Dazu nehmen wir uns ein Quadrat mit einem Zentimeter Länge und einem Zentimeter Breite zu Hilfe. Dieses Einheitsquadrat entspricht genau einem Quadratzentimeter (1[math]cm^2[/math]). [br][br][u]Aufgabe:[/u] [br]Erzeuge hier unterschiedliche Rechtecke (durch Anpassung der Länge und Breite) und zähle dann, wie viele von den Einheitsquadraten ([math]cm^2[/math]) in das Rechteck reinpassen ![br][br][br][br]
[color=#ff7700]HEFT:[/color] Trage die Länge und Breite eines von dir erzeugten Rechtecks und die Anzahl der Quadrate, die in das Rechteck reinpassen, in eine Wertetabelle in dein Heft ein ! So sollte die Wertetabelle ausschauen !

Letzte Aufgabe:[br][br]Findest du eine Möglichkeit, um ohne zu zählen sofort den Flächeninhalt des Rechtecks zu bestimmen?[br]Versuche, eine allgemeine Formel zur Berechnung des Flächeninhalts eines Rechtecks herauszufinden!
[size=150][color=#ff7700]Prüffragen:[br][br][/color][/size]1. Welchen Flächeninhalt hat ein Rechteck mit Länge 2 cm und Breite 5 cm ?
2. Welchen Flächeninhalt hat ein Rechteck mit Länge 5 dm und Breite 20 cm ?
Herleitung: Flächeninhalt Parallelogramm
Herleitung: Flächeninhalt vom Parallelogramm
Du kennst jetzt bereist die Formel zur Berechnung des Flächeninhalt vom Rechteck! Nun wollen wir uns eine neue Figur ansehen.
Verschiebe den Punkt D nach links oder rechts.
Welche neue Figur entsteht durch die Verschiebung?
Auf der Suche nach der Flächeninhaltsformel
Verschiebe den Punkt am Schieberegler und beobachte was passiert.
Die Visualisierung zeigt, dass aus dem Parallelogramm ein Rechteck entsteht. [br]Welche zwei Längen brauchst du zur Berechnung des Flächeninhalts des oben entstandenen Rechtecks?
Diese zwei Längen brauchst du demnach auch, um den Flächeninhalt des Parallelogramms zu berechnen. [br]Hast du schon eine Idee, wie man den Flächeninhalt eines Parallelogramms berechnet?[br]Denke an den Zusammenhang mit dem Rechteck!
Herleitung: Flächeninhalt Dreieck
Herleitung: Flächeninhalt von Dreiecken
Du kennst jetzt bereits die Formeln zur Berechnung des Flächeninhalts von Rechtecken und Parallelogrammen. Nun wollen wir uns eine neue Figur ansehen: das Dreieck.
Auf der Suche nach einer Flächeninhaltsformel …
Du siehst hier ein Dreieck. Verwende den Schieberegler und schaue was passiert.
Bezug zum Rechteck
Wie du bereits weißt kann man den Flächeninhalt eines Parallelogramms auf den eines Rechtecks zurückführen. Genauso wollen wir nun den Flächeninhalt eines Dreiecks auf den eines Rechtecks zurückführen. Hier siehst du nochmals die einzelnen Schritte, wie du den Flächeninhalt herleiten kannst.
Folgende Darstellung sollte dir den Zusammenhang des Flächeninhalts eines Rechtecks mit dem eines Dreiecks nochmals verdeutlichen.
Drehe an den Schiebereglern!
Flächeninhalt eines Dreiecks
Hast du eine Idee, wie man den Flächeninhalt eines Dreiecks berechnen kann?
Flächeninhalt Trapez - Herleitung
Eigenschaften
Welche Eigenschaft(en) haben die Seiten eines Trapezes ?[br]Kreuze an!
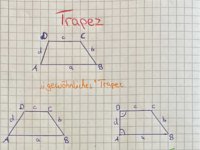
Das ist ein gleichschenkeliges Trapez. Was ist daran besonders? Kreuze an!
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAdsAAAEuCAYAAADGJbieAAAgAElEQVR4nOydZ1RWV/q350PWylpZM5M6ThJTVOzYsaE0aeIDIr2riDQFpClNukjvIKKCCAKCCNKrKNLBGmPsFXtLFLsC1/vhwScyYTIxE8f5z3s+XEtdnrPPPvs5+/z2ufdd/gQAT4FLwAEBAQEBAQGBP5g/AQhiKyAgICAg8PYQxFZAQEBAQOAtI4itgICAgIDAW0YQWwEBAQEBgbeMILYCAgICAgJvGUFsBQQEBAQE3jKC2AoICAgICLxlBLEVEBAQEBB4ywhiKyAgICAg8JYRxPYt0NfXybNnLXR3N9Dd3cCjR408fdrCy5ft/1a7z5610t29/7U2m39Xm319nTx/3srjx008eNDA3bv1PHjQwPPnbe987P6xny9etPHkSRPd3eJ+3r+/j2fPWt953/4VL1+28/BhI3fu7OHx4yZ6ezt+03k9PT+f9+hRI729Hbx82cajR408eNDAw4f7efy4iRcv2ujr63zn9/lH8OJFG93d+7l9u+6NuHt3Dz/9uJcHDxp49qzlf2Y8BP43EcT2LdDb28G9e/VcuFDCxYulXL1ayZ07e3jypPl3t9nX18lPP+7l4sVSLl4s4erVSm7fruPx46Y3bqunp53u7gZu3Kjm/Plivv8+j/Pni3nwoOGdj90/juPDh/u5ebOGCxdKOH48nzNnivjpx73vvG//iidPmunqKue773Zw7VoVL178toXM06ctdHVVcPRoLlevVvL8eSuPHjVy9Wol588X09VVzo0b1XR3N9DT8+8t3v5bePSokYsXSzlyJPeNOHYsj5MnC7hwoYS7d+t/84JGQOBdIIjtW+Dly3bOndtNff1G9u1LpaNjG6dO7eLu3T2/u83e3g4uXChh375U9u5Npb19GydOFHDnTt0bt/XsWQtXrlRw+HAOtbUbyM1dT23tBq5cqXjnY/c6L160ce1aFd99t4P6+o3k5YVRWZnAhQsl77xv/4p79+ppbk5n+/Zg2toyuHNnD8+etdDTM7gg9PS08/RpC9evV9PYuIXMzCA6OzN5+LCRmzdr6ezMpK5uAy0t6Rw5kiMR4nd9n38EN2/WsG/fJjIyAt6InJx17N4dxZ49KZw5U/SbFzQCAu8CQWzfAs+etbB3byqhoY6Eh69iyxZfqqoSOXeu+He3+fJlO/v3byEiwpmwMCc2b15LeXk8Z84UvXFb3d37OXAgi5ycEAID7TA3FxEYaMeBA1nvfOxe58mTZo4ezWXnznDWr3fA0lIbT09LGhu3vPO+/SsuXCghKWkNhobqxMa60dmZybVrVf/UEvHwYSNdXRXs37+F0FBHDAxUSU/35+bNGk6cKCA93Z+gIHuSkjzYsWM9hw5l8/Bh4zu/zz+CH37YSUSEMzo6894IU9MFODgYs27dSvbsSfm3LEcCAm8bQWzfAo8eNZGVFYSurgqGhuq4OJuRkuLNoUPZv7vNFy/a2LEjFBMTDYyMxG0mJ3v+LoG8c2cP5eXx+PvbIhLJ88UXQxCJ5Ckvj3/nY/c63d37qatLISTEAR2deXzzzVAUFGTYsSP0nfftX3HkSC7W1rp8+OFfMTVdwM6d4Rw7lvdPTeC3b9dx5EgOW7f6s2iREn/5y59xc7PgwoUSmpvTcXdfgpaWIra2+gQF2VNVlcS9e//95vTfQlNTGqamC/jznz8YwAcffMD777/Pe++9x5/+9Cfef//9Af//xRdDmDJlHLq6KmRkBNLd/d+1DSIg8DqC2L4F3obYvnzZTkPDZkJDnQgNdWTLFl8qKxM5e3b3G7cliO3b548U25Mnd7FtWyAhIQ5s3OhFfn4Yhw/n8OjR/8aX7fnzxWRkBODiYibB1lYfMzMRKiqzkJL6mo8//hA5uWmsXGkoOcbT01IyF9rbt/H0acs7vxcBgX+GILZvgbchtr29HZw+XUhlZSLV1Um0t2dw+nTh79oHFsT27fNHiu3t27UcOrS9f68+g2PHxE5X/yt7tk+ftnDzZg3nzhVLaG/PoLg4moAAO+Tlp/HFF0NwcTbj8OEcyTEXLpTQ1VXO9evVdHfvp7dX8EYW+O9FENtfoaeng1u3ajlxooD29m3U1iZTWhpLaWksZWVxVFUlUle3gerqJMrL49m/fzNdXeW/Kra9vWKv4kuXyjhyJIf6+o2SNl+nqSmN06cLuX27jidPmujp6eDIkVyys9eRkxNCVVUiBw5kce1aFX19ndy/v4/Ll8s5ejSXvXtTB22zuTm935u5lKKiqAFiKys7mfXrHait3UBlZSKlpbGUl8dTWZlAS8tWzp7dzU8/7uXpU/G+2O3bdZw4UUBbWwZ1dRsGXKeyMoHa2g10dGRy8WIp3d37JeE63d0NXLlSwbFjeTQ0bBq0n/v3b+bcud1cu1ZFeXk869atlIjtlCljWbvWmrq6DVRVJVJWFifpZ2PjFk6cKODmzVoePmykt7eTJ0+auXNnT/8LfBuVlYlUVMRTVhYnuV5d3QYOHcrm4sVS7t2rp6eng+7uhv7x3EFDw+ZBf+9X51dUJHDkSK7EO7ynp31QsT18OIcrVyq4fr2KQ4eyqapKorFxCwcPbqejI5PGxi2Dim1XVwV79qSQlxdKRUU8jY1bOHeumKdPW+ju3s/Fi6UcPpxDQ8PmAeNYUZFATU3ygN/02LE8Hj1q5OXLdh4/buLWrVq+/z6PPXtSJPdVVhZHRUUCtbXJNDencfhwDl1d5QO+HJ8+beHMmSL27k39xXnV1Uns3ZtKc3M6Z8/u/l0e89evV3PgQBZJSWtQVZ3N0KGfExhoP+hi5eXLdi5fLqejI5OmpjT2799Cff1GqqrE/Wpq2sJ33+3g5MkCzp7dzfHj+TQ2bhn02aupSaKtLYMfftjJzZs1/SFc+7l8uZzjx/Pp6MikoWETtbXJA56B8vJ4qquTqK/fyKlTu3j4sJGennZJ+Nq9e/VculTG4cM57NmTQkVFAmVlcZIxq6pKorMzk3Pnirl9u46nT1t4+LCRY8fyBu3nYDQ2buHMmYHz9NcQh5W18/JluxA29R9AENtf4dmzFjo7M9m61R8fHytMTRewYIEcCxbIIRLJo6+vgrm5CCMjdRYuVMTBwZiamuRfFduXL9s5dWoXFRXxREW5YGmpLWnzdZydzcjOXsfhwzncuCGe9JWViaxevQR398VERrqQnx/GDz/spLe3kzNniqiqSiQ21pXly3UGbdPNzYLS0lgOHcomNzdkgNgOHz4UVdXZmJmJ0NVVZsECObS0FNDVVWb16iXs3BnOiRMF3L5dR19fJ4cP55Ce7oeX1zIsLEQDrqOrq4ypqQg/PxvKy+O4eLGUn37cS19fJxculFBXt4GkpDXY2xsM2k8HByPJl+DOneEEB6+QiO1XX32OouJ0zM1F6OurIBLJo6WlgI7OPBwdjUlL86OjI5OurnJevmzn1q1ajh7NpaAgAh8fK/T0VFi4UBGR6OfrWVhoEh7uRGlpLD/8sJNnz1q5cKGEyspE4uLcWbHCcMDvbWw8n4ULFSXnL1qkRHS0K4cObefGjWqePm0eVGzb2jI4fjyfpqYthIc7YWCghqOjMSEhK9myZS3FxTGDiu3Ro7nExbnh7GxGSMhKNm9eS0vLVrq7G7h0qYyysjgiI51ZscJwwDhqaythYjJ/wG+alOTBlSsVPH7cxLVrVXR2ZpKc7MHSpQsxNFRDU1MBTU0FFi0SOyC5uJgTEeFMTU3yAM/3O3f2kJu7HisrHQwN1dDSUkAkUmDRIiWMjNSxttbFzc2C/Pxwrl2reuO59yZi+/hxEzU1yfj52eDibIaDgzFWVoswMFBj4UJFVq0yJS7Ona1b/cnLCyU11RsnJ5NBnz1j4/l4eS3rN01n8PhxE5culVFdncTGjd74+9tiZ2eAqekCNDUVJOdpaSlgaKiGldUiMjMDuXxZvDjp6eng4cNGfvhhJ5WVCURGOrN06UIWLZqHpqYCIpE82tpKGBio4e9vS0FBOIcOZXPnzh66uipISvIYtJ+D4eRkwo4doa/N018f4xcv2nj8uIknT35fvL7AmyGI7SD09HRITFv5+WE4OBgjEskzadIYpKS+ZsyYEUhLj2TcOCnGjBnOV199wUcf/ZWZMyeydWvAoGK7YYMn7e3b6O5uYM+eFMLCHDE3FzF9ujTDh3/F6NHDkJaWYsSIr/j88yHIyU3D1dWc3Nz1HD+ez4sXbeTmrsfIaD4GBmqsWmVGYuIaWlu38vhxE3v3biQ83AkLCxEzZkxg+PCh/W2OZMSIr/niiyEoK88kLMyRwsJIUlK8BojtkCGfMW6cFNOnSzNlylikpUcyatQwvv12KMrKswgMtKOqKpETJwp4+rSZ0tJYnJxMUFefw9Sp45CS+kYyLtLSUowbJ4W2thLx8e60t2dw8WIpT54009KSTny8O8uX6zB37lSGDRvKqFGv+vkVQ4Z8xqxZE/Hzs6a4OJpNm3wICrKXiO1nn33C6NHDmT59ApMnj2X8eClGjvyWb78diqzsZFyczdixYz2HD+fw5EkzJ08WUFAQwdq1y1mwQI4RI34e6zFjhjN8+FdMmTIWY+P5BAbaUVGRwO3bdRw4kMWmTT7Y2uojIyPNBx+8z/DhXzFjxkRkZKQZP16K4cOH8ve//42///1vWFpqs3t3NCdO7OT+/X0DxNbISJ3t29dRXh5PSUkMyckeGBvPR0rqG+bPn4OTkwkxMa4UFEQMKrZNTWm4uVkgEilgba1HQIAdpaVxXLtWRXv7NsLCnDA0VENWdjLffPMlI0d+w/jxUkhLS0nGZ8iQz/jTn/6Eo6Mxp04VcudOHYcObSc7ex3W1rqMHTuCsWNHMG6c+LwJE0YhIyONsvIs9PVVSUxczQ8/7OTevb3cvl3H0aM78PFZzvjx4nEcP158zsSJo5k8eSwyMtLMnj2ZwEB7vv8+n+fPW98oDvZNxPbBgwa2bg1g4UIl5OSmMWPGRCZPHsu4cVKMHTsCLS0F3NwW4+OzHB+f5djZ6aOgIMPXX3+BlJR4rEaPHsawYUMZN24EamqzsbXVY+fOcH76cS/Hj+8kPd0fZ2czNDUVkJYexdixI5CS+oZRo4YxbpzUgHFwd19MU1Maly+Xc+9ePV1d5ZSVxbFu3UrJnJeWlpLMlbFjRzBmzHC0tZXw8lpGfn4YZ8/u5uzZ3QQG2vUfN5DRo4fz+ed/409/+hN//etf+OyzT1BVnU1CwmqOHMnl+vXqf/m1+vy5OFnK48dNgtj+BxDEdhBerWZbWtJZt24lamqyiERymJuLcHY2IzjYnuhoV5YuXcj06RMYNmwoH3/84a+KbULCavbsSeHs2d1s3OiNoaEa2tqKGBvPx9ZWHz8/G+Li3LC3N0RFZRaKitOZP38OK1caUVmZMKjYxsa6UVubzMWLpWzc6I2engoaGnMxMFDDxkaXtWutSUhYjYODcf89yGNltQh398V4e1sNEFspqW/Q0lLA2dmMwEA7EhPXYGdngLy8DKqqs7Gx0SMqyoXKygQuXy4jNdUbbW0lVFRmYWEhws3NguDgFSQmrsbR0RhV1dno6MzDz8+GHTtCaW5O49KlMrZvD2bZMm20tBQwMlLHymoR3t7LiI93x97eEDm5acyZMxVT0wW4uy/Gy2sZfn62ErH99tuhzJ8/B0dHY7y9rQgLc8LOTh8lpRkoKMiweLFmv7duInfv1lNTk8zq1UtYtEiJ+fPnoKYmi729AdHRrgQE2GJvb4CRkToikRwaGnOJiFjFwYPbqalJJilpjURsP/zwLygoyODibIa3txVeXpbY2uqhpDSD0aOHY2YmIilpDfv2pXLjRo1EbP/617+wcKEiCQmriYx0xsHBCAMDVUQiOVRUZuHhsZRduyLYsyeF+vqNv1lsc3PF4T87dqxnyZKFyMpORiSSx8JCE3f3xURFueDhYYm2thKTJ49h6NDPB4jtmTNFZGYG4eJihra2EhMnjkZPTwUfHyvWrVuJj89yHB1N0NGZx4wZE1i1ypTCwkj27dtEWVkcmzevZenShYwdK15U+fvbEhXlgr+/DQ4Oxqirz0FK6htWrDCkvn4jt27VvlFozr8rtgoK0zEx0cDV1ZyQEAdSU33w97fB1HQBIpHYGmFsPB9XV3NiYlzx9bXGymoRCxcqoKAgg5zcVBISVnP7dp1EbB0cjFFUnM7XX3+JktIMbGz08Pa2IiLCGX9/W7S1lRg7dgSmphrExLhSVBRFR8c2Gho2ERBgh7q6LHp6KixZooWLiznr1zsQHu6Eo6MxurrKaGoqMH/+HDw9LWlqSuP69Wr27EkhMXHNL/D3t2HevJm8996f+PrrL5GRGY+dnT7FxTHcuFH9m8LCeno6eP68lRcv2oSEIP8BBLEdhHv36unszGL79mCWLl3I8OFfsWCBHFFRLuzbl8rly+V0d+9n0yYflJVnMXLkt3z66ce/KrYxMa7s3h1NS0s67u6LGTNmOEpKM/DxWc7u3dGcOlXIs2etlJXF4eJihorKLL755kumTh1HaqrPoGIbFeVCYWEknZ2ZuLqaM2zYUGRkpHF3X0xhYSQnThTQ29tJdXUSq1cvRl9fBUXF6f2ipDVAbKdOHYeLizm7dkXwww87gQMUFkZhYaGJurosmpoKWFpqk5LiycGD2wkIsGXatHEoKc0gPHwVLS1buXy5nN7eDoqLY1i6VBtdXRUcHIwJC3MiPz+MAweyCAqyZ/p0aWbOnIiLixl5eaEcO7aDly/bKS+PZ/lyXRQUZJg9ezJz507F1FSEj89yidiOHy/FihWG5OaG0NaWwe3bdRQWRrJ8uW7/gkIBCwsRGRkBXLlSQVqaH0pKMxg1ahhqarNZudKIoqIoHj7cz7lzuykri8PPzwZ5+Wl89tknLFmiRVFRFHl5oURHu0rE9tNPP2bxYk0KCyNpbk6jszOT4uJoHB2NmTlzIkZG6nh4WJKXFyrJhiQW2z+jqjobf39bli3TZtw4KT7/fAjy8tOwsdFlx45Q7tzZ86sOUoOJ7ebNa6moSCA01JHZsyfxzTdfYmGhSUZGAG1tGXR3N9DWlsGaNUuZM2cKw4d/NUBsOzoy8fCwRFFxOrKyU5CRkcbPz4ajR3O5fLmMgwe3k5cXypIlWv0OdAqEhjqQkLAaPz8bbG31UVeXZfTo4Xh6WnLiRAH37tVLTP+mpgv46KMP0dNTIS8v9I0zf/07Yjtz5kQWLVIiMtKZvXtTJQQF2TN37lQmTRqNpeVCkpM9aG5O49GjJk6e3EVeXihubhbIyk7ms88+wdt7GdeuVUnE1t7egOnTJ/DRRz9vDXz/vdjp7eTJXXh6LmP06OEoKMhgaqqBr681OTkhbN3qj7a2En/+8wcsWCBHZKQzdXUbuHq1klu3aikri8PX15oFC+T4/PMhLFggx65dEZI0lP94v319Bzh9uggnJxPee+89yUIpKsqFI0dy3/n7U2BwBLEdhJs3a6mv30hCwmqWLl3I1KnjWLZsEQUF4ZKXxuPHTRQXx+DkZMK8eTP46qvPf1VsXyWiyM5ex9KlC/nmm6HMni02e27evJaSErFTVFqaHx4eS9HUVGDEiK+YMGEU4eFOXLhQwsaN3ujrq0rEdv16RzZt8iEvLxQbGz1Gjx6OhsZcNmzw5OjRXG7cqKGvr5MTJwrYvTuaLVt8iY93JyzMieDgFQPEVk5uGrGxrhITFBygpiYZd/fFGBvPZ9EiJRYv1mTrVn8uXSojPNxJYm42MdEgKMietDQ/qqoSSU31Zs2apfj6WpOe7k95eTzFxTHs2hUheZmJRPIkJLhz6FA2165V0dvbwfHj+eTkhBAX505UlAthYU6sW7cSf/+fv2xlZKRZt24lBw9u5+LFUh4+bKSuLgVvbytMTDTQ0ZmHoaGaxJwWE+PK7NmTGD78K5SVZ2Jrq09i4hrJF1pamh9ubhbMnj2JTz75CF1dZTZs8CQlxYvQUCccHIxRVp6FtLQUnp6WdHRs4/z5Yi5fLqOxcTOenpbIyU3D1HQBnp6/FNsPPvgAaWkpRCJ55OVlGDnyG6SlR2JtrUtGRgAdHZk8etT4RmLr729LbKwb6en+eHktQ0FBhmnTxuPlZcn+/Zs5e3Z3vwl9F2lpftja6jNz5sQBYrt//2asrXWRlh7FjBkTUFSc3r/HGkZlZSIFBeEkJKzGyGg+3347FEXF6djY6OHltQx/f1s8PJYiEikwfPhXaGsrsX69I1u3BpCZGcjmzWvx9LTE2Hg+kZHOtLdv+4992WpozGXRonk4O5tJRP4VVVWJxMS44u9vQ2ysK1u3+lNSEkNTUxp5eaEEBdljaqrBxImjBxXbVatM0dCYy8SJo/H0tKS1NYNr16p48qSZCxdKiI93RySSRyQS73vb2upLnmNV1dl88MEHqKjMwt/flszMQKqrk6irSyEtzW+A2KqozCI93a/f12HfgHu9erWSvXtTiYtzR19flaFDP0dHZx7h4auoqkri8uXyd/7+FBgcQWwH4erVSoqLYwgIsGPp0oUoKc3A29uKzs5MiTPBs2cttLVlsHGjN0uWaDFq1LBfFdvAQHvWr3dg3bqVaGoqMGTIZ0ydOg5ra13Wr3ckKsqFuDh3QkMd8fW1xsBAjZEjv2Xs2BESs1J4+Cp0dJQlYhsYaMf69Q6EhTlharqAiRNHY24uoqoqkUePGiWFBR4/buL27TquX6+SeALn5YUOENv58+dQUBDOw4eNkpCS5uZ0IiOdsbMzQE9PBTMzEbm563n8uImEhNVMmjSav//9b0hLS6GoOF1i+g0MtCM62pW8vDCOHMnl8uVyKisTiY52xdpaF3l5GSwsNCkpieHhw/08f95KX5+4nzdv1tDVVcHly+WcPLmLwsLIAd7IcnJT2bo1gIcP90scUDo7M4mPX83KlUYYGoqdYkJCxFmF/P1tmDx5LF999QVKSjNYvlwHT09LoqNdiYpyYf16R+ztDZGRkeajjz5ETU0WX19rQkIcCAy0x8XZDD09FVRUZpGYuIarVyt5+rSZZ89a+P77fNatW4my8iwsLDTx8lr2C7F97733+PjjD/niiyF89dUXfPutOHwpJsaVs2d3c/t2HS9ftr+x2AYHryA01BFHRxPU1GRRV59DcrLY+emnH/fy8mU7N25U09SURnKyB5qaCrz33nsSsa2tTUZPT4UvvhjCtGnj0NRUwM5On3XrVhId7UpEhDM+PlZoaysxcuS3yMhIo64+B0tLbQID7QgLc0JHZx5Dh37O2LEjmDNnCnp6Krg4mxEZ6UJKihdZWcE0N6dz82bNG5sqf6/Y6uurYm9vSGysG62tW3nypFnC3bvi/dNjx/Ik3t3p6f4kJq7By2sZ5uYiFBRkGDHi60HF1t19MebmIrS0FEhJ8aSrq0KyF33tWhX5+WG4OJthbDwfRcXp6Ogo4+pqgYuLOXPmTOGDD95HXl4GNzcLwsKciI52JSbGlfXrHQeIrby8DLGxrhw6lC1Z+L6iszMLf39bFiyQY+7cqUycOBp398Xs27eJq1cr/2dir/8XEcR2ELq6KigoiMDb24qlSxeirj6HoKAVHD++U3LMixdtHD+eT1FRFKtWmSItLfWrYuvvb4u/vy1eXlYsWCDH0KF/R0ZGGisrHcn/vY6VlQ4KCjKoqMwiNNSRpqY0IiIGiu2rY319bTA2no+MjDS2tno0NaUNuJ/nz1t5+HA/jx418uxZCzdu1FBWFvcv42zb27eRkLAGJydT9PVVMTVdQH5+GD09HezeHd2/EJmOnNw05OSmoao6m4ULFVm8WBNnZ1Oio10pK4ujtTWD7dvXERRkz+LFWsjJTcPSUpva2g2Djn9PTztPnjQNGvozWJzt4cM5pKb64OJshpHRfEQiBQICxM5O3t7LmDBhFF9//QVqarKsXGmEu/tifH1tJOPn6GiChsZcpkwZi5mZiPDwVURGuhAcvAJXVwtMTDQQiRTYssWXe/fqJdc9fbpI8tWyeLHWPxXbTz/9iKFD/87XX3/BV199wdy5U4mMdObUqV3culXLixdtbyy2r3jlKa2rq0xWVlD/IquV3t5O7t7dw9GjO9i+PRh9fdUBYltVlYiWlgKfffYx06dLY2KiwcqVRvj6WhMYaI+vr7Xk3hUUZBCJ5DEymo+7+2LS0nzZtSsCL69laGjMRVFxOnPnTkVVdTZGRurY2Rng4bGU9esdKSqK4vTpwv6qUr89Lvj3iq2x8XxcXMzZtGktR47kSkJvnj5t5sKFUpqa0igoCCclxYuQkJX4+dng4WGJra0+BgZqyMvLMHz4V4OKrYeHJdbWupiZicjKCubu3Z+fhRs3aigpiWXtWmtMTRcwa9Yk5s+fw4oVhqxcaYSs7GQ+/PCvyMvLDHgfvMLPzwYTEw2mT5fGyEidzZvXSqxTr8bj8OEcNm/2xcxMxJw5U9DRmYetrT5ZWUFcuFDC06fN/zPFKf4XEcR2EH6r2J45U0Rd3QY8PCyZOHH0bxJbb2/x18KoUcOQk5uKjY3eoGLr5rYYa2tdXPpDgL77bgfx8e7o6akMKrampiJmz57MypVGtLSkD7if+/f3celSGV1dFdy9W8/ly+UUF0f/W2J74kQBRUVRREW5sGqVKQYGaqipyTJjxgRmzZrEnDlTWLRoHq6u5kRGOhMS4oC/vy3m5iJmzZqEmZmI6uqkQcf/6dNmbtyo5vvv8ygoGBj683vFdtiwoSxcqIiHx1K8va3w8/tZbD09LbG3N8DSUpvg4BXk5ISQluZHePiqf1ts33//fYYNG8rMmROYOHE0Q4d+jrT0SFxczCTe3U+eNP9usXVwMO4P8dEgLy+MFy/a6OnpoK/vt4ntkCGfIic3DRsbPVavXkJIyMp+BykrXF3NcXAwFj+HLmb4+dmQluZLS0s6p04VUlYWR1ycG56elixbtgg9PRXU1ecgLy/D3LlTmTNnCm5uFpSXx3P27G7u39/3m+fgHyW2vb2dPHrUyMRESo4AACAASURBVK1btRQXR+PkZNJv6pVHU1MBU1MNbGz0sLJahJmZiPnz5zJ69LBBxdbTcxkrVhiybJk2ubnrBzwLr4utkdF8pk0bj7LyLOzsDHBwMEZeXoa//e1T5s2b+U/E1hZnZzMsLbXx97elrCyOs2d3c+9ePX19B2hsFFu2li1bhJqaLKqqs/H1taaqKpHvv8/nwYN9krjed/3+FBgcQWwH4cqVSoqKovHzs2HJkoUSR6YDB7b3V25p58WLNslLy919MRMmjPpVsQ0IsCMoyB5/f1sMDNSQlh6JsvJMVq0yJSJiFdHRrsTHuxMd7Up4+CqCguzx8lpGaKgjFRXxnDu3m5QUrwF7tgEBdgQHr2DdupUsXqyFrOxk7O0NaWjYxPPnrZKX7rVrVRw6tJ329gwOHtxOU9MWtm0LfGOxNTHRIDt7HQ8fNnLpUhkHDmRRWhpLSooXPj5WLF6shbLyTKZPl2bMmOFMnTqOBQvksLTUxs3NgtBQRywsNJk2bTx6eirs3h09oM7vs2ct3L+/j4sXS2lrE2cQSk0Vh/7o6iozbJh47zAv79fFVlNTgaCgFdTWbmDtWmsmThzNiBFfY2CgRlDQCsLDVxEX50ZcnDuxsW5ERKySLIRSU32orEwkN3c90dGu/7bY/vnPHzBlyliMjNSZP3+OJLTG3FxEXJwbe/emcu9ePTdu1HD4cPZvFtvAQHuCg1fg5GTCwoWKGBiokZ29jidPmiW1bm/cqKGlJZ2UFC+0tAaakaurk1i0SIkvvhjCvHkzcHQ0JjDQnpQU8X51VJQLQUH2rF27nDVrlhISspKkJA92747m2LE8rl6toqMjk6KiKLZs8SUy0hlXV3OMjNSZO3cqUlJf8/7777NggRzJyR60tWX8wiT6a/xxYtvB3bvipCaxsa7MmDGBv/3tE6SlR6GqOrs/ltgMF2czVqwwRF9fFWnpkXz22cesXr2E8+dLOHQom02b1rJmzRJsbPSwsNAkMzOImzdrJHPs+vXqfp+ExejpqfSb3WVxcjLB1dWcefNm8sUXQ9DQmIuPz3KiolyJjXUjLs5Nsq/r52eDu/sS4uPd2bs3lQsXSrhypYIbN6rZvHktOjrKyMuLrV1LlmiRm7ueBw/28fRpi+BN/H8AQWwH4fr1aqqqEomIWIWZmYgpU8Ziba1LSUlsvyey2EuwuTmdhITVmJqKGDny218V26CgFUREOBMZ6YKJiQZjxgxHXX0OgYF25OeHUVOTTGvrVsmLPjx8Fba2+jg6mlBQEEFXVwWbN6/FwEBNIrbBwSuJjXVj40ZvrKx0mDJlHKamCygsjOTGjWoePWqkr6+T06cLqaiIJzXVm4AAW1xdzfH0tHxjsTU0VGPDBk9OntxFUVEUQUH2hIY6kpcXyp49KRQWRpKREYCPj5UknEZLSwETEw3Wrl3Otm2B2NsbMGHCKFRUZpGa6s358yX9q/dOurrKaWxMY/v2YImQrF69BD8/G/T1VRk58ltUVWezc2f4gH7+o9hqaSkSHr6KtrYMQkJWMmXKWKSkvsHUVIPoaBd27AilsXELzc3pNDRsIj8/DH9/WywttQkNdaKwMIqsrCAiI13+bbF95Y0cEGDL6tVLMDQUWwC0tZUwNxexefNazpwp4vz5EkkCld8itqGhjsTGuuLsbIaCggxz5kwlImIVZ84USUzTZ84UsX17ME5OJsyZM2WAg9SePSmYmGggJfU1KiqzsLHRIz7enfr6jXR2ZtLcnE5ZWRzh4atYvFgLZ2cz1q1bycaNXuTlhVJYGEVi4ho8PS1JSvLoz7CVRH5+GDExrmhqKvDXv4rDpfz8bCgtjeX8+d9eGvGPEtuennauXavi6NFc1q93YNq08YwaNUzioFZQEEFVVSLZ2esID1/F8uU6TJs2nk8++Qh7ewOam9Oprk4mJsYVBwdjyf59dLQrp08X8vDhfl68aOPy5XK2bPHF1FTEwoWKKCnNwNR0gWRRJBLJ8eWXQzA2nk9qqjfl5fE0NGxi/35xJqvMzCB8fJZjaKiOq6s5RUWRHDqUTXV1EllZwdjbGzJt2njk5WVwcDBi0yYf2tu38exZi5AB6v8IgtgOwq1btTQ0bCI52QMTEw2GDRuKtrYSqaneHDiwnRs3aiTeyI6Ov80bOSTEgcTE1Wzc6I25uQgpqa8RieRJSlpDR4e4/FpPT4ckvjc+3h1DQzX09FTIygri1q1atm71x9DwZ7ENDXVk8+a1FBSEY2enz9ixIxCJ5Nm8eS0nTuyUZHs6dCib9HQ/Vq40ZObMiYwaNQxdXeU3FltdXRVCQx3Zs2cjvr7WyMlNw8JCk9raZPr6xAXu+/o6aWpKIzTUESsrHRYtmseiRfNYt24ltbUbcHOzYMyY4cjISBMUZE9Ly1YuXSqjt7eDQ4eySUnxwt7ekHnzZjJx4mj09VUl4j1unFR/WETkgH7+o9guXKhIXJwb33+fR0yMKzIy0owc+S0WFiJSUjwljjPPn7fS3d1AR0cm/v62aGjIsWbNUnJyQkhP9yciwvnfFttXGaTy88PJzl5HcPAKli1bxLx5Mxk/XgoPj6W0t4szS7W2ZvxmsY2OdmXz5rW4OJv1Lya+xtnZjL17UzlzpognT5o5eHA7gYHi+M4xY4YPENuGhk0sW6aNtPQo1NRms2SJFtu2BUqyPfX1iQUvOdkTNTVZTE1FuLsvGWB6X7xYCxWV2URFuXDuXLHk9+/qqmDNmqV88slHzJgxAXt7A9LT/Qdsw/wr/iixffmynYsXxXu1vr7WTJ48llmzJpKRESDpb19f5y9Cfz7++EPMzUXs2hVBdvY6goJWYGmpjZLSDKSlR+LpaUlnZyY3b9bw9GkL584VExXlgrLyLDQ0xNm7nJxM2LDBk6SkNejqKvPll3/HxkaPysoEzp0rpru7gUePGjl1qpC6uhQ8PZcxe/YkDA3VSE/3o75+I7Gx4nh+WdnJDBnyKQoKMiQlreH48Xxu3ap95+9Kgd+OILaD8PDhfsl+rKurORMnjpYIyytP1tRUn36hnYm0tDh2cu7cqWRmBg4qttHR4gxB+/al4uGxlKlTxzFnzhTMzER4eS0jKcmDnTvDiYtzY/XqxVhaarNo0TyWL9ehqCiKBw8ayMwMwtBQ/bU4W3Hs7qFD4rjXmTMnMnfuVJYuFcfQpqR4UVAQQUiIA0uWaKGrq8yiRUoYGqqxYoXRG4utgYE4pObVV4Ks7GQUFaezZs1Stm0LJDd3Pbt2RRIYaIe+virz589BW1uJ5ct1SEvz44cfdhIZ6cKcOVOYNGkMenoquLsvJi7Orb9mrTir1sKFihLvZwcHY3x9rd/oy1ZbW4mkpDWcOVPEtm2B6OoqM2PGhH7RWEBAgC05OSHs2LGebdsCCQ11xNR0AfLyMgQE2NHUlEZ5eTwJCav/MLHduTOc6uokiotjSExcg4mJhiQBQlSUCzk5IVRUxP/mONutWwOor99IcrIHWlrirEZaWgqsWmVKcPAKUlPFqQUXLVJCWnokX3759wFie+RIDqGhjujrixNsKCpOx9ZWj7g4N0lx9rg4NywsNJGWHomhoTrr1zuycaM3GzZ4EhrqiJmZiGnTxmNhoUl8vDs5OSHk5ISQnOyBtraSJBHIf8uXbUjIL79sc3JCKCiIICbGFTs7A1RVZzNy5LcSsS0oiCA3dz1hYU4sX67L3LlT+frrL9DSUiAgQDzHsrPXkZzsibm5CGnpUejpqeDtbUVami979qRQWhqLra0+I0d+K0nIEhrqyNat/mRlBRMW5oSTkwl6eirMnj0Zc3MRaWl+lJTE4O6+GFnZKYwfL8WXXw5h5syJODoas2GDJ9u2BbJrVyS7d0e/lhu5iLt364Xavv+FCGI7CD09HTx50kxXVznR0a7IyU2TpL0bN07sdayoOJ0JE0b1pzr8lL/97RMUFaezfXvwoGIrDqBP5/r1ahIT1/SvkKUYNWoYEyaMknw9KCnNYOzYEcjISCMSybN69RJqazfw9GkLOTkhA5JaJCSspqkpjZ9+3EtqqjdqarJIS49kzJjhTJgg3pMyNxehqDidkSO/Yc6cKaxYYdgfv7rijcXWyGg+aWl+XL1aSWysK7NmTURK6htmzJiAurosOjrKkutJSX2NtPQotLUV8fS0pLw8ngcPGti+PZiFCxUZP15872PHjug3uYmYN28mo0YNQ0ZGGmtrXYljVUCA7Rvt2WprK5GS4iXJG+zqao66uiyTJo1h2LChzJ07FWPj+Rgbz0dHR1ni2DV9ujQREau4fLmczs5MUlN9/lCxPXhwOxculNDSko6LsxmjRw9j7typ6Oqq4OFhyfbtwb9ZbIuLY7h8uZyammRWrjRixowJktScU6aMRV5ehunTxWk7P/nkI/7ylz8PENsLF0ooLIzE19cabW1FRoz4mkmTxiAvL4Oy8iyUlWchJzeNMWOG88knH6Gjo0xqqjclJbEUFESQkuKFqekChg8fypQp41BXnyOxYmhozGXcOCk++OB9ST7m1tZ3v2cbE+PK9OnS/O1vn0jmh7a2EqamItTVZSWL5o8++usAsc3LCyM62hU7O3G88ocf/gUpqW+QlZ0sydimra3EpEljGDLkM8zNRezYsZ6DB7dz9WolR4/uYO3a5UyaNEby3E+fLo2WlgJ6eqrIyk5BSuprJk0ajazsFKysdNiyxZecnBDMzEQMGfIpX375d779diiTJ49FXX0ORkbzMTVdgLm5JsuWLcLOTl/i33H2bNHvqgYm8HYRxHYQenvFacxu3aolMzMIc3Oxl6K8vAzy8tMkmYoUFGSQkRnfnx/5c+bNm0F29jqePm2moiKB1auX4OlpSUyMK7t2RXLy5C6ePWuhqioRDw9x0L+S0gxkZaegrj4HHR1lVFVnM2vWJBYtUsLdfTEZGQEcPZr7q4UIeno6qK3dgI/PckxNNVBWnoms7GTU1GTR1VVhwQI5FBVlWLp0IRs2eFJWFte/GvfA0dEYNbXZODub0dw8MGTo++/zycsLJSLCGTc3C9asWUppaRwPHjRQVBSFvb0BmpoKaGjMRV19DpqaCq9dbzr6+ip4ey8jKyuIw4dz6Olpp7FxC8HBKzA3F6GmJr5XcWpHZUQieZSUxPG6cXFuVFQkkJcXyubNa3FzW4xIJI+1tS41NckD+nnqVCGFhVHExLji5bUMV1cLCgsjuXVLXJpu27ZAvLyWYWIyH3l5GebPF4+1rq4yOjrz0NNTwdRUAzs7A3buDOfevXpOnSpk9+5oYmNd8fCwxMHBmMJCsYWhr6+Tnp52zp8vYetWf4mVIDnZg9raDVy7VsXp04WsW7cSeXkZfH2t2bdvkyQJx6VLZWzc6I2RkTqLF2tiY6NHSIgDRUVRFBVF4eJihpzcNOLi3CRfZf9YiGD//i3culXbvy/tgKGhOurqc5g9ezLz5s1AJJJHVXU2s2dPQlp6JEOHfs6f//wBq1aZcvp0IXfu7OHQoWx27gzDx8cKTU0F1NXnoKw8k3nzZqKiMgtV1dkoK89ESWk63t7LqKpK5NCh7P7qSQkEBdmjra2IlpYC2tpKaGsr9RckkEdNTRYlpRl4eCyloiLhjb2R792r5/TpQnbtisTBwRgNjbls2bKW7u79vzj24cNGiotjWLXKlDVrlkpSJZ4+XTTAG3nXrgisrXVRUpqOktIMlJVnoqWliImJBrq6yqirz0FBQexJraAgg4+PFTU1SezeHU18vDsODsYoKMjw5Zd/Z8KEUSgqTpcUfNDWVkJNbTZKSjNYt24FHR3buH69midPmrl2rYqcnBBJvLq8vAyKitMRiRRYuFAJZeVZyMpORk9PBUdHE+Li3CSlND08lg74TfX1VbGw0GT5cl1sbPSwszNg5UojnJxMiIx0pro6iXPndg9YFAr8dyCI7SC8eNEmCZcpLY1l/XoHAgPtCAlxIDx8lSQYPTDQDjc3C3R05jF+vJREbF+8aOP77/PYtSuCoqIoSQm3GzfE3ouXL5fT1pbBzp3hREf/LBBOTqa4uYnzFqekeFFbm8zJk7u4c2cPPT0dHD2aS3Z2iKTE3sGD27l+XVxi78qVCjo6trFrVwSxseI23dwscHIywdfXmuhoV/Lzwzh4MIuzZ3fT0SF+YWZlBRET40peXugvCtFfu1bFgQNZVFYmSkyER47k8Px5K6dPF1FTk8TWrf6Eh6/C09Oy/x5MWLt2OVFRLmzfHsy+fZskL/dXXpsHD25n9+5oEhJW4+1thZvbYpycTPHxWU5kpDM5OetoaxMXL/juux39sZERJCSsJisrWJJO8hU3b9Zw+HAOdXUbKCqKoqAgnCNHciTJPE6dKqSxcQs7dqwnLs4Nf39xmIWbmwXe3lb91wyhoWETJ0/u4qcf99LVVc6hQ9nU1iaTlxfK1q0BA5KaPHnSzNWrlTQ2biEnJ4TS0lj27UvlxIkC7t/fx82bNVRUiKu8VFQkSFJ8vnjRxk8/7qOjYxu5uSHk5KwjO3sdZWVxtLdn0NaWIXGQ27Mnhfv393HlirjEXn5+KBUV4lKCx47l0dVVIXGqCg5eQUiIA6GhjkRGOhMb60poqCNeXsuwslqErOxkPv30Y1xdzTlzpoinT1u4fbuO06eL2Lt3I1lZQURHu7BmzRJcXMxYs0bsmBYd7Upami/19Rv7a+vWcfNmDRculLJ//2a2bw8mKWmNJJ/ymjVL8fBYSkTEKrZs8aWuLoXz54vfOM72lWf68eM7yc8PIz7enaamtEELxD992sKBA+JF1Y4dodTUJHPkSA43b9ZI4myfPGnmxIkCSkpiSEpaQ0CA+Bnw9LQkMNCOqChxIo7UVG/i4tyIjHSmoCBC4qSUlOSBi7MZCxcqISMjja6uMi4u5qxevQSX/mcpOHgFycke1NencO1alSTB/+PHTZw5U0RDwyZ27Fjfn8VKHN7n4mLG2rXLCQtzIisrmPr6jXz33Q4uXy7n3LliSkpiBvymiYlrSEnxYvPmtWRkBJCdvY7MzEBJNqyjR3O5ebNGSG7xX4ggtoPw7Jm44s+JEwWUlcWRkLCaTZt8KCgIp7w8XlKLctu2QGJixCXtZs6cyIIFcuTlhdLb29H/kt/F6dOFXLxYOugEuHGjhs7OTEpKYsjICJCISXl5PEeO5AwImu/tfRXCk82RI7mcPbtb4nH8epu3btVKQnK2bQskPt6dwsJIDhzI4vLlMkmGqOvXqzl+PJ/Dh3Nob9/GiRMFvzDRPXy4n+vXqzl7togjR3I4fDhHUj9XnCijkfPnS/pfIqGSdJAFBRF0dGzrr2XbMOgY37tXz5EjOZSXx5OVFUxCwmp27gynvT2DCxdKePCggZ6eDu7f38fVq5WcOrWLgwe3c/x4PnfuDDSRvco8dfFiKadPF3Lq1C5u366lp+fncIgnT5q5cqWCI0dyKC2NJTnZk02bfMjJWceePSlculRGX18nz56Ja8TeubOHa9eqOH++mO++20FnZyaXL5fz4kUbL16Iq6XcuVPHxYul/PDDTs6e3c3ly2XcubOHZ89aefy4iXPniuno2MalS2UDhOZVfdOurnLOndvNiRM7+5+TEi5cKOHYsTza27dx8WKZpD+XLpVy8mQB584V09VVzsWLpZw/X0xzcxqZmUGSZ6esLF7yjObnh7Fxozdr1y5HS0uBYcOG4u1txblzxZK+vHzZzk8/7uXKlQpaW9PJywslMzOQHTvWU1oaS0eH+L5/+nEvL160Sc7r6WmXLAQOHtxOeXk8O3asJzMziOzsdTQ2buHSJXF94NfPe1O6u8X+EwcOZHHlSsWgSRtevmzvX3hkcfRoLufOFXPzZs0v6ui+qt97/Hg+VVWJbN3qT3Z2MDt3hrF370Z++GGn5Pdub9/G8eP5XLokXlSkpHjh5rYYU9MFqKnJ4upqTkZGAFlZQaSkeLFliy81NUmcOLGTGzdqBr3nn8PwsqmsTGDrVn9SU30oLo6WLC5fz4UsTsRRQmtrxi9ob9/G4cM5kjnc0bGtPySrUpKV7V2/RwUGIojtILz6ajlwIIuEBHdMTTWwtdUnOHgFSUkeEicRFxdztLUVUVWdLUkFWFERT19fJ48fN3HnTh137uzhpx/38uhR4y8m4KNHjVy9WsnJk7s4fDiHtrYMjh7N5fTpQokJ6tWxfX2ddHfv59q1Kq5fr+bu3fpBJ9WjR01cvVrFqVO7OHIkh9ZWcSHsq1cruX9/X3/8rbgg9q1btVy/Xs2VKxWSgtWvt/Uq89Tdu/Vcv17N9evVPHwoNuO9qhjy0497uXixlGPH8jh4cDutrRkcP75TkjbwVdH4wcb4+vVqTp8u5OjRXEmt15/Pa3lN/Bq4c6eOa9equHWr9hcv0Vfi99OPe7lzZw937oiLuL8eDvHiRRsPHjRw40Y1J0/uoqNjGwcOZPHddzs4f75YYuLs6Wnn+fNWnjxp4uHD/ZIY2KtXK/sTB3TQ29shqQX60497uXWrlrt367l/fx9PnjRJ4rDv3avnyhXxuL8u/L29HTx92syDB/u4d6+e27d/fk5++nEvN2/WcOVKBffv7+PlS3F/7t/fx+3bddy7V8+DB+IFyOnThRQWRuLuboGpqQarVy8hIWE1GzaIFxIhIQ5YW+uipaWAurqsJE3k6/lzxX1p4cGDBkkqwyNHcjh2LI+TJ3dJ+v/0afOAWM7e3k7Jea/M5q/O/e67HVy6VNY/Hs0D7v1Nef68lbt393D1ahUPHjTQ2/vLEJfe3g4ePGjg6tVKbtyo4d69+kHn26vn5NatWs6cKeLQoWyOHs3l++/zuXChhFu3arl3by83bojH/9atWu7f38eBA1mSrQxT0wXMnz+XkJCVNDenc/RoLh0dmRw8uL0//WYtjx41Dhr3+vocPn26iMOHs+nszOLEiQK6uir46cd9A0rdvVoIdXVV/IIrVyq4fr16wBy+ebOG7u4GSYz9u36PCgxEENtBePy4iYsXS9m/fxMuzmaMHPktM2ZMwNxcJDE9enpaoqo6m88++4QxY4YjEing52dDY+MWSTvicJhfv9br4Qf/yK8d/3va/OVxrx/72/r571zv3znv577+69/v1475PX19de3fe73f0t/X2/hn13t1TF9fp+QLLSXFCw2NOYwc+S0ikTwuzmZ4eCzFz88GS0ttZGSkGTHiKxQVp7NkiRaZmUH/1FHpP/E7/l7epB+/bbwH6/Pgz9rx4/mkp/tLxFZDQ46NG725dav2n7bxR47Xr70j3mQOC7xbBLEdhFer6VOnxFVTrKx0MDcXYWmpjZWVDtbWulhZ6WBoqMb8+XP6kyGI88CeOlX4zvsv8L+P2MRfRVVVIt7eyzA0VMPcXISV1SKWL9fB2loPU1MRIpE8WloKkvCs9vZtPHgwuGlfYHDOny+mpCSWuDh3vL2tcHIyobAw8o1KBgoICGI7CL29YqeK7u4GDh7cTn5+GGFhTtjY6KGvryLxPrSz0ycw0I7MzCBaWtK5eLGUBw/2vfP+C/zv09PTzrNnrZw5U0RxcQxRUS64OJthaKiGjo4yWloKGBiosXy5Ln5+NpSUxHLtWhUPHgw0VQr8a65fr6a1dSuFhVGkp/uTlORBU9OW31SgXUDgFYLY/go9Pe39CfHzKS0VJ11fu3Y5Hh5L8fCwJDnZg9LSWA4e3N5f17KJly9/vzOIgMCbcu9ePceP51NTk8yWLb74+dng5bUMd/fFBATYkZTkQVFRFCdOFLzzvv5f5f79fZw9u5sDB7LYv38zdXUbOHWqcNDC7gIC/wxBbH+FV45Od+/Wc/FiKUePir0UW1u30tq6lWPH8rh4sVTitPPyZfugDhwCAm+LZ89aJJ7NP/ywk46OTNraMmhpSaezM5Njx/L6808LJs/fyysHtVu3arl2rYquropfOL0JCPwrBLEVEBAQEBB4ywhiKyAgICAg8JYRxFZAQEBAQOAtI4itgICAgIDAW0YQWwEBAQEBgbeMILYCAgICAgJvGUFsBQQEBAQE3jKC2AoICAgICLxlBLEVEBAQEBB4ywhiKyAgICAg8JYRxFZAQEBAQOAtI4itgICAgIDAW0YQWwEBAQEBgbeMILYCAgICAgJvGUFs3wEvXrTx5EkT3d0N3LtXz+3bddy+XcetW7Xcvl3HnTuv/i3++08/7uXhw/08e9ZKX18nfX0H+v8U867vR0Dg/3d6ezt5/ryVR48auX9/H3fv7uHWrVquX6/i2rUqbtyo4dat2v653MizZy2SEn19fZ309gpz+X8dQWz/w/T2dnD9ejVHj+ZSX7+RnTvD2brVny1bfElN9WbLFl8yMgJIT/dj06a1ZGQEUFISQ3NzGufPl0gm6fPnrf1/b3/n9yQg8P87T540c/FiKR0dmVRVJZKTs44NGzwJC3MkOHgFMTGupKb6UFQURXNzOmfOFPHgQQN9fZ28eNHG06fNvHjRJgju/zCC2P6HefmynWPH8ti5M5zwcCfs7Q3Q11dl4UJFNDTk0NZWwsBADV1dZTQ1FTAwUMPdfTEbNnjS1JRGd/d+Xrxo49GjRrq79/P8ees7vycBgf/f+enHvbS2biUjIwB/fxuW/D/27jOqqnNd+/jHPcYZZ+9z9jn7mHfHZMfYoqLRiF16Z9ERQTooYo00RUVUjL03jIhdVBSxIUVEege7xm4UESsmgvT2fz8QidkxtgAL5f7wG45krTXXPSdMrrXmfJ7ndjFFT28IvXt3o2vXLxg0qA8KhTpeXg58//0MkpI2UlQUR319LhUVGTx7lkxFRQb19dKQ/mMlYdvKamqyyc/fxZYts/HxcUShUGfYsH4oFOrY2xvj7GyCu7s5zs4m2NkZYmOjh62tAQ4OCubNG8++fYvIzt5OYWEslZUZ1NbKN9vWVlqaSkFBNJcvH+D8+XBOn97NjRuHefgwvunDkLJrFK2juDiRS5f2Ex29hiVLpuDubo6LiylOTibY2xv/cg7rzr0b2gAAIABJREFUY2Ojx4gRetjbG+PqasbcuZ5ERCzh9OndFBREU16eLt9sP3IStq2sujqLjIytrFnjh4uLKf369aB7906YmWni6+vM1KkuTJvmire3IxMn2mJvb4ya2jd07vw56uqqODgoWLt2Khcv7qe+PldOTiW4dy+WtLTNHDiwhO3b57JpUwDR0Ws4d24v9+7FUlGRrvQaReu4evUge/cuZNo0VxQKdbp1+wIdnUG4u5szc+Zo1qzxIzh4OoGBHnh4WGNoOBwVla5oaQ1k8uRRbN4cyKlTYdTV5VJfL+fyx0zCtpVVV2eRmrqZZcu8sbU1pGvXL+jS5XPc3c3ZunVOk9DQWQQHTycoaByjRhmiqqrSZMKEkcTGruPx4wTKy+UPe2uoq8ulsDCWU6fCOHx4OatX+zFrlgdTp7rg7e3I/PkT2bhxBjExa7hyJZKff0qisjJT6XWLllFbm0NVVSZpaZsJDPTA1FSDYcP6oaLSFTs7QxYunMTu3fNJSgohI2MLERFLWL3aF0dHBSoqXenXrwcKhQbTprlw4sQGpe+PaHkStq3sVWGrotKVefPGc+lSRJMLF/Zx7txeUlND2b59LoGBHlhaatO9+5eYmGiwdu1UcnJ2cO9erNL3qT2orMwgJmYt06a54uJiipWVDqamGlhZ6WBjo4+ZmSaGhsPw9nJg375FXLiwj0ePTii9btH8GhryKC9P58mTBPbvX4ydXeOHYYVCHQ8PS9atm0Za2mauXInk7t0YioriuHbtEPn5Yaxa5cuIEbpoaQ1EXV0Ve3tjIiOXKX2fRMuTsG1lrwpbVdVehIbOeuXzy8vTuXHjMMnJm5gyxZ4uXT5nyJCvmTrVmQMHlnL58gGl79PHrL4+l6qqTB48OM6yZV6oqqrQq1cXVFVVUFdXRaFQx9JSh4EDe9Ox4yfo6Aziu+8mEBe3nps3jyi9ftESvxN5PHlykuvXD7F27VSGDu3Ll19+hrOzCVu3ziY7eztlZWm/e11dXQ6JiRsJChqHi4sphobDsbMz5MCBJUrfJ9HyJGxb2buGbU1NNsXFJ7lx4zBLlkxh+PBv0Ncfio+PIzt2BHHu3F6l79PH7PnzNK5dO0h8fDCTJ9vRtesXaGioMm2aCxs3zmTbtjls3z6XadNcMTPTxNFRQUDAGHbunMeFC+FKr180v7q6XG7ePMzJk98TEDCab77pSc+enZk50538/F0UFES/cpZAfX0eN28e4eTJ79m/fzFbtsxmz54FXLiwT+n7JFqehG0re9ewbWhoPEkrKzMIC5uPjY0+1tZ6eHk5EBw8nfz8XUrfp4/Zo0cnSEjYwPLl3piba9Ghwz+wsdEjIWED5eXplJen8+xZMidObGDBgkn4+7vi5+fM8uXeZGdvV3r9ovnV1uZw6lQYW7fOxsPDil69utCvXw82bJhOTU02dXW5NDS8+rV1dTlUVWVRWZlBeXk6FRUyo6C9kLBtZe8ati/U1GSzd+9CbG0NUSg0sLc3ZsYMd06c2EB1dRZ1dTkyMrkF3L9/nOjoNXz33XhGjNDjq6864+lpTU7Ojqbn1NbmcO3aQeLi1hEZuZR9+xYRE7OWGzcOK71+0fxqarLJzt5OcLA/zs4mfPXVl3zzTU9CQgKUXptouyRsW1lzhK229iC0tAbi5GTCvn2LKC1NpaoqU6YOtICiojgOH17B7NljcXIyQV1dFX9/N86c2dP0nIaGPJ4/T+Phw3ju3YujsDCWBw/iX3nfTnz4amqyycjYyqpVvtjbG9O9eycJW/FGEratrDnCVkdnMLq6Q3B1NSMiYknTuskSts3v3r04Dh5cTkDAGNzczDE0HM7cuZ6cP//r/diGhjyqqjIpKUmhuDiRR49O8OTJSSoqMoDG2wB1dTm/XF6Un9GH7kXYrl79/mFbXZ1FSUmKTBFrRyRsW1lzhK2pqQYODgoCAz04efL7l+4TyR/y5vY2YVtfn8vjxwlcvRrJ6dNhpKdvIS9vJ0VFcU0/u/Ly9N8sPi8+XC8uI2/YMB0XF9P3uoz8809JXLkSyfnz4Tx8GK/0fRItT8K2lb37AKnGb0VlZWns3BmElZUOVlY6eHk5sGHDDBkg1cKKiuI4dGgFgYEeuLiYoaMzmJkzR5OfH0ZNTTb19bkv3bNdT3j4IrZunU1ExGIuXz5AQ0M+VVWZlJamUF6eLoNhPgK1tTmcPr2bHTuC8PS0RkWlC3379mD9ev83NhR48cHr2rVDxMau5fDhFVy5Eqn0fRItT8K2lb1r2FZXZzV9a1q4cDJDhnyNnt4QfHwc2blz3m++YYnmd//+cY4dW828eeMZOdKA3r274epqxpEjKyksjG26X378+HpmzhyNl5cDvr5OrFrl0zSI6sVqQy/CWdn7JP6curpcbt06SnJyCIGBHvTv34uePbsQEDCGM2d2U1gY84dTf+7cOUZGxla2bZvDtGkusoJUOyJh28reNWzLytK5fv0QJ09uZNIkOzp16sjgwX2YOtWZyEhZ1KKlPXwYT1zcOhYtmoSpqQaffPJ/GBgMZcOG6Zw+vZsHD+IpL08nJCQATc0BDB3aF4VCHV9fJxISfv0j+qIPsbL3R/x5DQ15PH2ayK1bRwkO9mfYsH506fI5Y8ZYsnfvAk6fDnvlMqp1dbnk5OwgOHg6Hh7WDBnSF03NAWzbNkfp+yRanoRtK3tV2Pbq1YWZM0eTk7ODM2d2c/Fi41KN+fm7SEjYQGjoLGbOHI2lpTY9e3bB3FyLDRumc+pUGPfvxyl9nz5mJSUpXLiwjyNHVuDn58SwYf0wMBjK2LHWzJnjyerVvoSEBDBmjCX9+vVAS2sg48fbNP18lF2/aH4NDXlUVKRTXHySiIgl2NoaoKraCxMTDcaNG0FwsD9paZv54YcD3LlzjLt3Y7h69SD5+bvYsGE6rq5mGBuroa6uysiR+kRELFb6PomWJ2Hbyl4Vtp06dcTW1oAVK3zYuHEGu3bNY8uW2axdO5VZs8ZgZ2fIwIG9f9GHyZNHceLEBhnJ2Apqa7MpKUnhzp1j7No1D0/PESgU6gwc2JvevbvRv38vBg7sTZ8+3ene/UusrHRYs8aPtLTNFBREK71+0TLq6nKprs4iJSUUf39XDAyGMWCACj16dGbUKCOWLfNi375FJCZuJC1tM5GRy5qCtk+f7vTv3xjO06a5ymXkdkLCtpVVV2eRmbmVtWun4uZmjqpqL7p374SBwTDGjrXG28uBmTNH4+fnzPjxNowaZYS29kC+/vorDA2H4eZmzoYNM+TysRJ+bjk5O9i0KQBfXycsLLRQV+//C1UMDYdhaanD7NljOX58PXfuRPHsWbLS6xYt6/LlA+zcOQ9vb0eMjIbTteuLFnsW+Pu7smTJt6xY4UNAwGjGjbPB2FgNFZWu6OgMwtvbQZZcbUckbFtZY/P4MLZunYOfnzNmZhqoqfXH0HAYVlY62NoaYG+vYORIfUxMNFAo1LG21sXRsbF5fHj4QnJzd/L4cYLS96U9qavL5f7945w/H05KyiYOH17B3r0L2bt3IeHhCzlwYClHjqwkM3Mrt29HUVqa8spBMuLjUlycyA8/RBAV1TiIzsZGD1NTDfT0hqCrO/g3dHQGN53PM2a4Exm5lEuXIuRcbickbFtZbW0Oly5FcOjQclat8sHbywFHRwUjRxpgaanTxMREAwODYZibazF58iiWL/chLm49hYUxMoVEiDbm0aME4uLWs2jRZNzdLVBXV6V37+507vw5nTp1REWlC4MG9cHe3pjZsz2JjFzGjz9GKb1u0XokbFtZfX0uDx/Gc+nSftLSNhMVtYrw8IWEhc1nx46gJtu2zSE0NJDt2+dy5MhKUlNDuXr1ICUlKTKFRIg2pqwsjatXD5KUFEJExBK+/34GK1b4sHDhZBYsmMiyZd6sWzeVvXsXcOJEMBcv7uPp0ySl1y1aj4StEtTV5VJTk01lZSbl5emUlaXx/Hkaz5+n/kZpaeO/5eXpVFa+mKeZJytFCdHGNDTk/XJOZ1BWlkZpaQrPniXz7FkyP//U+G9JSQplZWlUVGRQXS0fmNsbCVshhBCihUnYCiGEEC1MwlYIIYRoYRK2QgghRAuTsP2ANXYEym0amNE4qCqFkpJflZam/ua/3/axX5+T8rttvv75b97mH73P+7zufetsrW215DZbY9vKeB9lvd+/v/fv/19qU1efxpaWb3eOyoBGARK2H7SammyePDnJrVtHyczcysGDy9i9u3EK0fbtcwkL+469exewa9d3bN8+l23bGr38WFjYbx972c6d89izZ0HTNl/1nJe3uWvXy9t8/fP/7Ov+vc7du+eze/d8du6c986vf9muXY37HBb23Rv3+d23+ebj+K527Ahi9+757Nmz4E/v+5uO8Z4989/qd6G53q+5fqbvejz/6LyJiFhCZuY2bt+O4unTROrqXj/X/cWSjlVVWW98rvj4Sdh+wMrL07lx4zApKaEEB/s3Le9oba2LpWXjalSOjgpsbQ2wsNDGzEwLMzMtLC21f/OYpeWvj73MxkYPe3vjpm2+6jkvWFj8+zZ1Xvv8l183cmTj6+zsDN/6dS8bMaKxTnt7I0aM0Hvn179gbq7FyJH6ODg01mJl9e61vGqbNjaN2xw1yhArq9cfx3dlba3LqFFG2NsbY2Pz/vv+Ju/yu9Acmutn+q4sLXWwszNsWmjm5fNm9GhLgoOnk5m5lR9/jHrjCmE1Ndm/TOtLldXEhITth+zJk5OcOBHM0qVeTJpkh7m5JgqFRtMfYCcnE9zczHFyUjBqlBF2dobY2Rn+22Mmv3nsZQ4OClxczHB2NsXe3viVz3l5m46Oijdu802ve9P7/HGdpri4mGJvr3jn1/+qsRZXV7P3ruVVXmzT2bn5tvmCvb0xzs6muLqaNX1IaAm//V1oufdp/p/pux/PxnPDDEfHxvPGzEwLHZ3BmJpq4OvrRGjoLLKytlNWlvba87OuLofKykwqKjJkxTchYfshKyiIZsOG6Ziba6GvPxQ1tf4oFOq4u1vg4+OIr68zU6e64OvrhI+PI97ejX77mPNvHnuZr68Tfn7O+Pk54+Pj9Mrn/HabTm/c5ptf9/r3+bN1vu223reWlq7v98fv1237+jbvtltrH9rC+718PBvPDeem88bZ2RQ9vSFoaKhiY6PHt9+O4uDBZfz80+tXgHoxpqLx/q7ct23vJGw/QLW1OZSXp3P27B6mT3dDRaUrw4b1Q6FQx8PDmgULJrFp0ywhRDOYO3cczs6mKBTqGBoOQ6FQJzjYn4KCaKqqMqmrk5WgxJtJ2H6ASktTuXPnGDExa3F3t+DTTz9BoVAnIGAM27fPJTFxI2fP7hVCNIOYmLWsXz8Nby8HFAoN+vfvSWCgB6dO7eLRoxPSU1q8FQnbD9DDh/Hk5e0iNHQWZmaa/O1vf8Xe3piIiCVcuhTxxstbQoi3V1QUR2bmNjZsmI6VlQ6ff/4pnp4jiIlZw/XrhygtTVF6jaLtk7D9AN24cZjIyKUEBIxGX38on376CZMnjyIjYwsPHsRTUZGh9BqF+FiUlqZw+3YUUVGrcHe3oEuXz3FwULBx40zS0zfz8GG80msUbZ+E7QfozJk9rFzpg4ODAnV1Vbp3/5K5c8dx69ZRamtzZDCGEM2ovr5x4Zhz5/bi4+PEV199iYWFNjNnjubAgaXcuXNM6TWKtk/C9gOUnr4FPz/npsEalpbabN4cKJ+whWhB168fYtGiyWhoqGJqqoGDg4I1a/y4fPmA0msTbZ+E7QcoPj4YR0cFAwao4OioYP78icTHB8u9WiFa0J07x9i8ORBHRwUmJhqoqfVn2jQX8vPDlF6baPskbD8QDQ35VFRk8PRpInv3LkChUOfrr7vj7eXAsWOruXRpP+Xl6UqvU4iP1cOH8URHryEoaDw2Nvr07NkFFxczEhI2UFaWRk1NttJrFG2XhO0Hor4+j7t3Y8jN3cHSpV5oaQ1kwAAVFi/+lhs3DvP4cQK1tXKyC9FSSkpSOH8+nEOHluPpOYIuXf6FubkmYWHfcevWUbmyJF5LwvYDUVeXy7lze9m9ez5eXg4MHdoXNbX+bN0655fOIsqvUYiPWXV1FsXFJ7lyJZKZM9358svP0NIawLJl3mRkbKGgIFrORfGHJGw/ELW1OSQmbiQoaDxOTgq0tQdhaanN7t3zqazMlFHIQrSwurpcysvTKSqKY+VKHwYP/hpd3cFMmWLP5s2B5OXtknNR/CEJ2w9ETU02ERFLmpaNUyjUGTvWisjIpZSUJFNZmUF9vZzgQrSUhobG2znl5ens3BmEhYU2BgZDsbbWxc/PiWPHVlNSkkJlZaaci+J3JGzbuPr6XKqqsvj5pyQ2bpyBru4QdHUH4+5uwdKlU0hJ2UR5eTrV1VnyaVqIVlBdnUV09Bq8vRywsdFHX38IDg4K9u9fLOei+EMStm1cbW02z54lc+dOFPPnT6B3725oaQ0gMHAsUVGruHIlktraHOrrZTF0IVpDTU022dnbCQ72x9NzBGpq32BoOIxdu+bJuSj+kIRtG1dRkc6PPx4lPX0z3l4OdOnyOQYGQ9m4cSYXL+7n0aMTSq9RiPakri6X69cPER8fzOzZHgwf/g1DhnzN6tV+3L9/nJKSFOkEJH5HwraNKy5OJDU1lA0bpuPkZEKPHp2xtTXg0KHlPH6cIHNrhWhlDQ15PH2ayK1bRwkJCUBPbwh9+/bA28uBo0dXcfHiflmfXPyOhG0bd+9eLHv2LGDChJGYmGjQr18Pxo+3ITNzq9JrE6K9i4pahYWFFr16dcHaWpc5czyJjV3Hs2fJSq9NtC0Stm3crVtHWLHCBz29IRgbq2Fqqsn8+RM5e3av0msTor1LTNzI+PE2qKurYmQ0nFGjjNixI4jHjxOUXptoWyRs27gffjiAn58zX375Gfr6Q5k0yY4dO4K4fv2Q0msTor3LydlBUNA4LC21UVdXRVVVhaVLvbh//7jSaxNti4RtG1VRkcHjxwkkJYXg4WHFp592wMJCmyVLpnD8+HoKC2OVXqMQ7d2VKwfYtWse3t6OGBgMpVu3TsyY4c758+E8e5ZMdbUsoSoaSdi2UU+eJHD+fDi7ds3Dzs6Qjh0/wcXFlL17F3Lu3F6KixOVXqMQ7d39+8fJytrGxo0zsLHR44svOjJhwkiOH1/PrVtHKC1NVXqNom2QsG2jbt+OIiZmDQsXTsLSUptu3Trh7e1AamoohYUxMgpZiDbg+fNUCgqOEROzhjFjLOnUqSP29saEhASQkbFFekyLJhK2bdSFC+F8//0MJkwY2XQ/aOnSKVy+fIDS0lRp5yVEG1BdnUVJSQo5OTvw9XWiV68umJpq4O3lQFjYd9y4cVjpNYq2QcK2jWloaJzHl5GxhRkz3DE318LKSgd7eyN27pRRjkK0RdevH2LBgokMHvw12toDMTHR+GXWwB7pAiQACds2paEhn6qqTEpLUzhyZAVOTiaoq/fHzc2cRYsmk5CwgZKSZKXXKYT4rcLCGHbsCGL0aAvMzDQZNqwfXl4OpKdvpro6S1aUEhK2bUlDQx6lpSncuxfLli2B6OgMQkWlK15eDkRHr+GHHyJkZRoh2qAnT06SmLiRVat8cHBQ0LNnFxwcFMTGruP581Sqq7OUXqNQLgnbNqS+PpeCgmNkZW1j3rzxDBigQq9eXZgzx5NLl/bz4MFxuVcrRBtUVpbGlSuRHD++nilT7OnRozPm5prs2BHEjRuHefq0cfZAfX0uNTXZ0vO2HZKwbUNqa3M4c2Y3O3fOY9y4EaiodOXrr79i9Wpffv4pmYoK6VkrRFtUW5tDSUkyt29HMX/+RFRUuqGnN4TFi78lOTmE27ejgMaOQWVlaVRWZlBXl6P0ukXrkbBtQ6qrs4iPDyYgYAxWVjr069cDbe1B7Nw5T+m1CSHerKoqk5CQmaip9UdXdzBeXg5s3TqH06d3U1eXS1VVJs+fp1JRkUFtrYRteyJh24ZUVmYSFvYd1ta66OoORqFQZ/LkUcTFrVN6bUKIN6uuzuLAgaW4uJhiaamNnZ0hU6e6EBu7lvLydCorM6iqyqK2NluuUrUzErZtRENDHmVlaaxc6UOfPt0YPLgPY8das3HjTE6dClN6fUKIN6utzSYxcSNBQeNwcjJBR2cQFhbabN8+l6dPk6ioSJfm8u2UhG0bUFOTTXFxIlevHmTWLA+6deuEhoYq8+aNJz4+mFu3jii9RiHEm9XW5pCXt5OQkAAmTbJFU3MAOjqDWbt2KnfuHOPp00S5fNxOSdi2AeXl6dy4cZikpBAmTbLj888/xdBwGNu2zeHGjUNNIxmFEG1bXV0uly8f4OjRlcyY4Y66en8GDerDggUTuXhxH/fvx8k0oHZKwrYNePo0kczMrYSGzsLRUUGnTh2xttbl8OEVFBeflLm1Qnwg6uvzKCqK4/Tp3axe7Yu+/lBUVVXw83MmLm4dly8fkPO5nZKwbQOKiuKIjFyKn58zpqYafPXVl7i6mpGYuJGqqkyZIiDEB6KhIY+KinSKi0+yf/9irK11UVVVYcwYSzZsmE56+hZKS1OUXqdofRK2bcCPPx5l/fppWFhooa8/hGHD+jF1qgv5+buUXpsQ4v0kJm7E09MaNbX+jBihx7ff2hMZuZQnT04qvTbR+iRs24DLlw8QEDCaPn26Y2Q0HA8PK0JDZ3Ht2kGl1yaEeD95eTuZP38iI0booac3hOHDv2HVKh+KiuKUXptofRK2b1BXl0t1dfYv8+JyaWjIa7YuHg0NedTX53L69G5Gj7bkb3/7K6amGqxa5UNSUgj37x9X+v4LId7PlSuR7Nw5j8mT7Rgy5Gv+9re/4uPjyK1bR1pkqcYXf0/q6nKorc2htjaburpcWRayjZCwfY3KykwyM7cSHOxPRMQSzpzZw4MH8c3WuP3Jk5NcvLiPHTuCMDfX4r//+284Oio4eHAZP/wQwbNnyUo/BkKI91NYGEty8iZWrvTB0HAYf/3rf+LpaU1m5lYeP06gsjKzWd/v55+S+OGHA6SmhhIdvYZ9+xaTnx8m94jbCAnb1/j5pyRWrfJBVVUFBwcFO3fO4/z58GbrKXvt2iH271+Mn58zw4d/w9///l9MmmRLfv4unj5NpKpKpggI8aEqKUnhxx+PcvjwcuzsDPnrX/8Te/vGD9NXrkQ2+4fp27ejOHRoBYsWTcbLy4FRo4zYvDmQe/dilX4shITtaxUXJzJ3riefftoBff2hBAdPJz8/jAcP3nx5t74+95fLOH/c3ePUqTCWL/fG3t6YYcP60b17J2bPHsuNG4eprMyUHphCfMCqqjL5+ackMjK2MHGiLZ999k+srXVZvtybEyeCmz0Er18/TFjYfKZNc8XRUYGOzmBWrvThzp1jSj8WQsL2td43bBsa8qiuzvqlu8cfh2Zqaig+Pk7o6Q1BS2sgenqDWb9+GkVFcXKvRYgPXON4jywuXdrP3LmeqKqqYGKiwdix1oSEBHDlyoFmfT8J27at3YZtQ0MedXU5VFVlUlycSEFBNLdvR3H7dhR37hyjoCCaCxf24e3tyP/7f//3XmH7orvHv8+Tra1tfN9jx1bj5GTC4MFfY2qqwbhxI9i/f7GsGCXER6SgIJqNG2diba2LqakmRkbDCQgYTVbWNqqrs5ptHv3LYWtvb4y6uipz5niSmbmt6W9bQUE0RUVxPHp0gufPU2UOfytqt2FbW5vD8+ep3LsXy8mT3xMc7M/KlT6sXOnDmjV+BAf7s2KFD2Zmmvzv//79nS8j19XlUF39++4eDQ15lJamUFQUy86djQOjBg7szZgxlgQH+5OevoXnz1OVfnyEEM3j0aMTHDu2mjlzPLG3VzB48NeMHm3BkSMruH//OM+fpzXL+7wIWz8/Z6ysdPnmm17Y2howZ45n09+2deumsWvXd0RFreb8+X3yt6YVtduwrazM5MGDeM6e3cPy5d4oFBpoaw9CR2cwBgbDMDHRQKHQQEWlK3/721/fOWz/SH19LvfvH+f8+XBWrfJBS2sAqqoqBASMJjV1MzdvHpGBUUJ8REpLUzh7di8HDixl/HgbevTojEKhzqZNAfzww34ePz7RLO/zImx9fJxQKNTp1q0T/fr1RF1dFR2dwejoNLbtHD3aklmzPDhyZCUPHsT/Mp1Rblm1tHYbtg8eHCchYQNr1vgxbpwNWloDMTPTYuxYayZMGImjo6JFwramJptz5/ayd+8CvL0dGDasH+rqqqxc6cPNm0d48uSkdAUR4iNSWZlJYWEsp0/vJiBgNCoq3dDWHkhQ0DiOH1/PzZuHm+V9XoStt5cDurqD+fTTDqiqqmBlpYOrqxljx1rj6TkCBwcFFhbazJnjSVTUKi5diqC4WG5dtbR2G7ZXrkSyapUv1ta66OkNYdCgr3FwULBkyRRWrfJh8mS7Fgnbqqos4uODmTVrDDY2egwYoIKh4TB27gyisjKT2tps+ZQpxEekvr5xDMfPPyWxcqUP/fr1YPDgrxk/fiSbNwdy+vTuZnmfF2Hr5eWAunp//vrX/2zqiz179liWLvVqWtGqW7cvMDPTJDDQg8jIpdy40TyBL/5Yuwvb2tocKiszyc7ejo+PE6qqKujrD2XUKCOCgsZz+PAK4uLWERo6i5kz3dHTG8z//M9/N1vYVlRkEB6+CHt7Y/T1h6KlNRBXV3OiolYp/dgIIVpOTU0227fPxchoOFpaAxk1yoi5cz1JTt7ULNtv+mbr7YCe3hA6dvwES0sdVq70ISJiyS8LXSxi8uRR9O/fCyOj4bi7W7B27TTOndur9OPzsWt3YVtRkUFx8UliY9fi5GRC586fY2trwMqVPkRHr+HKlUju3o3hypUDJCeHMG7cCDp0+EezhW15eTobN85EXV0VdfX+2NoaEBQ0jrS0zUo/NkKIllNbm8PRo6uYONEWKysdFAoNxoyx5OjR5vmg/fIAKWtI+J7RAAAgAElEQVRrXfr3V2HaNBeSkzdx69ZRCgqiOX8+nOBgf0aNMsLGRh9raz1mzx5LTs4OpR+fj127C9uSkhQKCo6xb98izMw06dDhH4webdkUtKWlv47O+zOLWvy7urpcKioyKCqKY+HCSfTq1QV1dVV8fJzYs2cBly7tV/qxEUK0nLq6XDIzt7J6tS9jx1qjozMIhUKd7dvnUl6eTk3Nn7uF9CJs/f3dcHU1x9hYjXXrplFQEN30nOLiRI4cWYmfnzMuLqYoFBr4+jqRnr5F6cfnY9fuwvbJk5NcvnyArVtnY2ysxief/ANPT2tOnAjmxo3DvxmG35xhW1aWxs2bR0hKCsHby4Hu3TthZqZJaOgsLlzYx6NHzTMiUQjRNtXX53H9+iHi49czd+44tLQGMnhwHxYv/pbr1w/x6FECNTXZ7739F2E7c+ZoJk2yw9FRwbZtc7h379cuQ0+fJhEdvYaAgDGMHWuNlZUO06e7kZm5VenH52PX7sL2/v3j5OeHsX69P/r6Q/jkk/9jwoSRpKRs4vbtqN80GWjOsH3y5CRpaZvZuHEGjo4KunT5Fy4upvKJUoh2oqEhj5KSZO7ejSY0dBaamqp07foF3l4OJCWFcP36ISoqMt57+y/CNjDQg2nTXPDycmD//sU8eBDf9Jyff0oiLm49QUHjmTTJjlGjDAkM9CA7e7vSj8/Hrt2FbWlpCgUF0U2XkVvrm+29e7Hs378YHx9HRozQY+DA3kyZYk9m5tZfVpGRdZCF+NhVVmbw809JREYuZeRIffr374WrqxmrV/uSnLzpTzUneBG2M2a44+k5gpEj9fn++xncunWUmprGFqEvX0Z2czPH0lJbvtm2knYXti+WaExM3IidnUHTPdtjx1a36D3bmzePsGaNH2ZmmigUGhgbD2f27LFkZW2jrCztT10+EkJ8GBoblOSQlBTCpEl2aGoOwMJCC3d3C3bvnv+nbif9ulyjC6NGGaGm1p8FCyZy8eJ+ysvTqa3N4cmTBPbtW8y4cSOwszPE2FhN7tm2knYXti/k5u5k/HgbunX7AisrHebOHceePQvIydnBxYv7yc7ezpEjK3F1NaNDh/99z64/jUs2VlZmcObMHmbOHI2qqgpmZppMmDCy6X5tRUU6tbUStkK0F6dP72bpUi/s7RUoFOqoq6uyerXvn+oE9CJsfX2dMDHRoEePzowZY0V4+EKys7dz/nw4WVnbWLRoMkZGwzE312LUKCMWLpxEfv4upR+Tj127Ddvz58MJDPRg+PBvGDasH8OG9cPFxZTly30IDvbH398Ne3tjVFVV+K//+tt7NCLIprw8nWfPknn8OIGkpBA8PKz44ouO2NoasGaNHydPfk9hYQy1tTm/WT9ZCPFxu3nzCJGRy5g1awwKhTqdOnUkMNCD27ej3nubL68gpa09iA4d/oG6uiqTJtmxaNFkNm6cydq1U7G3N6ZLl39hZDQcHx8nwsK+48qVSKUfk49duw3bmzePsGVLIKNHW6CpOYB//etThg7th7u7BZ6eIzA2VqNv3x506/YFHTt+grW1Llu2zObs2T08fPj6Sz0NDXlUVTV2/SkqiuPy5QOEhy9kxAhdOnT4X9zdLYiOXsO1a4coLU1R+rEQQrSuR49OcOpUGFu2BGJursV//ud/MHGiLefO7W265Puu27x16ygREUuYOXM0pqYadOnyOQMH9kahUMfRUcGkSXZMnGiLvv5QvvzyM2xtDQgO9ic1NVQazLeCdhu2T58mcvp0GBERSwgM9MDKSgdLSx1GjTLC3l7BqFFG2NoaYGnZOPl8xgx3oqJWcf36IZ4+TXrj9l90/bl27RDHjq1m/vyJKBTqdO78GVOnunDmzB6Ki09K0wEh2qHy8nSKiuI4fnw9jo4K/uM//gN7e2MOHlzG1auR7zVQqqgojsTEjWzeHMiCBROZMsUeDw8rHB0V2Nsb4+CgwMnJBDc3czw8rFi7dippaZu5c+fYb8aqiJbRbsP2hbKyNE6e3MiiRZMZP94Gc3MtzM21GD9+JHPmeDbZvn0uubk7KCqKfaeWWGfO7GbNGj/c3MzR0hpInz7dWbLkWx4+jG+xfRJCfBh++CGCCRNG8pe//AUjo+EsXTqFhIQNFBa++zfN4uJEzp8PJykphMTEEBITN/L99zOYMsUeOztDFAoNzM21mDXLgwMHlnLmzB5KSuTKWmtp92Hb+O3zIPHxwYSHL2LjxpmEhMwkPHwR0dFrmuTk7ODOnWM8e5b8Tt9G09I24+/vipmZJiYmGlhZ6bJ16xzpsiGE4ObNIwQFjaNPn+4YGg7Dzc2c4GB/Ll2KeOdtlZenc+9eLNeuHWqSlraZAweWsHXrHDZsmE5ISADHjq3m7Nk9FBbGUFmZqfRj0F60+7BtaMijvDyd4uJEHj6M5969WO7di+Xhw3iePDnZpKQk5ZeuPO82mCkubh3OziYMH/4NdnaG+Pu7cezYavlEKYTg7t0YQkJmYmWlg77+UIYO7YuXlwOZmdveeVt1dblUVWVRXp7e5NmzZB4+PEFRURyFhTHcuxfLkycnef48laqqTOrrZX5/a2n3YdsSGhryKCtL4/HjBHbt+g5TUw0GDuyNp+cINm2aRVbW9t+sVCWEaJ8ePUrg2LHVBAZ6MGKEHr17d8Pe3pioqFU8e5Ys3zw/IhK2LaCuLpfCwhjy83exdKkXWloDGDSoDzNmuHHiRDBXrx6kqkpOIiHau9LSVM6e3cOBA0uYONGW3r27YWamyZYts7l6NZInT04qvUbRPCRsW0BNTTbnz4cTEbEYX18nhg7th7p6f5Yv9+by5QM8fBj/XkP7hRAfl6qqLO7fj+P8+XCCgsahqtoLA4OhLFo0mcTEjfz441Gl1yiah4RtC6iqyiQpaSMLFkzExcUMTc0BWFpqs337XB4/TqCsLE3ulQghqKvL4fnzVO7fP05wsD/6+kMxMhqOl5cDoaGzOHUqTOk1iuYhYdsCysvTiYhYgpubGSYmGujrD2XMGCuio9fQ0KD8+oQQbUttbQ779y/G3t4YhUKdUaOMmD7djYSEDUqvTTQPCdtmVFeXS2VlBvfvH2f9+mno6AxCW3sgtrYGzJnjSWrqZqXXKIRoe+rrczl+fD1Tp7owcqQB+vpDsLMzJCJiidJrE81DwrYZ1dRk8/RpIleuRDJr1hi6dfuCwYO/Zty4EWzaFMCZM3uUXqMQou2pr88lO3s769ZNxc3NHFXVXgwa1IdNmwKUXptoHhK2zej58zSuXz9EfHwwnp4j+Oc/O6Cm9g1BQeM4fnw9t24dUXqNQoi2p6Ehj+vXDxEXt46ZM91RVVWhR4/OzJ8/kXv3Ynn2LFkGVX7gJGyb0ePHCaSkhLJu3TSsrRubDhgbD2fHjrm/rKksq0YJIX6voSGfZ8+SKSiIZvPmWWhqDqBLl8/59ttRJCRs4OrVSCoqZG7+h0zCthndvRvD3r0LmTLFHn39oXzxRUecnBQkJGyQBvFCiLcSG7sWS0ttunXrhIODgnXrppGaGvpezQlE2yFh24yuXz/EypU+mJhooFCoY2ysxrx54zl9ejfV1VnU1cl0HyHE66Wlbebbb0ehqTkAGxt9Jk60Zf/+JTx69PrWnqJtk7BtRhcu7MPPzxkVla6Ym2vh5+dMePiiP9UQWgjRvpw5s4elS6dgb2+MubkWenpDWLdu2nt1AhJth4RtM6ioyODx4wROnNiAu7sFnTp1xM7OkHXrppKcHCLt9IQQb+369UOEhy/E398NCwttVFS6EhAwhrNnG1viVVdLD+wPkYRtMyguPskPP0Swc+c8LC216dDhH7i5mXHkyAp++CGCkpJkpdcohPgw3L9/nIyMrWzYMB0rKx3+93//zpgxlsTHr6egIJqysrfvpy3aDgnbZnD79jHi44NZvPhbFAp1Onf+DB8fR3JydnD//nEqKzOUXqMQ4sNQUpLCzZtHOHJkJU5OJvz97/+Fra0BO3YEcfr0bh4/TlB6jeLdSdg2g/Pnw9m0KYDJk0dhYqLB0KH9WLrUix9/PEp5eTp1dTI/TgjxdqqrsygpSSEvbyfeXg589tk/sbDQYsGCScTErKGg4JjSaxTvTsK2GaSnbyEgYDQjRuhhYaHNyJGNn0J//ilJ6bUJIT5MP/54lPnzJ9K371coFOp4eo4gJCSAH36IUHpt4t1J2DaDmJi1ODoqUFPrj729MQEBY4iNXUtpaarSaxNCfJju3Ytl8+ZAbGz0USjU0dQcgK+vE1lZ25Rem3h3ErbNIDx8ERoaqnTv/iVjxliyc2cQ+fm7qKiQe7VCiPfz+HECUVGrmTXLA4VCnY4dP8HMTJPY2HVKr028Ownb91Rfn8uTJye5ceMwq1f7MnRoX/r168Hs2R5kZ2/nzp1jsmKUEOK9Nd633cXu3fNxcTHl888/RU9vCGFh3/Hw4QkZlfyBkbB9TzU12Vy5EklMzBr8/V0ZMEAFNbX+bNoUwM8/JVFRkUFDQ57S6xRCfJiqqjK5ezea06fDmDrVmS5dPkddXZXVq/04dy6cBw9k/v6HRML2PVVWZpKaGsqKFT6MHm2Bmlp/LC21iYxcqvTahBAfvtraHEpKUigqimPp0in0798LdXVVZsxw5/DhFVy+fEDpNYq3J2H7nsrK0oiIWIK7uzkWFtooFOpMmmRLfPx6pdcmhPjw1dfnUV2dRVlZGlu2zMbYWA0dnUG4uJiycOEk0tI209Cg/DrF25GwfUcNDXnU1eVQXHyS4GB/NDQGoKs7GEdHBYsWTZaRgkKIZtXQkMfhwysYM8YKhaKxyYm7uwUHDy6jtjaH+vpcCd0PgITtO6qpyebnn5K4ejWS+fMn0L9/L4yMhjN9uhvh4QtlDpwQolk1NOSTmhrKwoWTcHExRVd3MAqFGqGhsyguPvnLwjnSUaytk7B9R+Xl6RQUHCMjYwu+vo5069YJU1MNgoP9ycnZQVFRnNJrFEJ8XC5e3Mf+/Yvx83NCTe0b+vfvxaJFk/nxx6MUFyfKzIcPgITtOyouTiQnZzvbt8/F3d2C7t2/xN7emAMHlnL7dpQ0eBZCNLuiojhOnQpj9Wpf9PWHoKLSFW8vB44fX8/lywcoL09Xeo3i9SRs39G9e7EcPLiMmTNHY2mpQ8+eXfD0HEFa2mYqKjKorZV1kIUQzauqKpNnz5KJjFyGpaV204f81at9SUoKkaVhPwAStu/oxo3DrF/vj62tAcbGaqip9WfWrDGcPx+u9NqEEB+35ORNeHhYoaqqgpmZJuPG2RAevkjm3H4AJGzf0cWL+5g5czQDB/bGyEgNR0cFGzZM5/r1Q0qvTQjxccvP38W8eeMxN9fCyGg42toDWb3aj4KCaKXXJl5PwvYt1dXlUFmZSWbmVsaMseTzz/+JiYkGc+Z4cuTISgoLY5VeoxDi43blSiTbts1h8mQ7DAyG0rnz58ycOZorVyKpqcmmvv7No5IbGvKor8+TFe5amYTtWyouTuTy5QPs3j2fkSP1+eKLjri4mBEW9h35+bsoLk5Ueo1CiI9bYWEMCQkbWLHCBwsLLTp0+Afjxo0gKSmE+/ePv3GgVENDHjU12VRWZlBTky2B24okbN/Sjz8eJTZ2LfPnT8TQcBidO3+Gr68jubk7uH//OJWV0uFHCNGynj1L5tq1gxw6tAx7eyP+8pe/YGOjz+7d87lwYd8bP/TX1+dSWZnBs2fJVFRkyPzcViRh+5bOnt3L99/PYMKEkRgZDWfQoD7Mnz+BH36I4OnTRKqrs5ReoxDi41ZRkcGjRydIS9vM+PE2/N///Q8KhToLFkwiJmYtd+4ce+3rX3yzLS9Pp7o6i/p6+WbbWiRs31Jqaij+/m5N6yCbm2sRHOzPrVtHKC1NpbZWJpULIVpWXV0uVVVZXL58gOnT3ejUqSPa2gPx8LAiJGTmW61gV1+fR11d7i/3bZW/T+2FhO1rNDT8uhD4oUPLcXRUoKGhiq2tAT4+jkRGLuXBg8ZLyHI5RgjRWgoLY1izxg8trYHo6Q3B2FiNgIDR5OTsUHpt4tUkbF+jvj6Xn39K4s6dY2zcOBNd3cEMGKDChAkj2bZtLtnZ2yktTaG2NkcGGgghWs3jxwkcPryCqVOdsbLSoV+/nri4mJKYuFHptYlXk7B9jdraHAoKosnN3UFQ0Dj69+9J3749mD17LDk5O7hz55isSSqEaHXPn6dy6lQYe/cuwM3NnE6dOmJoOIyDB5dRWZnZtJJdQ0NeE2XX3N5J2L5GVVUmp0/vJizsOyZPtkNVVQV1dVWCg/0pKIjm55+S5PKxEKLVVVZmcvt2FDk525k2zZWePbugrT2QdeumcfHiPh4+jKehoXF9gKqqTKqrs+RvlZJJ2L5GeXk68fHBzJkzFjs7Q1RVVTA11SAiYgl1dTkykk8IoRR1dbk8f57G48cJrFjhjapqL4YP/4bp0904fHgFly8faBpzUlqaSllZmlyFUzIJ29d4/jyV8PCFuLiYYmamiZHRcCZOtOXEiWCl1yaEaL9eBGl5eTrbt8/F1FQDbe1BODkpmDdvPMnJm6ivz6O2NofKygyqqjLlm62SSdi+xrNnyXz//Qy0tAZiYDAMV1czli71IjdXRvwJIZSrcQpPDkePrmLChJEoFOpoaw/CxkaP8PBF1Nfn0tDwYppPrty3VTIJ21eorc3h+fNUbt06wvz5E+nb9ysMDYcxfbob4eGLuHz5gNJrFEIIyCczcysrVnjj6mrGsGH9GD78G9atm8bTp4lUVGS81XrJouVJ2L5CWVkaN28eITFxI15eDnz11ZeYmWmyZo0faWmbKSyMUXqNQggB+Vy7dpDo6DXMmeOJjs4g+vfvRVDQOC5c2EdRURxVVbK6XVsgYfsKT56cJDNzK6Ghs3ByMqFLl39hZ2fIvn2LuHHjsDRqFkK0GU+enOTq1YNs2RKIQqGBikpXpkyxJzp6DZcu7aesLE3pNQoJ21e6c+cYe/YswNvLAUtLbb75pheTJtmRmPg9T56cpKJCmg4IIdqG8vJ0Hj9O4ODBZYwcqY+KSlccHBQsX+7NyZPfS0eyNkLC9hUuXz7A4sXfYmg4HF3dIWhqDmDuXE/Onw+XgQZCiDblxSCoxMSNuLqaoaLSDSOj4Xh4WLF793zu3z+u9BqFhO0rnTu3Fz8/Z/r164mh4XBcXEwJCQng5s0jSq9NCCFeJT9/F7Nnj8XYeDi6uoPR0FBlxQqfN3YCEq1DwvYV8vJ2MmaMJZ999k/MzDSZN288x46tpqgoTum1CSHEq1y7dpBt2+YwaZIt2tqD6Njx/zF1qgvXrh1Sem1CwvY3ysvTefgwnqioVdjY6NGhwz9wcFAQFvYd+fm7ePpU7n0IIVpHQ0NjM5TG1erePH3n/v04UlI2sWaNHwqFOn/5y19wdzcnI2Mrz54lS89tJZOwfcmdO8dITNzIkiVT0Ncfyr/+9SlTptiTnr6FgoJoysvTlV6jEKJ9qK//dZWo6uqsN44VKStL4+7dGE6cCMbFxZT/+I+/YGWlw65d8zh/PpwnT04qfZ/aMwnbl5w+vZv16/0ZM8YKdfX+qKh0Zf78Cdy+HUV5eTp1dTlKr1EI0T7U1+dSUZHBs2fJVFb+fnGKP+roc+vWUfz8nPif//lv9PWHEhQ0jmPHVnP7dpTS96k9k7B9SVJSCH5+zpiba2FiosHIkfps2zaHR49OUFOTLY0HhBCtpqEhj5qa7F9a5mX/JlR/fSyDmprfPnb3bgxLl3oxcGBvTEw0GDvWmg0bpnPx4j6l71N7JmH7ksOHVzBypD7DhvXDwUFBUNA44uODKStLk+k+QohW90ffXuvrc6msbPzW++9LMj58GM+OHUE4OCiwttZFodBg+nQ3srK2K31/2rN2H7b19Xk8f57Go0cnCA2dha7uYAYMUGHSJDt27pzHqVNhVFVlKr1OIUT7VV+fS01NNrW1ja09X+76U12d9Zurbk+fJhIdvYbAQA/s7Y0ZOrQvrq7mxMaupbw8XVrtKUm7D9va2hzu3Yvj7Nm9LFgwEVVVFfr370VgoAepqaHcunVUfjmFEEpVU5NNWVkaFRUZ1NY2jh15eaRyQ8Ovzy0tTSU7ezvbts1h9GhLevbsgkKhxu7d83n4MF6Wb1SSdh+2VVVZXLy4n8OHV+Dl5UCfPt0ZPLgPK1f6cOPGIZ48OSl9IIUQSvUuYVtZmcH164dJSdmEr68TPXp0Rl29P8uWeZGXt5PCwli5LaYE7T5sy8vTSUoKYenSKTg4KOjbtwf6+kPYvn0uP/+UREVFhvxiCiGU6l0uI9fW5vDzT0ncvRvNihU+DB78NUOGfM2ECSMJDZ1Ffv4uabunBO0+bEtLU4mIWMLYsdYYG6sxcGBv7OwMOXp0ldJrE0J8/H4dBPX2r3l5WtDretbu3j0fY2M1Bg/+GlNTDby8HIiOXiPTGJWg3Yftzz8ls2lTAIaGwzAyGo6dnSFBQePIzNyq9NqEEB+3103vebvX/X7qz8tiYtYycaItJiYaGBgMY9QoI/btW9R0KVq0nnYftsXFJ1m8+Ft69eqCgcFQZs4czYEDS7h69aDSaxNCfNzetHDF6/zRtKCXZWVtY8UKH9zdLdDUHIC29iC2bAmUsFWCdhu2lZWZPHx4glOnwpg61ZkuXT7H0lKH0NBZnD69m4cP45VeoxDi4/auSzLW1+dRW5vzyyI7bw7mK1ciOXRoOQEBo9HSGoiqqgpLlkzh3r1YSktTJHRbUbsN26dPEzl9ejd79y7Ezc2cTp064uJiRkLCBp4+TaKyUubWCiFa1otmA40Dn94cnrW1OVRUZFBWlvZWUxIfPozn/PlwgoP90dUdTLduX+Dn50xOzg7u3DlGZWWG0o9Be9Fuw7awMIajR1cyd64n1ta69OjRmSlT7DlzZo/SaxNCtA+/7ezz5vu17xq2ZWVpPHx4goiIJVhYaNGtWydGj7Zk9+755OXtoqQkRenHoL1ot2F79epB1q6dip2dIQqFGmpq/Zk715NLl/YrvTYhRPvwZy4jv838/5qabMrL00lI+J6xY60ZOLA3I0ca4O/vyqFDy+V2WStqd2Hb0JBHXV0u+flh+Pk5o6qqgq7uYGxs9Fi3bhrXr0ujZSFE6/gzA6Re9qaBUqdOhREY6IGh4XAUCnVMTTVYv34at29HvfO0I/F+2l3YPn+eRlFRHFFRq3BxMaV7905YWekwe/ZYjhxZyb17sUqvUQjRPrztFJ7XqavLoaoq65fFLV4d1leuRBISEoCn5wjMzDQZMECF2bM9OHt2z1tfkhZ/TrsL24cPT3D27F5CQmZibKzGP//ZARcXU/bvX8zZs3v5+adkpdcohGg/3mYKz+tUV2fx/HkqZWVpfzi6+O7daGJi1rJw4SQsLbX5/PN/Mn68DcnJITx8GE9FhQyUamntLmxv3jxCTMxagoLGoaMziE6dOuLt7UhW1nYKC2Pll04IoVTvOr2ntjabiooMKisz/3BlqKdPE7lwIZz9+xfj4mLKP//ZATs7Q3buDOLMmT08fpyg9P3+2LW7sD17di+hobOYONEWTc0B9OnTnYULJ1FQEE1FRYY0HRBCKNWLEcdv2w6vvj6Puroc6upy//DbcXV1Fs+eJXP6dBje3g58+mkHDA2HM2eOJ0eOrOTWraNK3++PXbsL27S0zQQGemBjo4eu7mD09IawaVOADIEXQrQJjWGb/tb3Ul8M+mzs/vP6S9F378awYMEkVFS6oKMzCDc3c9atm8a5c3uVvt8fu3YXtlFRq3F2NkFDQxVzcy3GjbPh4MFl0uNRCNEmNF5Gzn7r6T21tTlUVmZQVZX5xuc/eBDP5s2BWFhoo1CoY2g4DD8/Z9LTtyh9vz927SZs6+oaW1Tt2jUPbe2BfP31Vzg5mbBqlS9paZtlxSghRJv2R1N0qquzKC1N+WWA1Ou/CT99mkhU1Cr8/d2wttalX78e2NsbEROz9rWXocWf1y7CtrY2h/v3j3Px4j6WLJnC0KH9GDq0L3PnepKSEsqtW0ff+EsqhBDK8mJ6z6sGTdXW5lBVlfnaqT8vlJWlcepUGHv2LGD8eBv69OmGsbEa27bNpbAwlpKSFAncFtIuwrayMpPz58OJjFyKl5cD/fv3Ql9/CGFh31FWlvZWK7cIIYSyvJjeU16e/rvpPe8ydaimJpsHD45z6dJ+5szxpFevLgwd2pfFi78lP38XhYWxb7VspHh37SJsy8rSSE4OYflybxwdFfTt+xU6OoNYu3YqFy/uF0KINu3s2T3k5e3i1Kkwzp0Lf+/tnD8fTk7ODpKTQ/Dzc6Jnz858801PvLwc2L9/MRcu7JMZGS2kXYRtSUkKBw8uY/JkOxQKNb7+ujtqav3x9nZg69Y5QgjRpm3eHEho6CxCQ2exZcvs997Oli2z2bQpgA0bZuDiYspXX32JikpXbG0NWLhwEsnJm6TtXgtpF2H77Fky+/cvZuxYK4yN1VBVVWHo0L7Y2Rni7eWAj48jvr5O+Pk5M3WqC1OnuuDn54yvr1Ob9KLOadPadp2/elGva5s/tn98rBtr9/X9cGr/o+P/Ye7D738mH9rv0tvs17RprbdfFhbaqKh0RVW1FzY2+syZ48nJk99L2LaQdhG2z5+nEhe3jtmzx+LsbIKOzmDU1PpjYDAMS0ttbGz0GTXKCEdHBa6u5ri6muPoqMDe3rhNaqzTDDc3c5ycTJRez5spcHY2xd3dAhcXU+zt2+6x/XcODgpcXBprd3Y2VXo9f+b4jx79Yh8+nOP/Ko6OCtzczHH9/+3dV1SWV9738ZNnrWetWe/MpD1OrKNhrIgNREQ60m4VFEEBe0cNTcUuYhdQRKoIgmBDAaUjvXeNJk5sEUFFRdFEmnS+7wFCTMQkxihtH3wOslbui31dyPW7d/vvBdM69d/pu5o7d0rbfZmZffj70tVVYsKEUejpKWFtbYav7zYKCgLFMPIH0vico4YAACAASURBVCPCtro6g5wcf7y9N7N+/QJMTHTR1lZEVVUOJaVxaGjIo6urhL6+GkZGWhgZaaGvr4aennKnNG2aKkZGkzE27tztbCWRqDBjhgazZ+swY4YGU6aodHib/qgpU1QwNNRk9mxtpk9XRyLpOm3/9fM3Mel6z789XeXv9F0ZGKgza5Y2M2dOZupU1bf8f0q/8v4/d8mSGbi4rCU+3oMffrjwp08eEn5bjwjb+vociooiyM72IzLyEAEBO/D03Iirqy0uLmtxd1+Pl9cmfHy24u+/HX//7fj4bOXIkc2dko/PVvz87Dp9O1t5e2/m2LFtHD9uz7Fjdnh7b+nwNv1RR49u4dgxO44ft2+b7+roNr3789/y2vPf1qWef3u6yt/pu/L13Ya//3b8/Ow4erT935Gn50bc3GxxdV2Hh8eGv+TnBgXtJS3tKDdvhlJWliB2ZnwgPSJsm5tbDmiuqkrnxYsUysoSefIkgSdP4iktjefJk3iePk3g6dMEysoSKStLbPvvzqqrtPPX7e1Kbe4Obe9O99De/XR0Oz72fT16FEtxcSSFheGUlMT8JT/z+fMkKivTqK3NEvO1H1CPCFtBEITuoLExl5qaLKqrM6ipyWor6Sh6o52fCFtBEIQuovXQgfr6lmP1WnukohBF59dpwra+Pofy8lRKS+O5fz+aO3fCKC2No6Ym8w+dZiEIgtBVNDfn09T0x07qaU9TUx61tVlUVKRSU5PVIYuaamoyefw4jjt3wigsDOfu3QgKC8O5cyeMH35ocedOGHfvRnDvXhRPnya8qoD1x87p7W46Tdg+f57ElSuniY524fhxe5ycbIiKcuH+/ahXp1mIuQRBELqHxsaWsKypyfxT86TNzS0HzNfVZdPQkNshnZF796IICzuIk5M1hw6twc2tZcHpgQM2ODpa4ehohZOTDe7u6/H13da22vnFixRqa7M7/HfwsXWasC0ujuTCBSd27jRn0SID1NXl2bHDnEuXTlBenkJdXc/75QhdR2tt2qamPBobc2loyG070Lu19yJGZ4RW9fU5VFWlU1GR2mXfbd98c4qtW5eiri6Pnp4SBgZqTJmigra2IpqaCmhqKqCtrciMGRrMmSPB0dGKlJQjFBdH9sjzwztN2P73v2dxdrZh1ixtVFRkGT5cikWLDDh1ajfffnuGsrKEDn9YgtCe5uZ8qqvTefo0gTt3LnDp0gmys/24dOkE164FUVQUwbNnSe0WkRd6psbGPOrqsrv0CuDc3OOsWjULaen/oKw8Dn19VYyNtTAzkzB37lTmzp2KmZkEAwN1tLQmYmqqx5o1c/H23szlyye79L3/GZ0mbHNz/bG0NGXkyMEMGNCHTz75J5qaE9i+fTkREc7cvRve4Q9LENrT1JTH06cJ3LwZQmKiJ35+dri62uLnZ0dw8H4yMny5c+cCZWUJ1NaKc5OFApqbW+dtu+6IR1raUUxN9ejV63PGjh3OtGkqLFgwDWsrMzZsWMiGDQuxtjJDX1+N0aOHIi39H6Sl/4OxsRbnzu2noiKV2tqsLnv/76rDw7amJovnz5OJjDyEqaku/fr1ZuDAvkhJDUBVVZb586dy6NAarlw51eEPSxBe9/JlJvfvR3H58knCwg7i5mbLjh3mrFkzFwsLE2xs5rBhw0IcHa04dmwbSUlePHgQTUNDbo9cICJ0Lykp3hgba/Hpp/9EVlaaWbO0Wb9+AV5emzh9eg+nT+/B3387mzcvYfZsHRQVxzBgQF9UVGTx9t7Mo0cXqahI6zErqTs8bMvKErl+PQQfn63o6k6iV68vGDVqKDo6ikyerICamhwWFiakpHh3+MMShNc9fZpAYqInhw6tYcUKI9TVx6OmNh6JRAV9fTV0dSehqTkBiUSJ6dPV2b17FXl5x6muzqC+PqfD2y8I76M1bD/77BMmThzN4sUGuLmtJzvbj8LCcAoLw7lxI4TYWDe8vTezYME0hgwZyIQJMjg723D7dkvFqp7yxbPDw7awMIy4OHd27lyJqqoc/fv3Rlt7ItbWZhgaajJq1FBmzNAgNNRRvKSETuXevSiOH7dn6dIZ6OhMQlr6PygojGLGDA3MzCTo66uhoTEBWVlpBg8eyJw5Es6fd+LRo1gqK9M7vP2C8D5aw/bzzz9BSWkcK1YY4e+/nVu3zlNVlU5VVTrPnyfz7bdniIpywcrKjGHDvkJWVhpHRytu3AjmyZP4HnPwQYeHbV5eAIcPr2P5ckM0NSegoDAaS0tTTp/eg4WFCSNHDkZDQx5Pz43cuRPGs2dJPWaMX+jcCgvDcXOzxdhYi0WLDLCyMmPv3q8JCNhBaKgjJ07sxMNjA/PmTWH4cCmmTVPFzc2WvLwAHj6M7fD2C8L7eL1nq6AwmkWL9Dl8eB3p6T7cvBnKzZuhfPvtGSIinHF1tcXUVIKUVH/k5WVwc7PlwYNoystTxTDyxxIT48rq1bOYMkUFHZ1JGBlp4em5kdu3z7Nv39eMHDkYWVlptm9fQXq6D0VFET3mm5DQud2+fR4HByskEmW2bFlKWNhBrl49Q1lZIjU1Wbx4kUJxcSS7dq1EWloKVVU5Nm9ezIULB7h5M7TD2y8I7+P1OVs5OWlMTfWwt19BUNBe4uPdiY93JyLiEIcPr8Pa2gxtbUX69++NouIYjh3bRnl5CjU1YoHUR3P27D6mT1dHRUUWExNdNm5cRHj4QUpL4/Hy2oSysizy8jIsXz4TL69N5OYep6FBDCULHe/Ro4tcuHAAe3tzDhywwctrE35+2zl5chcBATtwd9/Arl2r0NdXo1+/L1FVlWPXrpUkJHiI1fVCl9catn//+/9j0KB+jB8/EolEmfnzp2Fuboy5uTHLlhkyc6Ym6uryyMlJM2zYVxgYqHHu3P62gh7NzR1/Lx9Dh4etj89W5OVlGDt2OObmRvj52VFQEEhtbRZnzuzFwECdiRPHMG2aKpaWpkREOHfZTeBC91JRkcb3358jLs4dX9+t2Nktx8LClAULpmFgoI6ysiwyMoPp378P//jH31FVlcPJyZrsbD8ePIju8PYLwvtoDdv/+Z//4R//+Duff/4p//rX/9G375f079+H/v370K9fb3r37kWvXp8jJTUAWVlpli415OJFty697enP6JCwbWjIpawskcLCMHbtWsWIEVIMGTIIU1M9HBwsCQraS3a2H46OVujqTmLs2OHIy8swdaoKPj5bef48ibq67B4z1i90Tq2rkQ8fXsuWLUtYtsyQBQumMW/eVExN9TA01ERPbxIyMkP44otP0dCQ59ChNeTlBVBSIuZsha6tNWz/9re/0bt3LwYPHoi8vAw6OooYGKhhYKDGtGmqaGtPRFlZFgWFUW1bhAIDd4o524+hujqDb789w/nzjqxYMRMpqf70798bVVU55s2bioWFCVu3LsXMTIK8vAyDBw9k4MC+jB49lN27V3H3bjjl5SliOFnoUC1ztpZMnqyAnp4SU6e2bOrfsGEhDg6WuLra4uGxAVNTPQYO7IuOjiIuLmtF2ArdQmvYfvLJPxg9eigGBmps2rSY06f3EB/vQXy8BzExhwkM3IGzsw3z509FRmYIiopjsLNbRlKSF3fuXOgx7/EOCduffkwmJsaV7duXM326OlJSA5CS6o+qqhyzZmkzZ46ERYv0MTTURENDntGjh9G3778YMKAP1tZm5OUd58GDaGpqMjv8AQo9T2upvby8AJYvN+Rf//o/xo0bgb6+GtbWc/Dy2kR4+EHi4loWiVhamjJ48L/R1Z3E4cPrRNgK3cLPW38+RVlZllWrZnHq1G7u3/95iqS+Pof796MpKDiBvf0Kxo0bgYzMEMzNjQgI2MHlyyd6zLRgh4RtaWk8vr7bMDTURFVVjjFjhqGuLs/q1bNxdLTm4EEbXFzWsn+/Jfb2K1i4UJ9x40YwcGBfFi82IChoL5cvn+TFi5QOf4BCz1NdnUFpaRyxsa6YmUn44ovP0NFRZNu2ZZw4sZPMzGNcunSC6GgXvL03Y2qqR79+vdHUnCCGkYVu44+EbVNTHuXlqTx8GMuRI5vR1p6IgsJoli0zxMNjA9nZfj2mhOlHD9vm5gLu349m586VDB8uxdixw1FWlmXx4ul4eW0iJcX7DW5u65FIlJGS6o+R0WT27bPg4kU3njyJ7/AHKPQ8P/2YzO3b5zlzZg/Tp6vz2WefYGoq4ezZfVy9epqyskQePIjm/HknNm5chLb2RHr1+hxVVTkOHrQhN/c4JSUxHX4fgvA+fh22K1cac/LkLu7di2o7q7dVY2Me5887YWKii6bmBJYunYGDgxWpqd7U1Iiw/cvV1WXz4kUKV66cwtZ2AVJS/VFTG8+KFUa4uKwjIcGT27cvvOH8eSeWLp2BnJw0urqTmDtXgo/PVoqLIzv8AQo9z8uXmTx5Ek9Skhfm5kYMHvxvNDUnsGTJdGxtF7Bnz2p2716NtZUZpqYSlJVl+eqr/kyerICdXcvBGrdune/w+xCE9/Hr2sizZ+uwc+dKwsMPkpXlR1aWH5mZvsTHexAe7szGjYuYNGksEyeOZtWqWfj6biM/P6DHnG37UcO2qiqde/ciSUz0ZOVKY/r1+5IZMzRwc1tPaupRiooiqKnJfEN+fgB2dsvR1p6IktI4xo0bwbZty7h5M6TDH6DQ8zQ15VFfn8O1a0Fs374CBYXRyMgM4auv+jFoUD/+859/M2KEFLKy0igpjWP8+JGMHj0UPT0lrKzM8PHZyjffiIM1hK6tNWz/+c+/M3y4FJMnK7B48XTs7c1xdl6Ds/ManJys2bRpEebmRkyerMC//92y0NXa2owLFw7w3/+e7TEleD9q2D57lsSVK6cICtrLihUzkZaWYuVKYyIjD1FYGPbWA4Vv3z7PsWPbWLnSGH19VWRlpdm4cRGXLp2gqiq9x/yyhM6lpCSGc+f2s27dfBYsmIaenhKTJyswebICU6aoMHfuFCwsTNrY2S3H03MjUVEu3L4terZC15aR4cu8eVPp3bsXI0ZIMWnSWPT11Vi8eDoWFqZYWZlhYWHKvHlTmDZNFTW18cjJSWNgoIaLy1ry8wPbTsHq6Hv5GD5q2D58GEtioifu7rasWmWMhoY8u3at4sqVU1RUpL01NB89ukhy8hE8PDZgaWmKru4ktm1bSkrKEUpKYkRRd6FDVFdnUFgYTm7ucWJiXDl1ajcBAfYEBNgTFLSX2FjXtuG0rKyWw+S//z6Ye/ei3vrFUhC6itzc46xePYvhw6UYPXoY8vIyqKvLM3WqCkZGWpia6mFmJmH6dA10dBQxNNRk0SJ9du9eRWKiJ0+fJlBVld5jClt0SNgeObKJHTvMWb26ZfXa7xVlLy9P5dat868FrglubrakpbUMPYsXl9CRmpvzqahI49GjWB48iObBg2hKS+OoqhJfAn9+RgU0NeXT1JTXY16u3d21a0Hs32/B9OnqbYyNtTEzk7BggT7LlhmycqUxS5ZMZ968qdjazsfVdR3R0S4UFva8cqUfNWwrKtIoLAynoCCQ1FRvoqJc+O67M1RWpv3m52prs3n2LJG7d8PJzw8gJuYweXnHKS6O5MWLlB4zwS50Ts3N+dTVZVNZmUZ5eSrl5alieuNXmppa9ia31MMVz6U7KC2NJyPDt+2g+NOn93D27D5CQhy4cOEA4eHOREYeIizsIKGhTsTHu5Obe5xbt87z04/JHd7+j63DayMLgtD9NTTkUlWV3uNOehGEViJsBUH44H7Zs+0ZC2I+ltaKZvX1OTQ1ieNHOysRtoIgfHDNzS3D7WLO9q/XOoVRXZ0hvsh0YiJsBUEQurD6+hyqqzOors6gtjabhoZc0cPthETYCoIgdGFNTXk0NORSV5fNy5ctoSsW53U+ImwFQRC6gYaGXKqrM6isTKO2NksM2XcyImwFQRC6gdYyorW1WdTUZPLyZSb19TkicDsJEbaCIAjdSFNTHi9fZvLTj8m8fJlBY6OYv+0MRNgKgiB0I83N+dTX5/DyZctBLrW1WWJbUCcgwlYQBKGbad1mVVubJbYFdRIibAVBELopsS2o8xBhKwiC0E2JbUGdhwjbHq6qKp3Hj+MoK0tsq1nb0JBLbW02VVXp/PRj8m8efygIQuf3+ragujpxcMuH0DJ036K9FeAibHu4q1dPExCwg/DwgxQVRdDQkMuLFyk8eBDN1aunSUryIj8/kCdP4ju8rYIg/Dmt24Lq6rJpbBRztx9CY2MetbXZ1NRktTs/LsK2B2tuzickxJG5c6ewfv1CcnL8qa3N5sGDaK5cOUVoqCMHDthw4sRObt4M7fD2CoIgdFb19TlUVqZTUZHa7rGvImx7sObmfIKDHTAzk2Bru4Ds7J/D9ptvThIS4oCjozUBATtE2AqC8MG09ry78hallp5tlujZCm8SYSsIQmdQX59DVVU6VVXpXXZ9yM9ztu2XyRRh24O1H7ZZFBdHkp8fwLlz+3F0tBJh+w6qqtJ58CCG4uLIV4vOukfJvNraLF68SOHp0wQePbrI48cXqaxMa3vBNDTk0tiY2+XvU+gYDQ25vHzZUmKyu+4HFmHbg7UXtjU1mdy5E0ZGhi+nT+9h/35LEbbv4N69KOLjPQgPP8jlyycpLY2nsjKtyw6NtXr2LIlbt0IpKDhBeroPGRk+FBVFvNpa8nO1ou76ohQ+rNYvbC37gLvnFzYRtj1Ye2H78mUmP/xwgdTUo5w8uUuE7Tu6cuUUhw+vY8eOlYSFHeCHHy5QVpbwuyH0e9sGOtq9e1Gkp/sQEuLIsWPb8POz49KlEzQ2tuzhrKpKf1WlqGsOAQrChybCtgdrv2ebRVFRBDk5/gQF7cXBQQwjv4ukJC9WrjTG2FgLV1dbvvnmFA8exPzuPFTrtoHa2vYXV3S069eDCQ524OBBGzZuXMTmzUuIj/egvj6HxsY86uqyu/TiFkH40ETY9mBvm7MVC6T+vOBgBzQ05BkxQgpb2/mkpR3lzp2wdrcCvO71bQOdsehAQUEgHh4bsLYyY9YsbUxMdDlzZm+nbKsgdEYibLugmppMysoSuXs3gqtXT5OR4Ut2th95ece5fPkk166dpbAwjJ9+TP7N6/xWzzY315+goH2/27Otr8+hvDyVR48ucvNmKPn5geTlBZCXF8CNGyG/24bu5ty5/aipyTFs2FesXTuPlBRvrl49TXFxJCUlMZSUxFBaGk91dcYvPvd72wY+ppcvM3n8OI67d8O5dy+KkpIYLl50w9HRipUrZ2FoqMmsWTqcPr1HhK0g/EEibLug58+TuX49hOTkIwQE7GDv3q85cMCGw4fX4eOzlTNn9hAf70FhYdhvXue35mzT0o5y6tTu352zrapK5/79KL755iTh4Qfx8NiAm9t63NzWc+HCgd9tQ3fz67BNTj5CRoYvOTn+5OYeJzf3ON99F/RGRa7WU1retm3gY3r2LIkrV1qqh6Wn+5Cbe5xTp3azffsKli41ZPp0DRG2gvCORNh2Ec3N+VRWttQxzss7zokTO9m714LNmxdjZWWGjc1cbG3nY2u7gHXr5rN79yrCww9y504YZWWJ7c4Zvi1sb98+T3LyEU6c2PnWsC0vT+XevSjy8gIICXHAzc2WPXtWs379QqytzDA3N2bbtmWcOrWbvLzjFBdHvioV1/Fh8iG1hu3AgX2ZNUubAwdsOHRoDW5uthw+vI6DB23w8tpEVJQL3357hocPY393Pre6OoOHD2O5cSOEgoJAkpOPkJjoRUKCB/Hxb5eXd5yioghevEihtjbrrf+u6utzqKnJbJurDws7wJEjm3FwsMLZeQ1ubuvZunUpS5fOwMhICz09ZRG2gvCORNh2EU1N+RQXR5KR4Yubmy3z5k1BS2siZmYSrKzM+PprE1atmoWpqR4aGvJoaU3E1nY+Z87s4dKlE1RWpr9xzfcJ21u3zhMV5YKjoxULFkxDR0eR2bN1MDc3wsREF21tRfT0lDA11WXt2nmEhzvz04/J1NZmd+tFNK1h+/nnnzJ8uBQqKrLo6ChiYKDOlCkqaGhMQCJRxtzciP37LUlM9KS8PPU3r/ngQQxJSV54e29h48ZFmJrqYWyszYwZGkyfrv5Wa9fOIyTEkZs3QykrS2z32o2NeVRWplFaGkdIiEPbnOyMGRpMm6aKgYE6M2ZooKs7CRUVWZSVx6GqKifCVhDekQjbLqKxMY/vvgvi7Nl92NjMQUFhFEOGDGLmzMls376cTZsWsXbtXAwNNRk27Cv69++DRKLMxo2LiIhw5tmzpDeu+T5bfzIzfdm3zwITE13Gjh3OoEH90NFRxMrKjDlzJGhpTUReXoZRo4aipDQOZ2cb7t+PpqIitW1OsnW7S3fq6baG7f/+7//yySf/oFevLxg6dBAKCqOQlZVm6NBBDB06iAkTRjF1qgqenhu5fz/qN1fy3r59gbNn97Fp02IMDNQZNuwrpKQGMGBAH/r16/2G/v37MGBAHyQSFVxdbbl06QQPH8a2e+26umxKSmK4evUU9vYrkJUdwVdf9WPs2OEoKY1rIys7gmHDpJCWHoyCwmgRtoLwjkTYdhGvh+3OnSuZN28KpqYSDhywISnJi7g4d2JiXNm792u0tRUZPlwKTc0JzJ8/jcDAnZSWvnlqz/ts/QkLO8DChfpoaU1EW1sRY2Mtdu1aSWTkIc6d28+xY3Zs27YMQ0NNtLQm4uBgyZUrp3j4MJba2iyamlq2i3SGBUF/pdd7tiNGSKGhMQFzcyMOHVqDs/MaduwwZ/XqWejqTmLUqCFs2LCQrCw/Hj26yMuXme1e8/HjuLbfh5OTddtIxsqVxpibv+nrr2djbWWGs7MNCQke3L0b/taFauXlqWRlHcPbezNLlsxgzJhhKCvLYmMzhyNHNrcxNzdiwgQZEbaC8CeJsO0iXg9bNzdbdu9exaFDa8nO9m+rvNLQkEtioifLlhkiJyeNktI4tLQm4ua2vt2ezfts/fH13cakSWMZN24Ec+ZIcHS0Ji3tKLW1WW1HeeXk+LNhwyL09dXYvXs1CQme3LwZSlVVOg0NuVRVpVNenkptbVa36d22hm3fvv9i8mQFrK3nEBLiyJMn8fz0YzLFxZFERDhjaqrLJ5/8A1NTPc6e3ce1a2ffGohVVek8fBjD9evB5OT4Exfn/ptSUrzJzvbj2rUg7t+P/s052ydP4jlzZg9Ll85AV3cSMjJDMDWVEB19mLq67Db+/tvR1p4owlYQ/iQRtl1EU1M+JSUxFBQEEhy8n337LNi0aTGHDq3l5Mld+PnZ4e29mTVr5qKmJsfQoYOQk5NGU1MBV1dbSkr+WNi+vvXn7Nm3b/05cmQzsrLSyMpKY2FhwqlTu7l69fQvhkKLiyO5cOEA7u7riY4+zPffB/P4cVzbvG1tbfarWqjdp+rQ6wukTEx0cXOzJT3dh8rKdOrqsikvTyEz05dlywz58stezJw5GVdXW1JTj/L48cV2r1lenkphYTh5eQFERh7Cz8+OgIAdnDixi5Mnf203QUH7CAlxJDn5CDduhFBWlvDGVqNWjx/HceyYHcbG2ujrqyGRKLNhw0Kys/1obm4poVdXl82FCwdYunQG2tqKaGoqiLAVhHckwrYLqalpKQafnu7D/v0WLFgwjZkzJ6Ojo4iy8jhkZaUZMmQgvXv34ssv/4+RI4e8c9j+0a0/Hh4bGD16KOPHj2TbtmUkJnpx507YL+qatu7XLCqK5MmTeCor09uCtjNtdfkrtYbtkCED+fprEyIjD/Hf/56jpiazrf7rt9+eYc2auUhJDUBfX42tW5dy/rwTRUWR7V7z2bMkrl07y8WLbnh7b2Hr1qXs3LmSffsscHCweoOjozVOTjacPLmLvLzjPHwYS0VFWrvXfvgwFk/PjejpKb1a4GaMu/sGvvsuiKamfGprs6ioSCUhwZPdu1exePF0DAzURdgKwjsSYdtFNDfn8/RpAjduBBMcvJ/16xdgbKzF1KkqaGlNRF19PMrK4xgzZhiDBvWjf/8+jBkz7E+F7R9ZjezuvgEZmSGMHz+SHTvMSU/3oago8o2wLS2NazsB5+XL7nECzm/59T7b1NQ3K0hdvx6Mre18pKQGIJEos2bNPE6f3sOdO+3vSS4tjSMvL4CzZ/exb58FK1bMZNWqWVhammJlZfYGCwtTVq+ejaOjFfHx7hQVRbx1iLqkJBY3t/Voaipgaiph3br5HD9uz40bITQ351Nbm01lZRoZGb4cPmyLpaUZRkZaImwF4R2JsO0iGhtzycnxx919PWvWzMXUVMLMmZNZvXoWO3aY4+RkjYfHejZsWIhEosy4cSNQVBzzwcNWTk6arVuXttuzffw4jvR0H86fdyI/P4BHjy7+YjVyd/RHwvb7789hYzOH/v37oKOjiI3N3N8M25KSGFJSvPH13cqmTYsxNdXDxEQHY2NtjIy03jB9ess2I2srM4KD93PrVijPnrW/9ef3wraxseVQ75wcf9zcRNgKwp8lwraLqK/PITTUkcWLDZBIVF6tANZm714LYmNdyco6xrVrQZw5s5elSw1RVpZFVVXuvcI2MLClcEbry/f1z3p5bUJWdgSystLY2MwhONiBb78986rkYCZVVelcvXoab+/NbNu2jJAQB3744TxlZQnd+gX98zDyICwtTYmJceX69WBqarJobMylpiaLgoJAVq2aRZ8+vdDTU2Lz5iWEhjpRVBTR7jVLSmJITfXm2DE7tm9fzuLFBsydO4XZs1sC99cMDNSRSJSxtDT93bBtHUbW1W3ZE7169Wy8vDa1DSO3jkJkZ/vh5GTN8uUzmTFDVJAShHclwraLqK/P4dy5/cydOwU9PSX09JRYuFAfPz87bt0K5dKlE6SkHMHZ2QYDAzVkZIYwYcKo9wpbf3977O3N8fHZyvffB//is4GBO9HRmYSCwmiMjbXYuHERoaGO3LsX1bZq1s/PjmXLDNHXV8PNzZZbt0J7TNi2VpA6MPogJgAABuFJREFUdGgNqaneVFam8fx5MjduhHD27D7MzCT07fsvzMwk+PtvJz8/gKdPE9q9ZkVFKnfvhnPp0gkSEz0JDXXk3Ln9nD69h1Ondr8hMHAn/v7biYw8xLVrQZSVJb51gVRpaRwBATuYM0fSVrxizZq5pKQc+cW2rOjow6xcOQuJRBktrYkibAXhHYmw7SLq63M4fXoPs2froK2tyNSpKqxePYvoaBfq63P47rsgQkIcsLWdz6RJYxgw4P3nbH19t7FlyxI8PTdy7drZX3z2/Hkn5s6dgrKyLBMnjkFPTwkHB0suXQokNvYwvr5bsbQ0QU5OGimp/mzevLhtZWx3fkG3hm3v3r1QUZHF3NyYc+f28/x5y7afuDh39u2zYMoUFfr2/RILCxMyMnx49CiWly/bD8TWxWQNDblt26rq6rJfHcnXnixqa7NelcfMpbn57YVDysoSCQ11xMrKDIlEmSFDBmJgoE5wsEPbtiwo4OTJXejpKTFq1FAmThwjwlYQ3pEI2y6ioSGX2Fi3toVRampyTJ48AWsrM7y9t7B379esWTMXMzMJ6uryyMvLoK4uj4GBGt7em3n06M1tJe1v/cmksDCczMxjBAbuxN7enKNHt/L99+d+8dnsbD8OHLBh2TJDJBIV1NTGM2/eVLZsWYKlpSnz509l+nR1Jk+ewLRpqhw5spmHD2OprEyjsbH7z9l+/vmnDBv2FWpqcqxYYYSLy1r277fA2soMMzNJW+lGJydrrl8PpqIi9XdrJH8IlZXpXL58kjNn9mJtZYai4hg0NOSxtjLD1XUdnp4bOXp0C0uXzmDUqKFISf0bObmRImwF4R2JsO0iGhvzyM8P5OjRLSxfboisrDR9+vRiyJCBjBs3Ajm5kSgojEJNbTwSiQozZ05m9mwd5syREBBgT2lp3BvXfFtRi3v3oigoCGxb/erv/+acbVFRBKmp3ri7r2fRIoNXJf2kkZaWYsiQgXz1VT/Gjx+Jqakeu3atIjHRk+rqjLaeVkc/zw+lNWz/9re/8dlnn9C7dy+kpAYwevRQRo4czJAhAxk1aijTpqliZWVGcLADpaVxNDTk/mJx2cf7d5VLeXkKJSWx+PpuY+bMycjLyzBu3AhGjx7G2LHDGTduBFJSA/jii8/o2/dLxo4dLsJWEN6RCNsuoqkpj8LCMJKTj+Dispb586eirj7+FXkkEhWMjLRYtsyQjRsXsWfPavbsWc2+fRbEx3u0u/WjuTmfiIhDmJsbYW9vTkFB4KuwjSQ/P4DQUEdcXNZy5sxebt++QHNzQdtw5vPnSRQVRZCU5Imz8xrMzY0xNtZCQ0O+rV1z5kjYv9+CyMhD3LgRQmNj9z2AoFVKijcWFiZtz0BNbTwTJ45m7NjhyMqOYMIEGSQSZdatm09AgD35+QFUVb15SERHSE/3Yffu1cyf33KwhLy8DAoKo1BUHNN2AMHUqSosWKCPnd1yEhM9O6Q3LghdkQjbLqK5OZ/y8lQePIjmypVTxMW5ExzsQHCwAyEhDoSFHSAqyoXERE+yso6Rnx9Afn4ABQWB3LsX1W65vubmApKTj2Bntxx39/Vcu3b21TByGBkZvly4cAAfn62Ehx/k7t0ImpvzqavLpqoqnYqKNF68SHl1lu0pkpK8iIpyISTEoa1dsbFuFBQEcvduOM+fJ3frHm2rBw+iSUnxbnsGZ8/uw9XVli1blmBvv4KDB20ICLAnIcGT69dbKmp1lsAqKYkhLy+A8HBnfHy2vjojeS0eHhvw87MjKGgv4eEHiYtzJyfHn/v3o7r1CU6C8FcSYdvDXb58Eh+frYSEOFBYGE5NTRaFheFkZR3j4kU3QkIcSE31pqQkhqamPGpqMikvT3lVEUm8aH9PY+PPIxKZmb5cvx7Mo0cXO01vtj2VlekUF0fy/fdn+eGH89y7F8nz50md5kuB8OF0x5O4OgsRtj1cSUkM+fmBXLt2lufPk9qGiIuLI7l16zzXrgVRWBhORUVqW63c2tosGhq6dyWov0pzcz7PniVx504YRUURr8pWpnXquc66umx++jGZ0tI4ysoSefEihZcvM3vENEBP1tycT319DjU13b/SW0cQYdvDNTW1VAh6fYFOU1NL5aDGxpaThBobf1m/WPwRvuszbn2eP9eCbm7u+Ha9TXPzz9uNWns54nfe/TU15VNTkym+XH0gImwFQegUmptbVkfX1WXT0NC9V613Rq092+rqDOrqsjtkdXx3JsJWEIRO4fWDD2pqRM+qI7SOwrSMaHR8e7oTEbaCIHQKravdKyvTqanJEgvwOlBL6L45hST8eSJsBUHoNFpPGeruxU86u4aGXF6+zGw7QKOj29Md/H9hGGeQ0Q7oDwAAAABJRU5ErkJggg==[/img]
Das ist ein rechtwinkeliges Trapez. Was ist daran besonders? Kreuze an!
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAZsAAAEpCAYAAABFmo+GAAAgAElEQVR4nOzdeVBUZ7438PvHrXqrbr13mTuZ5J1rMjMJiRsgS0NDA92szdIssojYIItsyiKbLIqgKIKIKIKACIKAKIK0sgiCIghBRVAiSkRRlIhLMDpDMCYxy3zfP8hzMhfCiAp2q7+n6lNlSdN9zuH0+Z7nOc/yL6BChQoVKlRmuPyLvDeAChUqVKi8+YXChgoVKlSozHihsKFChQoVKjNeKGyoUKFChcqMFwobKlSoUKEy44XChgoVKlSozHihsKFChQoVKjNeKGyoUKFChcqMFwobKlSoUKEy44XChgoVKlSozHihsKFChQoVKjNeKGyoUKFChcqMFwobKlSoUKEy44XChgoVKlSozHj5F6ALhBBCyEyisCGEEDLjKGwIIYTMOAobQgghM47ChhBCyIyjsCGEEDLjKGwIIYTMOAobQgghM47ChhBCyIyjsCGEEDLjKGwIIYTMOAqbN8SPP3bg8eNWPH7cih9/7Hhjtmeq7/P3v3fip5/O4fvvT2N09NfX//TTOXz7bTu++aYN337bjqdPz+Dnn8/J/fg87/7/7a/Nv2lkpAWjo6cwOnoKIyMt3P8rynlACENh84Z4/LgV/f2H0d9/GI8ft74x2zPV92GhMjx8HH19ldzrv/22HUNDdRgYqMLQUB0ePmzC06dn5H58nnf/u7v3/6aenjL09R1CX98h9PSUcf+vKOcBIQyFzRvi9u06VFSk4MCBJFy5cuiZd7bsjvn+/UZcuybDwEA1vvmmTW7b87Lv8/33pzE8fBwXLpRi376NqKhIwe3bdRgePo6WllxUV29DS0suenvL8fXXp+T+93re/d++PeI3ZWREYteu1di1azUyMiKRmRmFvLy1qK/PxL17DXLffkIYCps3RGdnCXx9HSCVWuLAgaRn3tmyO+bGxiykp0cgPz8OAwPVctuel32f0dFW9PVVYt++jViyxAK+vg7o7CxBX18ltmwJRVioK7ZsCUVV1TbcuVMv97/X8+4/j6f8m7S0lMHnq4DPV4GWljJEIh4WLRIjOTkYV64ckvv2E8JQ2LwhmptzYWLCB4+njO3bI9DdvR9/+2vzpK9/8OAE2trykZ0dA19fB8TEeKGnp2zatmeqIcGetfz00zn8/e+dL7xff/trM7q792P79gjweMowMeGjuTn3tQ+b7u79CAt1hYkJHyYmfIhEPOjoqGLePCW8885/4733/sDtr4kJH7a2hvDxcUBmZhT6+w/LffsJYShs3hDPGzaseWbtWl+4uFggPNwNn322f9q2Z6rNX+xZy7fftuOnnyY+uH/ZsHndm9HYfjU356K5ORc1NduRl7cWQUEumDdPiTsu7Odtbfno7CyhZzZE4VDYvCT27OP27Tp0dpagpWU3Wlvz0Nqah5aW3ejsLOGeHdy6VYPLl8tx+nQhd3E4dSoP7e0F6Okpw/37DdxFl12E791rQHf3fu792O+dPbsX167JMDx8HN9/f5q7KCsrKyEszA1FRQk4enQHtz3nzhWjr68St2/X4cGDE+jsLMHGjQFwdjaHkZE2pFIrFBdvQHt7AU6dyuO2m4XEkyefYnCwFpcuHURnZ/GEiza7KLLfu3LlEA4cSOLC5sGDE9z/nzlTyO13a2sejh3LxLFjmWhtzZtwHMaHDXv/oaE6XLhQirNn96KnpwwXLx5Ae3vBlMOGdRyY7O/BjgMLN/b3uH+/AT09ZdzP2e+1txfg4sUDGBysxZMnn+Lnn8/h6dMzePDgBC5dOsi9nv09Tp8uQFfX84fCZKE62evG78/p04W4fLkcN25UYXCwFteuyXD27F5uPybbn+++O4179xrQ33/4l3OgBG1t+ROO2+XL5Xj06CRXU3369AwePjyJgYFqdHWVPPM8Hh+ukxl/fsr7OkCejcLmJbFnHxUVKfD1dYBYrAuJRAiJRAixWBe+vg6oqEhBS8tuFBdvQHy8HxYvNueaPSwt9eHoaIqYGC80Nu7E0FAdd6c/NFSH+voMhIa6cu/Hfs/NTYL09Ai0tIxdUNlF+Y9/fBe6umqwsNCDmZkOtz1eXnbYsiUUFRUpaGvLR0nJRtjaGuLjj/+Mjz76AAsWzIFEIoSjoyksLfW57WYXw8HBWpSWJiI21hs+PvZISFiO3t5y7jiw5h72ewcOJEEqteSa0dra8lFRkYLk5GBIpZbcfjs4mEAs1oVYrAsHB5MJx2F82LA7d5ksFcHBLnB1lSAmxgtZWdGoqto25Wa0oaE6yGSpk/492HEIC3VFd/d+7u/R2LgTMTFe3M/Z7zk5mSIy0gOlpYkYHKz95SLbhLa2fMTGenOvZ38PZ2cx/P2dnru5a6phw/4e4/dn8WJzxMf7ITd3DUpLE5GeHgE3Nwm3H5Ptz717Daivz0RmZhRiY33g4+MAW1vDCcctPt4PXV0l3M3Cw4cn0dFRhPz8OPj7Oz3zPB7fbDiZ8eenvK8D5NkobF7S+C//7373n/jLX2Zh3jwlKCt/DFtbETIzo1BYuA6hoa6wszOCUKgJHR1ViEQ8CIWa0NCYB0tLfSQmBqCxcSfu32/45cudgfXr/WFmposFC+bAwEADBgYaUFObA4FADVKpFbZtC8flywfR0LATRkZa+MMf/hvKyh9DIFCDoSEPBgYaWLBgDrS1VeDgYILYWB/U1GyfNGwsLPQwZ86H0NfXQHJyMNra8vHgwQlcvHgAkZEeEAp5mDv3I9jbG6O5ORePH7fiwYMTkMlSYWjIg56eOvLz45CXtxY6OqpcSBw+vBXbt0fA09MWn3zyZy4UxWIBRCIetLVVMH++Eiwt9bFzZxS6ukrw6NFJLmw0NecjJSUEMlkq8vPjEB3tCWNjbYhEPISESCcNm+7u/QgNdYW9vQlCQ12Rl7cWly4dxNmze7FmjTckEiH4fBVoas6HUKjJHa+//GUWfve7/5xQQ0pJWQkLCz2oqs6GQKAGAwMN8Pmq0NNTh7m5HsLCXNHUlIPr14/gwoVS7NkTB4lECGXlj6Gvr85ts76+BrS1VeDpacsdx6ncoU81bNhx+6//+g988MH/YO7cj6CuPhcWFnoICZEiPt4Pq1a5Y+lSCfT01KCmNnZ+6etrQEXlEyxYMBuGhlpYtcodFy6U4vr1IygoWIegIBeIxQKugwKfrwoDAw3o6Khi7tyPYGVlgMLCdbh8+SDu3j2GixcPICsrGn5+jjA11QGfP3bes/NYT08NS5dKkJERib6+SnR1lSA0VMqFipGRFoRCTSxYMBvvvvt7/Md//Dv++Md3YWmpj6KiBAqb1wiFzUsa/+X/n/95F/r6GnBxsUBwsAs2bgxAXt5aJCcHw8rKAKamOoiM9EBe3lrU1GzHnj3xkEolEIl4sLTU5x7Us4ukmdnYnfCKFYtQXLwB5eWbsX69P6RSKwgEali8WIy6uh2orNwCoVATH3zwR5ib62HVKnfs378JxcUbsGLFIpiY8KGmNgfOzmIcP549aTNaUVECFi82h5WVAaKjvbguxO3tBXByMsWsWe/hnXd+BxMTPg4f3or+/sNoa8vH1q1hEAjUYG6uh7q6DNTUbIdIxJs0bFhzX17eWpSUbMCmTYEwNdWBSMRDVJQnZLJUDA3VcRfNBQtmIy7OF1u3hsHFxQLGxtqwsjJASIgUtbXpkzajjQ+bzMwoHD+ejeLiDVzQeHnZISUlBJWVqdi9OxYODib45JO/4Pe//92EGtLixeYwMNCEnZ0RduxYhfLyzdi1aw1WrXKHkZE2LCz0kJKyEvv3b0J+fhxWr14GQ0MtWFkZICdnNWpr01FQsA7h4W7Q0hrbzsLC9VO+aL5o2AiFPERELEV2dgz27duIrVvDsHChEYyMtLB0qQTr1/ujvHwzDhxIQnS0F+zsjLBgwWzY2xvjxIlsfP55BfLz4+Dj4wB19bng8ZQRGuqKXbvWoLx8M1JTQyEUjv29ly93QnZ2DE6cyEZpaSKcnEwhFGrC3d0aGzcGoKIihTuPly6VwMhIC15edmhtzcPdu8fQ1VXCNZc1NOxEZeUWxMX5YsGC2dxNSliYG9rbC6gZ7TVCYfOSxn/5P/74z1i61BpbtoSgrCwJlZVbkJu7BmGhrtDWVoFQqInNm1fi+PFsXLo0ViNZuVLK1RgWLhz7cjc2ZkEiEUJVdTbc3a2Rm7sGN25UcXfYaWnhcHIyxbJldmhszOLCZvbsv8Db2x7FxRtw61YNbtyoQm7uGkilVlBS+hN3cbp5sxqFhev/14WYDRKMifGCk5MZdxE+f34fFx7/+q//in/7t//D1WBOntyF/Pw4hIW5wtBQC66uEu4ZwD82f7GwYRcrdpHt7S3H4GAt6uszsGSJJQwNtRAQ4IzCwvW4ebOaex8lpT9BKrWCh4cNd7FbvtyJ28/JLsLjwyY1NQwlJRuRlBQMXd0FEAjUkJISgtOnC/DVV024dOkgYmN9IBLx8MEHf4RYrMs9e/PxcYCWlgp0ddXg4WGDQ4e24Ny5Yhw7lonNm1dytdRly+wQH++HxMRABAW5gM9XhVgsQF7eWpw6tRtHj+7A9u0RcHAwee6u4c8bNu+++/tfziEbHDyYzA36ZM2QHh42SEwMwMGDyTh/fh/a2vKRmhqGRYvE+Oij92FoqIW6ugwubPz8HKGtrcLVLPr6KjE8fBynTu2Gu7s1BAI12NoaYuXKJcjNjcXGjQFQV5+LOXM+hJ+fIwoK4tHVVYKurhIUFMRjxYpFWLBgDkxNdVBZuYV7dsP246uvmnD6dAFSUkIgEKhhwYLZ8PNz5P7u8v7+k6mjsHlJ47/8GhrzkJQUhJaWXFy7JkNHRxHS0sLh6ioBj6cMfX0NhIe7cYPv0tLCERDgDLFY8MuXm4f9+zehrCwJZma60NVdgISE5WhqysGXXzZygxcvXjyAysotqK7ehlu3arhmNDW1OVi/fjlaWnZjePg4vvyyEU1NOdyd4bPCht3BS6VWMDPT5S5SrFns3/7t/+C//us/oaOzAElJQcjPj0NUlAfc3a25Z089PWWThg1rhmHNR19/fQpPnnyKM2cKsXz5IkgkIqxcKZ0QNv/93/8FJaU/Yf58JSgp/Ylrrunrq8ToaOuUw2bjxgCkpoZxNRFHR1NUVm7hnhGxXnQhIVKoq8+FRCJEa2se2tryYWtrCCWlP8HAQBNLl1ojKSkIu3atQUZGJMLD3aCvrwFV1dmwsNCDr68DkpKCEBGxFOrqc/HRR+9DLBbAz88RCQnLuUGZzzvo9XnD5i9/mQU7OyPupoFNZ8M6WJw4kQ2ZLBWlpYkoKkpAamoYfHwcIBTyMGvWezA21saJEzlcM1pYmBsWLzbnahajo634/vvT6O0tR0pKCJYutcbChcaQSiWIi/Ples2xm4XExEAUFMSjoCAeiYmBcHWVYPbsv0AgUENubiz392T78fnnFUhMDISdnRG0tFRgZ2fEhdw/vo4oPgqblzT+y6+np459+zZyF6/e3nIkJCyHtbUIPJ4yhEIeVqxwxrp1/li3zh+rVy/DypVLsHixObS1VWBjI8LeveuRl7cWQiEPBgaayMqKRk9PGUZGWrjP/eabNgwMVGFgoArffNM2aRfhyS5Ok4UN6wgQHOwCgUANxsZ8JCcHIykpCIaGPHz44Sx88slfYGSkjVWr3BEb641Fi8xgZ2eIgABnrgY2WdiM/zy2P+NDYXzY/Pu//1+8++47mDXrPbz//h8hkQhRXr6ZO85TDRt23IODl8DSUh8+PvZoa8vnHmj/4520rq4aFzZsO95////B1FQH3t4LERPjhYSE5YiL80Vg4GJIJEIYG/P/YR/WISsrGk5OptwzDkNDLUilVggLc8OmTUEzHjasps0G7bJecl9+2Yjz5/ehuno7du1ag6SkIKxd64OgIBcsWiSGQKCOWbP+H1ezY+dLTIwXAgMXY8uWEPT1VXKfN/58Ysdg2bKFUFZWwty5H0EqtcLq1cuwaVMgNm0KxOrVy+DhYQtd3QWwthZhz554rrcg63izf/8mODuLYWCgicWLzZGcHMx12PitrvJEcVHYvKTxX37W7MC+DOzBuomJDrS1VWBiooPAwMXcRS8uzherVy9DWJgb/PwcERPjhfLyzcjMjIKOjuovd3xr0Nd3CKOjv3Y1Zr2jJuu19aJh8/BhEzo69mLbtnDumcvy5YuwapU7XFwsIJEIYW0t4npTublJwOerwtRUB5s2BXI1sOkOm3fffQfq6nOhqTkfs2a9Bz5fBZs3r+Sav543bEJCpLC1NURQkAs6O4u5rrqPHp1EV1cJ0tLCoa2twl1sx9cUwkJdsWHDCu6iGRbqisDAxdxnFBauQ3f3fly8eAClpYlYt84fnp62kEiEMDTUgq6uGrS1VWa8GU1J6QO4uFggOzsG168f4XrJNTXlIDDQGaamOjAz04WtrSE8PGzg42MPNzcJzM31oKT0Jy5s2fmyZo03wkJdkZ4egWvXZNznTRY2fn6O0NJSAY+nDG9ve8TF+SIhYTkX0qtWucPf3wlxcb5oaNjJdbXu7z+MzMwoLF061jTHajRXrhziuqL/1iBgorgobF7Ss7787BmAhYU+tLRUYG6uh/h4P+Tnx6GgYB1yclYjOTmY+xInJgairi6Da7bS0lJGRkYkV7Nh43pu3KhCQ8NONDZm4datGtTXZ8DEhA8+XwXp6S8eNizEDh5MhoWFHubO/QhisQBSqRX8/BwRHOyCkBAp/P2d4OwshlDIw4cfvg+RiIeCgnXcRXN82Mhkqdi6NQzBwUuwcKHxc4fNhx/O4p5x8PkqEAjUsGzZQuTkrMaVK4e4O/VnhU1Cwgps2hSE8HA3SCRCeHvbo6VlN1ezuH+/EY2NWVizxhuqqr82O7a07IZYrAslpT/B0dEUsbHeyMtbi9LSROTmrsGWLaGIifHC6tXLkJYWzj0D+eyz/aiu3ob8/Dhs2xbOdR03M9PFn/88CzzefCQmBnK9/l72fGMmCxs2XqqoKAECgRpXU/PxsUdsrDfWrfNHaKgrHBxMMGfOh7CyMkBzcy7XjBYV5QlfXwckJgbi888ruM9j4eDr64CFC42xeLE5Vq9ehtBQV+jpqcPAQBORkR7Izo7heitmZkYhKSkYq1a5Izk5GM3NY03PfX2VqKxMhVQqgUAw1stvume4IK8ehc1LetaXn30JpVIJ18V5376N+PzzCly/fgRnzhQiJ2c1wkJd4eRkhpAQKT79dA/3QH7sGYw/Nw6BNS8cPJgMDw8bLFtmh+rqbThwYBOMjbWhr6+BjIzIFw4bNnixqSkHjo6m+PDD9/HRR+9DIFBDQIAzkpKCsHXrr888Pvzwfbzzzu9gbKyN2tp07qI9PmwOHdqCpKQg+Ps7wdbW8LnDRlV1Ntas8UZGRiTCQl3h6Gj6S/dvS9TXZ+DGjSp0dBQ9M2w2bQrCjh2rEBPjBaFQExKJEMXFG7iQvHZNhvT0sYf3H344i3uf1tY8SCRCzJ79IezsjLBxYwDa2vIxOFiLGzeqcOxYJsLDl8Ld3YYLnNzcWGRkRCImxgtJSUE4cSKbGxS7a9caCIU8qKvPRUiIlOv197LnGzNZM9rXX59Cb285srKioa2tAm1tFWRlRaOzsxiXLh1Ec3Mutm+P4J6lmJjwUV//awcB1vzo7++Erq4S7vPYTdXChcawtTXEsmULkZYWjnXr/KGnpw5DQy3s2LEKn366B59/XoFLlw7i+PFs7NwZDQ8PWyxfvgiHD29FS0sudu+ORUCAMzQ150NXdwHi4/24IQHy/r6TF0dh85JGRlrQ01OGjIxIrivrP3752WC4tWt9fhn7Mvala2nZjXPnilFTsx2xsT5YssQSVlYG3EX49OlCLF5sznXNTUsLR0PDTjQ353IhweMpQyzWRVlZ0guHDXtgL5Vaobx8Mzf7c2dnMXx87DF37kd4553fQUXlE0RHe6KkZAMqKjYjKSkIOjoL8O67v8esWe/ByckU7e0F3H5Pd9iw96mvz8SBA0lYvXoZNDXnQ0dHFampoWho2Immppxnhg2rdWzfHg5jY22uG+2ePfFoaNiJffs2cj3e3n33He59urpK4O/vBH19DZiZ6WLFikUoL9+Mzs5idHYWY9++jVwz45o13tixYxXS0sK5nn3e3gtRVpbEvZ49k9PQmIewMDeuq/fLnm/jj/8nn/wZnp623PGcLGw6Oopw/vw+1NamIz7eD9bWIvz5z7NgYKCB8vLNOHduLCBZsxjrXXf27F6cO/fr/hsb8+HpaYvExADIZKnIyVkNY2NtCARqWLvWBxUVm7mZB9gzIGtrEaRSK5SWJqK8fDNWrFgEgUANs2a9B03NeUhIWI6jR3ego6MIPT1l+Oyz/bhy5RDu3Wugrs+vEQqblzQ6egp9fYewa9dq8PkqE778bJoPmSwVtraGXG8lV1cJVqxwhpubhBv8aG9vws3We/lyOeLj/bixIGPjFGzg6WnLXXx5PGVufMKLNqOxrshqanPg5WXH3QGP3al6c72Sxi724Whry0NnZzHy8+Ogp6eOWbPeg0CghshID1y8eIDb7+luRmPvc+ZMIa5cOYTKylRIJCKoqc3FokVixMX5/hIi/zxscnNjcf78Pq6rtarqbG5Ap52dESwt9TF/vhLeffcd/Pu//1/ufQYGqpGfHwdv74XQ0lKGmtocODiYwMfHHj4+9li40Bjz5ytBKOQhPT0CR4/uwMGDydiwYQW3/U5OZtzrbWxE+Oij96GtrYK0tHBuEOvLnm/jj//4sJmsGc3d3QYBAc7w8LCFSMTjxhnx+arYtWsNjh3LREZGJPfAn/Wuc3WVwMvLjtt/fX11JCcH4+TJXbh+/Qjq6zNgb2+MefOUIBCowcZGBB8fe+485vNVoa+vAXd3GxQVJWDXrjUQi3Uxa9Z7ePfd33M1yYAAZ0RGeiAmxgvh4W5ITg5GfX0mDep8jVDYvCTWK6y8fDOkUituavvxr2O90hwdTWFhoQexWAAbGxEkEiGEQh5sbUWIjfXh7nDZdCqxsT6wtRVBKORBIhHC0tIAuroLYGioBQ8PW266k8lmWWbNbmz6GLZ9rMaVmBgIe3tjmJnpwN3dmnvwyy6uK1YsglisCzc3CY4cSeMWIWto2AkPDxuYmwsQFOSCwsJ1uHnz1yUKurpKsHy5E1xdJSgtTcTJk7uwb99GpKSEYOVKKReqbNZn1nV2/LQyk+0XC0NnZzE8PGywdu3YsSsqSoCLi/mkSwwcPrwVN2+OzdMVFeUJc3M96OmpQyBQg6mpDoyN+dx4qT/84b+5DgJs2pWcnNWQSi1haDg2CNfaWvTLFCxjMyGwZs3e3nJ0dBShpGQDfHzsYW4ugKWlPqysDGBlZTDh9ayjx3Sdb+y4WVuLEBfnyx1P1kGgsTELy5bZcWONxqaoMYOLiwVsbQ1haqoDgUANLi7mKCpKQG1tOrZtC4eXlx3U1Obgo4/e5zqGsPP5t/aHnff29sYwNtaGoaEWJBIRrKwMoK+vAROTsZoQCw92nvL5KtDX14C5uR5cXCzg7W2PFSsWISDAGX5+jtw+URfo1weFzUtiD9TPnt2L4uINk7a9s+aLo0d3YMeOVYiN9UZExFKsWeON9PQIVFSkoLOzeMLcaJ2dxaioSEF6egTWrPHGqlXuiI/3+2WEdg538Z1slmXWoYBNjMm2j9W4LlwoxaFDKdizJw5FRQlobMzC/fuNXBdgNkK+rCwZ167JuOWVb9yo4sbf1NRsR3d36f+ajfnu3WOorU1HZeUWXLx4gJu+pakpBwcPJnOLe7FnRIODtWhqypkwYeZk+8WWSJDJUnHoUArq6nagq6sE7e17UFSUMOniad3dpbh5sxoXLpQiPz+Oewa1Y8cqZGVFY/v2CKxb54+lS62hrPwx1xuLTSh55coh1NdnoKAgHlu3hmH9en+sWbOMmymCddj4+utTePjwJPr7D+P48axfxpUEIDraE9HRnhNeP9WuvFM939hxY82D7Hiyrs+3btWgunobtm0Lx6pV7ggPd8PmzSuRnx8HmSz1l8HIsSgqSkB7+x6cPLkLW7eGwdvbHiYmOhCLx24yWG/KyfaHnff19RnIyVmNhITliIz0QHS0F5KTg1FYuB7Nzblcsxg7T9PTxxaGYx0K9u5dj+LiDSgtTcTBg8ncPo0fBEoUF4XNS2J3ioODtejtLX9mtZ7dIVdVbUNpaSJkslR0dZVMemfLLi5dXWOTT5aVJaOxMWvCuJtnLZ882c/Z+7Nlhccvpzz+/8e/H5sBYPxyy+z32c9GRlowPHx8wnFiYcOO4fjlmyfbbnbc2ZLP7PfGv//4ZaHZv9va8pGZGfnLBW8dDh3aApksFcXFG7B580r4+TnCwECTmxFh/OeyaXpqa9Mhk6WisXEn+voOTTgO7PV9fYfQ2LgTFRWbUVGxedLXT9f5NtW/z/jzqrt7P+7da+CW12a/f+5cEdLTI7hnbu7uNsjNXfPM/WfYs6bGxiyUlSVzE8JOdl49axlstk803ub1QWHzktid4pMnn3KD0f7ZA0t2h3znTj0GB2sxNFSHR49OTvqlYRfjR49OYmioDl98cRT37zdiZKQFP/xwlnsdq8FM9vmT/Zy9/+joKYyMtHA/n+z/x78fmwHg6dMz+PnncxPel/3shx/O4vvvT084TqwZjR1DVnNi7zfZdrPj/u237fjmmzbu98a/P9sO9vNHj07i+vUjqKjYDDc3Cdcpg9Vw2ANrAwNNWFhM7HLLPpdNQHr37jEMDdXh/v0GjI6emnAc2OtHR0/h/v0G3L59FLdvH5309dN1vk317zP+vPrbX5vx3Xen8f33pzE6+uvv9/VVYvfuWO6ZW0CAM5qacp65/8wPP5zFyEgL7t9vxBdfHOWWupjsvGLPG8cbGWnB6Oiv+0TjbV4fFDbkrcLu6Kurt8HLyw5isQBubhIEBDhj5Uop94DczEwXYaGu3BT78t5ueWPPEBMTA+Hv78QtMfGslVYJYbs+QLUAACAASURBVChsyFuF3dH39VWiuHgDN8hy8WJzODqawtnZHB4etli/fjkaG7O4Ee3y3m55YzMryGSp2LkzigvhZ620SghDYUPeSuwZQlXVNm48THi4G2JjfZCZGcV1YJD3dioKViPs6SlDS0suOjqK8PDhSQobMmUUNuStxJ4h3LlTj6tXZdxgwUuXDqK//zDu3WvAd99RLyeGhQrr6PHw4Uk8fXqGmtHIlFHYEEIImXEUNoQQQmYchQ0hhJAZR2FDCCFkxlHYEEIImXEUNoQQQmYchQ0hhJAZR2FDCCFkxlHYEEIImXEUNoQQQmYchQ0hhJAZR2FDCCFkxlHYTLNfV7isRE9PGbfC4Gefja0yyCZ8vHy5HAMD1bSsLXkhbBG1kZEWfPHFUe58O39+Hzo6itDZWYxLlw7i5s1q/O2vzc+9SBsh043CZpqxRaa2bAlFTIwXQkNdERrqivBwN8TEeHFT2cfH+yE/Pw4tLbkYHj4u9+0mrxe2PHRPTxnKypK48y0gwBnu7jbw8bFHbKw3CgvXobu79LmXnyZkulHYTLO+vkps2RIKqVQCCwt9mJjowNpaBCcnM0illnBxsYCtrSEcHEzg7b0QycnBaG7OxdBQHb79tl3u208UG5vqf3CwFk1NOcjJWY3QUFe4ukoglVrB0dEUFhZ6EIsFsLERYflyJ+TkrEZrax7u32+gpQCI3FDYTLOenjLExHjBwkIfBgaaMDPThZeXHcJ+qd0EBy+Bh4cNrK1F0NJShokJH9HRnpDJUjE0VCf37SeKjTXTHj2ajoAAZxgba0NPTx0SiRDh4W7YtCkQCQnLERTkArFYAD09dVhZGSAmxgvnzhXRImdEbihspll3936EhrpCKOSBz1eFtbUI69cvR35+HAoK1iE3NxZpaeFYuXIJhEJNaGjMg6WlPuLifHHx4gG533myRcXu32/EF18cxc2b1bh5sxp37tTj669PUdu/nD14cAJtbfnYvDkYQqEm5s1TgqWlPkJDXVFYuA719Rmor8/Anj1xCAhwhqmpDubPV4K1tQhHjqQ98xkhLYZGZgqFzTQbHzZSqRXKyzfj888rcP36Edy4UYWrV2VoaNiJuDhfLFxoDA2NeXByMkVTU47c7zzZcsmNjVkoK0tGYeF6FBauR1XVNvT2llPbv5z19x9GZmYkXF0l4PGUYWmpj/z8OHR378fNm9W4d68B9+414OrVSjQ15WDTpkBoa6vAwEADu3fHoq+vEqOjrZO+Py3zTGYKhc00Y2FjaKgFAwNN+Pk54tSp3Xj8uBU//tjBve7evQbU12ciOtoLKiqfwMBAA+Xlm+V25/ndd6dx714Dzp7di927Y7FhwwqsX78csbE+iIhYirg4X+TmrsHx41m4ffso1XAU5PwKCHDG+fP7JryOdSBoaspBYKAzfH0dUFGRgv7+w3j8mMKGvHoUNtOMXQxMTXVgYaGHsDBXtLfvmRA27OJ+4EAS9PU1wOerYteuNXK782Tht2HDCkgkQpia6iAwcDEiIpbCzU0CiUQEIyMt+Pra4/jxLKrhyMmZM4VYssQSWlrKWLzYHGlp4bh6VTbhdaxr9JdfNuL8+X3o7CzB7dt1E87D8agZjcwUCptpxsKG9QaKjvbEmTOFk37Jm5tzYWLCh7r6XGzcGIC2tnw8eHBi0vefqbC5elWGtLRwLFokhrr6XAiFmoiL80VmZhRiY32wZIklVFQ+gbm5ABUVKbh37xi++456z71qra15kEiEUFb+GJ6etsjPj8PAQLXct4uQZ6GwmWYvGjbz5ikhKMgFFRUpuH178l5pM3Xnef78PgQEOEMo5EEsFmDlyiVoaNiJ/v7DuHTpIA4cSMKSJZZwc5OgpmY7hY2ctLTshlisi08++TOWLLFEdnYMrl8/IvftIuRZKGymGQsbMzNdSCRCREZ6oKNjYpdT1szR0LATRkZacg+b9vYCODqagsdThqenLXJz1+DGjSru52MPpqOQlhaOjo4ifPVVE7dP1Nzy6jxv2LCa8DfftOHbb9vpWRuRGwqbacbCxsREB2ZmuggLc8P58/smXJTZA9zKyi0QCjXl3ox26lQeLC31weMpY906fzQ15eDLLxu5nz9+3Ir+/sO4elWGhw9P/q8LGD1IfnWetxmNjcsZGKjC0FAdPWsjckNhM81Y2Bgb82FszEdoqCu6u/dPeN3XX59Cb285srKioa2tAm1tFWRlRaO3txxff31q0vefqbBhzXmamvORkhKCjo4iPHx4kvs5u2jdulWD4eHjGBlpwejoKQqbV+x5OwjculWD6uptOHBgE5qbd6Gv7xBGRyc/vwiZKRQ202yqYXPnTj2qqrYhLMwNyspKEAjUUFSUgMHBWjx58umk7z9TzWgsbBYsmI24ON8JNRs251tx8Qa0tOzGtWsyjIy0UDOanM6vqXZ9bmzMwrJldnBwMEZycjAaG3fi/v0Gue8HeftQ2EwzdjEwMtKGSKQFX18H1NVlcCPxxw/qtLc3AY+nDCcnUxw9ukNuzRzt7QVwcjKFtrYK/PwcsXt3LD77bD83k8CJEzmIivJESIgU+/ZtRHf3fvztr81yP95vm/GDOiUSIYqLN6C3txyDg7W4e/cYhobqcOXKITQ35yIpKQgaGvOgpjYH69f708SvRG4obKYZCxuRSAsCgToWLjRGYmIgNxJ//HQ1PJ4y7O1NsGlTEC5ePCC3B7gXLx5AZKQHLCz0YGqqAy8vOxQXb+BmEoiP94OhoRYsLPSQnR1DYSMn46erWbBgDqRSKyQkLEdpaSJqa9Mhk6VyE3Sam+vhgw/+OOVBw4TMFAqbaTbZRJxsqYHAwMXw8rKDvb0x9PXVIZEYYN06f9TWpuPu3WNy2+7BwVqUliYiLMwVFhZ6MDfXQ0iIFGvX+iAkRIolSyyhr68OJydTlJYmPnMkOpkZ7NlZTc12+PjYw9BQC6amOnBwMEFg4GJERnogLMwV3t4LIZEIuQHDvr4O6Owskfv2k7cXhc00m2yJAXt7E9jbm8DBwQROTmbw9LRFdLQncnJWo7k5FwMD1fjmmza5bfeTJ59icLAWR4/uQFiYKywt9aGruwA83nzo6CyAlZUBli93QlZWNC5ePPDMkehkZrAOIv39h1FRkYKEhOVwd7eGmZkutLSUsWDBbGhozIO+vgasrUXw9rbH+vXLn9mlnpCZRmEzzSZbPG38ImppaeGoqtqG7u79uHevQWF6dbEaTmSkB5ycTGFpqQ9HR1NuVuHxvdSIfLCu6I2NWUhPj0BwsAvs7Y0hFo+N73J1lSAmxgu5uWvQ1JRDNVEidxQ202yyZaHHLw999aoMd+7U429/bcZ3351WmF5drIZz8eIBtLcX4NSpPLS3F3CzCj98eJLGaSiAH3/swOPHrbh/vxHXrslw4UIpPv10D1padqO1NQ9nz+5FT08ZbtyowpdfNlJNlMgdhQ0hhJAZR2FDCCFkxlHYEEIImXEUNoQQQmYchY2C+OGHsxgZacGdO/W4elWGnp4yfPbZxI4F4/9/przqz5P35yrK50+2HZcvl2NgoJoGZZLXFoWNghgZaUFPTxmqqrYhLS0cMTFeCA93m9Blevz/z5RX/Xny/lxF+fzJtiM+3g/5+XE03Qx5bVHYKAg2Pmf9en+4ukogkQhhZ2fEDQZ1cjKDVGoJqdQSTk5m3P/PlFf9efL+XEX5/PHb4ewshqWlPqytRfDyskNqaig6O4sxMtKCH344K/fzlpCporBREJ9/XoHExEA4OZnBxIQPCws9LFu2kLvTDfvlbjc83A1hr+DO+lV/nrw/V1E+f/x2+Ps7wdbWEPr6GlBTmwNbWxHy8taip6cMIyMtcj9vCZkqChsFMX7RNVdXCTZvXslN4EneTpmZUYiN9YFUKoGm5nzo6i5ASIgUpaWJuHq1UmFmniDkWShsFAQLG9ZcsnnzSrS25nFLE5C3U3//YVy6dBCVlakICHCGpaU+zM31EBDgjKNH0zE0VIdvv22X+/lLyLNQ2CgIFjb29iYIDXVFYeF63Lw5+XK/5O3C5qwLDR1bmM/cXA/x8X6ort6GW7dq5LY0BSFTRWGjIChsyD/D5qw7fHgrPD1tIRCoQ1d3AZYts0NjY5bcFt0jZKoobBQEhQ2ZirGVOqPg4mKB+fPHlhNPSQlBe/sefPllo8JM6ErIeBQ2CoLChkwFW1pg376NWLjQGFpaKrCzM0JCwnKcP7+POgwQhUVhoyAobMjzYIv0ubhYQCTiYdEiMfLy1uLChVJ89VUT1XCIwqGwURAUNuR5jI62oq+vEvv2bYSLiwWEwrHASUwMxIULpVTDIQqHwkZBUNiQF9HbW46EhOWwsRGBz1eFra0hsrNj0NVVgkePaEVVojgobBQEhQ15EV9+2Yimphxs3BgAoZAHZWUlmJsLEB/vh8uXy+W+fYQwFDYKgsKGvAi2DHltbTr8/R0hEKhh3jwlWFuLUFaWhMHBWjx58qnct5MQChsFQWFDXsRPP53Dt9+2Y2CgCrW16Vi71gcCgRp4PGUEBi5GaWkiBgdr5b6dhFDYKAgKG/IyxtdwzMx0IZEIERrqivr6DJrWhsgdhY2CoLAhL2N8DWf9en+YmenC2Fgb0dGekMlSMTRUJ/ftJG8vChsFQWFDpgOr4Rw5shWurhLo62vA2lqEqChPnDiRg3v3GvDdd7TSJ3n1KGwUBIUNmQ6shtPTU4b09Ai4ukqgpaUMQ0MtxMf7ob4+E/fuNch9O8nbh8JGQVDYkOk0PHwcLS25SElZCUtLPfD5KnBwMEFCwgq0txfg4cOTNHEneaUobBQEhQ2ZTt9/fxrDw8fR3r4HKSkrIZVags9XgaWlPnbsWIWOjiI8fEiDPsmrQ2GjIChsyExgNZzk5GCYmPDB56vAy8sOmZlR6Ows5mo4f/97J3766RzNqUZmDIWNgqCwITOB1XCam3MRHe0JiUQIPl8FtrYiZGZGcTUc9qyH5lQjM4XCRkFQ2JCZNDRUB5ksFatWuUNPTx08njI8PW2RnR2Dy5cP4vHjVjx+3EphQ2YMhY2CoLAhM4l1ia6ry0Bw8BIYG/PB4ylj8WIxZLJU3L59FI8ft1IzGpkxFDYKgsKGvAqDg7UoLU1EUJALdHRUIRRqIi7OFzU129HffxiPH7fixx875L6d5M1DYaMgKGzIq/DkyacYHKxFTc12BAW5wMJCD6amOvDxsUdFRQoXOPLeTvLmobBREBQ25FX6xxoOn68KXV01hIW5oawsGdeuyejZDZl2FDYKgsKGvEqshlNRkYJFi8RQVZ0NTc35cHOT4MiRNJq4k0w7ChsFQWFD5KGvrxJbtoTCzs4Ic+Z8CD5fBevX++PEiWzcvXuMOgyQaUNhoyAobIg8jI62oq+vEkVFCbCzMwKPpwxraxHi4/3Q1VVCzWlk2lDYKAgKGyJPrIbj7CyGQKCGhQuNkZ8fh56eMoyMtMh9+8jrj8JGQVDYEHliNZyCgniYmwugrj4XLi4WSE+PwLVrMrlvH3n9UdgoCAobogguXChFcLALDAw0oaurBldXCcrKkqlLNHlpFDYKgsKGKAI2rU1kpAcMDDTB4ynD1VWCzMwo9Pcflvv2kdcXhY2CoLAhiuDx41b09x9GeflmeHnZcTWcpUutIZOlYnCwFk+efCr37SSvHwobBUFhQxTBjz924PHjsec35eWbuRqOQKCG4GAXlJYmYnCwVu7bSV4/FDYKgsKGKBJWwykrS4KrqwQGBpqwsNBDSIgUtbXpVMMhz43CRkFQ2BBFwmo4PT1l2LVrNfz8HGFgoAmRiIeQECnVcMhzo7BREBQ2RBE9fHgSHR1FyM6OgbOzmKvhhIe7oaVl97St9MkWbxsZacHw8HFaQfQNRGGjIChsiCJ6+vQMHj48ia6uEmRnx3A1HIlEiIyMyGlb6ZOtt9PTU4aWllxaQfQNRGGjIChsiCIbX8MxNxfA398JmZlR6OwsxvDwcYyMtLxwKDx6NBZoMlkqdu6M4prpKGzeHBQ2CoLChiiy8TUcf38nGBryYGsrQmZmFM6e3Yvh4eMv3NzFxvckJgbC398JCQnL0dtbTs1obxAKGwVBYUNeB6yGs317OExMxpaW9vS0RXZ2DC5fPvjCNZCbN6tRWLie+w4EBy/B6dMF+PrrU3j48CQePTqJb75pw9OnZ/Dzz1TDeR1R2CgIChvyOmA1nObmXISGusLYeCxwFi8WQyZLfeF1cMaHjb+/E2pr09HbW46OjiJ0dZVgYKAKDx824enTM3I/DuT5UdhMM9Zl9FlruY9vHqCwIa+Tf1zpU0dHFQYGGlizxhtVVWm4caPquWs4LGyCg5fA0lIfCxcaIzExALt3xyI9PQI7d0Zh//5NaG7Oxc2b1c/9/ZL38SIUNtOODYZ71sSF4x98UtiQ1wlb6bOmZjuCglxgZqYLAwMNeHjYoKrq+Vf6ZGHj7+8EHZ0FmDdPCQKBGkxM+DAz04WlpT5sbQ0RGuqKw4e3Pvf3S97Hi1DYTBtWo7ly5RAOHEhCRUUKbt+um/T1FDbkTcBqOCtWLIKa2hzweMqIjvZ87hoOCxsfH3uoqc2BktIHMDDQhI2NCIsWmcHGRgQ+XxWWlvpITAxEQ8NO3LlTP2nNhcJG8VDYTBNWozlwIAlSqSV8fR3Q2Vky6eupGY28CVgNp7x8MxwcTKCs/Al4POXnruGMDxsDA02kpYXj+PEstLXlo6RkI9zcJDA314OHhw3S0sJx8eKBScOEmtEUD4XNNPnbX5vR3b0f27dHgMdThokJH83NuVP+fQob8jpjK33a2RlhzpwPweerYP16f5w4kY27d48986I/vhnN0dEUTU05XJhcunQQsbE+sLYWwcSEjxUrFqG1Ne+Zz26I4qCwmSYUNuRtxlb6LCpKgJ2dEXg8ZVhbixAf74eurpJnNmeN7yDg5+eIjo4iLqT6+w8jMzMKUqkV1NTmwMZGhGPHMilsXiMUNs+Jdf0cGKhGV1cJWlvz0NKyG0eP7kBRUQLCwtygrKxEYUPeSqyG4+JiAZGIh0WLxMjLW4sLF0rx1VdNk9Zwxnd9Dg11RXf3/gk/9/Kyw9y5H8HEhI/6+gx6JvMaobB5TmxQW35+HPz9nSCRCCEW68LMTAcWFnrQ1VXDH//4LoUNeSuxGs6+fRvh4mIBoXAscBITA3HhQumk4TDVsPH2toeKyiewsjJAc3MuPZN5jVDYPKcbN6qQm7sGPj72EAp50NCYB6FwbOp1Pl8Vc+d+hHfe+R2FDXmr9faWIyFhOdeLzNbWENnZMejqKsGjRycnvH58M5qPjz3a2vLxzTdt+Pbbdly6dBCpqWM1Jh2dBXB1leDs2b1y308ydRQ2z6mjowgeHjbQ0VGFjY0IYWFuKC1NREnJRgQFuUAo5GHWrPcobMhb7csvG9HUlIONGwMgFPKgrKwEc3MB4uP9cPly+YTXj+8gYGMjQkXFZgwMVGFoqA7Hj2fBx8ceIhEPlpb6iInxQk9Pmdz3k0wdhc0UsXE0NTXbIRLxMH++EkJCpNwUHWNflnXw9LTFJ5/8mcKGvNXYkgG1tenw93eEQKCGefOUfgmRlAldosc3k7HxOgUF8di3byM2bQqEqakO9PU1EBi4GMXFG3DrVo3c95NMHYXNFLFxNHl5a6Gjowo9PXXs27eR+9KM9UYrxfbt4dQbjbz12KDKgYEq1NamY+1aHwgEauDzVRERsZS7SWOvH98B4L33/gAVlU+gq7sAenrq0NZWwfz5SrC2FmHv3vXo66vE6OjkMwgQxUNhM0VsvY2tW8PA482fECZjvdSaUFm5BUKhJoUNIfi1hlNTsx0+PvYwNdWBnZ0RVq1yR11dBgYHa/Hkyae4d68B9fWZSE4OhlRqCRMTPkxM+BCJeNDRUYVQqAk7O6Mpd6UmiofCZoq++qoJp08XICkpCBoa8yaEyc8/n8PTp2fQ0LATRkZaFDaE4NcaTn//YVRUpCAy0gNCoSb09NQRHLyEWyTtu+9O4969Bly5cghnzhSiuTkXzc25qKnZjry8tdizJx4NDTtx+XI5Hj06Sb3QXkMUNlPEujxv2RICLS1lGBtro7Y2nRtUxsbfyGSpMDTkQSzWRUvL7im/P4UNeZOxZujS0kQ4OZlCS0sZZma6CA93Q0vLbjx8ePI3lw6Y6sS2RPFR2EzR11+fQm9vOXbtWs11dS4oWMd9CVgYbd0aBoFADRKJEK2teVN+fwob8iZjHWwuXjyArKxoeHsvhL6+BiQSITIyItHRUYSHDyd2iZ7qkh1E8VHYTBFre66s3AJHR1MYGWlj1Sp3FBauR3NzLhobs5CeHgFPT1soK39MYUPIb2A3ZVlZ0XB0NIWpqQ78/ByRmRmFzs5iroZDE2m+eShspoi1PXd0FCEy0gPm5nrQ01OHiQkfnp628PKyg5mZLpSVP8Z7771DzWiE/AbW3NzRUYS0tHC4u1tDKNSEra0ImZlRXA2Hlgh481DYPCe2fkdoqCtMTPjQ1laBhYU+bGxEEIsFEArHes/QEgOETG54+DhaWnKRnBwMExM++HwVeHnZcTWc4eHjGBlpobB5g1DYPCe2fkdzcy62bw9HZKQHwsLcEBvrg8zMSOTlrUVmZhQtnkbIP/H996cxPHwczc25iI72hEQiBJ+vwtVwzp7di+Hh49SM9gahsHlBrCmgqmobSksTIZOloqurBH19h9DTU0bLQhMyBUNDdZDJUrku0To6qvDxsceuXavR01NGHQPeIBQ2L4i1Pd+5U4/BwVoMDdXh0aOTGB09hZGRlmd+SagZjZBfO940NOxEZKQHbGxEEAp5cHWVoKwsibo8v0EobBQEhQ15m7EaTlSUB0QiHgwNtbB69TLIZKm4fv0IPbt5A1DYKAgKG/I2Gz9xp6np2PpQwcEuqKvbMWHiTvL6obBREBculCI4eAlsbQ0REiKlsCFvpYGBauTnx8HPzxEGBpowNdVBXJwvamvTcffuMblvH3lxFDYKoqurBP7+TrC01Edw8BIKG/JW+uabNgwMVOPgwWQsXmwODY150NZWwfLlTujqmnwoAVF8FDYKorOzGD4+9hCLBQgKcqGwIW+1vr5KbNkSCjs7I8yZ8yFEIh7y8tbiypVD+Ntfm6lL9GuIwkZBUNgQ8qvR0Vb09VWiqCgBdnZG4PNVsWiRGMnJweju3k8dBl5DFDYKgsKGkIk+/7wCiYmBsLMzgpaWCiQSEbKyotHZWYwHD05QDec1QmGjIChsCJmIrSOVkhICgUANSkp/gqmpDmJjvdHZWUw1nNcIhY2CoA4ChEzEVsBtbMzCsmV20NSch9mzP4SFhR5yc9egp6cMIyMtct9O8mwUNgqCuj4TMhFbAffWrRpUV2/D6tXLoKu7AKqqs7F4sTnS0yNw7ZpM7ttJno3CRkHQoE5CJjd+0KdIxINAoAZ3dxtUVW2jQZ+vAQobBUFhQ8jk2MS1AwNVqK1NR3y8L0QiHgwMNBEZ6QGZLBVDQ5PPsk7kj8JGQVAzGiHPxmo4VVVpcHe3hkjEw8KFRoiO9kR9fQYGB2vx5Mmnct9OMhGFjYKgDgKEPBur4fT2liM3dw3XpGZsrI3QUFeUliZicLBW7ttJJqKwURCs67Ox8dgy06mpYWhry8fNm9W/aXCwFnfu1OPBgxN4/LgVT5+ewc8/UxdQ8nZg60llZ8fA2VkMAwNNWFjoITzcDS0tu/Hw4Uk8fXpG7ttJfkVhoyBY2OjpqcPKygA+Pg5ITQ1DYeH631Ramoiqqm1oa8tHf/9hPHzYRF8u8tZg60l1dZUgOzuGm7hTIhEiIyMSHR1FePjwpNy3k/yKwkZBsGY0oZAHiUT4zLApLt6AsrIkVFdvQ0tLLs6dK8Jnn+3H1asy3LlTj5GRFvzww1m57xchM4nVcHbujMLChUYwMtKGr68DMjOj0NlZjK++auIGftJMA/JFYaMgWAcBiUQIb2/7Zzaj9fVV4ty5Ihw7loni4g1IT4/Ahg0rkJYWjqqqbTTYjbwVWA3n9OkCJCYGwtnZHHp66rC1FSEzMwqnTxdw3aJppgH5orBREM/b9Zn1yunqKoFMlors7BgkJgYiJWUlSksTcfx4Njo7i9HXV4kvvjjKtWGPX45a3vtNyHS4d68B9fWZiIvzhVCoCR5PGZ6etlwNh5qZ5Y/CRkE8b9iwXjmPHp3E0FAdrl8/gs8/r8D58/tw6tRuVFSkIDU1FFu2hKCsLIlrw2a/R3d65E3y3Xence9eAxoadmLlyiUwNuaDx1OGs7MYFRUp1CVaAVDYKIjpGmfz+HEr+vsPo7ExC+npEUhKCkJ+fhyqq7fh7Nm9/1DToTs98uYZHKxFaWkigoJcoKOjCqGQh/Xr/VFfn4GbN6vpJkuOKGwUxHSNs/nxxw48ftyK+/cbce2aDF1dJTh5chfKypKwZUsIMjIi0dKSS3d65I305MmnGBysRU3NdgQFuUAiEcLaWoTQUFfU12fQtDZyRGGjIGZqUOf4mg5rVmttzUNfXyWGh4/j++9Py33/CZlOrIazcuUSGBhowthYG+vW+aGmZjv6+w/j8eNW/Phjh9y3821CYaMgZmq6mvE1nZaW3di9Oxbp6REoLk5AS0suhoePy33/CZlOrIZz8GAy7OyMoKz8MfT01OHjY4+KihQucOS9nW8TChsF8aom4hwaqoNMloqMjEikp0egtDQRFy8eoBHX5I3U21uOhITlsLTUx7x5ShAI1LB2rQ/q6zNx716D3LfvbUJhoyBeVdiwLtNnz+5FcXECcnPXoLJyC424Jm+kr78+hd7ecuTnx8HSUh/q6nOxcKExkpODceXKIblv39uEwkZBvOolBoaHj6OlJRdlZUkoLk5AVVUaenvLqYZD3kishmNvbwxjYz7c3W1w8GAyrl2TYWSkhcadvQIUNgriVYfN99+fxvDwcfT0lOHIkbRf5lpLoxoOeSOxGk5h4TrY2xvDGesvlgAAIABJREFUwEAT7u42SE+PQE9PGXWJfgUobBSEvBZPY3NLHT68FYWF61BZuQVXr8qotw55I128eACRkR4wM9OFvr4GliyxRGHhOpre6RWgsFEQ8gobNrdUd/d+FBauQ25uLJqacqi3Dnkj3blTj6qqbYiJ8YJQyAOPp4wlSyyRnh6Ba9dkct++NxmFjYKQ90qdbG6poqIEbm6127fraJ0c8kZh484qKlLg42MPkYgHgUANS5daQyZLpcHOM4jCRkHIe6VONrdUe3sBduxYRRMYkjcSG3fW338YNTXbER/vywVOcLALrfQ5gyhsFARbPE0sFiAoyEVuy0KzkddZWdGoqkpDd3cp/vbXZrkfH0KmExsCUF29DV5edhAKeRCLBQgOXoK6OprWZiZQ2CgIRQkbNvL61KndyMqKRmHhOrlsByEzic1+3tdXieLiDdzEnXp66li1yh0yWSqGhurkvp1vEgobBfGiYcOaBR48OIHbt+tw714Dvvvu5ec6u3ZNhvT0CGzdGoYLF0qf2TuN1skhr6ORkRb09JRhz554ODmZQiBQg0QiQkyMF1pb82jc2TSisFEQLxo2rP25rS0fFRUp0zYNx61bNSguTkB2dgxOnMh+Zu80WieHvI5++OEsRkZacPHiAezZE4+AAGcIBGoQi3WRnh5B486mEYWNgnjRDgJjMwHsxq5daxAevnTapuFgMwyUl29GWVkSmppy8OWXjZO+nsKGvM5YDSc/Pw729sYQiXjw8bH/h44yVMN5WRQ2CuJFuz6P1UA2IDBwMQwMNCCVWuLMmcKX3h42w8DZs3uRkRGJ3Nw1uHGjatLXUzMaeZ2xGs6FC6XYuTOK6xZtaytCZmYU1XCmAYWNgnjRQZ1sFufYWB/Y2oqwfLkTurpKpm27rl8/guzsGGRkROKzz/bTsxvyRmMzaqSnR0As1oWOjip8fOyRk7Ma3d37MTLSgh9+OCv37XwdUdgoiBcNG9aFs7OzGBUVKaitTcfdu8embbvu3j2G2tp0bsE1enZD3mRsRo3W1jzExHjBxkYEoZBH09pMAwobBfGyMwiw0Jnu8QGsLfvEiWzIZKn07Ia8FViLQXS0J4yNtSES8RASIkVRUQJ6e8tp7sAXQGGjIF52BoGZusiPb8umZzfkbcBu3urrMxAa6gpLS32IRDy4u1vj4MFkmjvwBVDYKAhFGdQ5matXZUhLC0daWjiuXqUJC8nbgc2oERTkAj5/bNBndLQnZLJUXL9+hGrwz4HCRkEoetjcuFGF3NxY5ObG/tOaDSFvEjajRkVFChYtEoPHU4axMR/BwS6oq9tB09o8BwobBSHviTifhd3hlZRsRH//YZoNmrxV+voqsWVLKBYtEoPPV4VYLMDGjQFoaNiJO3fqqdl4CihsFIS8lxh4FrYOSEVFCi5dOkizQZO3yuhoK/r6KlFSsvF/BU5kpAc6OoqoOW0KKGwUhLwWT5sqNqPA0aPp6OjYi4GBKnzzTZvct4uQV4nVcBwdTaGhMQ/m5gJkZ8fgwoVSfPVVE9Vw/gkKGwWh6GHDukCfOrUbTU056OoqwaNHNKKavF1YDWfPnniYmupAWVkJtraGSEwMxIULpVTD+ScobBSEojejsa6g58/vQ1XVNjQ2ZuH+/cnH2xDyJmM3hwYGmtDQmIeFC42Rnx9Hgz7/CQobBaHoHQTYOJ6rV2UoLU1EWVkyvvjiqNy3ixB5GFtGPQNxcb4wMNCEuvpcuLhYID09Ateu0dCA30JhoyAUPWwY6gJNyK81/aNH0xEQ4AwjI23o6CyAVGqF8vLNGBiopmea41DYKAhFb0ZjaHAnIb/W9AcHa9HUlIPExEDo6alDTW0OvLzskJ8fh4EBxfv+yhOFjYJgYSORCOHtbY/U1DC0teXj5s1qhdLUlIPVq5dh9eplaPr/7Z35V1RXtsff3/Bed79e3W8lq2MSB0CRgmKsQgrBogRkHlUICBVFZBBBUARBURShUUAUB1QGUVFAIaIyaBwwGJVIgmPUOIXEdKMmnZisXp/3g7mVpEi1JoJAcfZan1+Kupdz7617vufss/fZx0qGvD0CwVBy+XIt587tYtOmNJydrRkz5jUsLU2YM8ebxsbCAaucawwIsRkmSG40hUKGRqMgMtKbNWvi2bYtY1ixevUCZs1yZ9Ysd1avXjDk7REIhpItW9IpLU0jI0OLr+9ULC1NGDPmNezszFmyZM6AVc41BoTYDBOkmY1SKWPKFCs8PByJjvYlISGU+LgQ4oYJkZHeuLs74u7uSGSkt8HvxceFkJAQOuza/1sxlusw1usZLtcVHe2Lv78LSqWMN998HQuLCcyd609FRTa3bh0UG9QixGbYcOlSDenpUcyY4YSrqx1qtT3+/i4EB6vx9Z2Kl5dqWODu7oiLiy0uLra4uzsa/J6v71SCg9XDrv2/FWO5DmO9nuFyXR4ejqjV9rpAAY1GydKlc6irW6fbzma0l94QYjNMkPYey8zUkpQ0m4SEUFJSwklJCSchIXTIR46/eaQZH0pS0mySkmYTHz/y2i8x0p+DsV/PcL2uzEwtFRXZunLSo1Vsfj6jE2IzTJB2l+3uruHixSouXKikq6uarq5qLlyo5Pz5kcW5c7vo6Cino6Occ+d2DXl7fi8j/TkY+/UM1+vq7q7h1q2DPHzYwtOnp0etG+3nIivERjAoGBrJjdaXTiAYjQixEQw6hkRltLoTBILRiHCjvQKkcsp37zZx+XItV67U8uBB83Nrlxv7yF+Izcvdt0eP2nn4sIWvvmrh669PiLpCIwTp+fX2HqGnZ59Bt9+lSzXcuFFPb+8RvvvulFH1B0JsBglpl+S6unXk5SVQUJBIc3PRc2uXG3tnbEwvz6tE2h6lu7uGjo5yOjt3cuNGnagrNEKQnl9bWym5uXEGAxrS06MoK1tKW1spvb1HjKo/EGIzSNy79x4HDxaQlTUXP7+pBAWpyc9PpK1tE729RwweZ0w/LsHLI21p39paSlXVCoqKklm9egFr18azdWs6TU2FfPLJXt1C9FC3V2DoObbT07OXXbuyCAychkIhw9tbpQvV9vScgkajxNtbRUTEDFatiuX48c3cudPIV1+1GEV/IMRmkLh27QDFxSmEhmowNx+HTGaCVuvHjh3LuXmzweBxYuQv+DlSsa6gIDUqlRwrK1MsLCYgk03AxmYiwcFqSkoW60Jsh7q9gl9H8nQUF6fg6GiJmdnbhIRodEmoc+f6M2uWO9OnK7G0NMHFxYaMDC2NjYXcudNoFP2BEJsB5t//PsvTp6f54IMdJCbORKGQMX78G5iYvImrqx1LlkTy4YcVwtcu+I88fXqahw9baGwsxN/fFTOzt7G1nYSjoyVOTlbY2ZkzYcIY7OzMmT8/SJepPtTtFvw6//xHK+fPV5Kfn4hMZoKp6VskJ4frtr0pLU0jLy+BmJhArK3NsLCYQHCwhvXrF3H16v4hb/9AIMRmgHnWSRyjoSEfDw8l48e/gUIhQ6mUYWLyJl5eThw8WCB87YL/yMOHLXR0lLN2bTx2dubY2k5i9eoFNDYWcvRoCbt2ZbFgQTD+/q4EBk4jM1NLd3fNkLdb8Ovoi429/WSqqlbqNvS8fr2Oy5draWjIJyYmEI1GiafnFNLSIvnoo91D3v6BQIjNAPPoUTvd3TWUlCzG3t4cU9O30Gr9iI72ZcKEMdjYTKS4OIXu7hoePWof8vYKhieS2BQVJePr60xwsJqqqpVcvFhFd3cN7723ntTUCPz9XVCr7YmLC+H8+cohb7fg15HcaIWFSVhamqBUymhoyKevr43Hj9t1UYYnTpSRmDgTDw9HZsxwEmIjMMzdu03U1a0jOTkMOztz3NwcqKpaya5dWUyZYoWFxQQWLpyl2zNpqNsrGJ5IbrSLF6uoqMgmPz+R/PxE8vISWL16AQkJoWg0CmxtJ6FUyoTYDHOkAIGNGxcjl5tibW3G5s1L6Oqqpqdnry7KcPPmJbi7K7G1ncTMmdOFG01gmCtXaikoSGTWLHecna2Jjvals3MnHR3lzJo1HTs7c4KC1KL4mOA/IuVpXbpUQ2XlClasiCE+PhSt1het1pfgYDccHS2Ry81QKITYDHf0xWb8+DHExARSWJjExo2LdVGGUVE+mJm9zaRJ44iJCTSq8utCbAaYCxcqfxx1KgkIcCU7ex4ff7yH7u4aMjO1eHk54eQkZ+5cf86d2zXk7RUMTyS3y9atywgIcEWhsMDTcwphYR7ExYUQGxtEcLAb7u5KXFxshdgMc/TdaH/4w38zfvwYLC1NkMtNdVGGY8f+jT/96X8wNx9HWlokzc1FPHjQPOTtHwiE2AwQP/zQwZMnxzl6tITAwGlYWZni7a0iNTWCAwfyOHAgj9TUCDw9p2Bm9jYeHo40NhbS19fG99+fGfL2C4YXUp5WSko4crmZrtxwdvY8iotTyMtLYO5cf3x9p6LRKIiPD+XcuV1GESJrjOgHCPzv//4RmcwElUr+C2xtJzF27N+Qy015993np0qMJITYDBBPnhzn6tX9bN26DEdHS15//a9YWZmi0SgICdEQEqJBo1FgaWnK//3fn7GzM2fDhmS6uqrp62sb8vYLhhdSnlZEhBcqlTXBwW7U1Kzi44/3cO3aAQ4f3kBsbDAajYLp05UkJc2mo6PcKJL/jBF9sZHJTMjPT6S1tfQXlJdnEhXlg0olRy435Z13PDl7dseQt38gEGIzQHz+eTPHjpWQkaFFLjdjzJjXcHa2xs/P5Rc4Ocl57bW/YGb2FgkJoSJQQPCrXL9eR2lpKlFRPjg7WxMQ4Ep5eSanT2/j9Olt7NyZRWioBnv7ySgUMubO9efkyS1CbIYp+mKjUslpbS3t9z1pkBEUpOatt15HpZLT1FRoFM9ViM0AIXUOERFe2NtPxtnZmqVL57B585JfkJwchkxmwtixf8PbWyUCBQS/ijR4yczU6lwr06bZERSkJihIjbu7ErncjLFj3+D11//KjBlTaG/fJNxow5QXFRvJfSr1E05OVlRVreDOnUb+9a+TQ34dL4MQmwHi4sUqkpJm4+bmgJubA3Pn+rNv3xo+/LCCzs6ddHbu5MMPK6iqWklQkBorK1Ps7Sczb14AZ85sFzsKCH6B5Jatrs4hNFSDg8Nkpk610SX7+fg4ExDgiqfnFBQKCyIiZnDy5FbxOxqmPC+pU+Ls2R1s355BbGwQlpYmTJtmx+7dOUJsBD9x8uRWfH2dkclMCAvzoKgomYsXq/jyy2Pcu/ce9+69x5dfHvvxB5dAcLCaSZPGotEoqK9fJ3YUEPwCKeDkypVaDhzIY9OmNDZuTGXLlnR2787h0KG/096+icOHN7BlSzoVFdlcvFglfkfDlOdtVyOxalUsISEaHBwsmDBhDD4+zhw7ViLcaIKfOoXGxkKmTbPD0tKE1NR3aGoq5P79w/12ce7tPUJbWynZ2fOwszNHpZKzbdsyrlyppa+vTbhBBL9A2pq+p2cvXV3VPys3/ExUpBmQ/udD3e7RiqGNdPU34jQ1fYugIDXxcSEkJITqNuQMC/PAyUmOjc0knJ2tSUqazcWLVUN+XQOBEJuXRHrZd+3KYsYMJ6ZPV7Jx42LOn6/gn/9o7ffj++67U/T2HqGxsZCZM6fj5aUiPz+BtrZSbt8+ZBQjGMHAIQ1WHj9up6+vjUeP2vnmm/d17jJpsKP/+VC3e7RiqESIfokBO7vJuLk54Os7leBgta7UgJeXCi8vJ955ZwYrVsQYVQCREJuXRBKbgwcLSE+PIjNTy7FjJf18rPqic/XqftavX0RmppaKimxOndqqO0aIjUAwMjEkNvrF06RiafpF1JKSZpOZqWXjxlSam4vo6dnH48eGiy2OJITYvCTSyPLevfe4dKmG7u4aPv+8ud+PTf9HqO/++PLLY7q/CTeaQDAyMeRG0y8LLZWB1i8PLW20euVKLTdvNujKQw/1dQ0EQmxeEaIC58shisoJRhPG2F8IsXlFiM7y5TDGl08gMIQx9hdCbAQjAkNiY4wvpUBgjAixEYwInucLFzMegWB4I8RGMKIRMx6BYGQgxEYwohEzHoFgZCDERmCUiBmPQDC8EGIjMErEjEcgGF4IsRGMKsSMRyAYGoTYCEYVYsYjEAwNQmwErwRpW5/e3iPcvNmg2wdO+vyLL47y2WeN3L9/mG+/ffXbcwixEQgGFyE2gleCtBdcW9smduxYTm3tGu7cadR9fuJEGXv2rKapaT337x9+5e0TbjSBYHARYiN4JUjFo/buzWXlyhiKi1O4du2A7vPa2jWsXRtPWdlSbtyoH/L2CoYXopTCyEeIjeCVYEhUDInQULdXMLwQReJGPkJsXhLhfnkxJFHZv38t+fmJbNuWwaefCrEZ6eiX2DhzZjvHj2+mtbWU1tZSTp3axqVLNf3qO0ni8cEHOzlxoszg96U6MGfP7qC6OoeysqVUVq7g6NFibtyo58mT4/zwQ8eQ3wfB8xFi85KIheUX43liI9xoIxP94oEhIRo0GgUqlRyVSk5AgCvp6VG6NTrpOKl4YGSkNx4ejga/f+dOI7W1a8jI0BISokGttsfV1ZboaF/27s3l6tX9PHliHMXFjJ1RIzaDNQMRYvNiPM+NJsRmZPLgQTPNzUXk5MzHy0uFtfVE7OzMsbWdhJWVKQ4Ok5k+XUlKSjjHj2/ms88auXp1P/v3ryUszANbW3NsbCZiaWnCpEljsbY2w91dydKlc+joKKezcycrV8Ywe7Y7/v4uaDQKFAoL/Pymsn79Ik6d2sqXXx4b8vsgeD6jRmwGSxSEG+3FeF6AgHCjjUyuXKmloCCRsDAP3NwcCAycxtq18ZSXZ1JUlExCwkwcHCbj4mJDQUEie/asZv36RcTFheDkJMfV1Y709CgKC5PIyIgmMtILhUKGj48zFRXZ1NauYf78IObM8aa4OIUdOzJZtSqWrKy5rF+fxMGDBdy7996Q3wfB8zFasdEXATEDGRj082I+/bSeTz+t59atg9y928TDhy2/unD7PLHZs2f1jx3IIq5e3d/v+KdPT/PwYQt37zZx69ZBbt5s4PbtQ7qyuaNF9P/977M8fXqavr42bt8+xLVrB7hxo16Xn/SieUuG7uft24e4ebNB91wlDJ3nww8rmD8/kKlTbfD2VpGWFsmJE2XcvNlAV1c1W7akM3WqNXK5KfFxISxbFkVYmAcajQJHR0vCwz2pr19HV1c1bW2l5Ocn4ORkhaOjJatXL6CkZDFarR9arR8lJYspL89kxYp5ZGREU1goxGYkYbRioy8uo6UzGmz082K2bctg27YMKiqyqatbR0dHOQ8ftvQ77nlutOeJzcOHLXR0lFNXt46Kimx27FhOdfVK2tpK6e09MmoGE89E4hhdXdVUV6+kuDiFsrKluvykF81bMnQ/q6tXsmPHct1zlTB0nvff34KXlxOWlibMmxfAzp3LuXp1P48ft/PgwWEOH95AVJQPGo2CiIgZhIV56MQkONiN3Nw4LlyopK+vjd7eIzQ1FRIUpMbZ2ZqkpNnk5MwnOTkcrdaPoCA106bZYWVliru7koKCROFGG0EYrdhIIzwRrTIwfP/9Gfr62rh0qYbKyhXk5saRkaElNTWClJRwkpPDSE4OY/36RXzwwY5+M5zfG/osRSMdP76ZgoJEUlLCSU2NYPHid0hKmsWqVbHU16/j4sUq7t5tMtrnLc1o7txppKVlI1u2LCUzU0tychjLlkVTXJzC0aMlnDy5lbq6dWzevISsrLmUlqZx/Xpdv/Pdv3+YpqZCSkoWk5Mzn+XL32XVqlhWrYpl+fJ3WbYs+hdIAR3652ltLUWlkmNiMob4+FDq6tZx926TTvzPnNlOQkIo06cr8fZW4epqh4nJm9jaTmLhwln9Agc6O3cSHe2Li4stkZFepKdHsWFDMrm5cYSHe6JW2+PoKGP2bHd2784RAQIjCCE2gheir6+Nrq5qtm5dRkCAK87O1kREeBEfF8K8eQEEBamxtzfHw0PJ+vWL+s1wfm9SpxSNlJISjouLDQqFjPBwT91oWXLfSAvKxvq8pRlNS8tG5s8PxMfHmdjYIJYtiyYnZz7Z2fNYtCiM+PhQkpJmk5g4k5iYQPLyErh8ubbf+fTFJiNDy/Ll77J8+btkZGh/s9iMHfs3oqJ8qKjI5tatgzpPwtmzO3j3XT/s7SejUMiwsJjAX//6Z2xsJrJuXQKdnTv56quffifP3HJBuLjY4uc3lSVLImlp2ciFC5XU169j164sKitXcPjwBq5frzPa522MCLERvBCff97MsWMlrFgxj6lTrXF0tGTRojAKChLJzV2AVuuHqelbmJuPIzFxpm6EKx1vyF1mKCRaOu7SpRrS06PQaBTI5aa4uNiQkhJOVtZcIiO90GgU2NhMJDRUw5EjRfT1tfH992eG/H4NNI8ft9PTs5fNm5egUMiQyUxITY3Qub8KC5MID/fEzc0BNzcHfHyciYry0d1nfTeyvhtN3232om60U6e2ERDgyuTJ45kxw4n09CiOHi3h8uVaurtrqKpaiZeXChOTt5DJTDAxeZM//vG/sbIypagome7uGh49ated7/z5SuLiQnBxscXdXUlaWgQffbRbN8O9caOOO3caRVLnCESIjeCFuHu3ibq6PFavjiU2NkjXqVy5UktPzz6qqlbi5uaAXG5GTEygboQrHf97xUbqzORyU8LDPSkoSOT48c189NFuTpwoY8uWpbzzjicxMQEcOVKkCxgY6vs10Dx4cJjm5g2kpUVgbj4OhUJGdXWObmG/rW0TqakRuLk5YGr6Fra2k4iPD2HPntV89lljvzUt/QAB/YCAFw0QkAYDarU9kyeP1w1C8vISyMzUEhbmganpW7z22l+QyUwwNx/Pn/70BywsJrB69YJ+M2BDYiO1/+uvT/Cvf50U29WMQIxWbAZ7wXi0BRxIbpeiomQyM7WsWRNHQ0M+J09upb19M8XFKbi62mFtPZHoaN9+oiG54fbvX0tOzvx+bjR9sZEGCw0N+SiVMiZNGktGRnS/gIDu7hpKS1MpLk6hs3On0Y54b98+RHX1SubPD0Qmm4CHhyMnTpTp/t7Ts4/c3AV4eDjy5puvYW1txpo1cbrOXP99MJTBb4jz5yv55z9a+7VLcnMuWhSGo6MllpYm+PpOJTzck5AQjU78xo17A3v7yVhZmfLnP/8Rc/NxZGXN5cSJMr744qjufJLYqNX2+Pu7kJ09j48/3jPk91/w8hit2Ay2GIyW6CeJZ6JQwe7dOSxdOofISC9CQzX4+DijVttjYzORMWNew8JiAnPmePcTG8kN1NRUSH5+Yr8AAX2xkTrDzZuXYG1thqWlCYWFSXR1VdPX16Z7vo8etXP9eh3Xrh3gq69ajHbEe/NmAzt2LGfBgmBcXe2IjPTmgw926v4u5bsEBk7D3Hwc7u5KGhrydYEa+u+DoQx+Q8THhXD+fGW/dknuraNHS3Q7CHh7q3SCExbmgZeXExqNgunTldjbT+Yvf/nTc8XGw8OR6GhfkXdlRBit2DyPlxWj0SY20ppNYWES777rh5eXE25uDqhUchQKGZaWJowd+zeDM5vfKjaPHrXT3V1DUVEyVlamyOWmbNy4mJ6evTx+/JOP/9tvT3H//mHu3m3i0aN2oxWbTz+tZ9u2DGJiAn+M1Pp1sQkOdsPGZhLBwW6cPLnV4O/72UwojoAAVxQKCyZPHo9MNgGZzOQXWFqaIJebEh3tQ0dHeb/zSff/zJntbNqURnp6FAsXziI5OZycnPksWxZNWJgHvr5TCQ5Wo9EoGDfuDaysTElKms2BA3ncvn1Id14pGk2ttmf+/CCDgQmCkceoFZuXFYvR5kbr7q4hM1OLt7eKqVNt8PJyIjk5jMLCJLZvzyA3dwHe3iqDncRvdaN988373Lp1kPLyTGxtJ/Wb2UjnfebeW09d3Tq6u2uM1o0miU1kpDfm5uMMutECAlxxcLBg1ix32ts3Gfx99/Yeoa2tlPLyTPLyEli5Moa1a+PJz0/8BYWFSWzcuJi6ujyuX6/rdz7p/m/alEZBwbNBREvLRs6fr+T8+UqqqlYSFKRGpZITEeFFRIQXKpX1z/JsFnDhQqXuvKdObcXf38XgoEUwcjF6sRFlgAeGs2d3EB7uyeTJ47G0NCUoSM22bcs4eXILHR3b2bUri8DAabi42BITE/ibxUY/9FkK9d2/fy0qlRwLiwksXvwODQ35XL26X5ch39paqgvPbW0t5f799/j225NDdp8Gi88+a2TPntXExAQyfvwYHB0taWws1AXBdHSUk5Q0GxcXW+RyM/z8XNi5czmXLu3m3r33+gXKSO6v7u4aOjrKOXVqK52dO3UiIdHVVU1Pz17dtv7674vk3pNmNGvWxHHiRBmffLKX06e3UVSUjLOzNQ4OFixdOod16xKYPz8If38X1Gp75szxprZ2DV1d1Vy4UMnWrctQKp+FSC9cOKtfVKNg5GL0YmNIVEbbzORlOXNmOyEhGszM3sbGZhJarR+traVcvryPQ4ee7fhrYzMRc/NxREb+9jUb/fwbKYmxtbUULy8nzMzextNzCmlpkTQ05Osy5Jcti0alkuPtrWL//rVGKzZffHGUEyfKyMqai7n5OOzszNm1K4urV/dz9ep+9u3LxcfHmXHj3mDcuDdQKGTExAT+mOxZ3C/5UXovHj1q5+HDFr788hhffdXCP//R+gv6+tp4/PingmX674sUuLBw4SzUanvc3ZVkZc0lPz+RuLgQNBolY8a8xpQpluzenUNn504qK1ewaNFslEoZU6ZYsWRJJAUFiaSmRuDv78qbb76Ojc1EiotT+oVGC0Yuo1ZsBorRIlrSwq1SKcPW1pzAwGmUlS3VicSsWdN/XFsxIzzcs1/murQGc+jQ3/n73xe+cD2brq5qUlLCdQmcfn4upKVFsmJFDPHxobpk0uBgNU1NhUbrRpMCJiorVxD+fCm1AAAENElEQVQQ4IqnpyPr1iVw4MBa6uvXUVSUTHCwG1OmWOHqaoeHhyOBgdNISQmnvn7doGXaS+64NWvicHdX4uQkR6v1IzY2GB8fZ1QqaxQKGfPm+XPu3C7dDHf79gxdOYLY2CASE2cSGqpBo1EyZYolc+Z4ceRIkdE+z9GI0YuNiEobGJ6tGSwjOtoXa+uJjB8/Bjs7c5ycrFAqZTg7W+PpOYXgYDciIrz6Za5LSYS7d+eQl5fwwvVspPyS3NwFBAe7oVDIsLY2w8rKFBubSbi5OaDV+lJSsphPPtlrtAECUij4pUs1bN26TOe2SkgIJSUlnMxMLXl5CWzYkExxcQorV8YwZ443qanvcObM9kHLN/vuu1P09h7Rzbq0Wj/i4kKIjw8lNjaY1NQINm5M5dixEj7/vFm37ZEkOCtWzCMzU0taWiSJiTNZunQOpaWpHDlSxGefHTLa5zkaMXqxMcRAidBoERtJLMrKlhId7YtGo8DFxQa12h4fH2eio33Jzp6n21FAP6lTOn7v3lyKi1Oors7h9u1Duo7n0KG/U1qapvtcOk5aW2hrKyU3N04Xqiv937i4ELZtW2ZwA1BjQ7pfdXXryMtLID09iuzseZSWPuvQpbWW5uYi3YL9q6gPJAUKlJUtpbg4RbdBqKHADek6mpuLqK7O0e1UYOyBHqOFX+tfR63YDJRIjBY3mpRxfuNGPZ2dOzl+fDNtbZtob9/MyZPPFpc//niPbkeBW7cO8s037+uOl9xoLS0b2bs3l+bmIh48aNat5bS3b2Lfvp8+139Ovb1H6OnZp0tClP7v+fOVfPppvcHSBsaGNDO4e7eJy5druXSpho8/3sP163V8/nmzbq3lwYNmrlyp5caNer7++sSgt0sKgb5xo55r1w7oSh8YCkmXruPBg2Zu3z6k26nA2EPYRwu/1r8KsTHyGclwQT/6SQphNvT5ULf3VTNaBi2C0YEQm58hXu5Xi370k7RhpqHPh7q9Q3V/xOBHYAwIN5pg0BEi/vsQYiMwdoTYCAYU0Wn+PoRIC4wdITaCAUWIzeAiREkwUhFiIxhQRGc4uAgxF4xUhNgIBCMIsf2SYKQixEYgGEGIjWUFIxUhNoJXghh5Dy5CbATDHSE2gleC6AwHFyHmguGOEBvBK0FfbETnKBCMLoTYCF4J+uIiZjoCwehCiI1gSBAzHYFgdCHERjAkiJmOQDC6EGIjGBaImY5AYNwIsREMC8RMRyAwboTYCIYlkth88837PH16WsxwBIIRjhAbwbBEmt08fXqab755X8xwBIIRjhAbwbDmhx86ePLkOE+eHOeHHzqGvD0CgeD38V8IEyZMmDBhg2xCbIQJEyZM2KCbEBthwoQJEzboJsRGmDBhwoQNugmxESZMmDBhg25CbIQJEyZM2KCbEBthwoQJEzboJsRGmDBhwoQNuv0/bLLDEMWwoPYAAAAASUVORK5CYII=[/img]
Schreibe die Überschrift in dein Schulübungsheft. Zeichne die drei Trapeze in deinem Heft und beschrifte sie, wie im Bild. (Die Kästchen helfen dir beim Zeichnen)
[size=150][u][size=200]Flächeninhalt[/size][/u][/size]
1) Mit den schwarzen Schiebereglern veränderst du die größe des Trapezes. [br]2) Nutze den roten Schieberegler, um das Trapez zu drehen. [br][br]
Wie heißt die entstandene Figur?
Wie lautet die Formel für dei Berechnung des Flächeninhalts eines Rechtecks mit der Länge a cm und der Breite b cm ?
Wir noch einmal einen Blick auf das eben konstruierte Rechteck. [br][br]1) Welche Buchstaben bezeichnen die Länge und welche die Breite dieses Rechtecks ? [br]2) Wie muss diese Formel verändert werden, damit man die Flächeninhaltsformel für das ursprüngliche Trapez zu erhalten ? [br][br]