[b][color=#0000ff]UNA PREMESSA: FACCIAMO IL PUNTO SUGLI STRUMENTI[code][/code][/color][/b][code][br][/code]Per lavorare in questa pagina avrai bisogno di costruire funzioni, ed in particolari funzioni definite a tratti. A questo scopo Geogebra mette a disposizione due istruzioni:[br][br][list][*][color=#38761d][b]VERSIONE 1:[/b][/color] Se(Condizione, Allora)[br][br][/*][*][b][color=#0000ff][/color][color=#bf9000]VERSIONE 2:[/color][color=#0000ff] [/color][/b]Se(Condizione, Allora, Altrimenti)[br][br][/*][/list][b][color=#38761d]La prima versione[/color][/b] controlla [code]Condizione: [/code]quando è vera restituisce [code]Allora[/code][code][/code], altrimenti [u]non dà nessun risultato[/u] - quindi [color=#ff0000]quando [/color]la [code]Condizione[/code][code][/code] è falsa [color=#ff0000]il risultato della funzione [/color][color=#ff0000]non è definito[/color].[br][br]Ad esempio se scriviamo[br][br][code]y = Se(-2<x<3, 4+2x)[/code][br][br]otteniamo una funzione che SE x è compresa tra -2 e 3 restituisce 4+2x, altrimenti non è definita - la funzione non esiste fuori da questo intervallo. In termini matematici equivale ad una funzione definita a tratti... con un solo tratto![br][br][math]\large{ y=2x+4 \qquad \{-2\lt x \lt 3\} }[/math][br][br]La funzione è riprodotta nell'animazione qui sotto.[br][br]

[b][color=#b45f06]la seconda versione[/color][/b] di questo comando ci permette di costruire situazioni più articolate: se [code]Condizione[/code] è vera restituisce [code]Allora[/code], quando invece [code]Condizione[/code] è falsa il risultato è [code]Altrimenti[/code]. Ad esempio se dobbiamo riprodurre la funzione definita a tratti[br][br][math]\large{y=\begin{cases}x+3&\qquad x\lt2\\5-x&\qquad x\ge2 \end{cases}}[/math][br]potremmo provare a scrivere [br][br][code]y=se(x<2, x+3, 5-x)[/code][br][br]Vedi il risultato qui sotto

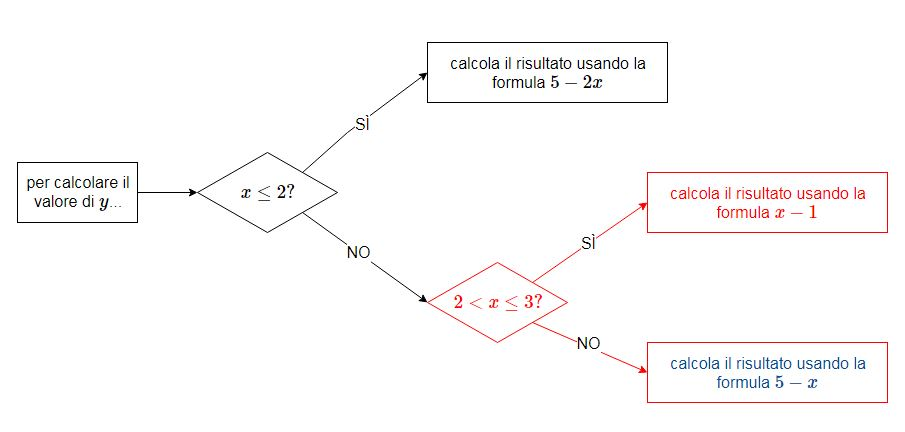
Per ottenere risultati ancora più articolati è possibile [b][color=#b45f06]innestare una dentro l'altra più funzioni del secondo tipo[/color][/b]. Ad esempio per ottenere[br][br][math]\large{y=\begin{cases}5-2x&\qquad x\le 2 \\ x-1&\qquad 2\lt x\le 3\\5-x&\qquad x\gt3\end{cases}}[/math][br][br]Possiamo utilizzare una combinazione del tipo[br][br][math]\large{\mbox{Se}(x\lt=2\ ,\ 5-2x,\ \textcolor{red}{\mbox{Se}(2\lt x \lt = 3,\ x-1,\ \textcolor{blue}{5-x})})}[/math] [br][br]La [math]\large{y}[/math] viene calcolata in questo modo: se [math]\large{x\le 2}[/math] (primo intervallo), verrà utilizzata l'espressione [math]\large{5-2x}[/math] [color=#ff0000]altrimenti fa un ulteriore controllo: se è vera [math]\large{\textcolor{red}{2\lt x\le 3}}[/math] (secondo intervallo) calcoleremo la [math]\large{\textcolor{red}{y}}[/math] tramite l'espressione[/color] [math]\large{\textcolor{red}{x-1}}[/math], [color=#0000ff]altrimenti (terzo intervallo) useremo la formula[/color] [math]\large{\textcolor{blue}{5-x}}[/math].[br]

[color=#ff0000][b]Quando si utilizza una tecnica di questo tipo è importante controllare che le funzioni siano innestate correttamente: ogni nuovo Se svolge il ruolo dell'Altrimenti per il Se precedente; inoltre ogni parentesi che viene aperta deve essere chiusa nel punto opportuno[/b][/color].[br][br]Qui sotto vedi la funzione; come al solito puoi cliccare sulla sua espressione per verificare come è fatta.

Si può innestare un numero qualsiasi di controlli uno dentro l'altro, ottenendo così funzioni costituite da un qualsiasi numero di tratti. [br][b][br][color=#38761d]Per vedere alcuni esempi di funzioni costruite in questo modo fa riferimento all'applet qui sotto, che puoi cliccare ed ispezionare a piacere[/color][/b].

[size=150][color=#ff0000]LE FUNZIONI COME LEGAME TRA UN INPUT ED UN OUTPUT[/color][/size][br]Abbiamo definito una [b][color=#ff0000]funzione[/color][/b] come un particolare tipo di [color=#ff0000][b]connessione tra due insiemi, che per ogni elemento di partenza, o [i]input,[/i] restituisce un risultato, o [i]output[/i][/b][/color]. Una delle applicazioni più frequenti di questo tipo di strumento è la possibilità di stabilire la [i]legge[/i] con cui definiamo come deve comportarsi un certo elemento.[br][br]Vediamo un semplice esempio.[br][br]Supponiamo di avere una macchina in cui c'è un disco verde. Noi vogliamo che una volta che la macchina sia accesa il disco sia[br][list][*]in una certa posizione [b][color=#0000ff]per i primi due secondi[/color][/b], ad esempio nel punto [math]\large{\textcolor{blue}{(-1,4)}}[/math] in un certo sistema di riferimento[/*][*]in un'altra posizione [b][color=#38761d]per i tre secondi successivi[/color][/b], ad esempio nel punto [math]\large{\textcolor{#ff7700}{(-1,0)}}[/math][br][/*][/list][br][ipotizziamo che dopo cinque secondi il ciclo ricominci]. [br][br]L'animazione sotto usa una funzione per impostare questo comportamento:[br][list][*]la variabile [math]\large{\textcolor{red}{t}}[/math], libera di cambiare da 0 a 5, simula il tempo che passa - e quando attiveremo l'animazione [premendo sulla freccia nell'angolo in basso a sinistra del piano cartesiano] SARÀ il tempo che passa.[/*][*]la funzione [math]\large{\textcolor{#007700}{f}}[/math], definita a tratti, restituisce come risultato [math]\large{\textcolor{blue}{4}}[/math] quando l'input è minore o uguale di 2, e [math]\large{\textcolor{#ff7700}{0}}[/math] quando l'input è compreso tra 2 e 5. Proprio come serve a noi![/*][/list][br][b]A questo punto è fatta![/b] Usiamo la variabile [math]\large{ \textcolor{red}{t}}[/math] come input della funzione [math]\large{\textcolor{#007700}{f}}[/math] e prendiamo [math]\large{\textcolor{#007700}{f(t)}}[/math], il risultato che ci restituisce la funzione (e che abbiamo modellato come vogliamo noi), per usarlo come coordinata [math]\large{y}[/math] del nostro disco verde.[br][br][center][math]\Large{ \textcolor{red}{t} \underrightarrow{\text{\small{\ dato t, f restituisce\ \ }}} \textcolor{#007700}{f(t)} \underrightarrow{\text{\small{\ il risultato f(t) è usato da \ \ }}} A(0,\textcolor{#007700}{f(t)}) }[/math][/center][br][br]Nota: Geogebra permette di [b]animare[/b] gli slider, facendo cambiare automaticamente la posizione del cursore e quindi il valore della variabile. Questa opzione ci sarà utile per definire funzioni il cui output deve cambiare in funzione del [b]tempo[/b].

Sia la coordinata [math]\large{x}[/math] che la coordinata [math]\large{y}[/math] del punto dipenderanno dal parametro [math]\large{a}[/math]. Definisci l'espressione di [math]\large{a}[/math] che, dato un certo valore di questo parametro, permette di calcolare la corrispondente coordinata [math]\large{x}[/math] del punto [math]\large{A}[/math]. Dovrebbe essere abbastanza semplice. Poi definisci l'espressione che calcola la coordinata [math]\large{y}[/math] del punto in funzione del valore di [math]\large{a}[/math]. Costruisci un punto le cui coordinate sono date da queste due espressioni... ed il gioco è fatto!

[b]NOTA:[/b] se necessario quando lo slider del tempo è visibile puoi anche trascinarlo manualmente per verificare accuratamente le caratteristiche del modo del punto secondo per secondo.

Generalizziamo ora il concetto. Vogliamo costruire un punto che percorra in continuazione il rettangolo riportato nell'animazione qui sotto, partendo da puunto A e muovendosi in senso antiorario.[br][br]Supponiamo che il punto si muova alla velocità di 1 quadretto al secondo. [br][br][list][*]costruisci uno slider t la cui estensione sia pari al tempo necessario al punto per compiere un intero giro. Nelle opzioni dello slider (accessibili con il tasto destro) specifica che dovrà muoversi in modo crescente. [/*][*]definisci la funzione a(t) che restituisca, dato un qualsiasi istante t, il valore che dovrà avere la coordinata x del punto[/*][*]definisci la funzione b(t) che restituisca, dato un qualsiasi istante t, il valore che dovrà avere la coordinata y del punto[/*][/list][br]A questo punto costruisci il punto usando le funzioni a(t) e b(t).[br]

[b][color=#ff0000]UNA VARIANTE IMPEGNATIVA[/color][/b][br]Ecco una sfida per toccare con mano quanto il concetto di funzione può rendere flessibile ogni tua creazione. Crea uno slider [b]v[/b] che vada da 1 a 4: indicherà la velocità del punto (1= un quadretto al secondo, 4=quattro quadretti al secondo). [br][br]Come devi modificare le tue funzioni in modo che cambiando il valore di v il punto si muova di conseguenza? [br][br]Per aiutarti disegna il grafico della tua funzione a(t) che calcola la x al variare del tempo. Come cambia il grafico se ad esempio il punto non si muove più con v=1 ma con v=2? E se v=4? Quindi per un v generico...

[b][color=#ff0000]UNA POSSIBILE VARIANTE[/color][/b]: il semaforo ha tre colori, lo sappiamo tutti. Crea un tuo semaforo che resta rosso 5 secondi, diventa giallo per 2 secondi poi verde per i successivi 8 secondi. Ovviamente ogni luce deve essere nella corretta posizione.