Medidas de Areas y Volumenes Ejercicios 9.1
Ejercicios Areas y volumenes Prismas
Table of Contents
- Ejercicio 15
- PROCEDIMIENTO
- ejercicio 25
- PROCEDIMIENTO
- ejercicio 33
- PROCEDIMIENTO
- ejercicio 38
- PROCEDIMIENTO
- ejercicio 42
- PROCEDIMIENTO
- ejercicio 44
- PROCEDIMIENTO
PROCEDIMIENTO
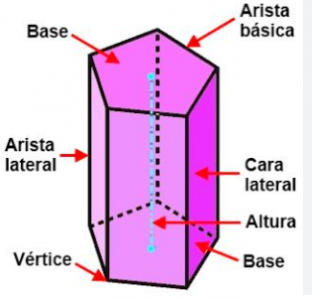
[b]En el prisma pentagonal regular mostrado suponga que cada arista de la base mide 9.2 cm y que la apotema de la base mide 6.3 cm. La altura del prisma mide 14.6 cm.[br][/b][br]a) Encuentre el área lateral del prisma.[br][br]b) Encuentre el área total del prisma.[br][br]c) Encuentre el volumen del prisma.
PASOS A SEGUIR
[color=#ff0000]1. Analizamos y establecemos los datos dados del problema [/color][br] Datos [br]Arista de la base: 9.2 cm [br]Apotema: 6.3 cm [br]Altura prisma: 14.6 cm [br] [br][color=#ff0000]2. El área lateral es igual al perímetro de la base (la suma de las medidas de los 5 lados del pentágono) por la altura del prisma o arista lateral[/color][br][br]a) Encuentre el área lateral del prisma.[br][br][math]A_{_{_L}}=P\times h[/math][br][math]A_{_{_L}}=9.2cm\left(5\right)\times14.6cm[/math][br][math]A_{_{_L}}=46cm\times14,6cm[/math][br][math]A_{_{_L}}=671.6cm^2[/math][br][br][color=#ff0000]3. El área total de un prisma es igual a la suma de su área lateral (área de sus caras laterales) y el área de sus dos bases.[/color][br]El área de la base es igual al perímetro por el apotema dividido entre dos[br][br][math]A_B=\frac{P\times a}{2}[/math][br][math]A_B=\frac{46cm\times6.3cm}{2}[/math][br][math]A_B=144.9cm^2[/math][br][br]b) Encuentre el área total del prisma.[br][br][math]A_T=A_L+2A_B[/math][br][math]A_T=671.6cm^2+2\left(144.9cm2\right)[/math][br][math]A_T=671.6cm^2+289.8cm^2[/math][br][math]A_T=961.4cm^2[/math][br][br][color=#ff0000]4. La fórmula para calcular el volumen de cualquier prisma recto es la misma: V = área de la base por altura[/color][br][br]c) Encuentre el volumen del prisma.[br][br][math]V=A_B\times h[/math][br][math]V=144.9cm^2\times14.6cm[/math][br][math]V=2115.54cm^3[/math][br][br]
PROCEDIMIENTO
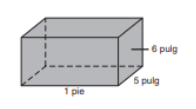
[b]La caja de las dimensiones indicadas va a ser construida con materiales que cuestan 1 centavo por pulgada cuadrada para la superficie lateral y dos centavos por pulgada cuadrada para las bases ¿Cual es el costo total de fabricar la caja?[br][/b]
PASOS A SEGUIR [br][br]DATOS [br]h= 6 pulg[br]a= 5 pulg[br]b= 1pie convertido a pulg es igual 12 pulgadas[br][br][color=#ff0000]1. Calculamos el area lateral [/color][br]AL= Pb x h [br]AL=(12pulg+12pulg+5pulg+5pulg) x 6pulg[br]AL= 204 [math]pulg^2[/math][br][br][color=#ff0000]2. Calculamos el area de las dos bases [/color][br]Ab= b x a[br]Ab= 12 pulg x 5 pulg[br]Ab= 60 [math]pulg^2[/math][br][br][color=#ff0000]3. Realizamos la correspondiente asignacion de costos por pulgada [/color][br][br]Area lateral - 1 centavo por pulgada [br][br]AL= 204 [math]pulg^2[/math]x 1 ctv[br]AL= 204 ctvs[br][br]Area base - 2 centavos por pulgad[br][br]Ab= 60 [math]pulg^2[/math]x 2 ctvs[br]Ab= 120 ctvs[br][br][color=#ff0000]4. Sumamos los dos valores ya correspondientes [/color][br][br]AL + Ab [br]204 ctvs + 120 ctvs[br]324 ctvs [br][color=#980000][br]El costo total para fabricar la caja es de 324 centavos. Esto tambien quiere decir que es un total de $3,24 [br] [/color][br]
PROCEDIMIENTO
Una diagonal de un cubo une dos vértices de manera que los puntos restantes de la diagonal se encuentran en el interior del cubo. Demuestre que la diagonal del cubo que tiene aristas de longitud e es de 1 3 unidades de largo.
Un cubo es en hexaedro regular con 8 vértices,12 aristas y 6 caras cuadradas idénticas. Una diagonal del cubo es una línea que une dos vértices opuestos a través del interior del cubo [br]Una diagonal del cubo conecta dos vértices opuestos. Si los vértices son (0,0,0)(0,0,0)y (a,a,a)y (ą,ą,ą), entonces la longitud de la diagonal se puede calcular utilizando la distancia Euclidiada tridimensional [br][math]d=\sqrt{\left(a-0^2\right)+\left(a-0\right)^2+\left(a-0\right)^2}[/math][br][br][math]d=\sqrt{a^2+a^2+a^2}[/math][br][br][math]d=\sqrt{3a^2}[/math][br][br][math]d=a\sqrt{3}[/math][br][br]Encontramos el valor de a para la diagonal 13:[br][br][math]a=\frac{13}{\sqrt{3}}[/math][br][br][math]a=\frac{13\sqrt{3}}{3}[/math][br][br][math]13=a\sqrt{3}[/math][br][br]Respuesta: La longitud de la diagonal del cubo de aristas de [math]a=\sqrt{3}[/math] es 13.
PROCEDIMIENTO
Repita el ejercicio 35 (para encontrar el volumen), pero con los cuatro cuadrados congruentes con lados de 6 pulg de longitud que se cortan de las esquinas de una pieza rectangular de cartulina que mide 20 pulg de ancho y 30 pulg de largo.
DATOS:[br][br]Lados: 6 pulgadas[br]Cartulina: 20 pulgadas de ancho y 30 pulgadas de largo.[br][br] 1. Cortar los cuadrados: Ancho actual: 20-2*6=8 pulgadas[br] Largo actual: 30-2*6=18 pulgadas[br][br] 2. Doblar las solapas:[br] Altura de la caja=6 pulgadas[br][br] 3. Calcular el volumen:[br] [math]V=a\ast l\ast h[/math][br] [math]V=8\ast18\ast6[/math][br] [math]V=864in^3[/math][br][br]Respuesta: El volumen de la caja es de [math]864in^3[/math]
PROCEDIMIENTO
[b]Para los ejercicios 41-43 considere el prisma pentagonal regular oblicuo que se muestra. Cada lado de la base mide 12 cm y la altura mide 12 cm.[br][br] 42. Encuentre el área total del prisma. [/b]
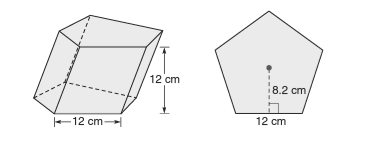
[color=#ff0000]1. Analizamos y establecemos los datos dados en el problema [/color][br]Datos [br]Base: 12 cm [br]Altura: 12 cm [br]Apotema: 8.2 cm [br][br][color=#ff0000]2. Primeramente, debemos encontrar el área lateral de un prisma pentagonal regular oblicuo, es igual al perímetro por la altura. [/color][br][br]a) Encuentre el área lateral del prisma.[br][br][math]A_{_{_L}}=P\times h[/math][br][math]A_{_{_L}}=12cm\left(5\right)\times12cm[/math][br][math]A_{_{_L}}=60cm\times12cm[/math][br][math]A_{_{_L}}=720cm^2[/math][br][br][color=#ff0000]3. El área total de un prisma es igual a la suma de su área lateral (área de sus caras laterales) y el área de sus dos bases.[/color][br]El área de la base es igual al perímetro por el apotema dividido entre dos[br][br][math]A_B=\frac{P\times a}{2}[/math][br][math]A_B=\frac{60cm\times8.2cm}{2}[/math][br][math]A_B=246cm^2[/math][br][br][b]42) Encuentre el área total del prisma.[/b][br][br][math]A_T=A_L+2A_B[/math][br][math]A_T=720cm^2+2\left(246cm^2\right)[/math][br][math]A_T=720cm^2+492cm^2[/math][br][math]A_T=1212cm^2[/math][br][br]
PROCEDIMIENTO
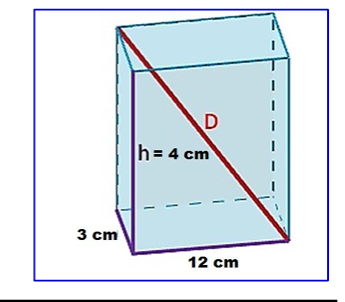
Se puede demostrar que la longitud de una diagonal de un prisma rectangular recto con dimensiones [math]\ell[/math] , w y h está dada por [math]d=\sqrt{\ell^2+w^2+h^2}[/math]. Utilice esta fórmula para encontrar la longitud de la diagonal cuando [math]\ell[/math] = 12 pulg, w = 4 pulg y h = 3 pulg.
PASOS A SEGUIR [br][br][color=#ff0000]1. Analizamos los datos correspondientes [br][/color]DATOS [br] [math]\ell[/math] = 12 pulg[br] w = 4 pulg [br] h = 3 pulg.[br][color=#ff0000][br]2. Aplicamos la formula dada [/color][br][math]d=\sqrt{\ell^2+w^2+h^2}[/math][br][br][color=#ff0000]3. Reemplazamos los valores [/color][br][br][math]d=\sqrt{\left(12\right)^2+\left(4\right)^2+\left(3\right)^2}[/math][br][br][color=#ff0000]4. Resolvemos la operacion [/color][br][br][math]d=\sqrt{144+14+9}[/math][br][br][color=#ff0000]5.Resolvemos la suma y luego la raiz y asi obtenemos nuestro resultado [br][math]d=\sqrt{169}[/math][br][/color][math]d=13pulg[/math]
