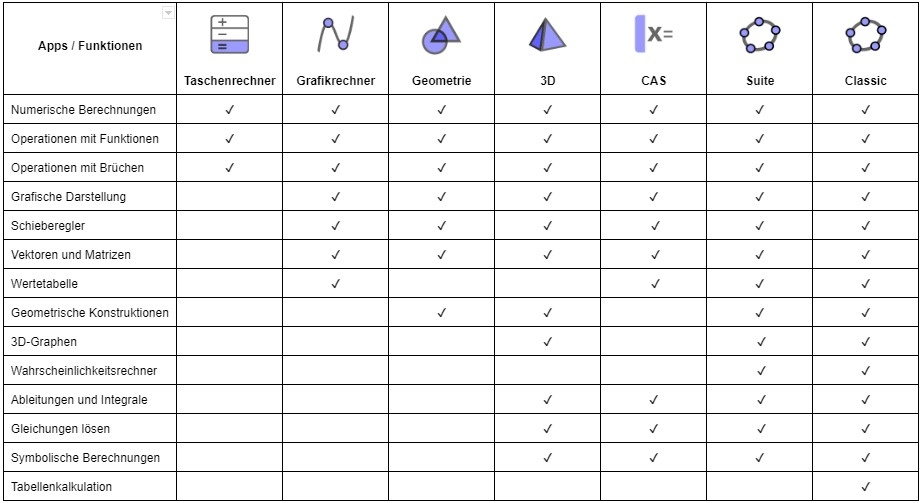
Vergleich der GeoGebra Mathe Apps
Mit unseren [i]GeoGebra Mathe Apps[/i] kannst du Funktionen, Geometrie, Algebra, Statistik und 3D auf eine neue und interaktive Weise erkunden und lernen.[br][list][*][url=http://www.geogebra.org/scientific]Taschenrechner[/url][br][/*][*][url=https://www.geogebra.org/graphing]Grafikrechner[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometrie[/url][br][/*][*][url=https://www.geogebra.org/calculator]Rechner Suite[/url][/*][*][url=https://www.geogebra.org/cas]CAS Rechner[/url][br][/*][*][url=https://www.geogebra.org/3d]3D Rechner[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Classic[/url][br][/*][/list]Die richtige App für dich ist die, die deinen eigenen Bedürfnissen entspricht und, wenn sie in Prüfungen verwendet wird, die Prüfungsbestimmungen für deine Region erfüllt. Die folgende Tabelle gibt einen Überblick darüber, welche Funktionen in welchen Apps verfügbar sind.

GeoGebra in Prüfungen
Wir glauben, dass die Schüler*innen davon profitieren, wenn sie im Unterricht, bei den Hausübungen und während Prüfungen genau dieselbe [i]GeoGebra [/i]App verwenden. Auf diese Weise erhalten sie die meiste Übung mit der App und können unsere Technologie daher in allen Situationen optimal nutzen. Aus diesem Grund haben wir unseren [i]GeoGebra Prüfungsmodus[/i] erstellt und ihn in jede unserer Apps eingefügt. Der [i]Prüfungsmodus [/i]sperrt mobile Geräte, sodass die Schüler*innen während einer Prüfung keine anderen Apps als [i]GeoGebra[/i] verwenden und mit diesen kommunizieren können. Dieser Ansatz wurde bereits von mehreren Bildungsministerien in mehreren Regionen erprobt und genehmigt. Erfahre mehr über die Verwendung von [url=https://www.geogebra.org/m/m97r7cd4][i]GeoGebra[/i] in Prüfungen[/url].[br][br]
Parallelogramm
Aufgabe
Konstruiere ein Parallelogramm und verändere es, indem du an den Eckpunkten der Figur ziehst. Erforsche, wie sich die Werte der Längen und Winkel dadurch verändern. [br][br]Erforsche die folgende Konstruktion und lerne, wie du die Eigenschaften eines Parallelogramms mit [url=https://www.geogebra.org/geometry]GeoGebra Geometrie[/url] erforschen kannst. Danach versuche es selbst, indem du die folgenden Anleitungen befolgst.
Erforsche die Konstruktion...
Anleitungen
[b]Anmerkung:[/b] Falls du die Mobile-App verwendest, gehe sicher, dass die [i]Objektname anzeigen [/i]Option auf [i]Nur neue Punkte[/i] gestellt ist. Du kannst dies in den [i]Einstellungen [/i]des App-Menüs unter [i]Allgemein[/i] ändern. [br][table][tr][td]1.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_join.png[/icon][/td][td]Wähle das [i]Gerade[/i] Werkzeug und erstelle eine Gerade [i]AB[/i], indem du zweimal in die [i]Grafik-Ansicht[/i] klickst.[/td][/tr][tr][td]2.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_join.png[/icon][/td][td]Erstelle eine Gerade [i]BC[/i], indem du erneut das [i]Gerade[/i] Werkzeug verwendest.[br][b]Hinweis:[/b] Wähle den Punkt [i]B[/i] aus und klicke dann in die [i]Grafik-Ansicht[/i], um den Punkt [i]C [/i]zu erstellen.[/td][/tr][tr][td]3.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_parallel.png[/icon][/td][td]Aktivierte das [i]Parallele Gerade [/i]Werkzeug und erstelle eine parallele Gerade zur Gerade [i]AB[/i] durch den Punkt [i]C[/i]. [br][b]Hinweis:[/b] Wähle zuerst die Gerade [i]AB[/i] und dann den Punkt [i]C[/i] aus.[/td][/tr][tr][td]4.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_parallel.png[/icon][/td][td]Erstelle, erneut mit Hilfe des [i]Parallele Gerade[/i] Werkzeugs, eine parallele Gerade zur Gerade [i]BC[/i] durch den Punkt [i]A[/i]. [/td][/tr][tr][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_intersect.png[/icon][/td][td]Wähle das [i]Schnittpunkt [/i]Werkzeug aus und konstruiere den Schnittpunkt [i]D[/i] der beiden Geraden. [br][b]Hinweis:[/b] Klicke direkt auf den Schnittpunkt.[/td][/tr][tr][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_polygon.png[/icon][/td][td]Aktiviere das [i]Vieleck[/i] Werkzeug und erzeuge ein Parallelogramm [i]ABCD[/i], indem du nacheinander die Eckpunkte auswählst.[br][b]Hinweis:[/b] Um das Vieleck zu schließen, wähle den ersten Punkt erneut aus.[/td][/tr][tr][td]7.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_showhideobject.png[/icon][/td][td]Wähle das [i]Objekt anzeigen / ausblenden [/i]Werkzeug und blende alle Hilfsgeraden aus, indem du die Geraden anklickst.[br][/td][/tr][tr][td]8.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_showhidelabel.png[/icon][/td][td]Wähle ein Segment aus, indem du das [i]Bewege[/i] Werkzeug verwendest und wähle [i]Beschriftung anzeigen [/i]aus. Wiederhole diesen Schritt für alle Seiten des Parallelogramms. [br][b]Anmerkung:[/b] In der Mobile-App aktiviere den [i]Mehr[/i]-Button und wähle anschließend unter [i]Beschriftungsstil Wert [/i]aus.[/td][/tr][tr][td]9.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_angle.png[/icon][/td][td]Zeige die Werte der Winkel an, indem du das [i]Winkel [/i]Werkzeug und dann das Parallelogramm auswählst. [/td][/tr][tr][td]10.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Wähle das [i]Bewege[/i] Werkzeug aus und erforsche die Eigenschaften deiner Konstruktion. [/td][/tr][/table]
Versuche es selbst...
Anleitungen (fortgesetzt)
[table][tr][td]11.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_segment.png[/icon][/td][td]Konstruiere die Diagonalen des Parallelogramms mit dem [i]Strecken [/i]Werkzeug. Für die erste Diagonale wähle den Punkt [i]A[/i] und dann den Punkt [i]C[/i], für die zweite Diagonale den Punkt [i]B[/i] und anschließend Punkt [i]D[/i] aus.[/td][/tr][tr][td]12.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_intersect.png[/icon][/td][td]Erzeuge den Schnittpunkt der Diagonalen mit dem [i]Schnittpunkt [/i]Werkzeug. [/td][/tr][tr][td]13.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_distance.png[/icon][/td][td]Aktiviere das [i]Abstand oder Länge [/i]Werkzeug und wähle jeweils einen Eckpunkt [i]A[/i], [i]B[/i], [i]C[/i], [i]D[/i] des Parallelogramms und den Schnittpunkt [i]E[/i] der Diagonalen aus. [br][b]Hinweis:[/b][i] [/i]Wähle Punkt [i]A [/i]und dann Punkt [i]E [/i]aus. Wiederhole dies mit den Punkten [i]B[/i], [i]C[/i] und [i]D[/i].[/td][/tr][tr][td]14.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_slope.png[/icon][/td][td]Aktiviere das [i]Steigung[/i] Werkzeug und wähle alle vier Seiten des Parallelogramms aus.[/td][/tr][tr][td]15.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Erforsche deine Konstruktion mit Hilfe des [i]Bewege [/i]Werkzeugs.[/td][/tr][/table]
Das Konzept der Kongruenz
Aufgabe
Erstelle zwei Dreiecke und überprüfe, ob die beiden Figuren kongruent sind oder nicht. [br][br]Erforsche die folgende Konstruktion und entdecke, wie du mit [url=https://www.geogebra.org/geometry]GeoGebra Geometrie[/url] überprüfen kannst, ob zwei Figuren kongruent sind oder nicht. Danach versuche es selbst, indem du die folgenden Anleitungen befolgst.
Erforsche die Konstruktion...
Anleitungen
[table][tr][td]1.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/f/f1/Stylingbar_graphicsview_show_or_hide_the_grid.svg/32px-Stylingbar_graphicsview_show_or_hide_the_grid.svg.png[/img][/td][td]Öffne die [img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/16px-Ic_settings_black.svg.png[/img] [i]Einstellungen,[/i] aktiviere [i]Koordinatengitter anzeigen[/i] und wähle [i]Enges Gitter.[br][/i][b]Anmerkung:[/b] In der Mobile-App wähle [i]Koordinatengitter anzeigen [/i]bevor du bei [i]Art des Koordinatengitters Enges Gitter [/i]auswählst.[i] [/i][/td][/tr][tr][td]2.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_polygon.png[/icon][/td][td]Erstelle zwei Dreiecke nebeneinander.[/td][/tr][tr][td]3.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Verwende das [i]Bewege [/i]Werkzeug, um einen Eckpunkt auszuwählen und dessen Stil zu ändern.[/td][/tr][tr][td]4.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_copyvisualstyle.png[/icon][/td][td]Verwende das [i]Übertrage Format [/i]Werkzeug, indem du den zuerst veränderten Eckpunkt auswählst und anschließend den gleichen Stil auf die anderen Punkte überträgst, indem du diese anklickst. [br][b]Hinweis:[/b] Wähle das [i]Bewege [/i]Werkzeug, um diese Option wieder zu verlassen.[/td][/tr][tr][td][i][/i]5.[/td][td][/td][td]Wechsle zur [i]Algebra-Ansicht.[/i][br]Tippe [math]Wenn[/math]([math]SindKongruent\left(d1,d2\right)[/math], [i]"kongruent", "nicht kongruent"[/i]) in das Eingabefeld und überprüfe, ob die Dreiecke kongruent sind. Falls sie kongruent sind, wird der gezeigte Text [i]kongruent [/i]lauten.[/td][/tr][tr][td]6.[/td][td][/td][td]Wechsle zurück zur [i]Werkzeug-Ansicht.[/i][/td][/tr][tr][td]7.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Verändere den Stil des Textes.[br][/td][/tr][tr][td]8.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Bewege die Ecken der Dreiecke, um zwei kongruente Dreiecke zu erhalten.[/td][/tr][/table][br][b]Anmerkung: [/b]Falls du die Online-App oder Desktop-App verwendest, kannst du alternativ statt den Schritten 6, 7 und 8 folgende Schritte befolgen: [br]Erstelle zuerst den booleschen Wert [i]kongruent[/i] mit dem Befehl [math]SindKongruent[/math]. Tippe dazu [math]kongruent=SindKongruent\left(d1,d2\right)[/math] in das [i]Eingabefeld.[br][/i]Wechsle danach zurück in die [i]Werkzeug-Ansicht [/i]und erstelle einen Text. Wähle im Dialogfeld [i]Erweitert [/i]und anschließend[i] [img]https://wiki.geogebra.org/uploads/thumb/4/4e/Geogebra-logo-elipse.svg/16px-Geogebra-logo-elipse.svg.png[/img] GeoGebra [/i]und wähle die Variable [i]kongruent [/i]aus. Um zu bestätigen, drücke [i]OK.[/i]
