[i][size=85][color=#e06666]Mari awali belajar dengan doa dan shalawat[/color][/size][/i]

Hal-hal yang diperlukan untuk membuat sketsa grafik fungsi kuadrat [math]f\left(x\right)=ax^2+bx+c[/math] adalah sebagai berikut:[br][b]1. Titik potong terhadap sumbu Y[/b][br] Grafik memotong sumbu Y jika [math]x=0[/math]. [br] [math]y=a\left(0\right)^2+b\left(0\right)+c[/math][br] [math]y=c[/math][br] [math]\therefore[/math]Titik potong terhadap sumbu Y = [math]\left(0,c\right)[/math][br][b]2. Titik potong terhadap sumbu X[/b][br] Grafik memotong sumbu X jika [math]y=0[/math][br] Dengan menggunakan rumus abc atau pemfaktoran, maka didapat [math]x_1[/math] dan [math]x_2[/math][br] [math]\therefore[/math]Titik potong terhadap sumbu X = [math]\left(x_1,0\right)[/math] dan [math]\left(x_2,0\right)[/math][br][b]3. Menentukan koordinat titik balik / titik puncak[/b][br] Tentukan [b]sumbu simetri[/b] [math]\left(x_p\right)[/math][math]=-\frac{b}{2a}[/math][br] Kemudian tentukan [b]ordinat titik puncak [math]y_p=-\frac{D}{4a}[/math] [/b]atau [math]y_p=f\left(x_p\right)[/math][br] Dimana [b]diskriminan [/b][math]D=b^2-4ac[/math][br] [math]\therefore[/math]Titik balik grafik [math]=\left(-\frac{b}{2a},-\frac{D}{4a}\right)[/math][math]=\left(-\frac{b}{2a},-\frac{D}{4a}\right)[/math][br][b]4. Menentukan beberapa titik bantu jika diperlukan[br]5. Menghubungkan titik-titik yang diperoleh sehingga membentk kurva mulus[/b][br]

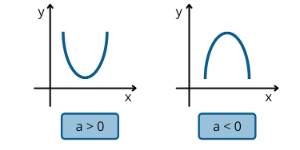
Berikut beberapa sifat-sifat grafik fungsi kuadrat berdasarkan bentuk umumnya. [br][b]1. Hubungan nilai [/b][math]a[/math][b] terhadap fungsi kuadrat[/b][br] Bentuk parabola fungsi kuadrat ditentukan nilai koefisien [math]a[/math] pada bentuk umum [math]f\left(x\right)=ax^2+bx+c[/math], yaitu:[br] [math]\bullet[/math] [math]a>0[/math] kurva parabola [b]membuka ke atas[/b] ([math]a[/math] positif)[br] [math]\bullet[/math] [math]a<0[/math] kurva parabola [b]membuka ke bawah[/b] ([math]a[/math] negatif)[br]

[b]2. Hubungan nilai [/b][math]b[/math][b] terhadap fungsi kuadrat [/b][br] Nilai [math]b[/math] merupakan koefisien [math]x[/math] yang menentukan posisi tiik puncak grafik fungsi kuadrat dalam koordinat kartesius. Posisi puncak ini disebut juga sebagai sumbu simetri karena membagi grafik menjadi dua bagian yang simetri.[br] Sifat grafik fungsi kuadrat [math]f\left(x\right)=ax^2+bx+c[/math] berdasarkan nilai [math]b[/math] yaitu[br] [math]\bullet[/math] Jika [math]b=0[/math], maka titik puncak [b]berada di sumbu y[/b] (sumbu simetrinya sama dengan sumbu y)[br] [math]\bullet[/math] Jika [math]a[/math] dan [math]b[/math] bertanda sama (positif dan positif / negatif dan negatif), maka titik puncak berada [b]di sebelah[br] kiri sumbu y[/b][br] [math]\bullet[/math] Jika [math]a[/math] dan [math]b[/math] bertanda beda (positif dan negatif), maka titik puncak berada [b]di sebelah kanan sumbu y[/b][br]

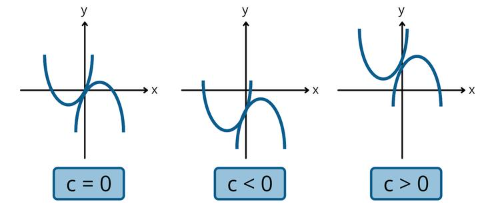
[b]3. Hubungan nilai [/b][math]c[/math][b] terhadap fungsi kuadrat[/b][br] Titik potong grafik fungsi kuadrat ditentukan oleh nilai konstanta [math]c[/math], pada bentuk umum fungsi kuadrat [math]f\left(x\right)=ax^2+bx+c[/math]. Nilai konstanta [math]c[/math] merupakan titik potong sumbu y dari kurva yang dibentuk fungsi kuadrat, yaitu titik [math]\left(0,c\right)[/math].[br] [math]\bullet[/math] [math]c>0[/math] kurva parabola memotong sumbu Y [b]positif[/b][br] [math]\bullet[/math] [math]c=0[/math] kurva parabola memotong sumbu Y [b]di titik pusat [/b][math]\left(0,0\right)[/math][br] [math]\bullet[/math] [math]c<0[/math] kurva parabola memotong sumbu Y [b]negatif[/b]

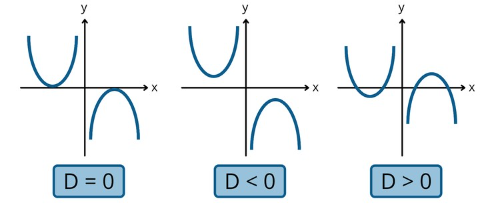
[b]4. Hubungan nilai [/b][math]D[/math][b] (Diskriminan) terhadap fungsi kuadrat[/b][br] Nilai diskriminan fungsi kuadrat [math]f(x)=ax^2+bx+c[/math] adalah [math]D=b^2-4ac[/math]. Nilai diskriminan suatu fungsi kuadrat dapat digunakan sebagai parameter karakteristik grafik berdasarkan titik potongnya di sumbu x. Karakteristik grafik fungsi kuadrat berdasarkan nilai diskriminannya [math](D)[/math] sebagai berikut.[br] [math]\bullet[/math] [math]D>0[/math], grafik fungsi kuadrat mempunyai [b]dua akar real berbeda[/b] [br] (grafik memotong sumbu X di [i][b]dua titik berbeda[/b][/i])[br] [math]\bullet[/math] [math]D=0[/math], grafik fungsi kuadrat mempunya [b]dua akar real kembar[br][/b] (grafik memotong sumbu X pada [i]satu titik [/i] dan merupakan sebuah titik puncak)[br] [math]\bullet[/math] [math]D<0[/math], grafik fungsi kuadrat mempunyai [b]akar imajiner[/b][br] (grafik [i]tidak memotong[/i] sumbu X). Terdapat 2 jenis karakteristik grafik kuadrat saat [math]D<0[/math][br] a. [b]Definit positif[br][/b] Saat [math]a>0[/math] dan [math]D<0[/math]. Grafik fungsi kuadrat berada di [i]atas sumbu X[/i][br] b. [b]Definit negatif[br][/b] Saat [math]a<0[/math] dan [math]D<0[/math]. Grafik fungsi kuadrat berada di [i]bawah sumbu X[/i]

[b]5. Titik Puncak Grafik Fungsi Kuadrat[/b][br] Titik puncak grafik parabola dari fungsi kuadrat dapat dihitung dari bentuk umumnya [math]f(x)=ax^2+bx+c[/math]. Titik puncak kurva parabola juga disebut titik ekstrim. Berikut rumus untuk mencari titik puncak grafik fungsi kuadrat, yaitu hitung titik ekstrim di sumbu C, lalu hitung nilai fungsinya untuk mendapat titik ekstrim sumbu Y. [br] [math]x_p=-\frac{b}{2a}[/math] dan [math]y_p=f\left(x_p\right)[/math][br] titik puncak = [math]\left(x_p,y_p\right)[/math]

Diketahui fungsi kuadrat [math]f\left(x\right)=x^2-2x-8[/math]. Tentukan: