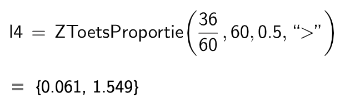
Testen omtrent een proportie
We maken gebruik van het commando [i]ZToetsProportie(steekproefverhouding, steekproefgrootte, hypothetische proportie, staart).[br][/i][br]De parameter [i]staart[/i] kan "<", ">" of "[math]\ne[/math]" zijn. Typ ook de aanhalingstekens! Dit duidt op de formulering van de alternatieve hypothese: linkszijdige test, rechtszijdige test of tweezijdige test.[br][br][b]Voorbeeld[/b][br]Er is bij 60 Vlaamse steden nagegaan of een bepaalde voorwaarde voldaan is. Bij 36 van hen was de voorwaarde in orde, bij de andere was dat niet zo. We willen nagaan of de werkelijke proportie van steden die aan die voorwaarde voldoen groter is dan 50% of niet. We nemen volgende hypothesen:[br][math]H_0:p\le0,5[/math][br][math]H_1:p>0,5[/math][br][br]We kunnen hier een test uitvoeren op basis van een normale verdeling aangezien [math]np_0=60\cdot0,5=30\ge5[/math] en [math]n\left(1-p_0\right)=60\cdot0,5=30\ge5[/math].
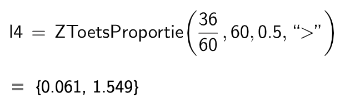
De testwaarde is hier 1,549. De kans dat je bij een standaardnormale verdeling een waarde groter dan 1,549 hebt, is 0,061. De P-waarde is dus 0,061. Als we als significantieniveau [math]\alpha=0,05[/math] kiezen, dan moeten we de nulhypothese aanvaarden die stelt dat de proportie 0,5 is want de P-waarde is groter dan [math]\alpha[/math].