1.Daire ve daire diliminin alanı M.7.3.3.3.
GİRİŞ
Bir noktaya bağlı kuzu otlamak istiyor.

Otlamak istediği alan nasıl bir şekil oluşturur?[br]Otlayabileceği alanı bulabilmek için hangi bilgilere ihtiyacımız var?
KEŞFETME // Aşağıdaki etkinlikle vakit geçirdikten sonra takip eden soruları cevaplayınız.
Bu uygulamada gördüğünüz (fark ettiğiniz) şey nedir?
Daire yeniden düzenlenip parça sayısı artırıldığında, yeniden düzenlenmiş parçaların oluşturduğu şekil neye benzemektedir?
Oluşan bu şeklin kenar uzunlukları neye eşittir?
Dikdörtgenin alan formülünü düşünün. Pek çok parçaya ayrılarak yeniden düzenlenmiş olan dairenin yeni şekli bir dikdörtgen gibi görünüyorsa, dairenin alanı ne olabilir?
dairenin alan formülünü oluşturalım
AÇIKLAMA
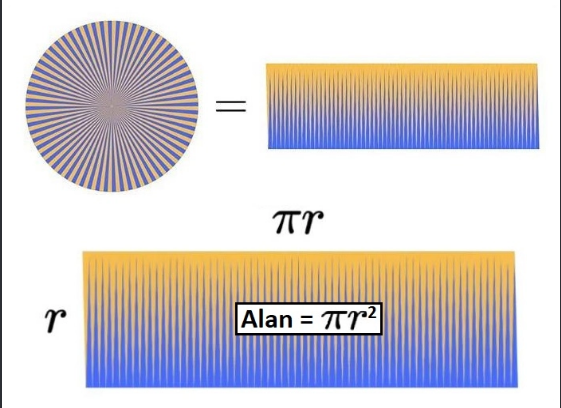
Dairenin alan formülü şeklinde ifade edilir.[br]A=πR2 [br]
DERİNLEŞTİRME // Kuzu otlamak istiyor :)

10 m[sup]2[/sup] 'lik alanda otlayarak doyan bir kuzu 2 metre uzunluğundaki iple ağaca bağlandığında bulunduğu yerde doyabilir mi?[br]([math]\prod[/math] =3 alınız)
2.Daire ve daire diliminin alanı M.7.3.3.3.
GİRİŞ

[b]Saat 03.00’ü göstermektedir. [/b]
Akrep ve yelkovan arasında kalan alan, saatin alanın ...........?
KEŞFETME
Açı sürgüsünü oynatınız.
Açı sürgüsünde açı büyüdükçe alan ......... ?
Açı sürgüsü hareket ettikçe yani daire diliminin açısı büyüdükçe [b]Daire Diliminin Alanı[/b] da büyümektedir. Yarıçap sürgüsü hareket ettikçe yani daire diliminin yarıçapı büyüdükçe [b]Daire Diliminin Alanı[/b] da büyümektedir
GeoGebra üzerinden Daire dilimi ve dairenin alanını yarıçapa bağlı olarak inceleyiniz.
Yarıçapı 2 ve açısı 180 derece olan daire diliminin alanını inceleyeniz. [br]GeoGebra gösterimi üzerinden inceleyip daire diliminin alanı dairenin alanının kaçta kaçıdır?
Yarıçapı 3 ve açısı 120 derece olan daire diliminin alanını inceleyiniz.[br]GeoGebra gösterimi üzerinden inceleyip dairenin alanı ve daire diliminin alanını söyleyiniz.[br]
Yarıçapı 3 ve açısı 90 derece olan daire diliminin alanını bulunuz.[br]GeoGebra gösterimi üzerinden inceleyip dairenin alanı ve daire diliminin alanını söyleyiniz.
AÇIKLAMA
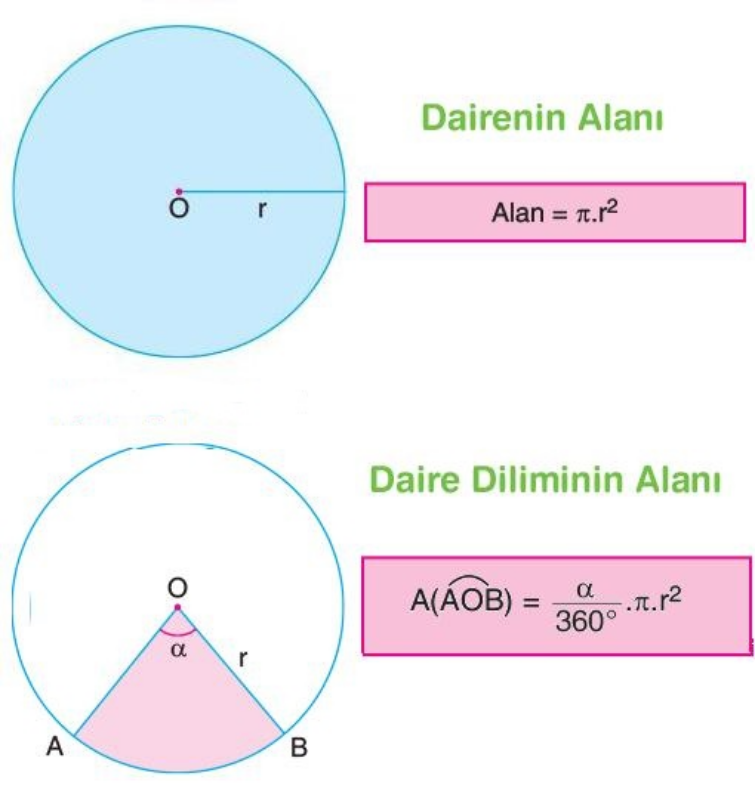
Daire; bir çember ile çemberin iç bölgesinin bileşiminden oluşan düzlem parçasıydı. İşte bu dairenin alanı da; yarıçap uzunluğunun (r) karesi ile π sayısının çarpımıdır. Yani O merkezli r yarıçaplı bir dairenin alanı;[br][b] A=π.r2[/b][br][s][/s]Daire diliminin yani dairenin içinden belirli bir parçasının alanı sorulurken eğer yarım veya çeyrek daire sorulursa formüle gerek kalmadan bütün dairenin alanını ikiye veya dörde bölerek yarım daireyi veya çeyrek daireyi bulabiliriz. Fakat belirli bir açıya sahip daire diliminin alanı sorulursa aşağıdaki formülü kullanmamız gerekir.[br]Bir merkez açıya karşılık gelen taralı kısmın alanı:[br][b] A=π.r2.α/360 [/b]formülüyle bulunur.[br] Bu formülde α yerine merkez açı ölçüsünü, r yerine yarıçap ölçüsünü, π yerine de π sayısını yazarız. Aslında daire diliminin alanı; dairenin alanının merkez açı kadarlık parçasını bulmaktır.[br]
DERİNLEŞTİRME
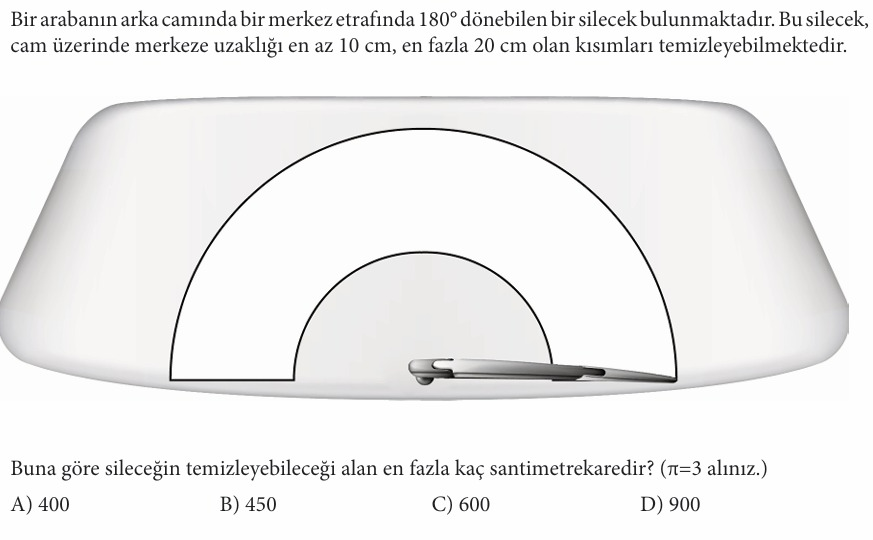
Yukarıdaki sorunun doğru cevabını işaretleyiniz.