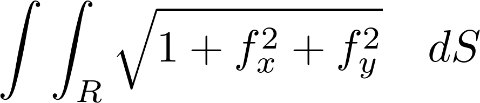
Área de una región de z=f(x,y)
Si f y sus primeras derivadas parciales f[sub]x[/sub] y f[sub]y[/sub] son continuas en la región cerrada U en el plano xy, entonces el área de la superficie S dada por z=f(x,y) sobre la región U viene dada por:[br][br][math]\int\int_R\sqrt{1+f_x^2+f_y^2}dS[/math][center][/center]
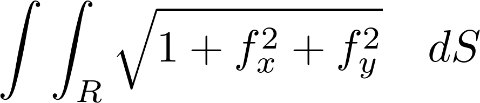
Para comprender la integral es útil recordar su semejanza con la longitud de arco:[br][br]Longitud de arco sobre el Eje x: [math]\int_a^bdx[/math][br][br]Longitud de arco en el plano xy: [math]\int_a^bds=\int_a^b\sqrt{1+f'\left(x\right)^2}dx[/math][br][br]Área en el plano xy: [math]\int\int_RdA[/math][br][br]Área de una superficie en el espacio: [math]\int\int_RdS=\int\int_R\sqrt{1+f_x^2+f_y^2}dA[/math]
Las integrales para calcular el área de una superficie son a menudo difíciles de calcular. En los ejemplos propuestos se pueden calcular fácilmente.