[br]Bei einer Gruppe aus [math]n[/math] Personen ([math]n\in\mathbb{N}[/math]) wird das Ereignis A: „Mindestens zwei Personen aus dieser Gruppe haben am gleichen Tag Geburtstag“ betrachtet. Das Geburtstagsparadoxon lässt sich durch eine Urne mit 365 Kugeln, die mit allen Tagen eines Jahres (ohne Schaltjahre) beschriftet sind, simulieren. Man zieht mit Zurücklegen und notiert sich jedes gezogene Datum.
Zeichne für den Fall [math]n=5[/math] ein vollständig beschriftetes Baumdiagramm und berechne [math]P(A)[/math].
[br][b]a) Berechne nun [/b][math]P(A)[/math][b] für [/b][math]n=10[/math][b]. [br][br]b) Gib einen Term an, der die Wahrscheinlichkeit für [/b][math]P(A)[/math][b] in Abhängigkeit von [/b][math]n[/math][b] angibt. [/b][br]
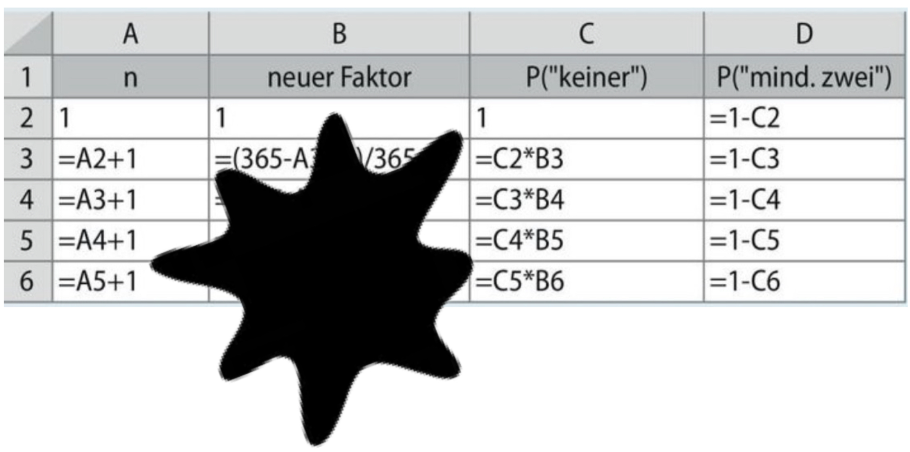
[b]Vervollständige die Tabelle auf deinem Arbeitsblatt.[/b]

[b]Löse das Ausgangsproblem aus dem Video mithilfe der Tabelle und bestimme die Anzahl der Personen, die man benötigt, damit die Wahrscheinlichkeit [/b][math]P(A)[/math][b] mehr als [/b][math]90\%[/math][b]beträgt. [/b]
[b]Ermittle mithilfe des Applets, ab welcher Personenzahl n die Wahrscheinlichkeit [/b][math]P(A)>99\%[/math][b] ist. [/b][br][br]Erklärung zum Applet:[br]Verändere den horizonatlen Schieberegler um die Anzahl der untersuchten Personen zu verändern.[br][br]Verändere den vertikalen Schieberegler um ein Sicherheitsintervall zu erstellen.[br][br]Mit dem Button "Spu löschen" bringst du das Arbeitsbaltt wieder in den Ausgangszustand.


