Parametrisierung
Kernpunkte
- [b]Parametrisierung einer Kurve:[br][/b]Weg, dessen Graph genau die Kurve ist.[br]Es gibt mehrere Parametrisierungen zu derselben Kurve
Arbeitsaufträge
[b]Aufgabe 1:[/b][br]Sei [math]f:\left[0,5\right]\rightarrow\mathbb{R},f\left(x\right)=2x^3-x^2+3[/math]. Der Graph dieser eindimensionalen Funktion beschreibt eine Kurve im [math]\mathbb{R}^2[/math]. Gib eine Parametrisierung für diese Kurve an.[br]Wie bist du dabei vorgegangen?
[b]Aufgabe 2:[/b][br]Wie viele Parametrisierungen für eine gegebene Kurve gibts es?
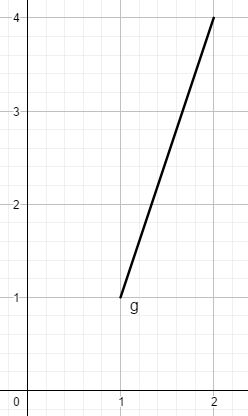
[b]Aufgabe 3:[/b][br]Gib mindestens 3 unterschiedliche Parametrisierungen für die folgende Kurve an.

Hilfestellung
Bonusaufgaben
[b]Bonusaufgabe 1:[/b][br]Wie kann man aus einer gegebenen Parametrisierung [math]f:\left[a,b\right]\rightarrow\mathbb{R}^3,f\left(t\right)=\left(\begin{matrix}x\left(t\right)\\y\left(t\right)\\z\left(t\right)\end{matrix}\right)[/math] weitere Parametrisierungen herleiten?[br][size=85][b]Tipp:[/b] Die Wege [math]f:\left[0,1\right]\rightarrow\mathbb{R}^3,f\left(t\right)=\left(\begin{matrix}t\\2t\\t^2\end{matrix}\right)[/math] und [math]g:\left[1,2\right]\rightarrow\mathbb{R}^3,g\left(t\right)=\left(\begin{matrix}t-1\\2\cdot\left(t-1\right)\\\left(t-1\right)^2\end{matrix}\right)[/math] parametrisieren dieselbe Kurve.[/size]
[b]Bonusaufgabe 2:[br][/b]Begründe die Anzahl der Parametrisierungen für eine gegebene Kurve.