Funzioni inverse e loro derivate
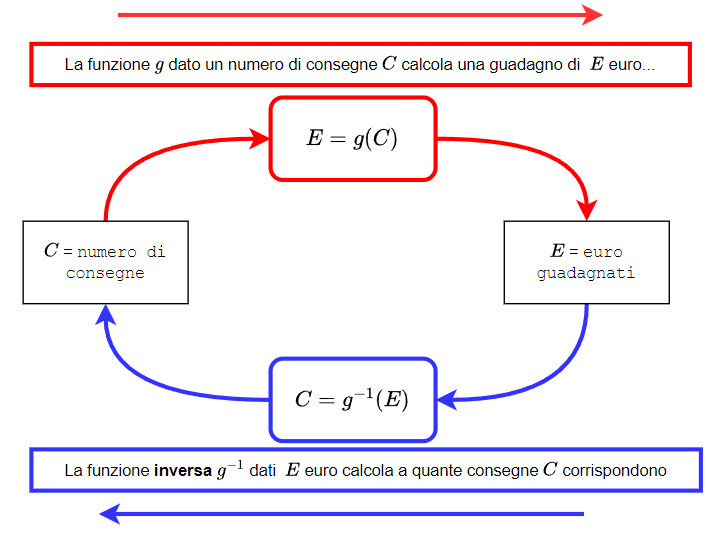
[size=150][color=#ff0000]INTRODUZIONE[/color][/size][br]Una funzione è una relazione che dato un valore di input permette di calcolare un corrispondente valore di output come risultato. [b]La funzione inversa[/b], [u]quando[/u] può essere definita (cioè quando la funzione è [b]invertibile[/b]), è la relazione che dato un particolare valore di output permette di ricavare il valore di input che l'ha generato.[br][br]Puoi rivedere questi argomenti qui:[br][b]funzione inversa[/b]: [url=https://www.geogebra.org/m/ahCuGvXP#material/ujautySS]https://www.geogebra.org/m/ahCuGvXP#material/ujautySS[/url][br][b]invertibilità delle funzioni[/b]: [url=https://www.geogebra.org/m/ahCuGvXP#material/yxajpkkp]https://www.geogebra.org/m/ahCuGvXP#material/yxajpkkp[br][br][/url][b][color=#ff0000]Lo scopo che ci proponiamo ora è calcolare la derivata della funzione inversa utilizzando la derivata della funzione di partenza, che supponiamo di saper calcolare[/color][/b]. [br]La regola che troveremo infatti varrà sempre, anche nel caso in cui sappiamo derivare la funzione inversa (sarà così nel primo esempio, scelto appositamente per permetterci di verificare che la nuova regola funziona), ma sarà particolarmente comoda quando conosciamo la derivata di una funzione ma non quella della sua inversa. [br][br][size=150][color=#ff0000]UN PRIMO ESEMPIO[/color][/size][br]Riprendiamo l'esempio proposto nella pagina linkata sopra, dove abbiamo immaginato una funzione [math]\large{E=g(C)}[/math] che esprima come calcolare gli euro guadagnati [math]\large{E}[/math] in base al numero delle consegne effettuate [math]\large{C}[/math], e la corrispondente funzione inversa [math]\large{C=g^{-1}(E)}[/math] che partendo dal guadagno ottenuto permette di risalire alle consegne svolte.

Poiché la funzione inversa scambia input e risultato, i punti che costituiscono il suo grafico hanno ascisse ed ordinate scambiate tra loro rispetto a quelli della funzione diretta. Questo è molto utile per [b]capire come possiamo ottenere la derivata della funzione inversa partendo da quella della funzione di riferimento[/b].[br][br]Vediamo un esempio nel grafico sotto; come [b]esempio[/b] abbiamo ipotizzato che la funzione diretta che fornisce il guadagno partendo dal numero di consegne sia un [b]logaritmo naturale[/b], di conseguenza la funzione[b] inversa[/b] che permette di calcolare il numero di consegne partendo dal guadagno desiderato sarà l'inversa del logaritmo, cioè l'[b]esponenziale[/b]. Per il momento questo ci interessa relativamente e ci basta osservare com'è il grafico della inversa rispetto alla funzione di partenza.[br][br][size=85]NOTA: la scrittura [math]E=E(C)[/math] indica in modo esplicito che gli euro guadagnati [math]E[/math] dipendono dal numero di consegne [math]C[/math]; allo stesso modo [math]C=C(E)[/math] indica che le consegne da fare [math]C[/math] dipendono dagli euro [math]E[/math] che desideriamo ottenere; usiamo poi un terzo nome [math]g[/math] per la funzione per esprimere in modo più chiaro la funzione e la sua inversa.[br][/size][br]
[size=85]Nel grafico vediamo la funzione originale [math]\large{\textcolor{red}{E=g(C)}}[/math] che esprime gli Euro in funzione delle Consegne effettuate e la sua inversa [math]\large{\textcolor{#007700}{C=g^{-1}(E)}}[/math]. La prima ha [math]\large{C}[/math] sulle [math]\large{x}[/math] e [math]\large{E}[/math] sulle [math]\large{y}[/math], mentre la sua inversa ha le variabili collocate sugli assi scambiati, ma le si riporta sullo stesso piano per mettere in evidenza che i loro punti hanno le coordinate scambiate tra loro; [b]questo ci permette di capire che anche le variazioni che compaiono nel rapporto incrementale e nella derivata di scambiano di posizione, generando così per la funzione inversa la frazione reciproca[/b]. [/size][br][br]La derivata indica la velocità con cui cambia il risultato (output) rispetto alla variazione dell'input, nell'esempio la velocità con cui il guadagno cambia al variare del numero di consegne, ed è associata al rapporto tra le variazioni di queste due quantità. [br][br][math]\Large{y=f(x) \qquad \rightarrow \qquad y'=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \frac{dy}{dx} = \frac{d\mbox{ output}}{d\mbox{ input}}}[/math][br][br][b]Poiché nella funzione inversa il ruolo delle due variabili è scambiato, il rapporto risulta invertito e quindi [color=#ff0000]la derivata della funzione inversa è il reciproco della derivata della funzione di partenza; questo ci permette di calcolare la derivata di una funzione che non conosciamo, se essa è l'inversa di una funzione di cui sappiamo la derivata[/color][/b]. [br][br]Per chiarire cosa significa questo dal punto di vista del calcolo facciamo un esempio concreto di cui sappiamo già il risultato, così possiamo capire e verificare come funziona il metodo. Supponiamo che la funzione di partenza sia una logaritmica ([color=red][b]il grafico rosso[/b][/color] nell'esempio sopra).[br][br][math]\Large{\textcolor{red}{E=g(C)= \ln C} \qquad \qquad \qquad \qquad (1)}[/math][br][br]Di conseguenza la funzione inversa è l'esponenziale [br][br][math]\Large{\textcolor{#007700}{C=C(E)=g^{-1}(E)= e^E} \qquad \qquad \qquad \qquad (2)}[/math][br][br]Noi ovviamente sappiamo che la derivata dell'esponenziale è [math]\large{C'(E)=\frac{d e^E}{dE}= e^E }[/math], ma [b][color=#ff0000]facciamo finta di non saperlo e di conoscere solo la derivata del logaritmo; riusciamo a calcolare la derivata di [math]\Large{C}[/math] sfruttando il fatto che è l'inversa di una funzione che sappiamo derivare?[br][/color][/b] [br][br]Per quanto abbiamo visto la derivata è il reciproco della derivata della funzione di partenza[br][br][math]\Large{C'(E)=\frac{dC}{dE} = \frac{1}{\frac{dE}{dC}}=\frac{1}{\frac{d \ln C}{dC}} \qquad \qquad \qquad (3)}[/math][br][br]Abbiamo ipotizzato di conoscere la derivata del logaritmo [br][math]\Large{\textcolor{red}{E'=g'(C)= \frac{d \ln C}{dC}=\frac{1}{C}} \qquad \qquad \qquad \qquad (4)}[/math][br][br]sostituendola nella [math]\Large{(3)}[/math] otteniamo[br][br][math]\Large{C'(E)=\frac{dC}{dE} = \frac{1}{\frac{dE}{dC}}=\frac{1}{\frac{d \ln C}{dC}}= \frac{1}{\frac{1}{C}}=\textcolor{#007700}{C = e^E} \qquad \qquad \qquad (5)}[/math][br][br]Nell'ultimo passaggio evidenziato in verde abbiamo sostituito al posto di [math]\large{C}[/math] la sua espressione, data dalla [math]\large{(2)}[/math] per esprimere in modo esplicito la dipendenza di [math]\large{C'(E)}[/math] da [math]\large{E}[/math]. [br][br]Come previsto abbiamo trovato che la derivata di [math]\large{C(E)}[/math] coincide con l'esponenziale stesso, ma abbiamo ottenuto questo risultato attraverso il ragionamento logico basato sul concetto di funzione inversa.
ORA PROVA TU
Prova ad applicare la regola della derivazione inversa per calcolare la derivata di [math]\large{y=\sqrt{x}}[/math], considerandola come inversa di [math]\large{y=x^2}[/math]. [b]Per non confonderti puoi usare lettere alternative:[/b] [b][color=#ff0000]calcola la derivata di [math]\large{C=C(E)=\sqrt{E}}[/math] considerandola l'inversa di[/color][/b] [math]\large{E=E(C)=C^2}[/math][br][br][color=#0000ff]Non guardare subito [tutta] la soluzione! Provaci, prima![/color][br][br][b][color=#0000ff]SOLUZIONE[br][/color][/b]La regola della derivata dell'inversa ci dice che[br][math]\large{C'(E)=\frac{1}{E'(C)}}[/math][br][br]Sappiamo che la derivata di [math]\large{E(C)=C^2}[/math] vale [math]\large{E'(C)=2C}[/math], quindi abbiamo[br][br][math]\large{C'(E)=\frac{1}{\textcolor{red}{E'(C)}}=\frac{1}{\textcolor{red}{2C}}}[/math][br][br]La derivata [math]\large{C'(E)}[/math] deve essere un'espressione che contiene [math]\large{E}[/math], non [math]\large{C}[/math], quindi al posto di [math]\large{C}[/math] sostituiamo la sua espressione [math]\large{\textcolor{blue}{C=C(E)=\sqrt{E}}}[/math] ed otteniamo il risultato finale[br][br][math]\large{C'(E)=\frac{1}{\textcolor{red}{E'(C)}}=\frac{1}{\textcolor{red}{2\textcolor{blue}{C}}}=\frac{1}{\textcolor{red}{2\textcolor{blue}{\sqrt{E}}}}}[/math][br][br]La derivata di [math]\large{\sqrt{E} = E^\frac{1}{2}}[/math] vale proprio [math]\large{\frac{1}{2}E^{-\frac{1}{2}}}[/math], quindi abbiamo applicato correttamente il metodo.
[size=150][color=#ff0000]UN ESEMPIO PIÙ COMPLESSO: DERIVATA DELL'ARCOSENO[/color][/size][br][br]Finora abbiamo applicato il metodo a funzioni che conoscevamo già, non ci ha dato niente di nuovo ma serviva per allenarci. Ora vediamo un caso in cui il metodo ci permette di ottenere una derivata che non conosciamo. Supponiamo ora che la funzione del guadagno sia data da [br][br][math]\Large{\textcolor{red}{E(C)=\sin C}\qquad \qquad \qquad \qquad (5)}[/math][br][br][size=85]NOTA: facciamo riferimento a questo esempio concreto per non dover utilizzare le lettere [math]\large{x}[/math] ed [math]\large{y}[/math]: esse sono strettamente associate al concetto rispettivamente di input ed output, e poiché considerare la funzione inversa implica scambiare questi ruoli utilizzare tali lettere potrebbero generare confusione. [/size][br][br]La funzione inversa è [math]\large{\textcolor{#009900}{C(E)=\arcsin C}}[/math]; [b]al contrario di quanto accadeva nel primo esempio, non conosciamo la derivata di questa funzione: per ottenerla siamo quindi costretti ad utilizzare la procedura legata al concetto di funzione inversa[/b].[br][br]Esprimiamo quindi la derivata di [math]\large{C(E)}[/math] mettendo in evidenza il fatto che è la funzione inversa di [math]\large{E(C)=\sin C}[/math], similmente a quanto abbiamo fatto nell'esempio precedente.[br][br][math]\Large{C'(E)=\frac{dC}{dE} = \frac{1}{\frac{dE}{dC}}=\frac{1}{\frac{d \sin C}{dC}}= \frac{1}{\cos C}}\qquad \qquad \qquad \qquad (6)[/math][br][br][b]Il prossimo passo, [color=#ff0000]che in questo caso non è semplice[/color], è esprimere la derivata che abbiamo ottenuto con un'espressione che dipende da [/b][math]\large{E}[/math][b], l'input della funzione inversa[/b]. Per fare questo dobbiamo riscrivere [math]\large{\frac{1}{\cos C}}[/math] facendo comparire [math]\large{E}[/math], cioè [math]\large{E(C)=\sin C}[/math] come abbiamo fatto negli altri esempi. Ci appoggiamo alla prima legge fondamentale della goniometria:[br][br][math]\large{\textcolor{blue}{\sin ^2 C + \cos ^2 C = 1 \quad \rightarrow \quad \cos^2 C = 1-\sin ^2 C \quad \rightarrow \quad \cos C = \pm \sqrt{1-\sin ^2 C}}\qquad \qquad \qquad \qquad (7)}[/math][br][br]Abbiamo la possibilità di sostituire al posto di [math]\large{\cos C}[/math] un'espressione che contiene [math]\large{\sin C}[/math], [b]ma in tale espressione vi è un doppio segno che complicherebbe molto le cose[/b]. Fortunatamente non dovremo gestirlo, ed in questo ci aiuta il fatto che [b]è possibile invertire una funzione (cioè esiste la sua inversa) [color=#ff0000]solo se anche la relazione inversa è una funzione, cioè genera un solo risultato per ogni input scelto[/color][/b]. [br][br]Per quanto riguarda il nostro esempio abbiamo visto (in [b]questa [/b]pagina https://www.geogebra.org/m/ahCuGvXP#material/yxajpkkp) che il seno non è invertibile in tutto il suo dominio, perchè dato un valore del seno vi sono infiniti angoli che hanno come seno quel valore: [b]il seno è invertibile in un intervallo ristretto in cui la funzione è biunivoca[/b].
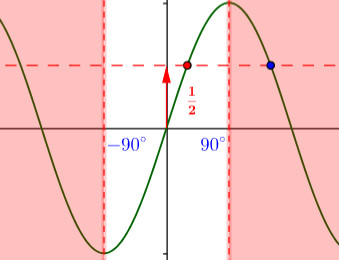
Il seno non è una funzione biunivoca: se ad un angolo corrisponde un solo seno [math]\left ( \textcolor{red}{\mbox{ad esempio }\sin(30°)=\frac{1}{2}}\right )[/math], a quel valore del seno corrispondono infiniti angoli [math]\left ( \mbox{\textcolor{blue}\mbox{ad esempio anche 120° ha seno pari a }\frac{1}{2}}\right )[/math]. Quindi in generale la funzione seno non è invertibile, perchè la relazione inversa genera infiniti output per ogni input (per ogni valore del seno vi sono infiniti angoli con quel seno). [br][br]Se consideriamo la funzione seno nell'intervallo tra -90° e +90°, però eliminiamo questo problema: in quell'intervallo per ogni valore del seno vi è un solo angolo che ha quel seno e quindi anche la relazione inversa un risultato univoco ed è una funzione.
[b]Nell'intervallo di invertibilità del seno, cioè tra -90° e +90°, il coseno è sempre positivo, quindi possiamo invertire la prima legge fondamentale potendo scegliere il segno + ed eliminando l'ambiguità[/b]. Riprendiamo quindi il calcolo [math]\large{(6)}[/math] sostituendo nell'ultimo passaggio la scrittura [math]\large{\textcolor{blue}{(7)}}[/math], con il solo segno + per quanto appena detto.[br][br][math]\Large{C'(E)=\frac{dC}{dE} = \frac{1}{\frac{dE}{dC}}=\frac{1}{\frac{d \sin C}{dC}}= \frac{1}{\textcolor{blue}{\cos C}}=\frac{1}{\textcolor{blue}{+\sqrt{1-\sin ^2 C}}} }[/math][br][br]A questo punto possiamo utilizzare la definizione [math]\large{\textcolor{red}{(5)}}[/math] della funzione di partenza per riscrivere la derivata dell'arcoseno:[br][br][math]\Large{C'(E)=\frac{d \arcsin C}{dE} = \frac{1}{\frac{dE}{dC}}=\frac{1}{\frac{d \sin C}{dC}}= \frac{1}{\textcolor{blue}{\cos C}}=\frac{1}{\textcolor{blue}{+\sqrt{1-\textcolor{red}{\sin ^2 C}}}}=\frac{1}{\sqrt{1-\textcolor{red}{E}^2}} }[/math][br][br]Esprimendo il risultato con le variabili abituali [math]\large{x\mbox{ e } y}[/math], ricordando che per la nostra funzione inversa l'input [math]\large{x}[/math] coincide con [math]\large{E}[/math] e l'output [math]\large{y}[/math] è rappresentato da [math]\large{C}[/math], abbiamo che[br][br][math]\Large{y'=D[\arcsin(x)]=\frac{d \arcsin x}{dx} = \frac{1}{\sqrt{1-x^2}}\qquad \qquad \qquad \qquad (8) }[/math][br][br]
[color=#ff0000][size=150]LE DERIVATE DELLE ALTRE INVERSE GONIOMETRICHE[/size][/color][br]In modo del tutto analogo se consideriamo [br][br][math]\Large{\textcolor{red}{E(C)=\cos C}\qquad \qquad \qquad \qquad (9)}[/math][br][br]abbiamo[br][br][math]\Large{C'(E)=\frac{dC}{dE} = \frac{1}{\frac{dE}{dC}}=\frac{1}{\frac{d \cos C}{dC}} = \frac{1}{- \sin C}}\qquad \qquad \qquad \qquad (10)[/math][br][br]La prima legge fondamentale si inverte in modo identico e ci dà[br][br][math]\large{\textcolor{blue}{\sin ^2 C + \cos ^2 C = 1 \quad \rightarrow \quad \sin^2 C = 1-\cos ^2 C \quad \rightarrow \quad \sin C = \pm \sqrt{1-\cos ^2 C}}\qquad \qquad \qquad \qquad (7a)}[/math][br][br]Anche il coseno ha un problema di invertibilità analogo a quello del seno, risolvendo il quale possiamo disambiguare il doppio segno che abbiamo ottenuto.
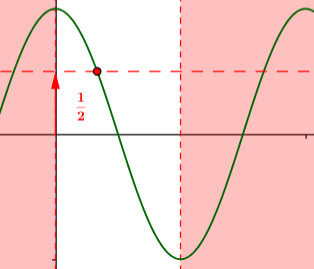
L'intervallo di invertibilità scelto convenzionalmente per per il coseno è tra 0° e 180°, perchè in esso ciascun possibile valore del coseno è ottenuto da un solo angolo (l'intervallo del seno, tra -90° e +90° non funziona perchè due angoli opposti hanno lo stesso coseno). [br][br][b]In questo intervallo il seno è sempre positivo, e questo ci permette di eliminare il doppio segno ottenuto invertendo la prima legge fondamentale della goniometria.[/b]
Sostituendo l'espressione [math]\large{\textcolor{blue}{(7a)}}[/math] (con il solo segno +, [b]attenzione al segno - che precede il seno dovuto alla derivata del coseno[/b]) nella [math]\large{(10)}[/math], e sostituendovi poi la [math]\large{\textcolor{red}{(9)}}[/math] otteniamo quindi:[br][br][math]\Large{C'(E)=\frac{d \arccos E}{dE} = \frac{1}{\frac{dE}{dC}}=\frac{1}{\frac{d \cos C}{dC}} = \frac{1}{- \textcolor{blue}{\sin C}} = \frac{1}{- \textcolor{blue}{ \sqrt{1-\textcolor{red}{\cos} ^2 \textcolor{red}{C}}}}=\frac{1}{- \sqrt{1-\textcolor{red}{E}^2}}}[/math][br][br]cioè, in termini delle usuali variabili [math]\large{x\mbox{ e } y}[/math]:[br][br][math]\Large{y'=D[\arccos(x)]=\frac{d \arccos x}{dx} = \frac{1}{-\sqrt{1-x^2}} }\qquad \qquad \qquad \qquad (11)[/math].[br][br]Per quanto riguarda infine la tangente abbiamo[br][br][math]\Large{\textcolor{red}{E(C)=\tan C}\qquad \qquad \qquad \qquad (12)}[/math][br][br]il calcolo della derivata inversa ci dà[br][br][math]\Large{C'(E)=\frac{dC}{dE} = \frac{1}{\frac{dE}{dC}}=\frac{1}{\frac{d \tan C}{dC}} = \frac{1}{1+ \textcolor{red}{\tan^2 C}} = \frac{1}{1+ \textcolor{red}{E}^2}}[/math][br][br]Risulta abbastanza immediato perchè abbiamo scelto la forma [math]\large{1+ \tan^2 C}[/math] per la derivata della tangente, dato in essa abbiamo potuto sostituire direttamente l'espressione [math]\large{\textcolor{red}{(12)}}[/math] ottenedo il risultato finale, che espresso nella variabili [math]\large{x\mbox{ e } y}[/math] è quindi[br][br][math]\Large{y'=D[\arctan(x)]=\frac{d \arctan x}{dx} = \frac{1}{1+x^2} }\qquad \qquad \qquad \qquad (12)[/math][br][br][br]