Triangle Congruence Investigation

Caroline Psutka, Cheryl Lee, Jul 21, 2022

What consecutive triangle parts need to be congruent in order to show that two triangles are congruent? These applets allow students to explore whether triangle relationships (SSS, AAA, SAS, RHS, SSA, ASA, AAS) force triangles to be congruent or not. Are you able to create a non-congruent pair of triangles?

Table of Contents

  1. Introduction
    1. Congruent Figures (Recap)
    2. Is there a shorter way?
  2. SSS
    1. SSS - 3 pairs of congruent sides
    2. SSS Reflections
  3. AAA
    1. AAA- 3 pairs of congruent angles
    2. AAA Reflections
  4. SAS
    1. SAS- 2 Congruent Sides with Congruent Angle in Between
    2. SAS Reflections
  5. RHS
    1. RHS- Right-angled Triangles only, 1 pair of congruent hypotenuse and 1 pair of congruent sides
    2. RHS Reflections
  6. SSA
    1. SSA- 2 Congruent Sides with a Congruent Angle NOT in between
    2. SSA Reflections
  7. ASA and AAS
    1. ASA- 2 Pairs of Congruent Angles with a Congruent Side in between
    2. AAS- 2 Pairs of Congruent Angles with a Congruent Side NOT inbetween
    3. ASA and AAS Reflections
  8. Check for Understanding
    1. Check for understanding

1.

Introduction

  • 1. Congruent Figures (Recap)
  • 2. Is there a shorter way?

1.1.

Congruent Figures (Recap)

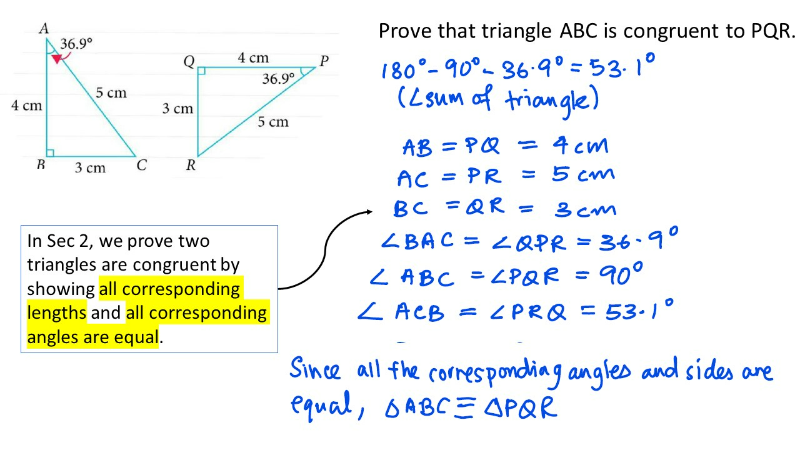
In Secondary 2, we have learned that congruent figures have exactly the same shape and size.[br][br]This means that all the corresponding lengths, as well as the corresponding angles of congruent triangles, are equal.[br][br]Below is an example of how we prove two triangles are congruent in Sec 2.
– Cheryl Lee

1.2.

–

2.

SSS

  • 1. SSS - 3 pairs of congruent sides
  • 2. SSS Reflections

2.1.

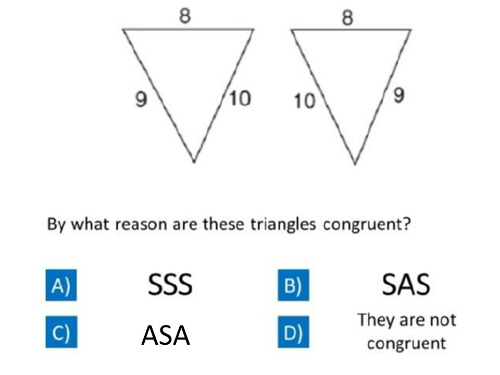
SSS - 3 pairs of congruent sides

Move the vertex, are you able to form different triangles?[br]
– Cheryl Lee, Caroline Psutka

2.2.

–

3.

AAA

  • 1. AAA- 3 pairs of congruent angles
  • 2. AAA Reflections

3.1.

AAA- 3 pairs of congruent angles

Move the vertex, are we able to form triangles with equal corresponding angles but are not congruent?
– Cheryl Lee, Caroline Psutka

3.2.

–

4.

SAS

  • 1. SAS- 2 Congruent Sides with Congruent Angle in Between
  • 2. SAS Reflections

4.1.

SAS- 2 Congruent Sides with Congruent Angle in Between

Move the point and extend the line.[br]If we fixed 2 lengths and an included angle, are we able to form different triangles?
– Cheryl Lee, Caroline Psutka

4.2.

–

5.

RHS

  • 1. RHS- Right-angled Triangles only, 1 pair of congruent hypotenuse and 1 pair of congruent sides
  • 2. RHS Reflections

5.1.

RHS- Right-angled Triangles only, 1 pair of congruent hypotenuse and 1 pair of congruent sides

Can different triangles be formed if the 90-degree, length of one side, and length of the hypotenuse are fixed?
– Cheryl Lee, Caroline Psutka

5.2.

–

6.

SSA

  • 1. SSA- 2 Congruent Sides with a Congruent Angle NOT in between
  • 2. SSA Reflections

6.1.

SSA- 2 Congruent Sides with a Congruent Angle NOT in between

Move the vertex, can different triangles be formed if we fixed the length of two sides and one angle?
– Cheryl Lee, Caroline Psutka

6.2.

–

7.

ASA and AAS

  • 1. ASA- 2 Pairs of Congruent Angles with a Congruent Side in between
  • 2. AAS- 2 Pairs of Congruent Angles with a Congruent Side NOT inbetween
  • 3. ASA and AAS Reflections

7.1.

ASA- 2 Pairs of Congruent Angles with a Congruent Side in between

Can different triangles be formed if we fixed two angles and a side that is between the two angles?
– Cheryl Lee, Caroline Psutka

7.2.

–

7.3.

–

8.

Check for Understanding

  • 1. Check for understanding

8.1.

Check for understanding

Question 1
Which of the following are tests of congruency?
Question 2
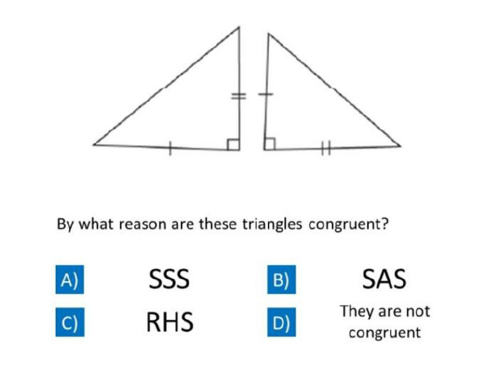
Question 3
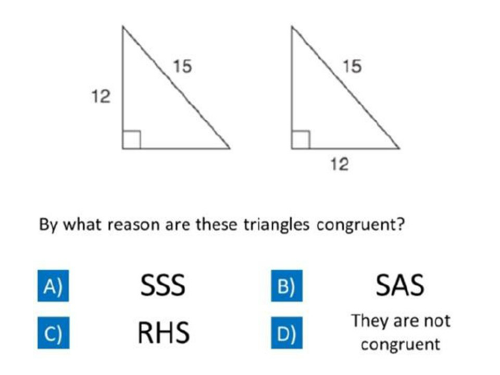
Question 4
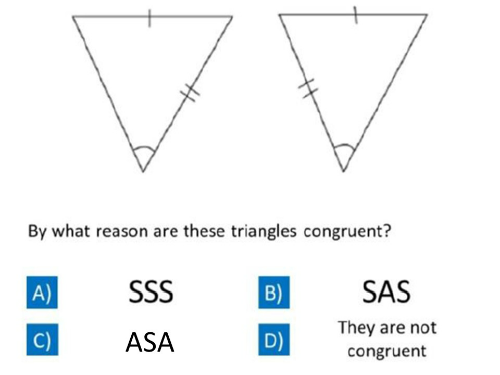
Question 5
– Cheryl Lee

Information