ภาคตัดกรวย
ชุดกิจกรรมการเรียนรู้ด้วยโปรแกรม Geogebra เรื่องภาคตัดกรวย ชั้นมัธยมศึกษาปีที่ 4 ประกอบด้วย - ชุดกิจกรรมที่ 1 เรื่องสนุกกับการเลื่อนแกนทางขนาน - ชุดกิจกรรมที่ 2 เรื่องแม่นสมการวงกลม - ชุดกิจกรรมที่ 3 เรื่องนำทางพาราโบลา - ชุดกิจกรรมที่ 4 เรื่องเปิดมุมมองวงรี - ชุดกิจกรรมที่ 5 เรื่องไขรหัสไฮเพอร์โบลา
Table of Contents
- แบบทดสอบก่อนเรียน
- แบบทดสอบก่อนเรียน
- ชุดกิจกรรมที่ 1 เรื่องสนุกกับการเลื่อนแกนทางขนาน
- การเลื่อนแกนทางขนาน
- การเลื่อนแกนทางขนาน กราฟพาราโบลา
- การเลื่อนแกนทางขนาน กราฟของสมการค่าสัมบูรณ์
- ชุดกิจกรรมที่ 2 เรื่องแม่นสมการวงกลม
- กำเนิดภาคตัดกรวย
- สำเนาของ สมการวงกลม C(0,0)
- สมการวงกลม C(h,k)
- รูปแบบทั่วไปของสมการวงกลม
- กิจกรรม "วัดขนาดล้อด้วยสมการวงกลม"
- ชุดกิจกรรมที่ 3 เรื่องนำทางพาราโบลา
- กำเนิดพาราโบลา
- พาราโบลา จุดยอด V(0,0)
- พาราโบลา จุดยอด V(h,k)
- รูปแบบทั่วไปของสมการพาราโบลา
- กิจกรรม "ลูกจะเข้าห่วงไหม"
- ชุดกิจกรรมที่ 4 เรื่องเปิดมุมมองวงรี
- กำเนิดวงรี
- สมการวงรี C(0,0)
- สมการวงรี C(h,k)
- รูปแบบทั่วไปของวงรี
- กิจกรรม “เส้นทางดวงดาว”
- ชุดกิจกรรมที่ 5 เรื่องไขรหัสไฮเพอร์โบลา
- กำเนิดไฮเพอร์โบลา
- ไฮเพอร์โบลา C(0,0)
- ไฮเพอร์โบลา C(h,k)
- รูปแบบทั่วไปของไฮเพอร์โบลา
- กิจกรรม “ไฮเพอร์โบลากับโรงไฟฟ้านิวเคลียร์”
- แบบทดสอบหลังเรียน
- ตอนที่ 1 แบบทดสอบแบบปรนัย
- ตอนที่ 2 แบบทดสอบอัตนัย
- ตอนที่ 3 แสดงวิธีทำ
แบบทดสอบก่อนเรียน
[b]แบบทดสอบวัดผลสัมฤทธิ์ทางการเรียน (ก่อนเรียน)[br]คำชี้แจง ให้นักเรียนเลือกคำตอบที่ถูกต้องที่สุด [/b]
1. ให้ [math]x^2+y^2-16x-16y+64=0[/math] จัดรูปเป็นสมการวงกลมมาตรฐานตามข้อใด
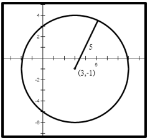
2.จากรูปด้านบน วงกลมต่อไปนี้ตรงกับสมการใด
3.สมการของวงกลมที่มีจุดศูนย์กลางอยู่ที่จุด [math]\left(-4,2\right)[/math] และสัมผัสกับเส้นตรง [math]3x-4y+40=0[/math] คือสมการในข้อใ
4.กราฟของสมการ [math]x^2+y^2-6x+2y-15=0[/math] เป็นวงกลมหรือไม่ ถ้าเป็นจุดศูนย์กลางและรัศมีมีค่าเท่าใด
5.จงหาจุดศูนย์กลางและรัศมีของ [math]2x^2+2y^2-3x+4y+3=0[/math]
6.ข้อใดคือสมการของพาราโบลาที่มีไดเรกตริกซ์คือเส้นตรง [math]x=12[/math] และโฟกัสที่จุด (2,0)
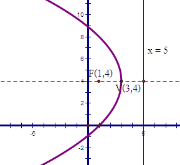
7.จากรูป กราฟพาราโบลาต่อไปนี้ตรงกับสมการใด
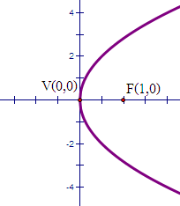
8.จากรูป กราฟพาราโบลาต่อไปนี้ตรงกับสมการใด
9.จากสมการ [math]y^2-12x=0[/math] จุดยอด และจุดโฟกัส ของพาราโบลาตรงกับข้อใด
10. พาราโบลามีจุดยอดอยู่ที่จุด (-2,-6) และโฟกัสอยู่ที่จุด (-2,-2) สมการไดเรกตริกซ์ตรงกับข้อใด
การเลื่อนแกนทางขนาน
การสำรวจการเลื่อนแกนทางขนานด้วยโปรแกรม Geogebra
[b]คำชี้แจง[/b] ให้นักเรียน[br]1. ปรับแถบเลื่อน O'(h,k) เป็นจุดกำเนิดใหม่ของระบบพิกัด[br]2. เลื่อนจุด P(x,y) ตามโจทย์[br]3. คำนวณหาพิกัดของจุดใหม่ (x',y') เมื่อเทียบกับแกนพิกัดใหม่ และตอบคำถาม
สำรวจการเลื่อนแกนทางขนานด้วยโปรแกรม Geogebra
1.ถ้าเลื่อนจุดกำเนิดไปที่ O'(2,0) จงหาพิกัดใหม่ของจุด P(5,3)
2.ถ้าเลื่อนจุดกำเนิดไปที่ O'(-1,2) จงหาพิกัดใหม่ของจุด P(-3,3)
3.ถ้าเลื่อนจุดกำเนิดไปที่ O'(4,3) และ (5,-1) เป็นจุดพิกัดของจุดเมื่อเทียบกับแกนพิกัดใหม่ จงหาพิกัด P ของจุดเมื่อเทียบกับแกนเดิม
4.จากการสังเกต พิกัด x ของจุดในระบบใหม่ (x') สัมพันธ์กับพิกัด x เดิมและค่า h อย่างไร
5.จากการสังเกต พิกัด y ของจุดในระบบใหม่ (y') สัมพันธ์กับพิกัด y เดิมและค่า k อย่างไร[br][br][br]
กำเนิดภาคตัดกรวย
กำเนิดภาคตัดกรวย ด้วยโปรแกรม Geogebra
[u][b]คำชี้แจง[/b][br][/u]1.ให้นักเรียนเลือกปุ่ม วงกลม พาราโบลา วงรี หรือ ไฮเพอร์โบลา เพื่อพิิจารณาส่วนโค้งที่ได้จากการตัดพื้นผิวกรวยกลมด้วยระนาบแบน[br]2.ปรับแถบเลื่อน ได้แก่ [br]- เลื่อนระนาบขึ้นและลง[br]- ปรับความชันของระนาบ[br]- เลื่อนระนาบซ้ายและขวา [br]เพื่อสังเกตระนาบตัดผิวกรวยกลม[br]3. บันทึกผล และตอบคำถาม
กำเนิดภาคตัดกรวย ด้วยโปรแกรม Geogebra
1.จากการสังเกตเมื่อระนาบตัดกรวย ใน[b][color=#cc0000]แนวขนานกับฐานของกรวย หรือ แนวตั้งฉากกับแกนของกรวย[/color][/b] จะเกิดภาคตัดกรวยชนิดใด[br]
2.จากการสังเกตเมื่อระนาบตัดกรวย ใน[b][color=#cc0000]แนวที่ไม่ขนานกับกับฐานของกรวยแต่ยังไม่เอียงจนตัดไปถึงฐานกรวย[/color][/b] จะเกิดภาคตัดกรวยชนิดใด[br]
3.จากการสังเกตเมื่อระนาบตัดกรวย ใน[b][color=#900000]แนวที่ไม่ขนานกับกับฐานของกรวยและเอียงจนตัดฐานกรวยหนึ่ง[/color][/b] จะเกิดภาคตัดกรวยชนิดใด[br]
4.จากการสังเกตเมื่อระนาบตัดกรวย ใน[b][color=#cc0000]แนวตั้งฉากกับฐานของกรวยและเอียงจนตัดฐานกรวยหนึ่ง[/color][/b] จะเกิดภาคตัดกรวยชนิดใด[br]
5. เมื่อระนาบตัดกับทรงกรวยกลมในลักษณะที่[b][color=#900000]ผ่านจุดยอดของทรงกรวย[/color][/b] จะเกิดภาคตัดกรวยชนิดใด
กำเนิดพาราโบลา
บทนิยามของพาราโบลา
[b]พาราโบลา [/b][b](parabola) [/b] คือเซตของจุดทั้งหมดในระนาบซึ่งห่างจากจุดที่ตรึงอยู่กับ F ที่จุดหนึ่ง [br]และเส้นตรง d ที่ตรึงอยู่กับที่เส้นหนึ่งเป็น[u][b]ระยะทางเท่ากัน[/b][/u] [br]จุดที่ตรึงอยู่กับที่นี้ เรียกว่า [color=#ff0000][b]โฟกัส[/b][b] (focus)[/b] [/color] [br]และเส้นตรงที่ตรึงอยู่กับที่นี้ เรียกว่า [b][color=#0000ff]เส้นบังคับ[/color][/b] หรือ [color=#0000ff][b]ไดเรกตริกซ์[/b] [/color][b][color=#0000ff](directrix)[/color] [/b]ของพาราโบลา
[u][b][code][/code]คำชี้แจ้ง[/b][/u] ให้นักเรียน[br]1. สร้างจุด C[icon]/images/ggb/toolbar/mode_pointonobject.png[/icon] ซึ่งอยู่บนเส้นตรง d[br]2. สร้างส่วนของเส้นตรง CF [icon]/images/ggb/toolbar/mode_segment.png[/icon][br]3. สร้างเส้นตรงแบ่งครึ่งและตั้งฉาก [icon]/images/ggb/toolbar/mode_linebisector.png[/icon]กับส่วนของเส้นตรง CF [br]4. สร้างเส้นตรง [icon]/images/ggb/toolbar/mode_orthogonal.png[/icon] ที่ผ่านจุด C และตั้งฉากกับเส้นตรง d [br]5. สร้างจุดตัด [icon]/images/ggb/toolbar/mode_intersect.png[/icon]ของเส้นที่คุณสร้างในข้อ 3 และข้อ 4[br]6. คลิกขวาที่จุดตัดในข้อ 5 และเลือก “แสดงรอย" (Trace On)
การสร้างพาราโบลาโดยนิยาม ด้วยโปรแกรม Geogebra
[u][b]คำชี้แจ้ง[/b][/u] ให้นักเรียน[br]1. เลื่อนแถบเลื่อน และเลื่อนจุด P[br]2. พิจารณาระยะห่างระหว่างจุด P กับ จุดโฟกัส [br]และระยะห่างระหว่างจุด P กับไดเรกตริกซ์[br]3. ศึกษาความสัมพันธ์ในข้อ 2 และตอบคำถาม
พาราโบลา
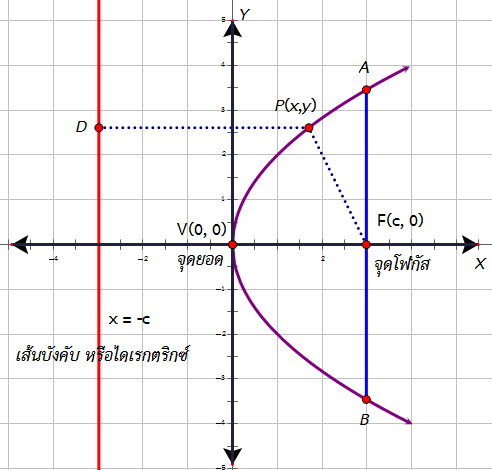
ส่วนประกอบของพาราโบลา
1. เส้นตรงคงที่เรียกว่า [b][color=#ff0000]ไดเรกตริกซ์ [/color][/b]ของพาราโบลา จากรูปคือ เส้นตรง [math]x=-c[/math][br]2. จุดคงที่เรียกว่า [color=#ff0000][b]โฟกัส[/b] [/color]ของพาราโบลา จากรูปคือ จุด [math]F\left(c,0\right)[/math][br]3. เส้นตรงที่ผ่านโฟกัสและตั้งฉากกับไดเรกตริกซ์เรียกว่า [b][color=#ff0000]แกนสมมาตร[/color] [/b]ของพาราโบลา จากรูปคือ แกน [math]x[/math][br]4. จุดที่พาราโบลาตัดกับแกนของพาราโบลาเรียกว่า [b][color=#ff0000]จุดยอด[/color] [/b]ของพาราโบลา จากรูปคือ จุด [math]V\left(0,0\right)[/math][br]5. ส่วนของเส้นตรงที่ตัดพาราโบลาโดยผ่านโฟกัสขนานกับไดเรกตริกซ์ [br]และตั้งฉากกับแกนสมมาตร เรียกว่า [b][color=#ff0000]เลตัสเรกตัม[/color] [/b][b](latus rectum)[/b] จากรูปคือ ส่วนของเส้นตรง [math]AB[/math] จะได้ความยาวของเลตัสเรกตัมเท่ากับ [math]\mid4c\mid[/math]
1.จากการสร้างพาราโบลาโดยนิยาม ด้วยโปรแกรม Geogebra จุดที่ได้จากการตัดกันของเส้นแบ่งครึ่งและเส้นตั้งฉากที่ผ่านจุด C คืออะไร
2.จากการสร้างพาราโบลาโดยนิยาม ด้วยโปรแกรม Geogebra เมื่อเลื่อนจุดบนเส้นตรง d แล้วรอยที่เกิดจากจุดตัดจะเป็นรูปอะไร
3.จุดยอด (vertex) ของพาราโบลาคืออะไร
4.ในการสร้างพาราโบลาด้วย GeoGebra ควรเริ่มจากขั้นตอนใดก่อน
5.จากการสร้างพาราโบลาโดยนิยาม ด้วยโปรแกรม Geogebra จุด C อยู่บนเส้นใด
กำเนิดวงรี
บทนิยามของวงรี
[color=#0000ff][b]วงรี [/b][b](ellipse)[/b][/color] คือเซตของจุดทั้งหมดในระนาบซึ่งผลบวกของระยะทางจากจุดใดๆ[br]ไปยังจุด [math]F_1[/math] และ [math]F_2[/math] ที่ตรึงอยู่กับที่มีค่าคงตัว โดยค่าคงตัวนี้มีค่ามากกว่าระยะห่างระหว่างจุดที่ตรึงอยู่กับที่ทั้งสองจุดสองจุดที่ตรึงอยู่กับที่นี้เรียกว่า [color=#ff0000][b]โฟกัส [/b][b](focus)[/b][/color] ของวงรี
[u][code][/code]คำชี้แจ้ง[/u] ให้นักเรียน[br]1. เลื่อนจุด [math]F_1[/math] หรือ [math]F_2[/math] เพื่อปรับขนาดของวงรี[br]2. เลื่อนจุด [math]P[/math] แล้วสังเกตค่าของ [math]PF_1+PF_2[/math][br]3. พิจารณาความสัมพันธ์ของ [math]PF_1+PF_2[/math] และตอบคำถาม
การสร้างวงรี ด้วยโปรแกรม Geogebra
ส่วนประกอบของวงรี
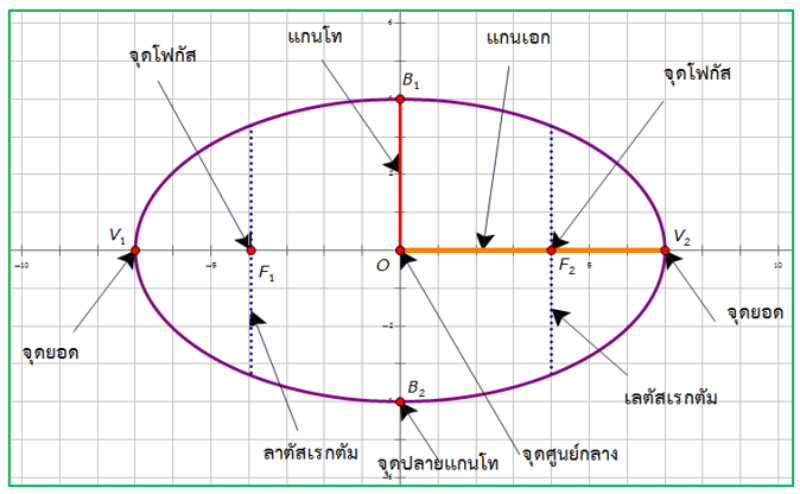
1. O เป็นจุดกึ่งกลางระหว่างโฟกัสทั้งสอง เรียกว่า [b][color=#ff0000]จุดศูนย์กลางของวงรี[/color][/b][br]2. V[sub]1[/sub] และ V[sub]2[/sub] เป็นจุดที่เส้นตรงลากผ่านโฟกัสทั้งสองตัดกับวงรี เรียกว่า [b][color=#ff0000]จุดยอด[/color][/b] ของวงรี[br]3. OV[sub]2[/sub] คือส่วนเส้นตรงที่เชื่อมระหว่างจุดยอดเรียกว่า [b][color=#ff0000]แกนเอก[/color][/b] ของวงรี[br]4. OB[sub]1[/sub] คือส่วนของเส้นตรงที่ตั้งฉากกับแกนเอกที่จุดศูนย์กลาง และมีจุดปลายอยู่บนวงรีทั้งสองด้าน เรียกว่า [b][color=#ff0000]แกนโท[/color][/b] ของวงรี[br]5. ส่วนของเส้นตรงที่ตั้งฉาก กับแกนเอก ที่โฟกัส และมีจุดปลายทั้งสองด้านบนวงรี เรียกว่า [b][color=#ff0000]เลตัสเรกตัม[/color] [/b]ของวงรี
1.วงรีคือเซตของจุดในระนาบที่มีคุณสมบัติใด
2.จุดที่ตรึงอยู่กับที่ทั้งสองในนิยามของวงรีเรียกว่าอะไร
3.วงรีมีจุดศูนย์กลาง (center) อยู่ที่ใด
4.จากกิจกรรม GeoGebra เมื่อเลื่อนจุด P ไปตามเส้นวงรี จะเกิดอะไรขึ้นกับ [math]PF_1+PF_2[/math]
5.ถ้าเลื่อนจุดโฟกัสให้ใกล้ศูนย์กลางมากขึ้น วงรีจะมีลักษณะอย่างไร
กำเนิดไฮเพอร์โบลา
บทนิยามของไฮเพอร์โบลา
[color=#0000ff][b]ไฮเพอร์โบลา[/b] (hyperbola)[/color] คือเซตของจุดทั้งหมดในระนาบซึ่ง [b][color=#ff0000]ผลต่าง[/color][/b]ของระยะทางจากจุดใดๆ ไปยังจุด F[sub]1[/sub][br]และ F[sub]2[/sub] ที่ตรึงอยู่กับที่ มีค่าคงตัว โดยค่าคงตัวน้อยกว่าระยะห่างระหว่างจุดคงที่ที่ตรึงอยู่กับที่ทั้งสอง[br]จุด F[sub]1[/sub] และ F[sub]2[/sub] ดังกล่าวนี้ เรียกว่า [b][color=#ff0000]โฟกัส[/color] [/b]ของไฮเพอร์โบลา[br]
กำเนิดไฮเพอร์โบลา ด้วยโปรแกรม Geogebra
บทนิยามของไฮเพอร์โบลา
1.ไฮเพอร์โบลา คือเซตของจุดทั้งหมดในระนาบที่
2.จุดคงที่สองจุดในนิยามของไฮเพอร์โบลามีชื่อเรียกว่า
3.จุดศูนย์กลางของไฮเพอร์โบลาคือจุดใด
4.ไฮเพอร์โบลามีเส้นกำกับทั้งหมดกี่เส้น
5.จุดโฟกัสของไฮเพอร์โบลาตั้งอยู่ที่
ตอนที่ 1 แบบทดสอบแบบปรนัย
[b]แบบทดสอบวัดผลสัมฤทธิ์ทางการเรียน (หลังเรียน)[br]คำชี้แจง ให้นักเรียนเลือกคำตอบที่ถูกต้องที่สุด [/b]
1. ให้ [math]x^2+y^2-16x-16y+64=0[/math] จัดรูปเป็นสมการวงกลมมาตรฐานตามข้อใด
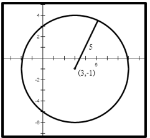
2.จากรูปด้านบน วงกลมต่อไปนี้ตรงกับสมการใด
3.สมการของวงกลมที่มีจุดศูนย์กลางอยู่ที่จุด [math]\left(-4,2\right)[/math] และสัมผัสกับเส้นตรง [math]3x-4y+40=0[/math] คือสมการในข้อใด[br][br]
4.กราฟของสมการ [math]x^2+y^2-6x+2y-15=0[/math] เป็นวงกลมหรือไม่ ถ้าเป็นจุดศูนย์กลางและรัศมีมีค่าเท่าใด [br][br]
5.จงหาจุดศูนย์กลางและรัศมีของ [math]2x^2+2y^2-3x+4y+3=0[/math]
6.ข้อใดคือสมการของพาราโบลาที่มีไดเรกตริกซ์คือเส้นตรง [math]x=12[/math] และโฟกัสที่จุด (2,0)
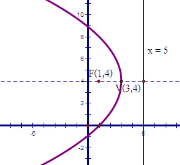
7.จากรูป กราฟพาราโบลาต่อไปนี้ตรงกับสมการใด
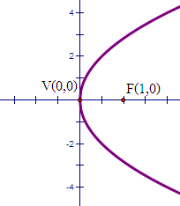
8.จากรูป กราฟพาราโบลาต่อไปนี้ตรงกับสมการใด
9.จากสมการ [math]y^2-12x=0[/math] จุดยอด และจุดโฟกัส ของพาราโบลาตรงกับข้อใด
10. พาราโบลามีจุดยอดอยู่ที่จุด (-2,-6) และโฟกัสอยู่ที่จุด (-2,-2) สมการไดเรกตริกซ์ตรงกับข้อใด[br][br]
11.วงรีที่มีจุด (4,0) และ (–4,0) เป็นจุดยอด มีโฟกัสจุดหนึ่งอยู่ที่ (3,0) จะมีสมการตรงกับข้อใด
12.กำหนดสมการวงรี [math]\left(\frac{y}{9}\right)^2+\left(\frac{x}{4}\right)^2=1[/math] จุดยอดคือข้อใด
13. กำหนดสมการ [math]\frac{y^2}{144}+\frac{x^2}{25}=1[/math] ข้อใดสรุป[b][u]ถูกต้อง[/u][/b][br]
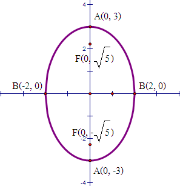
14. จากรูปกราฟวงรีต่อไปนี้ตรงกับสมการใด[br][br]
15. กำหนดสมการวงรี [math]\frac{\left(x-2\right)^2}{100}+\frac{\left(y-1\right)^2}{25}=1[/math] จุดยอดคือข้อใด[br]
16.กำหนดสมการไฮเพอร์โบลา [math]\frac{x^2}{16}-\frac{y^2}{4}=1[/math] จุดยอดคือข้อใด[br]
17. ข้อใดคือจุดโฟกัสของสมการไฮเพอร์โบลา [math]\frac{x^2}{9}-\frac{y^2}{4}=1[/math]
18. ไฮเพอร์โบลาที่มีจุดยอดที่จุด (5,0) กับจุด (-5,0) มีจุดโพกัสยอดหนึ่งที่จุด (-6,0) มีจุดศูนย์กลางที่จุดใด[br][br]
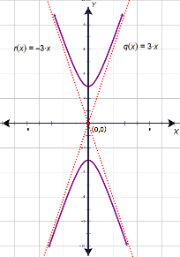
19. จากรูปกราฟไฮเพอร์โบลาต่อไปนี้ตรงกับสมการใด[br][br]
20. ไฮเพอร์โบลาซึ่งมีโฟกัสอยู่ที่ (5, 0) และ (-5, 0) มีแกนตามขวางยาว 8 หน่วย มีสมการตรงกับข้อใด[br][br]