Planul lecției: Proprietăți în triunghiul dreptunghic
Informații despre lecții
[list][*]Subiect: Matematică[br][/*][*]Nivelul clasei: 6[/*][*]Durata: 50 '[/*][*]Mijloace TIC: calculatorul profesorilor cu proiector, calculatoarele studențești (sau tablete sau smartphone-uri[i])[/i][/*][/list]
Tema
Descoperirea și învățarea unor proprietăți ale triunghiului dreptunghic, teorema medianei pe ipotenuză și teorema unghiului de 30 de grade.
Rezultatele învățării
După terminarea lecției, elevii vor:[br][list][*]ști că în orice triunghi dreptunghic, mediana pe ipotenuză măsoară o jumătate din ipotenuză;[br][/*][*]ști și explica de ce într-un triunghi dreptunghic, cateta opusă unghiului de 30 măsoară o jumătate din ipotenuză;[br][/*][*]să poată calcula unele elemente necunoscute ale unui triunghi dreptunghic atunci când sunt date ipotenuza sau mediana corespunzătoare ipotenuzei.[/*][/list]
Obiective operaționale și evaluarea
[u]Obiectivele lecției[/u][br][br]Până la sfârșitul lecției, elevii vor fi capabili să:[list][*]să indice și să explice că mediana pe ipotenuză împarte triunghiul dreptunghic în două triunghiuri isoscele, independent de măsurile sau poziția triunghiului dreptunghic;[/*][*]să concluzioneze și să aplice faptul că lungimea medianei pe ipotenuză măsoară jumătate din ipotenuză;[/*][*]să concluzioneze și să rețină că, atunci când un unghi al triunghiului dreptunghic măsoară 30 grade, cateta care i se opune măsoară jumătate din ipotenuză;[/*][*]calculeze elementul necunoscut, ipotenuza, jumătate din hypotenuse, mediana pe ipotenuză, cateta opusă unghiului de grade, etc., atunci când celelalte sunt date.[/*][/list][u]Evaluare[br][/u][list][*]Discuții și verificarea finalizării fișei de lucru interactive 2;[/*][*]Verificarea temelor după lecție. [/*][/list]
Strategii de predare
[u]Strategiiși metode: [br][/u][list][*]Metodele de investigare, folosind modele de hârtie triunghiulare și modelare asistată de tehnologie se vor combina cu dialogul euristic și / sau structurat;[/*][*]Tehnologia va contribui la aproximativ jumătate din lecție, în special datorită exercițiilor oferite de Fișa de lucru interactivă 2.[/*][/list][br][u]Momente și activități:[br][br][/u]1) Moment introductiv (2')[br][br]Profesorul va primi studenții și va oferi informații despre temă și va anunța utilizarea noilor tehnologii în timpul lecției.[br][br][u]2) Recapitulare (5')[br][br]Elevii vor fi invitați să discute despre:[/u][br][list][*]proprietățile principale ale triunghiului isoscel și ale triunghiului echilateral;[/*][*]definiția și proprietățile liniei mijlocii.[/*][/list][br][u]3) Învățarea prin descoperire (15 ')[/u] [br][br]Elevii vor manipula modelele de hârtie și aplicațiile GeoGebra, pentru a descoperi teorema medianei pe ipotenuză și teorema unghiului de 30 de grade. Fiecare elev va avea acces la un pachet de triunghiuri de hârtie (după cum puteți vedea în paragraful Resurse) și la un dispozitiv digital cu conexiune la Internet și / sau GeoGebra.[br][br][u]Investigarea prin plierea modelelor de hârtie:[br][/u][br][list][*]Luați triunghiul dreptunghic (cel mai mare) și să presupunem că vârful unghiului drept este A, iar celelalte, sunt B și C. Alegeți vârful A cu mâna și vârful B cu cealaltă mână și pliați hârtia astfel încât vârful B să se suprapună peste vârful A. Apăsați ușor hârtia până când devine plată. Apoi faceți același lucru cu vârful C și ar trebui să obțineți o hârtie de formă dreptunghiulară. Apoi pliați dreptunghiul în două părți egale, pe diagonala formată în acest proces. Acum, puteți deschide hârtia și observați-o.[/*][*]Îndoiți și derulați modelul și colorați liniile rezultate în proces, ce reprezintă liniile? Notați triunghiul, numele segmentelor importante observate. Se așteaptă ca studenții să observe că cele două jumătăți ale ipotenuzei și medianei pe ipotenuză, se suprapun în proces, deci au aceeași lungime. [/*][*]Întrebare: Cum sunt triunghiurile formate de mediana pe ipotenuză, cu cele două jumătăți ale ipotenuzei? Acestea sunt isoscele și cum putem dovedi asta? [/*][*]Întrebare: După colorarrea liniilor mijlocii, întrebăm, de ce sunt linii mijlocii? [/*][*]Întrebare: Fiecare linie mijlocie este o mediană pentru fiecare triunghi format de mediana pe ipotenuză, nu ar și înălțime? Da, deoarece aceste triunghiuri sunt isoscele.[/*][*]Luați triunghiul echilateral și jumătățile sale, triunghiurile mici și încercați să le suprapuneți.[/*][*]Întrebare: Cum sunt unghiurile măsurii triunghiului echilateral (așteptăm 60)? Deci, cum se măsoară unghiurile acute ale celor două triunghiuri drepte (30 și 60[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAoAAAAPCAYAAADd/14OAAAAV0lEQVQoU2NkIBIwEqmOAV3hBAYGhg8MDAwPGBgYFiAbgqwwgYGBYQNUoQIDAwMIH4ApRlYYwMDAcAFqmgNUA4gPBuhWg0wVgCrCaTVef5Hta5ymjkwTAUsaDBArM3svAAAAAElFTkSuQmCC[/img])? [/*][*]Ce puteți spune despre catete și despre ipotenuză din triunghiurile dreptunghice? [/*][*]Întrebare: Putem presupune că tot ceea ce am observat și învățat despre aceste modele de hârtie va fi valabil pentru orice alte triunghiuri dreptunghice? [/*][*]Tehnologia ne va ajuta să răspundem la acestă întrebare.[/*][/list][u][br]Investigarea prin utilizarea foilor de lucru interactive GeoGebra:[br][br][/u]Elevii vor deschide Fișa de lucru interactivă 1 și vor verifica proprietățile schimbând dimensiunile și poziția triunghiului drept. Ei vor folosi butoanele pentru a vizualiza mediana, și liniile mijlocii.[br][list][*]Cum sunt lungimile ipotenuzei și a medianei? Sau cateta opusă unghiului de 30 de grade?[/*][*]Întrebare: Congruența depinde de poziția sau măsurarea triunghiurilor drepte (nu!)?[/*][*]Întrebare: Cum se poate explica diferența când se observă (discutați aproximația)?[/*][*]Ce putem încheia?[/*][/list][br][u]4) Argumentarea și scrierea demonstrației (15'):[/u][br][br]Elevii vor fi invitați să raporteze și să scrie dovezile logice sub supravegherea profesorilor. Se vor dovedi următoarele trei rezultate:[br][list][*]Lema: mediana ipotenuzei și cele două jumătăți ale ipotenuzei determină două triunghiuri isoscele (de exemplu, dovedind că liniile mijlocii sunt și mediane și înălțimi în același timp);[/*][*]Teorema 1: mediana corespunzătoare ipotenuzei măsoară o jumătate de ipotenuză, în orice triunghi dreptunghic;[/*][*]Teorema 2:Cateta care se opune unghiului de 30 ° măsoară o jumătate de ipotenuză.[/*][/list][br][u]5)Consolidarea cunoștințelor (10')[/u][br]Elevii vor deschide fișa Interactivă 2 și vor rezolva exercițiile, care se generează în mod dinamic. Mai multe exerciții pot fi obținute prin deplasarea vârfurilor triunghiului dinamic.[br][br]6) Solicitarea de feedback și tema acasă (3'). [br][br]Ca temă suplimentară, alături de câteva exerciții oferite în manualele de matematică, elevii vor trebui să construiască un puzzle de hârtie, folosind cele două triunghiuri mari, de diferite culori. Acestea vor fi tăiate în patru triunghiuri congruente, ele vor fi asemenea cu cele mai mari. Apoi, fiecare triunghi mic va fi îndoit ca mai sus și tăiat în alte patru triunghiuri, iar procesul poate fi repetat. Jocul va fi de a reconstitui un triunghi mare folosind triunghiurile mici colorate diferite.
Resurse
Triunghiurile model de hârtie:[br]Fiecare elev va primi de preferință două triunghiuri de hârtie drepte de diferite culori, un triunghi echilateral împreună cu două triunghiuri drepte cu 30 de unghi (fiind exact jumătățile unui triunghi echilateral). Un pachet pentru un elev ar putea fi produs folosind două foi A4 de hârtie de diferite culori: [url=https://ggbm.at/EbCRpSSN]https://ggbm.at/EbCRpSSN[/url][br]Fișa interactivă 1: Explorați triunghiul dreptunghic:[br][br]Foaie de lucru interactivă 2 "Median pe hipotensie - exerciții": https://ggbm.at/hbpvzeur
Integrarea noilor tehnologii
[list][*]Elevii au nevoie doar de câteva explicații scurte pentru a utiliza foile de lucru interactive și nu au nevoie de cunoștințe anterioare pentru a folosi în mod adecvat tehnologia în timpul lecției.[/*][*] În mod ideal, vom utiliza rețeaua de internet, un calculator pentru profesori și un proiector, precum și calculatoarele studenților (sau tablete sau smartphone-uri) cu toate acestea, ar trebui să descărcăm foile de lucru, pentru cazul în care rețeaua nu funcționează;[/*][*]Lecția poate continua fără nici o tehnologie (folosind numai modelele de hârtie pregătite anterior), dar mai lent, astfel încât poate lua în considerare o durată mai lungă, pentru ca elevii să facă desene și măsurători suplimentare.[/*][/list]
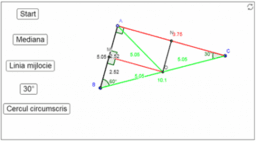
Mediana corespunzătoare ipotenuzei
Reflecții după lecție - Proprietăți în triunghiul dreptunghic
How did you implement your lesson plan?
Am implementat lecțiile de mai multe ori. A trebuit să fie adaptată funcție de nivelul matematicii studenților. Elevii care nu au dezvoltat încă logica formală sau cei care învață încet vor beneficia mai mult de momentele practice și nu ar putea să acorde atenție atunci când vor fi scrise dovezi formale. Profesorul trebuie să găsească echilibrul corect între practică și formală, astfel încât să stimuleze dezvoltarea gândirii logice fără a sacrifica orice timp al elevilor.
Have you integrated technology well?
Lecția a fost mai ușor de realizat în laboratorul TIC, cu toate acestea, a lucrat în clasă obișnuită, folosind un laptop profesor și telefoane smartphone-uri ale studenților. Desigur, foile de lucru interactive au fost pregătite, iar modelele de hârtie.
Did your students reach the objectives of the lesson?
Da, după cum știu, au fost atinse cel puțin obiectivele minime.
What do students say about the lesson?
Ei au apreciat foarte mult ancheta folosind modele de hârtie, precum și tehnologia.
What could be improved to make your method work better?
[i]I would like to have an easier access in the ICT lab or have digital devices in every classroom.[/i]