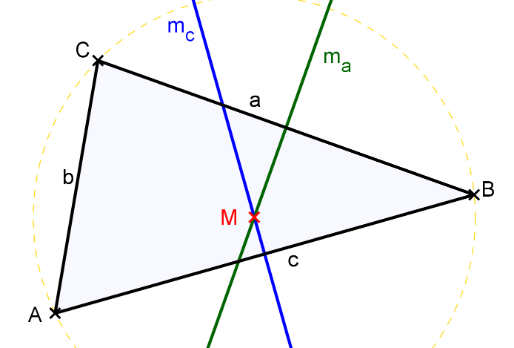
Der Schnittpunkt der Mittelsenkrechten heißt M.[br][br]Behauptung: M liegt auf allen drei Mittelsenkrechten.[br][br][br]Jeder Punkt auf der Mittelsenkrechten m[sub]c [/sub] ist gleich weit von A und von B entfernt => [math]\left| \overline {MA}\right|=\left| \overline {MB}\right|[/math] (I)[br] [br]Jeder Punkt auf der Mittelsenkrechten m[sub]a [/sub] ist gleich weit von B und von C entfernt =>[math]\left| \overline {MB}\right|=\left| \overline {MC}\right|[/math] (II)[br][br]aus (I) und (II) => [math]\left| \overline {MA}\right|=\left| \overline {MC}\right|[/math] *[br][br][br][br][br][i]Bemerkung[br][/i][i]Bis hierher: zwei Geraden schneiden sich in einem Punkt → M[/i][br][i]aber die Frage ist: liegt M auch auf m[sub]b[/sub] ?[/i][br][br][br]Wegen der Umkehrung aus * => M ist von A und C gleich weit entfernt => M liegt auf [i]m[sub]b[/sub] [/i][br][br][br]