Priručnik: 3D kalkulator
Dobrodošli u [url=https://www.geogebra.org/3d]GeoGebra 3D Calculator[/url]! Naučite kako crtati tijela, vizualizirati rotacije i sjecišta s 3D, istražite objekte proširenom stvarnošću, i mnogo drugih stvari s ovim priručnikom. [b]Prijevod: [/b]Josip Kličinović, 30.11.2020.
Table of Contents
- Prvi koraci
- Usporedba GeoGebrinih aplikacija
- Uvod
- Istraži aplikaciju
- Algebra
- Alati
- 3D grafički prikaz
- Proširena stvarnost - Augmented Reality (AR)
- Osnovno
- Valjak i kocka
- Modeliranje u proširenoj stvarnosti
- Rotacije
- Presjek stošca i ravnine
- Kružnice u 3D
- Napredno
- Sferni trokuti
- Plohe drugog reda
- Poliedri i zrcaljenje
- YouTube priručnici
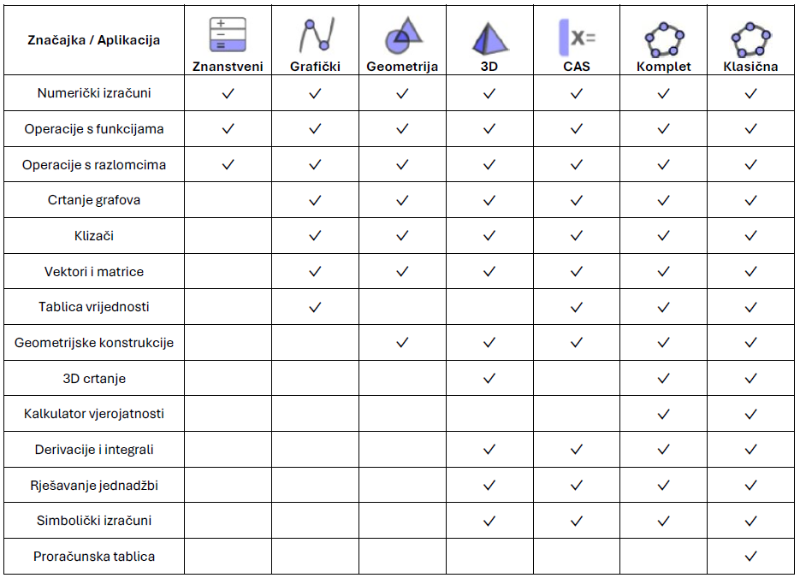
Usporedba GeoGebrinih aplikacija
S našim novim GeoGebrinim aplikacijama možete istraživati i učiti o funkcijama, geometriji, algebri, statistici i 3D na nov i interaktivan način.[br][br][list][*][url=http://www.geogebra.org/scientific]Znanstveni kalkulator[/url][br][/*][*][url=https://www.geogebra.org/graphing]Grafički kalkulator[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometrija[/url][br][/*][*][url=https://www.geogebra.org/calculator]Komplet kalkulatora[/url][/*][*][url=https://www.geogebra.org/cas]CAS Kalkulator[/url][br][/*][*][url=https://www.geogebra.org/3d]3D Kalkulator[/url][/*][*][url=https://www.geogebra.org/classic]Klasična GeoGebra[/url][/*][/list]Prava aplikacija za Vas je ona koja koristi potrebama Vas i Vaših učenika i, ako se koristi u toku ispita, zadovoljava pravnu regulativu države. Sljedeća tablica daje pregled koje su značajke dostupne u pojedinoj aplikaciji.
GeoGebra na ispitu
Čvrsto vjerujemo da će učenici profitirati od od korištenja točno one GeoGebrine aplikacie koju koriste u učionici, kod kuće, i tijekom ispita. Na taj će način dobiti najviše iskustva u radu s aplikacijom te će stoga na najbolji mogući način iskoristiti tehnologiju na pravi način u svim situacijama. Zbog toga smo izradili [url=https://www.geogebra.org/m/nauqds9v]ispitni način rada[/url] koji smo dodali u svaku našu aplikaciju. Ispitni način zaključava uređaj kako učenici ne bi mogli komunicirati s nekim ili koristiti neke druge aplikacije tijekom ispita. Ovaj je način već isproban u školama i odobren od strane nekoliko ministarstava nadležnih za obrazovanje. Pročitajte više o tome u priručniku [url=https://www.geogebra.org/m/nauqds9v]GeoGebra na ispitu[/url].[br][br]
Valjak i kocka
Zadatak
Napravite valjak i kocku[br][br]Pogledajte video (na engleskom) i proučite kako se bapravi valjak i kocka koristeći [i][url=https://www.geogebra.org/3d]GeoGebra 3D Calculator[/url][/i]. Potom isto pokušajte sami prateći upute koje se nalaze ispod videa.
Pogledajte video (na engleskom jeziku)
Upute
[table][tr][td]1. [/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Otvorite [i]Postavke[/i] i odaberite [i]Pokaži mrežu[/i][/td][/tr][tr][td]2.[/td][td][/td][td]U [i]Algebri[/i] unesite naredbu [math]Valjak((2,-3,-1),(2,2,2),2)[/math] kako biste izradili valjak kroz dvije točke i duljine polumjera 2. Pritisnite [i]Enter.[/i][/td][/tr][tr][td]3.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Istražite različite [i]Projekcije [/i]mijenjajući ih u [i]Postavama.[/i][/td][/tr][tr][td]4.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_point.png[/icon][/td][td]Otvorite [i]Alate,[/i] odaberite alat [i]Točka[/i] i izradite dvije točke[/td][/tr][tr][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_cube.png[/icon][/td][td]Odaberite alat [i]Kocka, [/i]a potom odaberite izrađene točke kako bi konstruirali kocku[/td][/tr][tr][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Odaberite [i]Pomicanje [/i]kako bi istražili konstrukciju[br][/td][/tr][/table]
Pokušajte sami...
Proširena stvarnost
Ako koristite [i]GeoGebra 3D kalkulator [/i]na svom mobilnom uređaju, prebacite se u način rad [i]AR [/i]kako biste izrađene matematičke objekte postavili na neku plohu (npr, na stol, pod...) kako biste hodali oko njih i istražili ih. Istražite svoju konstrukcije iz nove perspektive!
Sferni trokuti
Zadatak
Izradite trokut na sferi.[br][br]Pogledajte video (na engleskom jeziku) i izradite trokut na sferi koristeći [i][url=https://www.geogebra.org/3d]GeoGebra 3D kalkulator[/url][/i]. Potom pokušajte to sami napraviti slijedeći upute ispod videa.
Pogledajte video (na engleskom jeziku)
Upute
[table][tr][td]1.[/td][td][/td][td]U [i]polje za unos Algebre[/i] unesite [math]A=(0,0,0)[/math] i naredbu [math]Sfera(A,1)[/math].[/td][/tr][tr][td]2.[/td][td][/td][td]Odaberite sferu u [i]3D grafičkom prikazu, [/i]a potom odaberite [img]https://wiki.geogebra.org/uploads/thumb/d/d5/Color_button.svg/16px-Color_button.svg.png[/img] kako biste promijenili boju sfere.[br][/td][/tr][tr][td]3.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]U postavkama odznačite [i]Pokaži osi[/i] i [i]Pokaži ravninu[/i] kako biste sakrili osi i ravninu.[/td][/tr][tr][td]4.[/td][td][/td][td]Odaberite [i]Alate[/i].[/td][/tr][tr][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_point.png[/icon][/td][td]Odaberite alat [i]Točka[/i] i izradite tri točke [i]B, C, [/i]i[i] D[/i] na sferi.[/td][/tr][tr][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_circlearc3.png[/icon][/td][td]Odaberite alat [i]Kružni luk[/i] te prvo odaberite središte [i]A[/i], a potom točke [i]B[/i] i [i]C[/i]. Istu stvar napravite s preostalim točkama kako biste izradili sferni trokut. Uvijek počnite od točka [i]A[/i].[br][/td][/tr][tr][td]7.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Odaberite alat [i]Pomicanje [/i]i pomičite točke po sferi kako biste istražili konstrukciju.[br][/td][/tr][/table]
Pokušajte sami...
Proširena stvarnost
Ako koristite [i]GeoGebra 3D kalkulator [/i]na svom mobilnom uređaju, prebacite se u način rad [i]AR [/i]kako biste izrađene matematičke objekte postavili na neku plohu (npr., na stol, pod...) kako biste hodali oko njih i istražili ih. Istražite svoju konstrukcije iz nove perspektive!