Geometry
Inhaltsverzeichnis
- Plotting Points
- Plotting Points Practice
- Plotting Points Homework
- Battleship
- Battleship in the Coordinate Plane!
- Translations
- Translating Shapes Practice
- Translating Shapes Homework
- Reflections
- Reflecting Shapes Practice
- Reflecting Shapes Homework
- Rotations
- Rotating Shapes Practice
- Rotating Shapes Homework
- Similar Shapes & Dilations
- Dilations Tasks
- Dilations Homework
- Tessellations
- Tessellations Practice
- Three-Dimensional Figures
- Three-Dimensional Figures
- Geogebra Practice
- Practicing the Tools
Plotting Points Practice
Identify the coordinates in the graph above (x, y):
On the following graph, plot these points: (3,-2) (-9,-7) (6,10) (4,0) (8,-3) (-10,-10) (7, 6)
Polygon ABCD has vertices A (-6, 1) B (0, 7) C (7, -2) D (0, -8). Use the coordinates of the vertices to draw ABCD
Determine the coordinates of one point inside and one point outside ABCD (from the graph above).
Battleship in the Coordinate Plane!
Creation of this activity was inspired by [url=https://twitter.com/alicekeeler]Alice Keeler[/url]'s blog article "[url=http://www.alicekeeler.com/2016/01/14/game-based-learning-google-slides-coordinate-plane-battleship/]Game Based Learning: Google Slides Coordinate Plane Battleship[/url]".
INTRODUCTION:
[b]This game is played JUST LIKE the old Milton-Bradley game BATTLESHIP. [br]Yet here we'll be playing within the context of the COORDINATE PLANE. [br]The goal is to to SINK ALL 5 of your opponent's ships before he/she sinks all 5 of yours. [/b][br][br][b]When it is YOUR TURN, be sure to state the following: [/b][br][br][b]1) Quadrant Number[br]2) The Ordered Pair[br][br][/b]For example, stating "Quadrant 2: Negative 3 comma 2" indicates the ordered pair (-3, 2). [br]If it's a "MISS", plot a white point on your game board at that location. [br][color=#cc0000]If it's a "HIT", plot a red point on your game board at that location. [br][br][/color]Once you sink one of your opponent's ships, he/she needs to announce this fact to you. [br]When this does happen, use the SEGMENT tool to mark a sunken ship. [b][color=#ff00ff][i]Have fun! [/i][/color][/b]
How to Move Your Ships (at the Beginning); How to Mark Opponent's HITS (RED) and misses (yellow)
How to Plot YOUR OWN HITS (RED) and MISSES (WHITE) & How to Mark a Sunken Ship
YOUR GAME BOARD:
OPPONENT'S GAME BOARD: KEEP TRACK OF YOUR HITS & MISSES HERE.
Translating Shapes Practice
A triangle FGH has vertices at F (-5, 4) G (-4, -3) and H (2, 1). This triangle is translated [-4, 1]. Plot the image of FGH after this translation. (HINT: Drawing the original triangle may help)
Reflecting Shapes Practice
Triangle ABC has vertices A (1, 6), B (8, 2), and C (1, 3). Draw its reflection in the x-axis.
Triangle ABC has vertices A (-8, -4), B (-6, -6), and C (-9, -7). Draw its reflection in the vertical line 5 units to the left of the y-axis.
Describe the reflection that took place.
Describe the reflection that took place from Polygon A to its' image.
What would the new coordinates be if this shape was reflected in the x-axis?
What would the new coordinates be if it was reflected across the line x = 4?
Rotating Shapes Practice
The point A was rotated about the point B to give the image point A'.
A. What is the angle of rotation?[br]B. What is the direction of rotation?
You can use this graph for the following question.
Triangle ABC has vertices A (2, 4), B (7, 4), C (6, 1).[br]Determine the coordinates of the image of triangle ABC after a rotation 90 degrees CCW about the origin.
Parallelogram ABCD has vertices A (1, 3), B (3, 7), C (6, 6), and D (3, 1). Plot the image of ABCD after a 180 degree CCW rotation.
Draw the figure with coordinates A (5, 6), B (6, 7), C (8, 7), and D (8, 5).
Draw the image of the figure above after each transformation. [br]Label each image using the "Pen" option.[br]A) A translation of 6 units right and 2 units down[br]B) A reflection in a vertical line where x = 11[br]C) A rotation of a 45 degree turn clockwise about point D[br]D) A reflection in a horizontal line where y = 4[br]E) A rotation of 90 degrees about point A
Rotate the rectangle 90 degrees CW about C. Rotate the image of the rectangle 180 degrees CCW about A'.
Suppose you rotate a figure 90 degrees CW. [br]A) Name another CW rotation that would give the same rotation image.[br]B) Name a CCW rotation that would gave the same rotation image.
Dilations Tasks
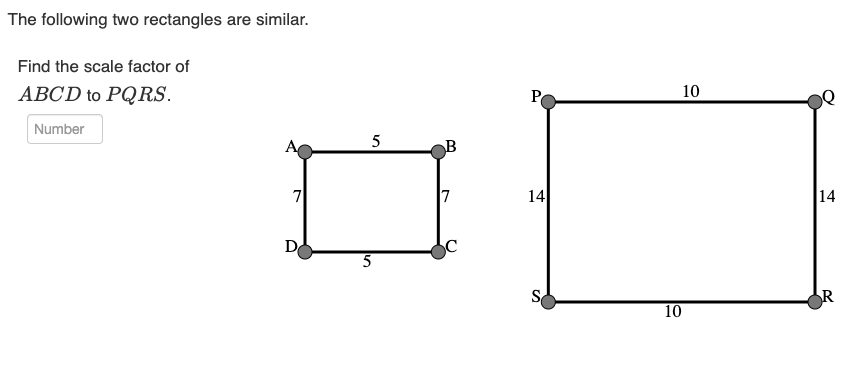
What is the scale factor of ABCD to PQRS?
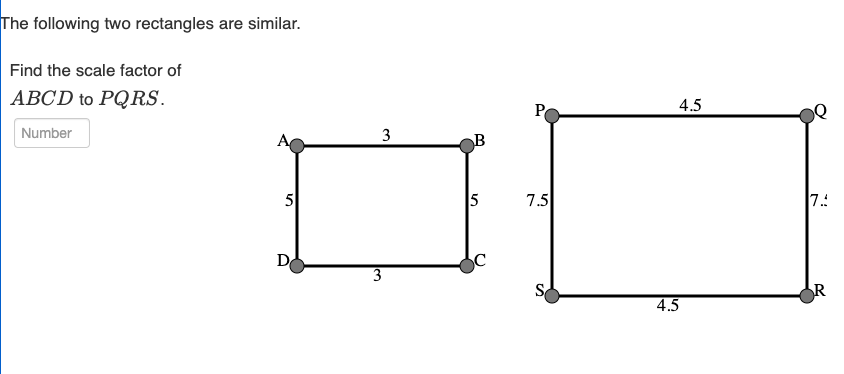
What is the scale factor of ABCD to PQRS?
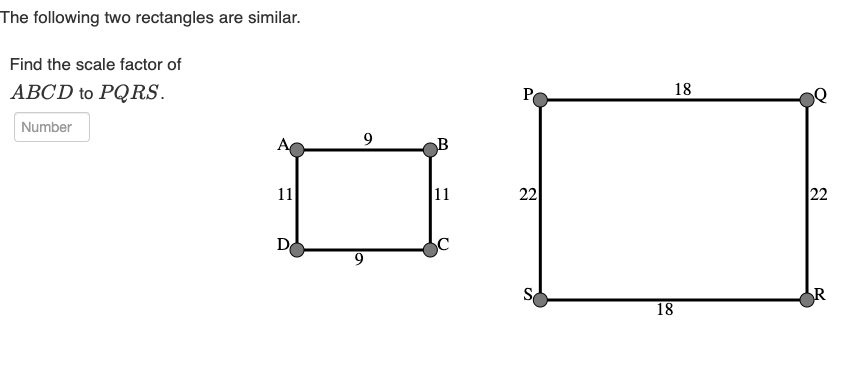
What is the scale factor of ABCD to PQRS?
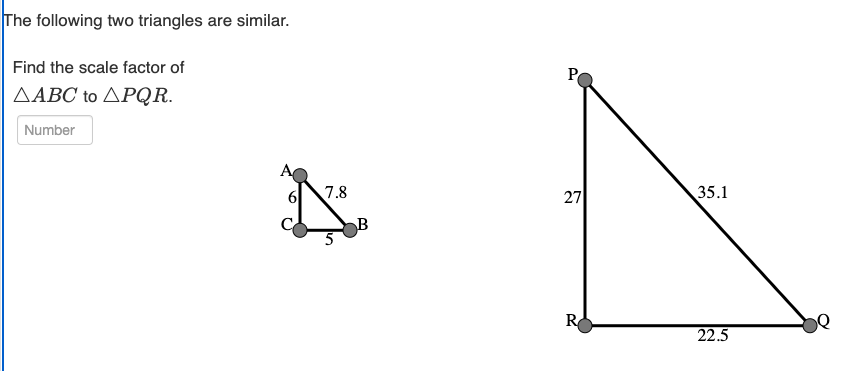
What is the scale factor of ABC to PQR?
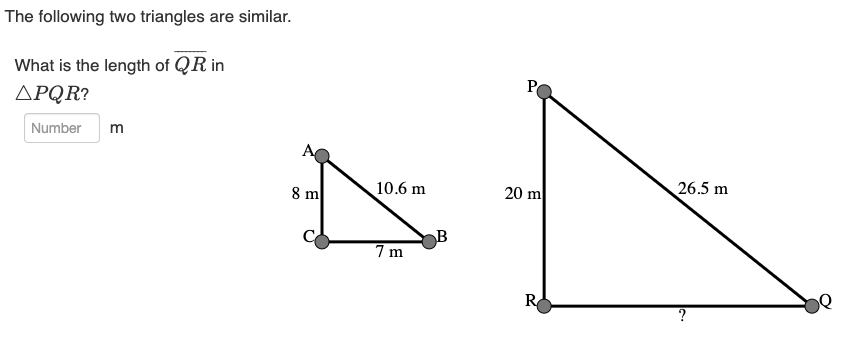
What is the length of QR in PQR?
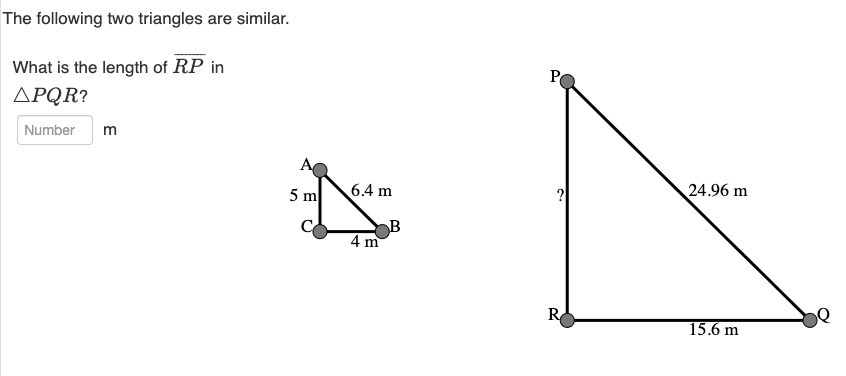
What is the length of RP in PQR?
Tessellations Practice
Is a triangle a tessellating shape?[br]Use the above task to visualize your thinking and support your answer.
Is a rectangle a tessellating shape?[br]Use the above task to visualize your thinking and support your answer.
Is a hexagon a tessellating shape?[br]Use the above task to visualize your thinking and support your answer.
Create a shape that does not tessellate. Show that you have tried tessellating it using the three symmetry rules to prove that it will not
Create a tessellating shape of your own (not a regular polygon) and show that it tessellates by following the three rules of symmetry: translating, rotating, and reflecting.
Three-Dimensional Figures
3D Figures
State the total number of faces on each of the following 3D figures:[br]1. Cube[br]2. Square pyramid[br]3. Rectangular prism[br]4. Triangular pyramid[br]5. Pentagonal prism[br]6. Hexagonal prism[br]7. Pentagonal pyramid[br]8. Hexagonal pyramid[br]9. Triangular prism[br]10. Rectangular pyramid
State the number of rectangular faces on each of the following three-dimensional figures:[br]11. Triangular prism[br]12. Pentagonal prism[br]13. Hexagonal prism[br]14. Triangular pyramid
Name 3 three-dimensional figures that have fewer than 3 edges.
Polyhedras
The shape of each face of a rectangular prism is a(n)...
Faces of a prism or pyramid meet at a(n)...
Edges of a prism or a pyramid meet at a(n)...
What polyhedron has 5 congruent triangles?
What polyhedron has 2 congruent triangles?
What polyhedron has 2 triangles and 3 rectangles?
What polyhedron has 5 pentagons and 5 triangles?
Practicing the Tools
Plotting Points: Make any shape by plotting points over all quadrants.
What are the coordinates of each point you plotted in the above graph?
Translation: Make any shape with 5 sides.
With the shape above, do the following:[br][list][*]Translate your shape 3 times with the Vector Tool[/*][*]Make sure your Image is starting off in quadrant 1[/*][*]Then, your image is being translated into the next two quadrants[/*][*]Record all the proper coordinates (Prime’) and ensure that you are translating it off the Image every time [/*][/list]
Rotation: Make an image with 3 vertices.
Using the graph above, complete the following:[br][list][*]Place your image in the Fourth Quadrant[/*][*]Plot your 4th point at the origin (0,0)[/*][*]Rotate your shape 2 times clockwise 90 and 270 degrees[/*][*]Rotate your shape 2 more times counterclockwise 90 and 270 degrees[/*][/list]
Reflection: Make a hexagon in the 1st quadrant.
Complete the following using the shape above:[br][list][*]Reflect the shape in the X and Y axis[/*][*]Reflect the shape in the horizontal axis 4 units below the x-axis[/*][*]Write down the new coordinates[/*][/list]
Dilation: Make a quadrilateral centered at the origin.
Using the above graph, complete the following:[br][list][*]Dilate the quadrilateral by a scale factor of 3[/*][*]Identify the new coordinates[/*][*]Dilate the quadrilateral by a scale factor of 1/4 [/*][*]Identify the new coordinates[/*][/list]