3. Geometrische und Funktionale Aspekte der Trigonometrie

M.F., Regina Paleczek, Nov 27, 2019

Schritt für Schritt zur allgemeinen Sinusfunktion.

Table of Contents

  1. 3.1 Sinus und Kosinus am Einheitskreis (Wiederholung)
    1. Trigonometrie im rechtwinkligen Dreieck und am Einheitskreis
    2. Sinus, Kosinus, Tangens am Einheitskreis
    3. Wiederholung: Funktion und ihre Darstellungen
  2. 3.2 Vom Einheitskreis zur Sinuskfunktion
    1. Sinus am Riesenrad
    2. Die Entstehung der Sinus- und Kosinusfunktion aus dem Einheitskreis
  3. 3.3 Die allgemeine Sinusfunktion
    1. Wiederholung: Manipulationen von Funktionen
    2. Form und Lageänderung in "y-Richtung"
    3. Form und Lageänderung in "x-Richtung"
    4. Die allgemeine Sinuskurve - Graphen zuordnen und zeichnen
    5. Bestimmung der Funktionsgleichung einer allgemeinen Sinusfunktion
  4. Modellierung mit Hilfe der Sinusfunktion
    1. Modellierung einer Trigonometrischen Funktion (Sonnenverlauf)

1.

3.1 Sinus und Kosinus am Einheitskreis (Wiederholung)

  • 1. Trigonometrie im rechtwinkligen Dreieck und am Einheitskreis
  • 2. Sinus, Kosinus, Tangens am Einheitskreis
  • 3. Wiederholung: Funktion und ihre Darstellungen

1.1.

Trigonometrie im rechtwinkligen Dreieck und am Einheitskreis

Hier siehst du einen Einheitskreis. Überlege, wie Sinus und Kosinus mit den Koordinaten des Punktes P zusammenhängen.
Aufgaben
Hast du die Ankathete zum Winkel [math]\alpha[/math] schon entdeckt? Wo sind hier die Gegenkathete und die Hypotenuse?
Warum ist dieser Kreis ein Einheitskreis?
Der Punkt P liegt auf der Kreislinie. Gleichzeitig wird mithilfe von P ein rechtwinkeliges Dreieck aufgespannt - Hast du den rechten Winkel gefunden?[br]Nun kannst du vielleicht schon einen Zusammenhang erkennen:[br]Cos([math]\alpha[/math]) ist genau...
Hier siehst du einen Einheitskreis. Überlege, wie Sinus und Kosinus mit den Koordinaten des Punktes P zusammenhängen.
Erster Quadrant
Für 0°<[math]\alpha[/math]<90° gilt: Je größer [math]\alpha[/math], desto...
Im allgemeinen Dreieck wird der Sinus berechnet durch ...
– Regina Paleczek, Veronikar510

1.2.

–

1.3.

–

2.

3.2 Vom Einheitskreis zur Sinuskfunktion

  • 1. Sinus am Riesenrad
  • 2. Die Entstehung der Sinus- und Kosinusfunktion aus dem Einheitskreis

2.1.

Sinus am Riesenrad

Frage 1:
Findest du eine Gemeinsamkeit des Riesenrades mit den vorherigen Kapiteln? Beschreibe!
Auftrag: Arbeite mit dem nachfolgendem Riesenrad
Überlege, wie der Graph der einer Funktion f(x)=sin(x), die jedem Winkel x den Wert sin(x) zuordnet, aussehen könnte. [br]Verwende erst nach längerem Überlegen und Betrachten der Gondeln die Hilfslinien und lasse dir dann zuletzt den Graphen anzeigen.
Sinus am Riesenrad
Auftrag: Bearbeite die Vorderseite des Arbeitsblattes "Riesenrad"
– Regina Paleczek, Walter Senzenberger

2.2.

–

3.

3.3 Die allgemeine Sinusfunktion

  • 1. Wiederholung: Manipulationen von Funktionen
  • 2. Form und Lageänderung in "y-Richtung"
  • 3. Form und Lageänderung in "x-Richtung"
  • 4. Die allgemeine Sinuskurve - Graphen zuordnen und zeichnen
  • 5. Bestimmung der Funktionsgleichung einer allgemeinen Sinusfunktion

3.1.

Wiederholung: Manipulationen von Funktionen

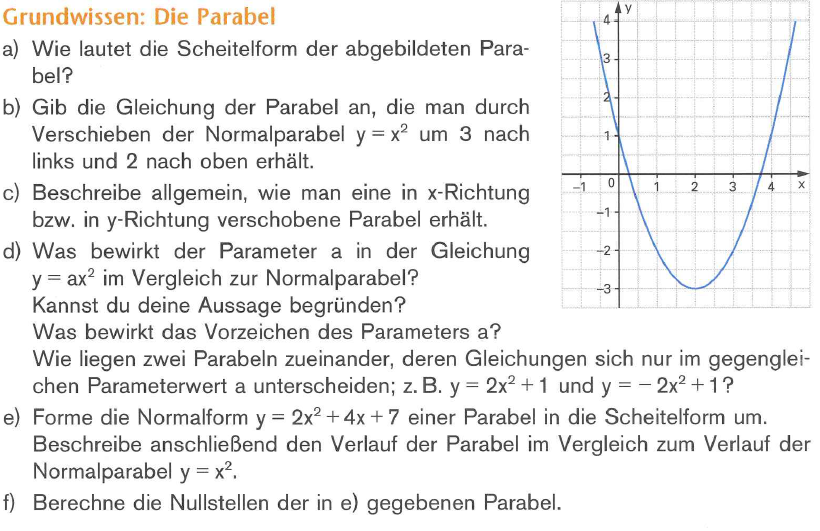
Quelle: Mathematik 10, BSV, S.54
Antwort a:
Antwort b:
Antwort c:
Antwort(en) d:
Freiwillig: Hilfestellung zur Bearbeitung von Aufgabe e
Antwort e:
– Regina Paleczek

3.2.

–

3.3.

–

3.4.

–

3.5.

–

4.

Modellierung mit Hilfe der Sinusfunktion

  • 1. Modellierung einer Trigonometrischen Funktion (Sonnenverlauf)

4.1.

Modellierung einer Trigonometrischen Funktion (Sonnenverlauf)

Hier siehst Du eine Fotoserie von der Mitternachtssonne, fotografiert vom Nordkapp aus. Da die Kamera im Stundenabstand die Einzelbilder aufgenommen hat, musste der Fotograph das Kamerastativ entsprechend weiter drehen. Nach der Aufnahmenserie wurden Streifen der Einzelbilder so aneinander gereiht, dass ein Panorama-Zeit-Foto entstanden ist. Das Koordinatensystem ist willkürlich, es könnte z.B. in die Kameralinse eingeblendet worden sein.[br][br]Modelliere nun den Graphen der Sinusfunktion so, dass sie in diesem willkürlichen Koordinatensystem den jeweiligen Sonnenstand zur richtigen Zeit beschreibt. Dazu kannst Du mit Hilfe der Regler jeden der vier Parameter a ("Amplitude"), b ("Frequenz"), c ("Verschiebung") sowie d ("y-Achsenabschnitt") verändern.[br][br]Lege also eine passende Kurve durch die jeweiligen Sonnenmittelpunkte"!
Welche Periodenlänge hat die modellierte Funktion ungefähr?
– Regina Paleczek, Thomas Bay, Matthias Hornof

Information