Francis Galton (1822-1911)
Stochastik
In dieser Lerneinheit werden verschiedenste Themen der Stochastik behandelt und visualisiert.
Table of Contents
- Galtonbrett
- Galtonbrett
- Binomialverteilung
- Histogramm
- Kumulierte Wahrscheinlichkeit
- Zusammenfassung
Galtonbrett
[size=85]Zur Demonstration und Veranschaulichung der [b]Binomialverteilung[/b] entwickelte Sir[b] Francis C. Galton[/b] (1822-1911) eine Anordnung, die man als [b]Galton-Brett[/b] bezeichnet. [br][br]Auf einem "realen" Brett sind mehrere Nägel befestigt, die wie gleichmäßige Dreiecke angeordnet sind und zusammen ein gleichseitiges Dreieck bilden. Die Anordnung entspricht einem Pascalschen Dreieck.[/size]
[size=85][b]Mache dir Notizen zu folgenden Fragestellungen:[/b][br][br](1) Wie gelangt eine Kugel überhaupt in ein bestimmtes Fach?[br][br](2) In welchem Topf erwartest du die meisten Kugeln, wenn p = 0,5? Warum?[br][br](3) Was bedeutet eine Veränderung von p?[br][br](4) Was ändert sich, wenn man das Brett etwas zur Seite kippt?[br][br](5) Stope die Animation nach 100 Versuchen und skizziere ein vereinfachtes Galtonbrett und [br] übertrage darunter das Balkendiagramm und die Tabelle in dein Heft.[br][br](5) Versuche eine allgemeine Formel aufzustellen, die die Wahrscheinlichkeitsverteilung bei einem [br] symmetrischen und bei einem unsymmetrischen (zur Seite gekippten) Galtonbrett berechnet.[br][br](6) Überlege dir Zufallsexperimente, die mit dem Galton[/size]brett veranschaulicht werden können.
Reales Galtonbrett[br]
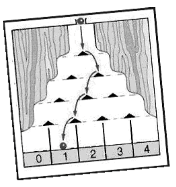
Unsymmetrisches Galtonbrett[br]
Histogramm
Mit der Formel von Bernoulli lassen sich die Wahrscheinlichkeiten der einzelnen Trefferanzahlen berechnen, sodass jeder Trefferanzahl k ihre Wahrscheinlichkeit P(X=k) zugeordnet wird. [br][br]Die Funktion, die jeder Zahl k die Wahrscheinlichkeit B[sub]n;p[/sub](k) zuordnet, heißt [b]Bionomialverteilung[/b] mit den [b]Parametern n und p[/b]. Man sagt: Die Zufallsgröße X ist [b]B[sub]n;p[/sub](k)-verteilt.[br][/b][br]Diese Verteilung kann man grafisch in einem [b]Histogramm[/b] darstellen. [br]Ein Histogramm ist ein Säulendiagramm, bei dem die Wahrscheinlichkeiten P(X=k) durch die Flächeninhalte der Rechtecke veranschaulicht werden.[br]Bei der Bernoulli-Kette ist die Breite eine Säule immer eins, sodass auch die Höhen der Säulen den Wahrscheinlichkeiten P(X=k) entsprechen.
[b]Bearbeite folgende Aufgaben:[/b][br][br][u]Aufgabe 1:[/u][br]Verändere die einzelnen Schieberegler. Was haben die verschiedenen Parameter für Auswirkungen?[br][br][u]Aufgabe 2:[/u][br]Gebe die Wahrscheinlichkeitsverteilung der binomialverteilten Zufallsgröße mit den Parametern n und p an und zeichne das Histogramm in dein Heft. [br]Markiere jeweils den k-ten Treffer, bei dem die höchste Trefferwahrscheinlichkeit erwartet wird. [br](a) n = 3 p = 0,4[br](b) n = 100 p = 0,5