fasci di rette
Inhaltsverzeichnis
- fascio proprio di rette
- Fascio di rette proprio
- fascio improprio di rette
- Copia di Fascio improprio di rette
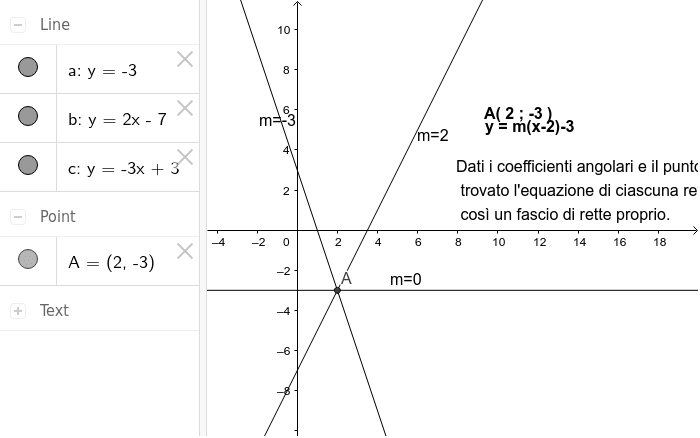
Fascio di rette proprio
Il fascio di rette proprio è l'insieme di tutte le rette che passano per un punto, detto centro del fascio.[br]Nell'equazione del fascio proprio il coefficiente angolare, cioè la pendenza della retta può variare.[br]L'equazione del fascio proprio di rette, si ottiene dalla formula:[br][math]y-y_0=m\left(x-x_0\right)[/math][br]Questa equazione descrive tutte le rette che passano per il punto di coordinate (x ; y), per qualsiasi valore che assume m. Però non rappresenta la retta parallela all'asse dell'ordinate, che ha come equazione x=x0[br]
Copia di Fascio improprio di rette
Con questa costruzione si vuole descrivere una delle possibili posizioni che due o più rette possono assumere reciprocamente. [br]Utilizzando lo slider si varia il valore di "q", quota o ordinata all'origine dell'equazione lineare, e si ottengono tutte le infinite rette parallele alla retta [i]f[/i] assegnata (in rosso). L'insieme di queste infinite rette parallele tra loro viene definito Fascio Improprio di rette. [br]In questo modo si può ossevare che:[br]- il coefficiente angolare "m" rimane uguale, quindi le rette hanno tutte la stessa pendenza e formano angoli uguali rispetto all'asse x;[br]- le rette non hanno punti comuni, per questo motivo si dicono PARALLELE DISTINTE;[br]