Lagebeziehung Punkt-Gerade
Ermittlung, ob ein Punkt P auf einer Geraden liegt
[size=100][u]1. Die Gerade r liegt in der allgemeinen Form ax+by=c vor.[/u][/size][br][br][b]Vorgehensweise[/b]: Koordinaten des Punktes P in die Geradengleichung einsetzen und prüfen, ob die Gleichung gelöst wird.[br][br][b]Beispiel[/b]: P(1;2) und r: x+2y=-1[br][br][b]Lösung[/b]: der Punkt liegt nicht auf der Geraden. Denn setzt man die Koordinaten des Punktes in die Geradengleichung links ein, erhält man[br][math]1+2\cdot2=5\ne-1[/math][br][br][u]2. Die Gerade r liegt in Parameterform vor[/u].[br][br][b]Vorgehensweise:[/b] Ersetze in der Parameterform der Geraden r die Punktkoordinaten durch jene des Punktes P. Der Punkt liegt auf der Geraden, wenn der Wert des Spurparameters für jede Koordinatengleichung übereinstimmt[br][br][b]Beispiel[/b]: P(9;6) und r:[math]\binom{x}{y}=\binom{-1}{4}+t\binom{5}{1}[/math][br]Lösung: Ersetze in der Geradengleichung x und y durch die Werte von P[br][math]9=-1+t5[br][/math] <=> t=2[br][math]6=4+t[/math] <=> t=2[br]Die Lösungswerte stimmen überein. P liegt auf der Geraden
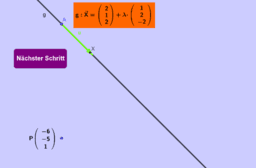
Liegt der Punkt P auf der Geraden r?
P(5;-3) und r:[math]\binom{x}{y}=\binom{-4}{3}+t\binom{-6}{4}[/math]
Liegt der Punkt P auf der Geraden r?
P(4;-3) und r: -3x+2y=6
Besondere Punkte und Linien in Dreiecken mit Vektoren erfassen
a) Welche besonderen Linien und Punkte haben wir kennen gelernt?
In einem Dreieck kannst du verschiedene besondere Linien einzeichnen, die eine Bedeutung für die Eigenschaften des Dreiecks haben. Dieses Arbeitsblatt gibt dir einen Überblick.
Übersicht über besondere Linien und Punkte im Dreieck
Weißt du das noch?
Der Schwerpunkt von einem linearen Segment durch Punkte A und B wird vektoriell erfasst durch
Schwerpunkt im Dreieck
Der Schwerpunkt in einem Dreieck mit Eckpunkten A,B,C wird vektoriell erfasst durch
Der Umkreismittelpunkt und Umkreisradius
Wie du oben gesehen hast, ist der Umkreismittelpunkt [math]M_U[/math] der Schnittpunkt der Mittelsenkrechten [math]m_a[/math] , [math]m_b[/math] und [math]m_c[/math].[br][b][color=#0000ff]Vorgehensweise[/color][/b]: [br][i]a) Bilde die Richtungsvektoren AB, BC und AC (es reichen im Prinzip zwei Vektoren)[br]b) Ermittle die Mittelpunkte [math]M_a,M_b,M_c[/math] (Schwerpunkte) der Seiten a,b,c (es reichen zwei)[br]b) Ermittle aus den Richtungsvektoren durch Drehung die Normalenvektoren zu den Seiten a,b,c (es reichen zwei)[br]c) Ermittle die Parameterformen der Mittelsenkrechtengeraden[br]d) Ermittle den Schnittpunkt [math]M_U[/math] der Geraden durch Gleichsetzen der Parameterformen[br][/i][br][b][color=#0000ff]Alternativ[/color][/b]: Ermittle die allgemeine Geradengleichungen aus der Normalenvektorgleichung für die Mittelsenkrechten. Dazu benötigt: Die Richtungsvektoren für zwei Seiten z.B. a und c und die zugehörigen Mittelpunkte[br][br][b][color=#0000ff]Umkreisradius[/color][/b]: Berechne den Betrag eines Verbindungsvektors zwischen dem Mittelpunkt und einem Eckpunkt des Dreieck
Jetzt du!
Ermittle den Umkreismittelpunkt zum Dreieck mit Eckpunkten A(-2;0), B(0;3) und C(3;1)
Der Inkreismittelpunkt
Der Inkreismittelpunkt M_I ist der Schnittpunkt der Winkelhalbierenden des Dreiecks. Er kann durch eine einfache Formel erfasst werden.[br][br][b][color=#0000ff]Formel[/color][/b]: M_I = (aA+bB+cC)/(a+b+c)[br][br]Der [b][color=#0000ff]Inkreisradius[/color][/b] r_I ist der [b][color=#0000ff]Normalenabstand[/color][/b] des Punktes M_I zu den Seiten a,b,c[br][br][color=#0000ff][b]Idee zur Herleitung:[/b][/color][br]Die Winkelhalbierenden können wie folgt erfasst werden:[br]Winkelhalbierende durch den Eckpunkt A: der Richtungsvektor w_A ist die Vektorsumme [br]w_A=bAB+cAC [br][br][b][color=#0000ff]Erläuterung[/color][/b]: die Verbindungsvektoren von A zu B und C werden so skaliert, dass sie die gleiche Länge besitzen. Die Vektorsumme von zwei gleich langen Vektoren ist ein Vektor, der den Winkel der beiden Vektoren halbiert.[br][br]Ermittelt man nun den Schnittpunkt der Winkelhalbierenden w_A, w_B , w_C erhält man mit etwas Rechnung die obige Formel.[br][br][b][color=#0000ff]Challenge[/color][/b]: leite die obige Formel her!
Jetzt du!
Ermittle zum obigen Dreieck rechnerisch den Inkreismittelpunkt und den Inkreisradius
Lagebeziehungen von Geraden
Einleitung
Mit Hilfe dieser Seite untersuchen wir die verschiedenen Lagebeziehungen zweier Geraden im Raum.[br][br]Die meisten Aufgaben sind mit Hilfe der Applets zu lösen. Manche jedoch auch ohne.[br]In jedem Fall werden Notizen benötigt, damit wir die Lösungen gut vergleichen können.[br]-------------------------------------------------------------------------------------------------------
Vorbereitung
[b][color=#0000ff]Nimm dir 2 Stifte und stelle zunächst selbst verschiedene Lagebeziehungen zwischen zwei Geraden dar.[br]Beschreibe und notiere die Lagebeziehungen möglichst genau.[/color][/b][br][br]-------------------------------------------------------------------------------------------------------[br]
Möglichkeit 1
a) Mache dich mit den Schiebereglern vertraut. Welchen Teil der Gerade verändern sie?[br][br]b) Welche Gemeinsamkeiten und Unterschiede müssen g und h haben, sodass diese Lagebeziehung entsteht?[br][br]c) Es gibt hier einen Sonderfall. Finde ihn.
Applet zu Möglichkeit 1
Möglichkeit 2
a) Mache dich mit den Schiebereglern vertraut. Welchen Teil der Gerade verändern sie?[br][br]b) Welche Gemeinsamkeiten und Unterschiede müssen g und h haben, damit diese Lagebeziehung entsteht?[br][br]c) Es gibt hier einen Sonderfall. Finde ihn.
Applet zu Möglichkeit 2
Möglichkeit 3
a) Bewege die Ansicht, sodass du die Geraden aus verschiedenen Blickwinkeln betrachten kannst.[br][br]b) Wie unterscheidet sich diese Lage von den vorherigen?[br][br]c) Welche Gemeinsamkeiten und Unterschiede müssen g und h haben, sodass diese Lagebeziehung entsteht?[br][br]d) Ist diese Lagebeziehung auch im 2-Dimensionalen möglich? Begründe deine Antwort.
Applet zu Möglichkeit 3
Rechnerische Bestimmung der Lage von zwei Geraden in Parameterform
1. Überprüfe zuerst, ob die Richtungsvektoren kollinear sind[br][br](Wie geht das nochmal? zwei Vektoren [math]\binom{a}{b}[/math] und [math]\binom{c}{d}[/math] sind kollinear, wenn ihre Komponenten komponentweise[br][list][*]gleich Null sind (z.B. a=c=0) ODER[/*][*]die Verhältnisse der Komponenten gleich sind a:c = b:c )[/*][/list][br]Daraus ergeben sich [b][color=#0000ff]zwei Alternativen[/color][/b][br][br][table][tr][td]Richtungsvektoren sind [b]nicht kollinear:[/b][/td][td][/td][td]Richtungsvektoren sind [b]kollinear[/b]:[/td][/tr][tr][td]In der Ebene: Geraden müssen sich [b]schneiden[/b][br]Im Raum: Geraden schneiden sich [br]ODER [br]sind [b]windschief[/b] [br][br][/td][td][/td][td]Geraden sind [b]parallel[/b][br]ODER[br]Geraden sind [b]identisch[/b][/td][/tr][/table][br][br]2. Um die Lagebeziehung eindeutig zu klären, muss eine Probe durchgeführt werden:[br]Setze die Parameterformen gleich und bestimme die Lösungsmenge[br]r_1: [math]\binom{x}{y}=\binom{a}{b}+t\binom{v_x}{v_y}[/math] Spurparameter t[br]r_2: [math]\binom{x}{y}=\binom{c}{d}+s\binom{w_x}{w_y}[/math] Spurparameter s[br]Setze die rechten Seiten gleich und löse nach t und s (Lineares Gleichungssystem)[br][br][math]\left(I\right)a+tv_x=c+sw_x[/math][br][math]\left(II\right)b+tv_y=d+sw_y[/math][br][br]Es ergeben sich [b]zwei Fälle:[/b][br]1) Nicht-kollineare Richtungsvektoren[br][br][table][tr][td]Lösungsmenge eindeutig =>[/td][td]Geraden schneiden sich in einem Punkt[/td][/tr][tr][td]Lösungsmenge ist leer =>[/td][td]Geraden sind windschief[/td][/tr][/table][br]2) kollineare Richtungsvektoren[br][table][tr][td]Lösungsmenge leer =>[/td][td]Geraden sind parallel[/td][/tr][tr][td]Lösungsmenge allgemein (unendlich viele Lösungen) =>[/td][td]Geraden sind identisch[/td][/tr][/table][br]Im Falle kollinearer Richtungsvektoren kann auch verkürzt eine Punktprobe durchgeführt werden (Aufpunkt in die Parameterform einsetzen und prüfen, ob der Aufpunkt auf der anderen Geraden liegt)[br]
Probiere es nun selbst aus
1) In welcher Beziehung sind die Geraden r_1: [math]\binom{x}{y}=\binom{1}{2}+t\binom{3}{6}[/math] und r_2[math]\binom{x}{y}=\binom{3}{0}+s\binom{-1}{-2}[/math]
2) Zeige, dass die Geraden r_1: [math]\binom{x}{y}=\binom{2}{3}+t\binom{5}{2}[/math] und r_2: [math]\binom{x}{y}=\binom{4}{0}+s\binom{0}{3}[/math] sich schneiden und bestimme den Schnittpunkt[br]